核心素養背景下初中數學項目式學習

上海市盧灣中學 李 佼

《義務教育數學課程標準（2022年版）》指出，初中階段的核心素養主要表現為：抽象能力、運算能力、幾何直觀、空間觀念、推理能力、數據觀念、模型觀念、應用意識、創新意識。夏雪梅教授在《項目化學習設計：學習素養視角下的國際與本土實踐》中提出六維度項目化學習框架：①核心知識；②驅動性問題；③高階認識；④學習實踐；⑤公開成果；⑥全程評價。此框架為開展項目學習提供了設計模板，通過項目學習，建立起學科知識與真實世界之間的聯系，培養學生核心素養。

滬教版七年級下冊第十五章“平面直角坐標系”是數形結合的平臺，是學生學習函數圖像和平面解析幾何的必要基礎。平面直角坐標系的建立，是數軸概念的發展和理性思維的成果，同時又有現實生活經驗的基礎。對平面直角坐標系的學習，學生不僅需要理解其相關知識，還需要體會平面直角坐標系與實際生活的聯系，能從實際情境中抽象出數學概念，建立模型，用數形結合的思想方法來解決相應問題。基于此，筆者積極探索如何通過項目學習，幫助學生理解數學與生活的聯系，培養其抽象能力、模型觀念、應用意識、創新意識等核心素養。

一、項目開發背景

五子棋游戲起源于中國古代的傳統黑白棋種之一，它簡單易學、趣味無窮，是一種兩人對弈的純策略型棋類游戲。滬教版七年級下冊第十五章“平面直角坐標系”的探究活動二提出的就是五子棋的相關內容。教材中，通過一種新的棋譜記法，學生可以將生活中的實際問題數學化，用數學語言來描述棋子的位置。在此基礎上，筆者發現五子棋棋譜是網格式的，與平面直角坐標系類似，棋手在訓練過程中，記錄棋子的方式是通過橫向的阿拉伯數字和縱向的英文字母組合而成，這與平面直角坐標系中點的表示方法類似，由此可抽象出與平面直角坐標系的關系，建立數學模型。因此，筆者決定以五子棋游戲為背景，聯系平面直角坐標系的知識，結合其他對弈游戲的規則，讓學生從玩者變成設計者，加入數學元素重新設計五子棋游戲規則，“巧玩五子棋”這個項目也就應運而生。

二、項目設計

在項目設計之初，我們先整理了平面直角坐標系的相關知識點（如圖1），確立了知識發展序列。基于知識發展序列，設計與之相匹配的項目任務線。在北京師范大學專家團隊的指導下，經過幾次修改完善，我們確定了項目的驅動性問題和本質問題，對整個項目的內容進行了設計。

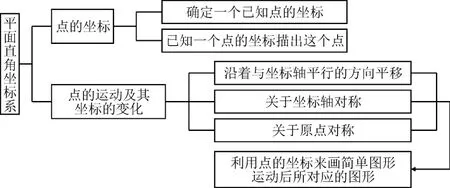
圖1 “平面直角坐標系”知識結構圖

（一）項目任務

項目的具體實施需要明確的任務規劃。在本項目的本質問題（五子棋游戲的新規則設計）的驅動下，我們設計了三個任務來推進整個項目的進行。任務1是“設計新的棋譜記法”，這是新規則設計的基礎，承載的知識點是“有序實數對”及“平面直角坐標系的概念”；任務2是“五子棋新規則的基礎版”，這是在常規規則的基礎上增加一點難度，比如，說出棋子的坐標等，承載的知識點是“用坐標表示平面內的點”“垂直于坐標軸上的直線的表示方法及平行于坐標軸的直線上的兩點的距離”；任務3是“五子棋新規則的進階版”，任務2中棋盤上的棋子是不動的，但在任務3中，棋盤上的棋子可以像象棋一樣進行移動，這也是形成完整的設計方案的最終任務，承載的知識點是“直角坐標系中的平移、軸對稱、中心對稱”。

（二）問題序列與知識發展

按照“以任務推進為明線，以知識發展為暗線”的原則，在三個項目任務的驅動下，我們對每個任務設置了問題序列，合理地將相關數學知識承載于各個問題中（如表1）。整個設計通過問題鏈的形式將項目的任務線與數學知識同時推進，兩者之間相互融合，不僅形成項目的最終成果，也落實相關的數學知識，培養了學生的學科素養。

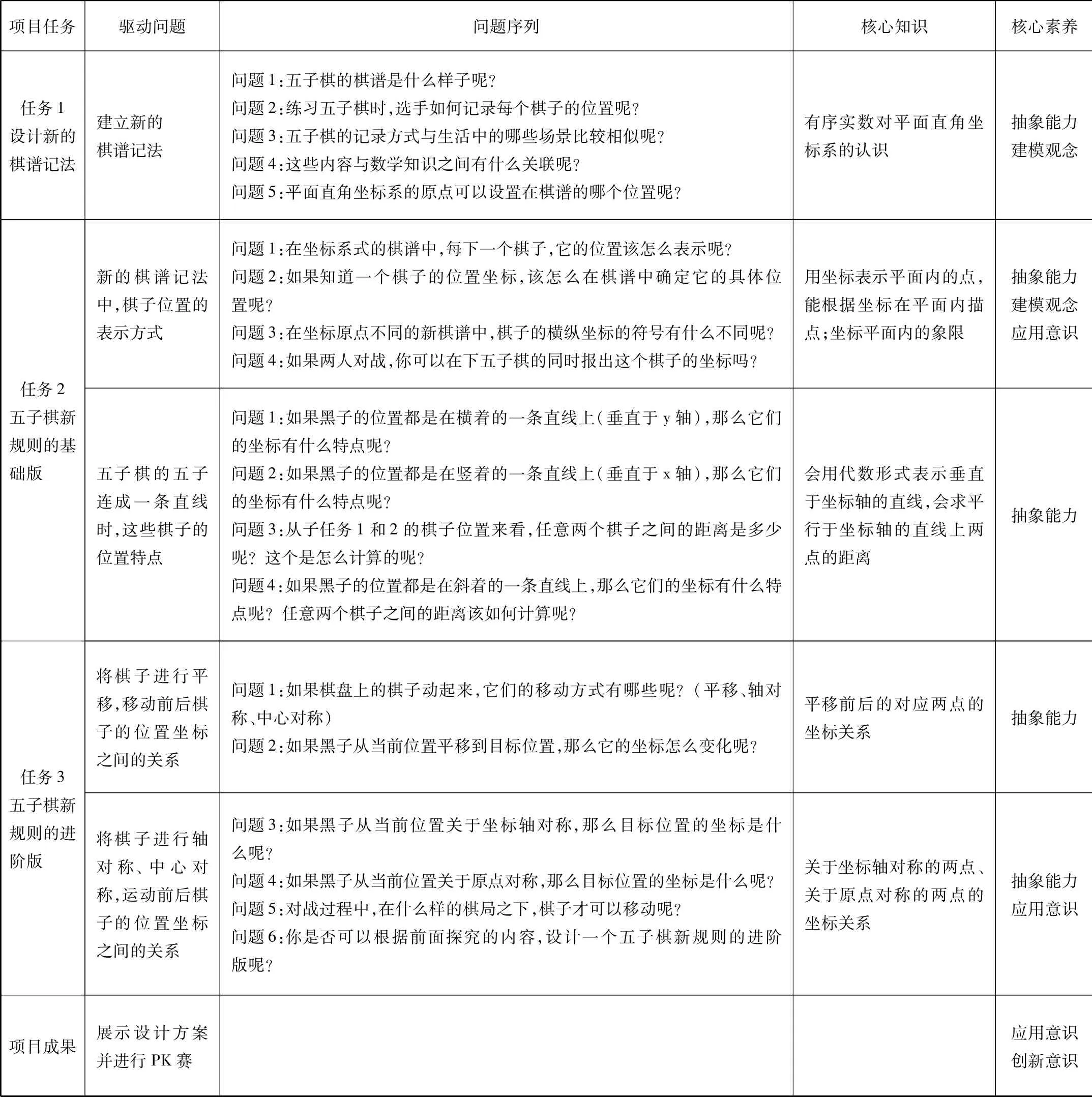
表1 “巧玩五子棋”項目設計框架

三、項目實施

針對整個項目的實施，筆者主要介紹最后展示課的實施過程。最后的展示課分為四個環節：整理回顧、成果展示、小組PK賽、總結評價。

第一，整理回顧。在之前的學習中，學生對整個項目的背景、任務及所學的數學知識十分了解，但學生關注更多的是局部知識的學習和應用，通過回顧整理，學生對項目的整體有了新的認識，能從整體的角度去理解整個項目的學習。

第二，成果展示。這個環節主要是每個小組展示分享五子棋新規則的設計方案，其他小組根據他們分享的情況進行提問，給出評價，在所有小組展示結束后，評選出最佳方案。評價的要素包括學科知識的使用，規則設計的合理性、創新性等，以及語言表達能力情況。通過提問、回答，學生可以跳出自己的思維，重新審視設計的規則，有助于之后的修改、完善。經過展示，學生語言表達能力有所提高，也體會了團隊合作的重要性。

第三，小組PK賽。此環節的具體設置如下：PK賽的裁判和相關工作人員是最佳方案小組成員，具體的五子棋規則按照他們的設計方案來進行，其他小組進行抽簽決定PK對象，完成整個PK賽。這個環節的巧妙之處在于五子棋規則的選擇，獲得最佳方案的設計也可以通過實踐來驗證它們的合理性、可行性，不僅使比賽公平公正，也讓他們意識到理論與實踐相結合的重要性。

第四，評價總結。具體分為學生總結和教師總結。學生可以對自己在整個項目的所學所得進行總結，也可以對自己的整個學習過程做自我評價。教師對整個項目的開展實施和學生在整個項目中遇到的問題以及如何解決問題等進行總結。

課后作業是針對在展示交流中，大家對設計方案提出的問題進行進一步的修改完善，形成最終的成果。

四、項目反思

基于教材單元內容，此項目從探究活動出發，以真實情境為切入點設計驅動性問題，通過解決問題，形成與實際生活相關的項目成果。整個過程中以項目任務為明線，數學知識為暗線，雙線逐步推進，相互融合，學生在“玩”中學，學中“玩”，體會到數學知識在實際生活中的運用，感受到數學來源于生活又服務于生活。

（一）對項目設計的反思

在具體實施過程中，整個設計和課堂呈現還有一定的不足之處。北京師范大學的專家團隊也對整個教學設計進行了多次指導，其中吉林師范大學的郝連明副教授提出展示課中的整理回顧可以放在最后的總結評價中進行，展示之后再整體總結，效果會更好；展示過程中，對作品的要求可以指向更為具體的數學知識；評價內容可以進一步關注非認知因素。

（二）自身成長

通過這次項目開發和實施，筆者明確了項目背景需要簡單扼要，通過引入話題，指明方向，引起學生的興趣，告訴學生“這個項目將要干什么”；在確定項目目標時，需要將項目任務與數學知識聯系起來，突出做中學，一般項目目標只需要三四個即可；在進行具體的教學設計時，需要將任務線和數學知識相互融合，在推進項目任務的同時掌握相應的數學知識。

（三）后續學習

項目式學習是學生學習的過程，也是加強學生綜合與實踐能力的一種重要的學習方式。項目式學習以用數學方法解決現實問題為主，引導學生發現、解決現實問題，用數學的思維分析要素之間的關系，培養模型觀念，培養應用意識和創新意識。對之后的項目開發，除了參考教材上的探究活動外，也可以多留心生活中的實際問題、社會熱點問題，多思考這些問題與數學知識的聯系，挖掘適合現階段學生的知識點，讓學生可以在真實情境中用適切的數學語言表達相關問題，解決問題，形成實際有效的項目成果。

（四）項目延續性

雖然這個項目是在七年級進行的，但這個項目還具有延續性。在七年級，要求掌握平行于坐標軸的兩點的距離公式，而棋盤上任意兩點之間的距離涉及的知識是八年級的勾股定理和兩點間的距離公式；在七年級，要求掌握垂直于坐標軸的直線的代數表示形式，但若五子斜著連成一條直線，這條直線的代數表示形式涉及的是八年級的一次函數的內容，所以這個項目在八年級也可以進行。同時，學生玩五子棋游戲的水平高低，派哪位成員代表小組出賽等，這些內容涉及的是九年級的統計初步，所以在學習這些數學知識時，也可以考慮五子棋項目。這個項目在后續還有很多可開發的點，需要我們繼續努力，認真研究。