基于FSK-PSK復合調制的正交波形設計

杜 盈， 張勁東， 蔣宜林, 尹明月

(南京航空航天大學電子信息工程學院， 江蘇南京 211100)

0 引言

欺騙性干擾是指干擾機將截獲到的信號經過部分復制后轉發給雷達，使得對方雷達跟蹤到虛假目標，從而保護真實目標，同時雷達系統還可能因為要處理的假目標太多而無法正常工作。現代雷達可通過發射正交波形來降低各子脈沖之間的互相關性，同時利用信號的隨機性和不確定性使干擾信號脈壓后的輸出盡可能小，從而降低信號的截獲概率，以此來抑制欺騙干擾。此外，多輸入多輸出(Multiple-Input Multiple-Output, MIMO)雷達也要求發射正交波形，因此對正交波形的優化設計具有重要意義。

常用的正交波形形式是相位編碼信號。文獻[1-5]以自相關旁瓣最大值、互相關最大值、自相關旁瓣能量和互相關能量等的加權和為目標函數，設計具有良好正交性能的相位編碼；文獻[6]和[7]則以自相關和互相關函數的峰值旁瓣電平比(Peak Sidelobe Level Ratio, PSLR)以及積分旁瓣電平比(Integrated Sidelobe Level Ratio, ISLR)構建代價函數優化多相正交序列。但隨著現代雷達技術的不斷發展，單一的調制信號形式已不能滿足現代信息化戰爭的新要求，從脈內、脈間多個維度設計復合調制波形可以提高信號的隨機性和復雜度，從而降低雷達的截獲概率，提升雷達的抗干擾能力。FSK-PSK信號就是一種常見的復合調制信號形式。唐璐對跳頻信號進行相位調制得到具有良好的隨機性和低截獲特性的FSK-PSK復合調制信號，Chang等設計了比傳統離散頻率編碼波形具有更好的正交性和更低的旁瓣的離散頻率/相位編碼波形(Discrete Frequency and Phase Coding Waveform, DFPCW)，張洋通過優化信號捷變頻率和脈內相位編碼分別改善了信號的多普勒旁瓣水平和距離旁瓣水平，但這些文獻并沒有對欺騙干擾的抑制展開研究。

本文在以上研究的基礎上，以脈內切片轉發干擾(Intrapulse Slice Repeater Jamming , ISRJ)為例，設計脈內相位編碼、脈間跳頻編碼的FSK-PSK正交波形來對抗壓制干擾，以最小化子脈沖的自相關旁瓣電平和各個子脈沖之間的互相關函數電平加權和為準則，用0-1離散變量表示跳頻和相位，將原優化問題轉化為0-1整數規劃問題，構造增廣拉格朗日函數，對所有0-1變量求導，采用擬牛頓法求解優化問題模型，從而對FSK-PSK復合調制信號的跳頻和相位進行聯合優化。

1 信號形式和優化問題模型

1.1 FSK-PSK復合調制下的ISRJ

將一個脈寬為的寬脈沖分為個彼此相接的子脈沖，每個子脈沖的脈寬=，采用跳頻編碼序列對子脈沖進行調制。每個子脈沖中用長度為的相位編碼序列進行調制，每個碼元的寬度=,為了提高信號的隨機性和復雜度，每個子脈沖的相位編碼序列均不相同。FSK-PSK復合調制信號模型如圖1所示。

圖1 FSK-PSK復合調制信號模型

那么信號的復包絡可寫為如下形式：

(1)

式中，()表示第個子脈沖信號：

(2)

其中，=,=1,2,…,為頻點，∈[1,2,…,]為第個子脈沖的跳頻系數，本文假設每個子脈沖的跳頻系數均不相同；()=ej2π()，=0,1,…,-1表示第個子脈沖的相位編碼序列，()∈[0,1,…,-1]為相位離散值，表示離散相位個數，()為寬度的理想矩形脈沖。

脈內切片轉發干擾即部分脈沖轉發干擾，是指干擾機對截獲到的雷達發射信號按照預先設定的次數進行采樣并轉發形成的干擾，是一種典型的欺騙干擾形式，采樣周期和采樣時長的不同決定了不同的干擾形式。脈內切片轉發干擾比脈間轉發干擾的功率利用率更高，干擾形式也更加多樣。

假設干擾機對所截獲的FSK-PSK復合調制信號，在一個碼元內采樣點，即以=為周期進行采樣(切片)，隨后將切片信號轉發出去，形成脈內切片干擾信號，其信號形式如圖2所示。

圖2 ISRJ信號模型(第m個子脈沖)

那么整個脈沖共采樣′=·個點，采樣后的第個子脈沖信號可表示為

(3)

1.2 優化問題模型

利用式(3)計算第個子脈沖和第個子脈沖的互相關：

(4)

取=,-(′-1)≤≤′-1有

(5)

將()簡寫為()，并定義：

,=·,··

那么第個子脈沖和第個子脈沖的互相關函數的離散形式可表示為

(6)

當=時，式(6)表示第個子脈沖的自相關函數的離散形式：

(7)

為對抗ISRJ信號，可設計FSK-PSK脈內正交波形，以最小化子脈沖的自相關旁瓣電平和各個子脈沖之間的互相關函數電平加權和為準則建立目標函數，優化FSK-PSK復合調制信號。該問題的目標函數可表示為

(8)

式中，=[|≤||≤′-1]表示自相關的副瓣范圍，=[|0≤||≤′-1]表示互相關函數范圍；∈[0,1]為加權系數，當=1時，只抑制自相關函數副瓣部分即，而=0時，只抑制互相關函數電平部分即。

考慮跳頻系數和相位部分離散值()的整數約束以及各子脈沖跳頻系數兩兩不同的約束條件，可建立如下優化問題模型：

(9)

2 抗ISRJ的FSK-PSK正交波形優化方法

2.1 0-1整數規劃模型

對于0-1離散變量，需要利用如下光滑處理的NCP(Nonlinear Complementarity Problem)函數，將其轉化成為連續問題：

(10)

式中為極小的正數。問題可改寫為如下形式：

(11)

式中第一項約束條件是對跳頻系數的整數約束，共個，第二項約束條件是對相位部分離散值的整數約束，共個，第三項約束條件是關于0-1離散變量的NCP函數，共(+)個，第四個約束條件表示各子脈沖跳頻系數兩兩不同，共個。將所有約束條件進行如下描述：

()=0,=1,2,…，

=++(+)+

(12)

通過增廣拉格朗日乘子法將該優化問題轉化為無約束優化問題可得

(13)

式中=[,,…,]為拉格朗日乘子組成的向量，=[,,…,]為懲罰因子組成的向量。采用擬牛頓法求解無約束優化問題得到：=argmin(,,)。這一方法需要對變量求導。

首先對目標函數表達式(8)作如下轉換：

(14)

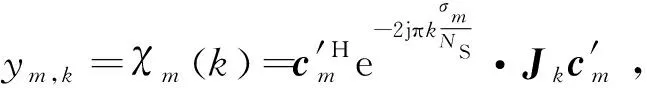
2.2 優化跳頻

2.2.1 目標函數求導

對于自相關函數()，根據求導鏈式法則得

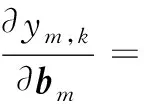
(15)

對于互相關函數()：

(16)

求式(16)中各項：

(17)

那么函數()、()分別對跳頻部分變量求導得

(18)

則目標函數對跳頻部分求導得

(19)

2.2.2 約束條件求導

約束條件對變量(1≤≤,=1,2,…,)求導，此時∈。

(20)

式中=(+1)+(-1)(+)。

2.3 優化相位

2.3.1 目標函數求導

自相關函數對相位部分求導：

(21)

計算式(21)中各項：

1,…,-1)]

(22)

將式(22)代入式(21)并化簡可得

(23)

互相關函數對相位部分變量求導得

(24)

根據式(22)可求式(24)并化簡：

(25)

那么函數()、()分別對相位部分變量求導得

(26)

則目標函數對相位部分變量求導得

(27)

2.3.2 約束條件求導

約束條件對變量(+1≤≤+,=1,2,…,-1)求導，此時∈。

(28)

式中=(+1)+(-1)(+)。

2.4 抗ISRJ的FSK-PSK正交波形優化算法

根據式(19)和(27)，可得目標函數對第個子脈沖的所有變量組成的向量的求導公式：

(29)

目標函數和約束條件分別對變量進行求導可用如下公式表示：

(30)

那么增廣拉格朗日函數對變量的求導公式可表示為

(31)

得到增廣拉格朗日函數對變量的求導公式后，通過增廣拉格朗日乘子法將原優化問題轉化為一個無約束的優化問題，可采用擬牛頓法進行求解。

基于FSK-PSK復合調制的抗ISRJ波形優化算法步驟如表1所示。

表1 基于FSK-PSK復合調制的抗ISRJ波形優化算法步驟

3 仿真結果與分析

定義脈內子脈沖信號的自相關平均副瓣電平(Auto-correlation Average Sidelobe Level, AASL)、互相關平均電平(Cross-correlation Average Level, CCAL)如下：

(32)

式中，=[|≤||≤′-1]表示自相關函數的副瓣范圍，=[|0≤||≤′-1]表示互相關函數范圍。

對于一組子脈沖數目=4，跳頻系數={2,1,4,3}，相位編碼碼長=50，離散相位數分別為=2/4/8的FSK-PSK信號，其相位編碼序列與PSK信號完全相同，兩種信號的AASL和CCAL值如表2所示。

表2 PSK和FSK-PSK信號對比

由表中數據可知，FSK-PSK信號相對于PSK信號，其子脈沖的自相關平均旁瓣電平是相當的，但其子脈沖互相關平均電平比PSK信號低了10 dB左右。

設置一組子脈沖數目=4，跳頻系數={1,2,3,4}，相位編碼碼長=50，離散相位數為=4的FSK-PSK信號，其各子脈沖的自相關模糊函數圖如圖3所示，從圖中可以看出， FSK-PSK復合調制信號自相關旁瓣較低，且隨著多普勒頻移增大，其自相關主峰依然保持較高水平，具有較好的多普勒頻移容忍度。

(a) 子脈沖1自相關模糊函數

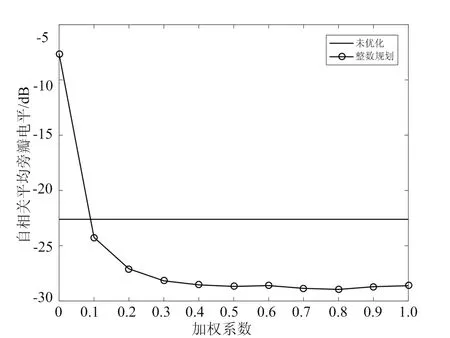
設計FSK-PSK信號的子脈沖數目=4，子脈沖信號的初始跳頻系數分別對應了={1,2,3,4}，子脈沖信號的相位編碼碼長=50，離散相位數=4。設置優化模型的加權系數分別為={0,01,…,1}，固定跳頻系數僅優化相位的FSK-PSK信號和跳頻相位聯合優化的FSK-PSK信號，其自相關和互相關優化前后結果對比如圖4所示, 具體優化數據結果如表3所示，其中初始波形=-22.610 8 dB，=-33.353 8 dB。

(a) 自相關結果對比

表3 優化后的跳頻序列和AASL、CCAL值

從圖4和表3可以看出，隨著加權系數的增加，對自相關部分的優化比重增加，而對互相關部分的優化比重相應降低，因此優化后的AASL值整體呈下降趨勢、CCAL值整體呈上升趨勢，加權系數∈[01,06]時優化后的波形相較于初始信號，其自相關旁瓣和子脈沖互相關均能得到抑制。

設置加權系數=02，FSK-PSK信號的子脈沖數目=4，子脈沖信號的相位編碼碼長=50，離散相位數=4，初始跳頻系數設為={1,2,3,4}，優化后各子脈沖跳頻系數和相位編碼信息如表4所示，各個子脈沖的自相關和互相關結果如圖5所示。從圖5可以看出，優化波形的自相關和互相關均明顯低于未優化波形。

表4 優化后的正交FSK-PSK復合調制信號

(a) 子脈沖1自相關

對一組子脈沖數=4的FSK-PSK復合調制信號，設置加權系數=02，子脈沖信號的相位編碼離散相位數=4，碼長分別為40、60、80，初始跳頻系數={1,2,3,4}，優化后的跳頻系數以及優化前后的AASL和CCAL如表5所示。

表5 不同序列長度波形優化前后性能對比

從表中數據可知，對不同長度的FSK-PSK信號序列經優化后其自相關旁瓣和互相關均能被抑制，且子脈沖序列越長，優化后的AASL和CCAL值越小，抗脈內切片轉發干擾的能力越強。

4 結束語

FSK-PSK復合調制信號比PSK信號的抗干擾性能更好，因此本文采用FSK-PSK復合調制信號作為發射波形，以最小化子脈沖的自相關旁瓣電平和各個子脈沖之間的互相關函數電平加權和為準則，用0-1離散變量表示跳頻和相位，考慮子脈沖跳頻和相位編碼序列的相位離散值的整數約束以及各子脈沖跳頻兩兩不同的約束條件，構建抗脈內切片轉發干擾的FSK-PSK正交波形設計優化問題模型，進行0-1整數規劃。將約束條件寫入增廣拉格朗日函數，通過增廣拉格朗日乘子法將原優化問題轉化為無約束優化問題，對變量求導，采用擬牛頓法求解。

本文通過仿真驗證了FSK-PSK復合調制信號與簡單形式的PSK信號相比，其子脈沖的自相關平均旁瓣電平是相當的，但其子脈沖互相關平均電平比PSK信號顯著降低，用FSK-PSK信號設計正交波形能夠提升雷達的抗干擾性能。在選取合適的加權值時，本文設計的FSK-PSK復合調制信號能夠同時有效抑制子脈沖的自相關旁瓣和互相關電平，并且其子脈沖序列長度越長，性能越好。