基于非局部自相似性的圖像去噪算法研究

郭昕剛，許連杰，霍金花，程 超

(長春工業大學計算機科學與工程學院，吉林 長春 130102)

1 引言

圖像是人類儲存和交流信息的重要方式。然而在成像系統的采集或傳播過程中，會難以避免的產生圖像噪聲。從圖像中去除噪聲是低級視覺任務中圖像質量增強不可缺少的步驟。

在以往的幾十年中，很多科研人員的工作促進了圖像去噪領域的發展。其中，許多優秀算法都使用了非局部自相似性(Non-local SelfSimilarity，NSS)。非局部自相似性采用的理論依據是圖像中通常有許多相似的面片，可以應用它們之間的聯系來進行圖像處理。2005年Buades等人設計的非局部均值(Non-local Means，NLM)去噪算法中首次使用了這一特性，之后人們廣泛關注于此方面的研究。其中Dabov等人提出了BM3D算法，構造了相似三維立體塊，在三維稀疏域中對其濾波，此算法是目前去噪算法的標桿之一。

利用圖像自身的非局部自相似性進行圖像去噪的另一個研究思路是低秩矩陣恢復(Low-Rank Matnx Recovery，LRMR)算法。該算法的原理是因為干凈圖片的矩陣是低秩的，若矩陣的元素發生改變或損壞時，可以自動恢復發生改變的元素。采用核范數最小化(NNM)可替代低秩矩陣，NNM對特定的保真度函數和非凸優化的低秩矩陣能夠找到全局最優解。但是NNM的缺點是對奇異值一致處理，這會造成數據偏差。為解決這個問題，Gu等提出了(Weighted Nuclear Norm Minimization，WNNM)算法，權重的分配隨奇異值的不同而改變，能更好的恢復低秩矩陣。

上述的基于NSS的算法都取得了很好的去噪性能，其中WNNM算法是目前性能較好的算法之一。但該算法中圖像塊之間的相似度是依靠歐氏距離來評判，這種評判方法雖然效果良好，但在噪聲的影響下，該方法計算出來的相似性可能會出現偏差，例如把某些相似度不高的圖像塊定為匹配圖像塊，這會影響最終的去噪性能。另外，在上述算法中，NSS先驗都是基于在整個圖像中尋找相似的面片。但是為圖像中的所有參考面片都找到非常相似的面片是十分具有挑戰性的，尤其是當相似面片的數量很大時。而如果尋找的面片匹配度不高，則會影響權重分配并使去噪圖像模糊。為了突破這一瓶頸，BM3D-SAPCA提出了搜索形狀自適應相似面片的策略。然而，這會在去噪圖像中產生隨機的形狀偽影。

本文首先針對在圖像中尋找非常相似的圖像塊十分困難的問題，在面片級的相似矩陣基礎上進一步搜索相似像素，獲得了像素級相似矩陣，并基于相似像素矩陣提出一種噪聲水平估計方式。另外針對WNNM算法在計算圖像塊相似度時容易收到噪聲影響的問題，首先采用哈爾變換和維納濾波進行對噪聲圖像進行預處理，通過預處理操作降低圖像中的噪聲，從而降低噪聲引起的誤差值，獲得相似度更高的圖像塊。然后將預處理圖像的像素級相似矩陣塊組輸入到WNNM算法中進行最終去噪。實驗結果表明，所提算法的客觀指標和主觀視覺效果都十分優異。

2 理論基礎

2.1 像素級NSS先驗

NSS是圖像去噪的有力先驗，大部分先進的去噪算法中都有對NSS的應用。首次采用NSS先驗的NLM方法是通過計算圖像中特定范圍像素的值，對其取平均值來估計某個位置的像素值，其中權重由相應圖像塊之間的相似性來確定。雖然這是像素級的方法，但NLM是根據面片級別的NSS執行降噪，且復雜度很高。BM3D中采用的面片級別的NSS先驗是對在非局部區域中搜索到的相似塊組執行去噪。這些方法通常假設收集的相似面片是完全匹配的。在本文中，采用了進一步搜索相似像素的方法。

(1)

(2)

2.2 噪聲水平估計

(3)

假設共有個面片，將噪聲水平估計從局部區域擴展到全局區域，則全局的噪聲水平可設置為

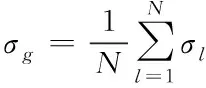
(4)

所提出的基于像素的噪聲水平估計方法非常簡單，因為它只計算從圖像中提取的最相似像素之間的距離。在BSD68數據集上測試本文噪聲估計算法的準確性，并與當前主流的噪聲估計方法相比較，包括Zoran算法，Liu算法，Chen算法，表1為幾種算法噪聲水平估計均值對比，加黑的為最小偏差數值。

表1 幾種算法的噪聲估計值

通過比較表中數據可知所提出的噪聲水平估計方法十分精確，并且在高噪聲的情況下效果更好。

2.3 WNNM算法

對于噪聲圖像，先確定它的某個局部面片，在圖像的特定范圍中搜索它的相似塊，把它們聚集為一個矩陣，記為。令=+，式中是清晰圖像塊，是一個低秩矩陣，是噪聲塊。之后采取WNNM算法來完成低秩矩陣的還原。WNNM函數可以表示為

(5)

式中

(6)

式中≥0是()的權重，的計算式為

(7)

式中，為大于0的常數；為中相似圖像塊的個數；=10的作用是避免除數為零。之后使用奇異值分解得到全局最優解，即

(8)

=()=max(()-，0)

(9)

(10)

式中，()表示為的奇異值。

3 本文算法

本文的去噪算法流程如圖1所示，可分為三個階段來實現。

圖1 本文算法去噪流程圖

3.1 基于哈爾變換進行初步去噪預估計

(11)

(12)

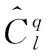
(13)

其中∈×，∈×。

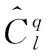
3.2 通過迭代維納濾波進行預處理去噪

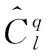
(14)

(15)

在這里，如式(14)和(15)所示，原始噪聲圖像矩陣塊和預估計像素矩陣塊都是必需的。實驗表明，維納濾波兩次迭代效果最佳，而多迭代的去噪效果會下降。濾波后對去噪后的變換系數執行逆哈爾變換得到預處理的相似矩陣塊組，將其輸入WNNM進行最終去噪。

3.3 通過WNNM最終去噪

首先將預處理后的相似矩陣塊組用(4)式進行噪聲水平估計，利用估計的噪聲方差來歸一化WNNM算法中F范數的保真項，保證WNNM算法能在去除噪聲的同時保護有效信號，同時輸入預處理后的相似矩陣塊組，利用WNNM算法對其殘余噪聲及偽影進一步去噪，之后通過迭代去噪后聚合得到最終的去噪圖像。此處WNNM算法的求解步驟為：

綜上所述，本文提出的算法首先對噪聲圖像提取像素級的相似塊組，然后對其進行哈爾變換與維納濾波進行預處理，最后將預處理圖像的相似塊組與估計的噪聲方差輸入WNNM進行最終去噪。此算法的優勢在于：

1) 像素級NSS比面片級NSS更能利用圖像的非局部自相似性，且隨之提出的噪聲水平估計算法也很準確，從而可以提供相似度更高的相似塊矩陣和精確的噪聲估計用于去噪；

2) 經過預處理后的圖像相似塊組一方面更好的利用了干凈圖像的先驗知識，另一方面隨著噪聲減少，信噪比會增加，此時因噪聲引起的誤差值部分也會減小，之后采用WNNM算法可以取得更好的去噪效果。

4 對比實驗分析

為了驗證本文算法的去噪性能，選用了圖像處理經典的Set12數據集中的圖片來進行仿真。測試環境為：Intel(R) Core(TM) i5-6200U CPU，RAM=8GB，仿真軟件為Matlab2014a，將本文的算法與當前效果最好的幾種方法進行了比較，其中包括K-SVD、BM3D、WNNM、PCLR、NCSR。本文實驗的圖像大小都設定為 256 ×256 像素，同時設定均值為0，標準差σ分別為20、40、60和100的高斯白噪聲環境。

實驗中用PSNR和SSIM值來作為評價指標，各個算法對比結果如表2所示，其中加黑的為最高值。從表2中可以看到，無論是在低噪聲還是高噪聲的條件下，本文算法的PSNR和SSIM值都比K-SVD、BM3D、WNNM和NCSR算法高。對于PCLR算法，在σ=20和σ=40的Lena圖像上PSNR值與本文算法不相上下，但在其它圖像或者高噪聲的條件下，本文算法的PSNR值都要高于PCLR算法。相較五幅測試圖像的PSNR和SSIM的平均值而言，本文算法在各個噪聲條件下的客觀評價指標都是最高的。需要特別關注的是，本文算法在中高噪聲條件下的表現更為突出。例如在σ=100的情況下，即便相較于其中效果最好的WNNM算法，本文算法的平均PSNR值仍提高約0.44dB，SSIM值提升約0.03。

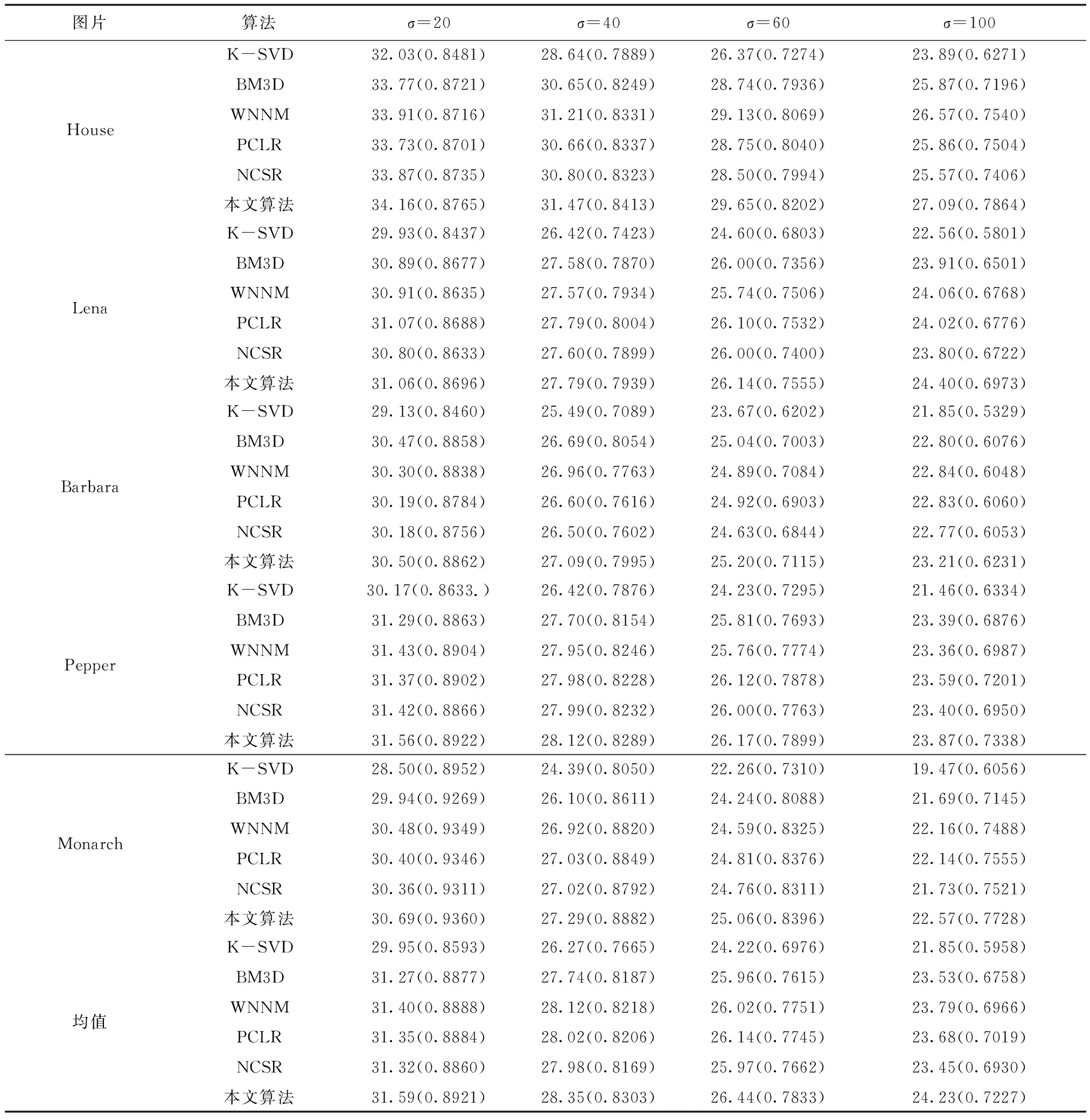
表2 幾種算法的PSNR(SSIM)值對比

為了體現去噪圖像的直觀視覺效果，圖2～5顯示了各個去噪算法去噪結果的整體圖像和局部細節對比圖像。其中圖2是House圖像在σ=40情況下幾種算法的整體去噪結果，圖3為其局部屋檐細節放大圖。

圖2 σ=40下House圖像去噪結果對比圖

從House整體圖像上能夠直觀的看出，K-SVD、BM3D和PCLR算法會產生不同程度的偽影，而WNNM和PCLR算法會出現噪聲白斑。從House圖像的細節對比圖片來看，KSVD、NCSR算法有嚴重偽影，BM3D、WNNM和PCLR算法也會產生模糊的紋理結構。而本文算法得到的去噪圖片整體觀感較為清晰且對局部結構的處理也較為平滑。

圖3 σ=40下House圖像局部細節對比圖

圖4 σ=100下Monarch圖像去噪結果對比圖

圖5 σ=100下Monarch圖像局部細節對比圖

圖4是Monarch圖像在σ=100時幾種算法的整體去噪結果，圖5為其局部翅膀結構細節的放大圖。從Monarch圖像對比圖片中可以看出，在高噪聲的情況下，KSVD和BM3D算法去噪后的圖片整體視覺效果模糊，而從細節對比圖片中可以看出WNNM、PCLR和NCSR算法會在條紋處引入大量偽影。相比之下本文算法仍然可以有較為清晰的整體觀感，且偽影更少。從翅膀的放大圖片來看，本文算法能夠更為清晰的保持圖像的細節結構。

5 結束語

本文提出了一種新的基于非局部自相似性的圖像去噪算法，首先在面片級的相似塊矩陣中進一步縮小范圍，獲得更加精確的像素級相似塊矩陣，可以更大程度的利用NSS先驗，并提出一種基于像素級相似塊矩陣的噪聲水平估計算法。然后基于哈爾變換和維納濾波對噪聲圖片進行預處理去噪，預處理后的圖像一方面更好的利用了干凈圖像的先驗知識，另一方面預處理后的圖像噪聲水平下降，因噪聲引起的誤差值部分也隨之減小。最后使用本文噪聲估計算法對預處理圖像的相似矩陣塊組進行噪聲估計，用估計得到的噪聲方差來歸一化WNNM算法中的保真項，保證WNNM算法能在壓制噪聲的同時保護有效信號，利用WNNM方法對其殘余噪聲及偽影做進一步去噪處理。實驗結果表明與已有算法相比，所提算法的客觀指標有所提高，且去噪后的圖像偽影較少，圖像紋理細節更為清晰，同時在高噪聲水平下表現更為突出。