一種改進牛頓-拉夫遜ERT算法

周 曦，柴曉宇，王 彬，肖理慶

(淮南師范學院機械與電氣工程學院，安徽 淮南 232038)

1 引言

作為電學層析成像技術的重要分支，目前電阻層析成像技術在可視化檢測領域中已得到了飛速發展。其中，利用圖像重建算法計算得到敏感場邊界電壓測量值對應的敏感場域內電阻率分布，不僅是電阻層析成像技術的核心內容，也是目前國內外科學工作者研究的難點與熱點。

為了提高重建圖像分辨率，文獻[6]利用仿真圖像作為訓練樣本，提出了一種將長短期記憶網絡與卷積神經網絡結合的ERT圖像重建算法，并通過了礦山充填管道可視化檢測平臺的驗證；文獻[7]提出了一種長短期記憶神經網絡+全連接神經網絡ERT圖像重建算法；文獻[8]提出了稀疏正則化算法，獲得了更高精度的重建圖像；文獻[9]提出了一種可有效減小偽影的ERT重建算法。

修正牛頓-拉夫遜算法是具有最優化思想的靜態圖像重建算法，但圖像重建質量很大程度上取決于初始電阻率分布估計值選取、正則化因子調整策略以及靈敏度矩陣更新策略。而遺傳算法作為一種群體型操作算法，被廣泛應用于不同優化問題求解。本文在確定初始電阻率分布估計值選取、正則化因子調整策略以及靈敏度矩陣更新策略的基礎上，將區間算法引入文獻[15]所提出的改進遺傳算法中，并將其應用于重建圖像閾值優化，有效提高了重建圖像分辨率。

2 改進牛頓-拉夫遜算法

2.1 初始電阻率分布估計值選取

為了在保證算法逆問題求解過程收斂的前提下，提高算法實時性，在敏感場域內介質分布的初始值選取方面，利用可實現離線優化與計算、在線一步成像的改進Landweber預迭代算法獲得，具體迭代公式如式(1)所示。

+1=+1·(·)

(1)

式中：+1為第+1次預迭代時對應的重建圖像灰度值，為離線優化所得對角陣，為敏感場邊界電壓測量值，+1的離線計算公式如式(2)與式(3)所示。

+1=+(-)

(2)

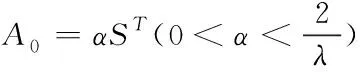
(3)

式中：為單位矩陣，為增益因子，為方陣的最大特征值。

2.2 正則化因子調整策略

在修正牛頓-拉夫遜圖像重建算法逆問題求解過程中，按式(4)修正敏感場域Ω內介質電阻率分布。

(+1)=()+Δ(+1)

(4)

式中：(+1)=()+Δ(+1)為第+1次迭代時對應的敏感場域Ω內介質電阻率分布，Δ(+1)為修正量，計算公式如式(5)所示。

Δ(+1)=-{[′(())]′(())+()}

·[′(())]((())-)

(5)

式中：′(())與(())分別為敏感場域Ω內介質電阻率分布為()時對應的靈敏度矩陣和敏感場邊界電壓計算值，()為正則化因子。

為了保證逆問題求解過程穩定且圖像重建精度滿足要求，借鑒慣性權重遞減策略，正則化因子()按概率采取式(6)-式(8)所示三種不同遞減策略調整。

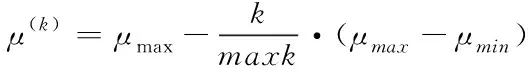
(6)

()=+(-)·(-)

(7)

()=+(-)·(-)

(8)

式中：與根據經驗知識設置，與分別為迭代次數最大值與當前值。

2.3 靈敏度矩陣更新策略

關于靈敏度矩陣更新策略，目前在電阻層析成像迭代類圖像重建算法中，通常采用以下兩種措施：

①靈敏度矩陣固定不變。這種措施一般選取敏感場域Ω內介質電阻率均勻分布對應的靈敏度矩陣，雖然可滿足對圖像重建算法實時性的要求，但逆問題求解精度不高且收斂速度較慢。即使通過優化措施保證逆問題求解過程穩定，但重建圖像分辨率仍很難滿足要求。

②靈敏度矩陣時刻更新。與上一種措施相比，這種措施雖然圖像重建精度較高，但逆問題求解速度難以滿足要求，而且在更新靈敏度矩陣時，如果敏感場域Ω內介質電阻率與其真實情況相差較大，反而會降低圖像重建算法逆問題求解精度。

針對上述兩種措施的不足之處，本文提出一種新型靈敏度矩陣更新策略：在算法逆問題求解過程中，將第次計算所得敏感場邊界電壓計算值()代入式(9)，如果誤差不再減小，則按目前所得的敏感場域Ω內介質電阻率最優分布更新靈敏度矩陣。

(9)

2.4 重建圖像閾值優化

當更新靈敏度矩陣無法繼續減小敏感場邊界電壓計算值與測量值的誤差時，為了進一步提高圖像重建算法逆問題求解的精度和速度，將區間算法引入文獻[15]所提出的改進遺傳算法中，將滿足式(10)、不存在極值點的區間排除，在可能存在極值點的區間生成改進遺傳算法初始種群，并利用所提出的改進遺傳算法優化目前所得的敏感場域Ω內介質電阻率最優分布對應的重建圖像閾值和，如式(11)所示，進而可得敏感場域Ω內電阻率分布的最終最優值。

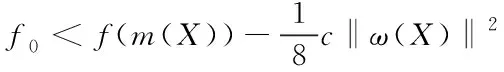
(10)

式中：為()在內某點的適應值，?表示任一區間，為萊布尼茲常數，()和()分別為區間的寬度和中點。

(11)

式中：為求解逆問題時敏感場域Ω內剖分的三角形有限元數目。

3 仿真與分析

圖1 敏感場域Ω內六種不同典型分布

現通過正問題計算，獲得敏感場邊界電壓測量值，為了避免“inverse crime”并提高算法圖像重建的速度，利用細化前的有限元模型求解電阻層析成像逆問題。當圖像重建算法最大迭代次數maxk均設置為200時，不同圖像重建算法逆問題求解結果分別如圖2-圖7、表1及表2所示。

圖2 無噪聲干擾時算法1逆問題求解結果

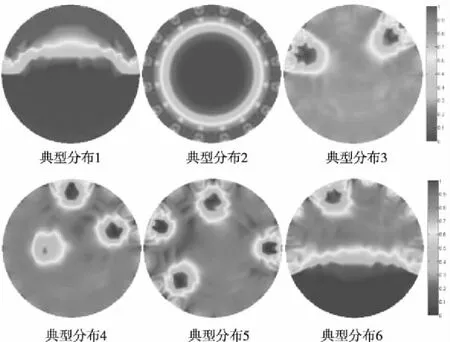
圖3 無噪聲干擾時算法2逆問題求解結果

圖4 無噪聲干擾時算法3逆問題求解結果

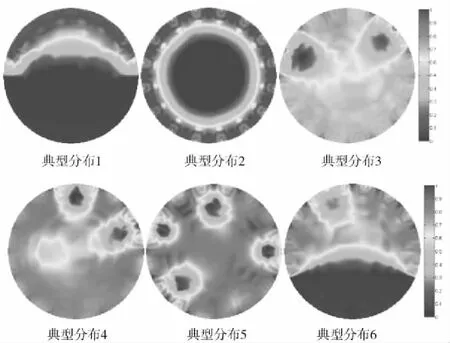
圖5 有噪聲干擾時算法1逆問題求解結果

圖6 有噪聲干擾時算法2逆問題求解結果

圖7 有噪聲干擾時算法3逆問題求解結果

表1 無噪聲干擾時不同算法相關系數ρ比較

表2 有噪聲干擾時不同算法相關系數ρ比較

其中圖像重建算法1在逆問題求解過程中采取固定敏感場域Ω內介質電阻率均勻分布對應的靈敏度矩陣不變的策略，而正則化因子()采取式(7)所示遞減策略調整，并根據算法收斂次數與發散次數分別按式(12)與式(13)更新正則化因子最大值與算法最大迭代次數，圖像重建算法2在逆問題求解過程中采取每次迭代均更新靈敏度矩陣的策略，正則化因子()按式(8)調整，圖像重建算法3為本文提出的改進算法，本文所采取的評價圖像重建算法逆問題求解精度的相關系數的計算公式如式(14)所示。

(12)

(13)

式中：與分別為正則化因子縮小倍數與放大倍數。

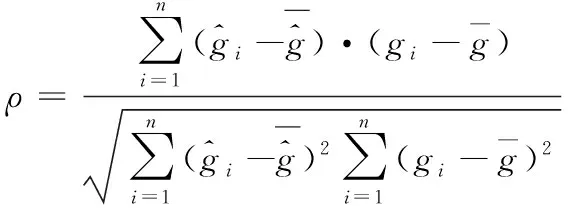
(14)

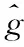
對比圖1設置的敏感場域Ω內六種不同典型分布與圖2-圖7不同圖像重建算法逆問題求解結果，并結合表1與表2在無噪聲干擾和有噪聲干擾時不同算法相關系數，可得以下結論：

①對不同圖像重建算法而言，噪聲干擾均會影響逆問題求解精度：在無噪聲干擾時，圖像重建算法1-3相關系數的平均值分別為08360、08555、08828，在有噪聲干擾時，圖像重建算法1-3相關系數的平均值分別減小至08092、08276、08572，分別降低了32057、32613、28999。

②相比在逆問題求解過程中采取固定敏感場域Ω內介質電阻率均勻分布對應的靈敏度矩陣不變策略的圖像重建算法1，在逆問題求解過程中采取每次迭代均更新靈敏度矩陣策略的圖像重建算法2雖然計算量較大，需消耗大量時間反復計算靈敏度矩陣，但逆問題求解精度較高：針對圖1設置的敏感場域Ω內六種不同典型分布，相比圖像重建算法1，在無噪聲干擾和有噪聲干擾時，圖像重建算法2相關系數的平均值分別提高了23325、22739。

③在三種不同圖像重建算法中，由于本文提出的圖像重建算法3采取了不同措施減小敏感場邊界電壓計算值與測量值的誤差，因此逆問題求解精度更高：針對圖1設置的敏感場域Ω內六種不同典型分布，相比逆問題求解精度較高的圖像重建算法2，在無噪聲干擾和有噪聲干擾時，本文提出的圖像重建算法3相關系數的平均值分別提高了31911、35766。

4 結論

為了提高重建圖像分辨率，針對目前公認的逆問題求解精度比較理想、具有最優化思想的修正牛頓-拉夫遜圖像重建算法，從初始電阻率分布估計值選取、正則化因子調整策略、靈敏度矩陣更新策略以及重建圖像閾值優化等四個方面對算法進行了改進：

①將改進Landweber預迭代算法的圖像重建結果作為初始電阻率分布估計值。

②在算法逆問題求解過程中，按概率采取三種不同遞減策略調整調整正則化因子。

③在算法逆問題求解過程中，當敏感場邊界電壓計算值與測量值的誤差不再減小時，按目前所得的敏感場域內介質電阻率最優分布更新靈敏度矩陣。

④當更新靈敏度矩陣無法繼續減小敏感場邊界電壓計算值與測量值的誤差時，利用所提出的改進遺傳算法優化目前所得的敏感場域內介質電阻率最優分布對應的重建圖像閾值。

最后，通過設置敏感場域內六種不同典型分布并在相同實驗條件下利用不同圖像重建算法求解逆問題，驗證了所提出的改進牛頓-拉夫遜算法在無噪聲干擾和有噪聲干擾時均可有效提高重建圖像分辨率。