地鐵浮置板軌道系統(tǒng)導(dǎo)納特性與鋼軌波磨關(guān)系研究

陸文學(xué)，楊新文，趙治均

（1.蘇州市軌道交通集團(tuán)有限公司，江蘇蘇州 215004；2.同濟(jì)大學(xué)交通運(yùn)輸工程學(xué)院，上海 201804）

鋼軌波磨作為鋼軌表面?zhèn)麚p類型之一，加劇了輪軌相互作用，引發(fā)了車輛和軌道的強(qiáng)烈振動(dòng)[1]，進(jìn)而誘發(fā)在鋼軌波磨區(qū)段存在如扣件彈條斷裂失效、鋼軌疲勞裂紋轉(zhuǎn)向架開(kāi)裂和輪軌噪聲加劇等問(wèn)題[2]。因此，鋼軌波磨不僅增加了軌道交通的維修成本和降低旅客舒適度，而且也會(huì)直接威脅運(yùn)營(yíng)安全。

對(duì)鋼軌波磨的發(fā)生機(jī)理、特征以及控制措施進(jìn)行了多年的研究，厘清鋼軌波磨的發(fā)生機(jī)理是控制波磨的前提，目前最為大家所認(rèn)可的機(jī)理是固定波長(zhǎng)機(jī)理和損傷機(jī)理，其中，固定波長(zhǎng)機(jī)理一般指由于鋼軌的Pinned-Pinned 共振、P2共振和驅(qū)動(dòng)輪對(duì)2 階扭振等原因引起鋼軌形成某一特定波長(zhǎng)的波磨，這種波磨的波長(zhǎng)穩(wěn)定。損傷機(jī)理一般指輪軌系統(tǒng)一旦產(chǎn)生粘滑振動(dòng)，磨耗功即出現(xiàn)劇烈持續(xù)的波動(dòng)，磨耗功的波動(dòng)致使鋼軌表面產(chǎn)生不均勻磨損。單個(gè)車輪對(duì)鋼軌的不均勻磨損是非常微小的,但在通過(guò)曲線車輛眾多車輪的長(zhǎng)期作用下，鋼軌表面不均勻磨損積累，并最終發(fā)展為鋼軌表面的波磨。Grassie[3]將波磨按照不同的固定波長(zhǎng)機(jī)理和損傷機(jī)理分為響軌波磨、車轍型波磨、P2力共振波磨、重載波磨、輕軌波磨和軌道形式波磨六類。劉學(xué)毅[4]按照波磨是否由輪軌系統(tǒng)振動(dòng)的動(dòng)力效應(yīng)主導(dǎo)將其成因歸納為動(dòng)力類成因理論和非動(dòng)力類成因理論兩類。金學(xué)松等[5]按照波磨是與系統(tǒng)固有特性相關(guān)還是由初始不平順發(fā)展而來(lái)，將其成因總結(jié)為自激振動(dòng)理論、反饋振動(dòng)理論和其他理論三類。近年來(lái)，我國(guó)地鐵線路也出現(xiàn)了普遍的鋼軌波磨問(wèn)題[6-8]，產(chǎn)生機(jī)理較為復(fù)雜，學(xué)者們也通過(guò)理論模型與試驗(yàn)測(cè)試等手段進(jìn)行了系統(tǒng)研究。鋼軌波磨發(fā)生機(jī)理復(fù)雜，影響因素眾多，與整個(gè)車輛-軌道結(jié)構(gòu)系統(tǒng)中各個(gè)部分均有一定關(guān)聯(lián)，至今未有一種統(tǒng)一的機(jī)理解釋各種波磨現(xiàn)象。

為了控制環(huán)境振動(dòng)問(wèn)題，地鐵線路中也鋪設(shè)了浮置板軌道結(jié)構(gòu)，浮置板軌道作為一種有效的減振軌道結(jié)構(gòu)，較好地控制列車引起的環(huán)境振動(dòng)的影響，但近年來(lái)鋼彈簧浮置板軌道區(qū)段也出現(xiàn)了鋼軌波磨問(wèn)題[9]，已有研究主要通過(guò)現(xiàn)場(chǎng)觀測(cè)的一些規(guī)律進(jìn)行了定性詮釋[10]，而對(duì)于鋼彈簧浮置板地段鋼軌波磨的產(chǎn)生機(jī)理理論仿真和輪軌系統(tǒng)參數(shù)影響分析等方面的研究較少。

為了探明鋼彈簧浮置板軌道區(qū)段波磨發(fā)生機(jī)理及與輪軌系統(tǒng)參數(shù)影響規(guī)律，本文首先基于現(xiàn)場(chǎng)測(cè)試的鋼軌波磨特征，分析波磨典型波長(zhǎng)及其通過(guò)頻率；其次建立輪對(duì)和鋼彈簧浮置板軌道三維有限元模型，分析輪軌共振模態(tài)與浮置板軌道鋼軌導(dǎo)納特性；最后探討鋼軌扣件剛度、浮置板隔振器剛度與輪對(duì)振動(dòng)模態(tài)對(duì)鋼彈簧浮置板區(qū)段鋼軌波磨的影響規(guī)律。

1 地鐵浮置板軌道波磨測(cè)試

1.1 現(xiàn)場(chǎng)測(cè)試概況

測(cè)試區(qū)間位于蘇州地鐵2號(hào)線，2號(hào)線是蘇州軌道交通骨干性線路，總體呈南北走向，全長(zhǎng)42.046 km，起于相城區(qū)太平車輛段以西騎河路站，終于園區(qū)桑田島站。自開(kāi)通運(yùn)營(yíng)以來(lái)，在小半徑曲線上尤其鋼彈簧浮置板軌道區(qū)段鋼軌波磨日益嚴(yán)重。選取桐涇公園站-友聯(lián)站（上行）區(qū)間上一條曲線進(jìn)行測(cè)試，測(cè)試軌道曲線所在位置，如圖1 所示，曲線里程為K20+175～K20+564，長(zhǎng)度389 m，曲線半徑350 m，軌道結(jié)構(gòu)為鋼彈簧浮置板軌道，扣件為DTⅥ2型扣件。

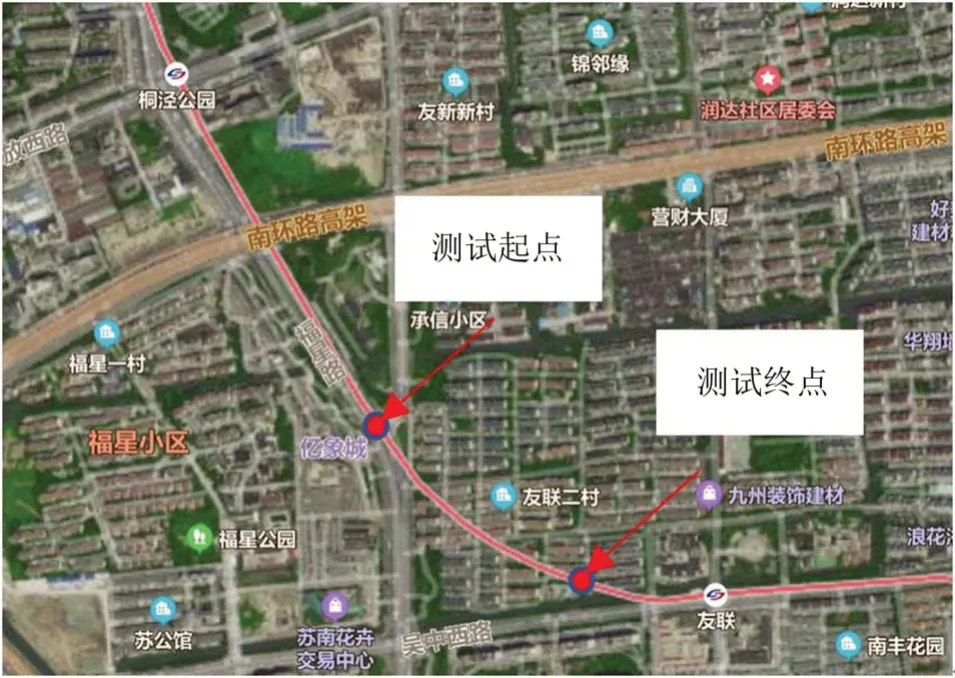
圖1 波磨現(xiàn)場(chǎng)測(cè)量位置

1.2 測(cè)試結(jié)果

從線路曲線測(cè)量得到了軌面不平順數(shù)據(jù)中繪制內(nèi)、外軌軌面不平順?lè)惦S里程的變化波形，如圖2所示。

采用國(guó)際標(biāo)準(zhǔn)Ⅰnternational Organization for Standardization（ⅠSO）3095[11]對(duì)軌面不平順進(jìn)行頻譜分析，得到實(shí)測(cè)軌面不平順頻譜與ⅠSO 3095 標(biāo)準(zhǔn)軌面不平順頻譜的對(duì)比結(jié)果，如圖3所示。

由圖3 可知，軌面不平順波長(zhǎng)在50 mm～900 mm 內(nèi)，內(nèi)外軌表面不平順?biāo)骄闯^(guò)ⅠSO 3095規(guī)定的標(biāo)準(zhǔn)值；軌面不平順波長(zhǎng)在24.2 mm～50 mm范圍內(nèi)，內(nèi)軌表面不平順?biāo)匠^(guò)了ⅠSO 3095 規(guī)定的標(biāo)準(zhǔn)值，在31.7 mm附近出現(xiàn)一個(gè)明顯峰值，而外軌表面不平順低于ⅠSO 3095 規(guī)定的標(biāo)準(zhǔn)值；在軌面不平順波長(zhǎng)小于50 mm內(nèi)內(nèi)外軌表面不平順?biāo)骄陀冖馭O 3095規(guī)定的標(biāo)準(zhǔn)值。經(jīng)過(guò)對(duì)現(xiàn)場(chǎng)測(cè)試數(shù)據(jù)（如圖2）的局部分析，發(fā)現(xiàn)內(nèi)軌表面10 米范圍內(nèi)出現(xiàn)了波長(zhǎng)為31.7 mm的持續(xù)有規(guī)律的波谷和波深等波磨特征。

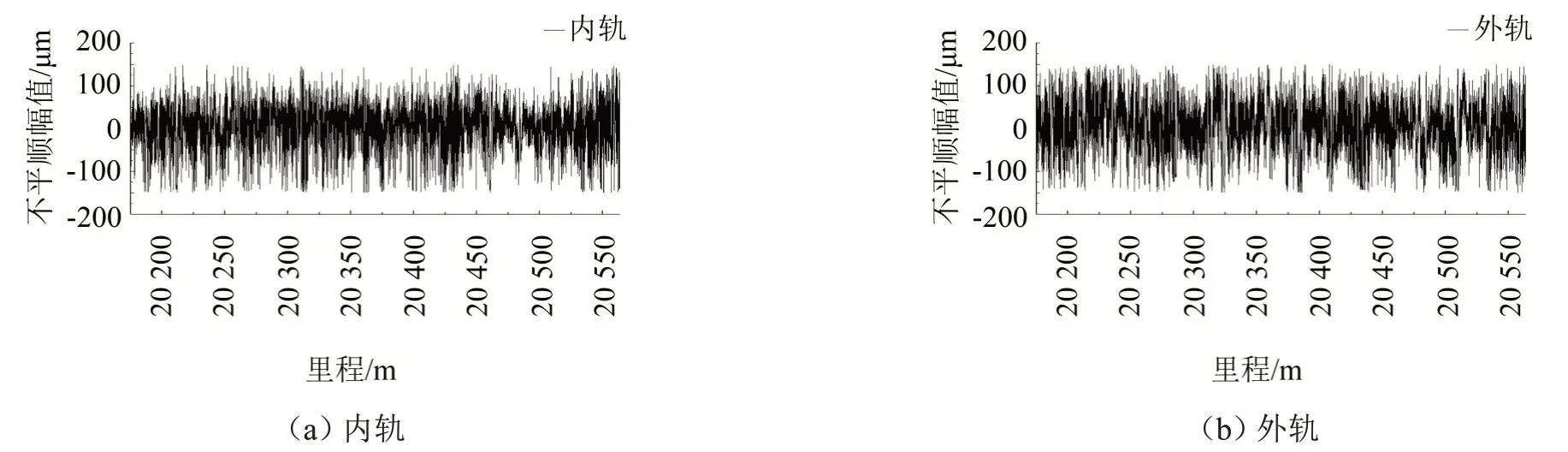
圖2 軌面不平順?lè)祱D

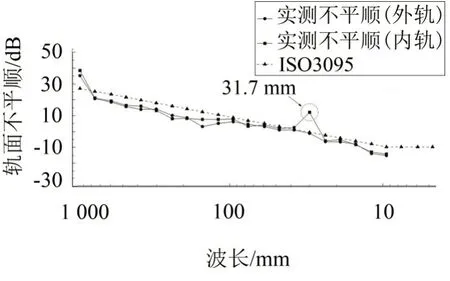
圖3 鋼軌軌面不平順?lè)治鰧?duì)比

2 浮置板軌道和輪對(duì)有限元模型

2.1 浮置板軌道有限元模型

為了系統(tǒng)研究分析城市軌道交通鋼彈簧浮置板區(qū)段的鋼軌振動(dòng)特性，利用非線性有限元分析軟件Abaqus，建立了浮置板軌道結(jié)構(gòu)三維實(shí)體有限元模型。軌道結(jié)構(gòu)有限元模型的參數(shù)參考蘇州城市軌道交通實(shí)際建設(shè)線路的設(shè)計(jì)參數(shù)，其橫截面尺寸參數(shù)如圖4 所示，建立有限元模型所需要的軌道動(dòng)力學(xué)參數(shù)如表1所示。

表1 有限元模型的動(dòng)力學(xué)參數(shù)

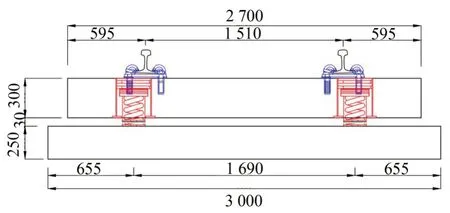
圖4 鋼彈簧浮置板軌道系統(tǒng)橫截面示意圖（單位：mm）

對(duì)所建立的軌道系統(tǒng)三維實(shí)體有限元模型，使用Lanczos法進(jìn)行軌道系統(tǒng)的模態(tài)分析，提取軌道系統(tǒng)的固有頻率和對(duì)應(yīng)模態(tài)。為降低模型中鋼軌和軌下結(jié)構(gòu)內(nèi)部的應(yīng)力波在端部反射對(duì)軌道結(jié)構(gòu)振動(dòng)特性的影響，模型需要足夠的縱向長(zhǎng)度。

參考國(guó)內(nèi)外有關(guān)文獻(xiàn)的計(jì)算模型設(shè)計(jì)，確定軌道系統(tǒng)的模型長(zhǎng)度為25 m，可以反映車輛運(yùn)行過(guò)程中近似無(wú)限長(zhǎng)鋼軌的振動(dòng)特性。軌道系統(tǒng)結(jié)構(gòu)在橫截面上都是對(duì)稱結(jié)構(gòu)，為提高計(jì)算速度，可建立單股軌道結(jié)構(gòu)模型，設(shè)置對(duì)稱邊界，最終建立三維有限元模型，如圖5所示。

由圖5 可知，浮置板軌道從上而下，分別由鋼軌、扣件、浮置板、隔振器和支撐層構(gòu)成。

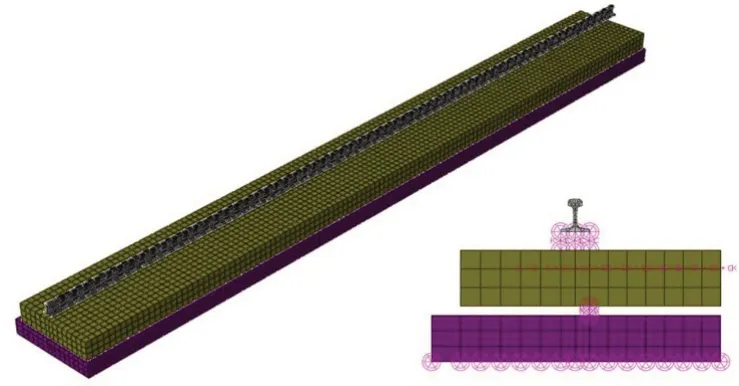
圖5 鋼彈簧浮置板軌道有限元模型

2.2 輪對(duì)有限元模型

對(duì)于地鐵車輛輪對(duì)的建模，同樣參考蘇州城市軌道交通廣泛運(yùn)營(yíng)使用的B型電客車的有關(guān)設(shè)計(jì)數(shù)據(jù)，建立地鐵車輛輪對(duì)的三維實(shí)體有限元模型，如圖6所示。

圖6 車輛輪對(duì)有限元模型

3 鋼彈簧浮置板軌道導(dǎo)納特性與鋼軌波磨關(guān)系分析

3.1 浮置板軌道導(dǎo)納特性

鋼彈簧浮置板軌道系統(tǒng)的鋼軌垂向位移導(dǎo)納曲線，如圖7所示，其中垂向鋼軌位移導(dǎo)納頻率范圍在0～10 000 Hz內(nèi)，步長(zhǎng)為1 Hz。

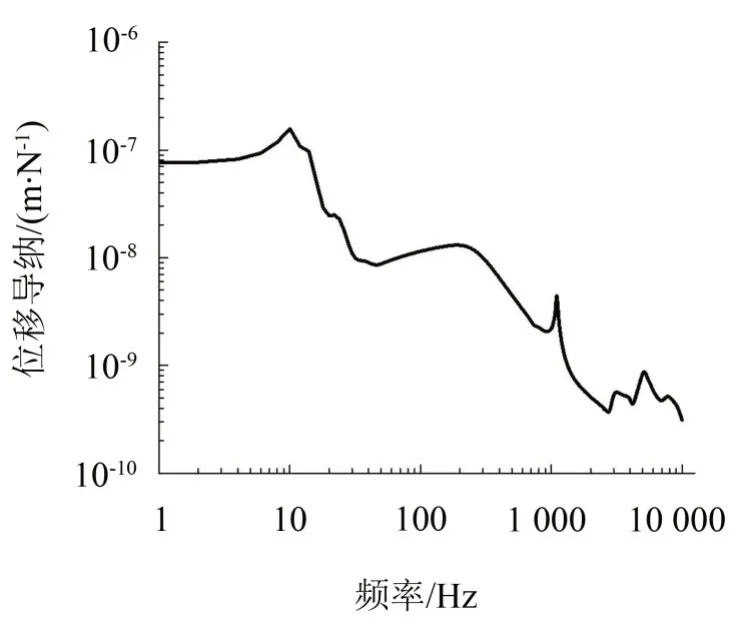
圖7 鋼彈簧浮置板軌道的鋼軌垂向位移導(dǎo)納

由圖7可知，在2 000 Hz以下頻段，鋼軌有三種典型的振動(dòng)形式，對(duì)應(yīng)各個(gè)導(dǎo)納峰值：鋼軌與浮置板整體垂向沉浮運(yùn)動(dòng)、鋼軌從扣件上起跳振動(dòng)和垂向1階pinned-pinned 共振。其中，鋼軌與浮置板整體垂向沉浮運(yùn)動(dòng)，在10 Hz左右；鋼軌起跳振動(dòng)頻率大約在190 Hz，而鋼軌pinned-pinned 振動(dòng)是指支撐于兩個(gè)扣件之間的鋼軌受到激勵(lì)后產(chǎn)生的縱向振動(dòng)波，其駐波節(jié)點(diǎn)剛好在扣件處。在2 000 Hz以上頻段出現(xiàn)的峰值均屬于多階鋼軌垂向pinned-pinned 共振，對(duì)應(yīng)頻率為1 100 Hz，3 162 Hz，5 140 Hz 和7 796 Hz。

鋼彈簧浮置板軌道系統(tǒng)的鋼軌橫向位移導(dǎo)納曲線，如圖8所示。

由圖8可知，鋼軌在1 000 Hz以下頻段，有四個(gè)峰值，其中第一個(gè)橫向鋼軌峰值頻率為100 Hz，第二個(gè)為橫向pinned-pinned 振動(dòng)峰值，頻率為548 Hz。在大于1 000 Hz 以上頻段，鋼軌橫向pinned-pinned振動(dòng)頻率為1 958 Hz。

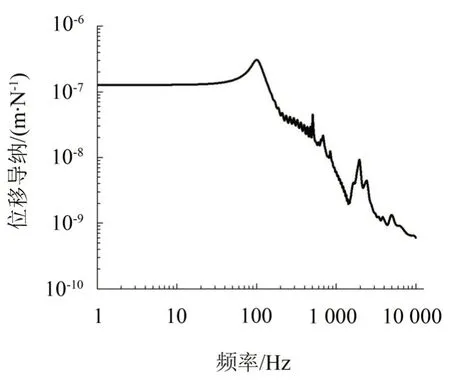
圖8 鋼彈簧浮置板軌道的鋼軌橫向位移導(dǎo)納

3.2 扣件剛度的影響分析

（1）扣件垂向剛度：

采用單變量設(shè)計(jì)方法來(lái)研究扣件剛度對(duì)浮置板系統(tǒng)導(dǎo)納的影響規(guī)律。首先考慮扣件垂向剛度的可變，在保持其他參數(shù)不變的情況，分別將扣件垂向剛度取值5 kN/mm、10 kN/mm、20 kN/mm、30 kN/mm、40 kN/mm 和50 kN/mm，計(jì)算分析這六種工況鋼軌跨中簡(jiǎn)諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的垂向?qū)Ъ{，結(jié)果如圖9所示。

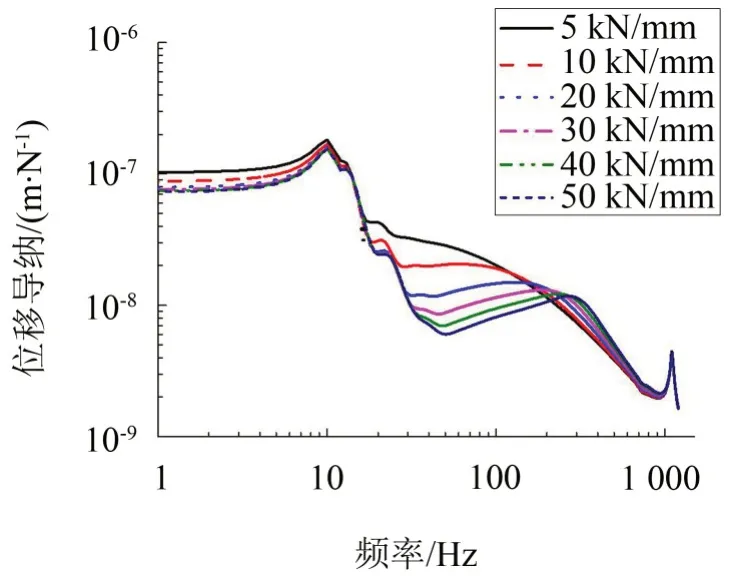
圖9 扣件垂向剛度對(duì)鋼軌垂向?qū)Ъ{的影響

由圖9 可知，改變鋼彈簧浮置板軌道系統(tǒng)的扣件垂向剛度，對(duì)鋼軌垂向?qū)Ъ{的影響規(guī)律為：在1 Hz～10 Hz 頻段，隨著鋼軌扣件垂向剛度增大，鋼軌垂向?qū)Ъ{也相應(yīng)降低；在10 Hz～20 Hz頻段，鋼軌導(dǎo)納幾乎不受扣件剛度的影響；在20 Hz～200 Hz 頻段，隨著鋼軌扣件垂向鋼軌的增大，鋼軌垂向?qū)Ъ{相應(yīng)降低；在200 Hz～1 000 Hz頻段，隨著鋼軌扣件垂向鋼軌的增大，鋼軌垂向?qū)Ъ{相應(yīng)增大。可見(jiàn)，在1 000 Hz 以下時(shí)，鋼軌扣件垂向剛度對(duì)鋼軌垂向?qū)Ъ{的影響較大。

（2）扣件橫向剛度：

考慮扣件橫向剛度可變，在保持其他參數(shù)不變的情況下，分別將鋼軌扣件橫向剛度取值2 kN/mm、5 kN/mm、10 kN/mm、15 kN/mm 和20 kN/mm 五種情況，計(jì)算分析鋼軌跨中簡(jiǎn)諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的橫向?qū)Ъ{，如圖10所示。

由圖10可知，改變鋼彈簧浮置板軌道的扣件橫向剛度，主要會(huì)影響鋼軌在0～700 Hz 頻率范圍內(nèi)的橫向振動(dòng)特性。在1 Hz～300 Hz范圍內(nèi)扣件橫向剛度越大，其鋼軌導(dǎo)納幅值有所下降，主頻峰值也朝高頻移動(dòng)。在300 Hz～700 Hz 范圍內(nèi)，導(dǎo)納峰值出現(xiàn)周期性波動(dòng)，但總體上呈現(xiàn)出隨著扣件橫向剛度增大，導(dǎo)納幅值有降低的趨勢(shì)，364 Hz處于扣件橫向剛度15 kN/mm對(duì)應(yīng)的第三個(gè)峰值上。

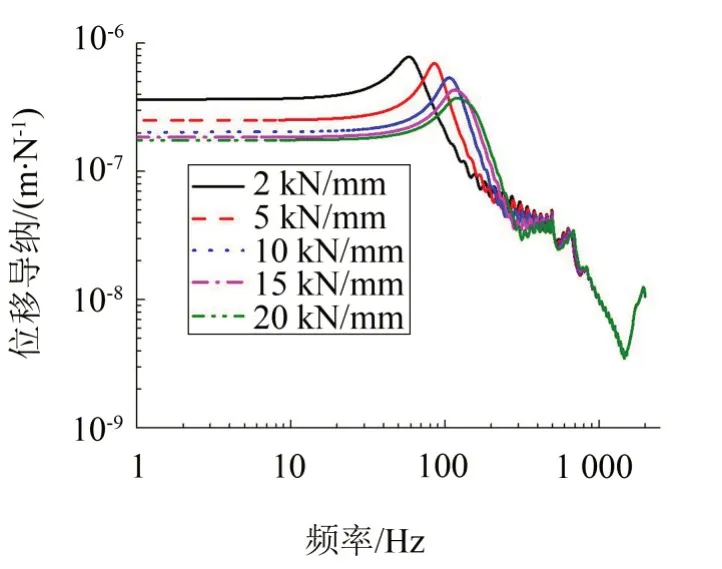
圖10 扣件橫向剛度對(duì)鋼軌橫向?qū)Ъ{的影響

3.3 隔振器剛度的影響分析

（1）隔振器垂向剛度：

地鐵中常見(jiàn)的浮置板隔振器鋼彈簧垂向剛度有5 kN/mm、6.5 kN/mm 和8 kN/mm 等，為了使浮置板隔振器研究范圍更具一般性，分別將鋼彈簧垂向剛度取值5 kN/mm、10 kN/mm和15 kN/mm 三種情況，計(jì)算分析了跨中簡(jiǎn)諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的垂向?qū)Ъ{，如圖11所示。

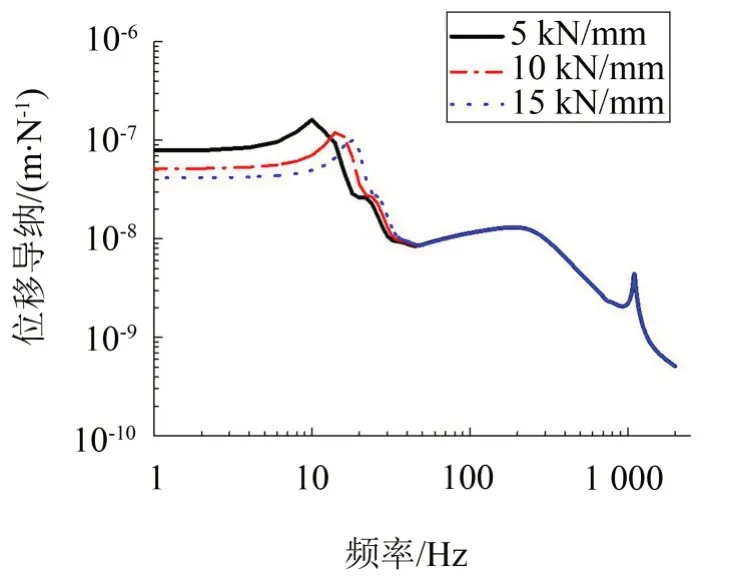
圖11 鋼彈簧垂向剛度對(duì)垂向?qū)Ъ{的影響

由圖11可知，改變鋼彈簧浮置板軌道系統(tǒng)的隔振器垂向剛度，只影響鋼軌在0～50 Hz頻率范圍內(nèi)的垂向振動(dòng)特性，而不會(huì)影響50 Hz 以上頻段的鋼軌1 階起跳共振和1 階pinned-pinned 振動(dòng)。鋼軌在10 Hz附近的導(dǎo)納變化較為明顯，隨著鋼彈簧垂向剛度由5 kN/mm逐漸增大到15 kN/mm，振動(dòng)峰值頻率從10 Hz 增大到18 Hz，對(duì)應(yīng)導(dǎo)納峰值從1.62×10-7m/N減小到9.97×10-8m/N，可見(jiàn)，隨著浮置板隔振器垂向剛度會(huì)增大，第1階振動(dòng)頻率向更高頻移動(dòng)，對(duì)應(yīng)的振動(dòng)峰值有所降低。

（2）隔振器橫向剛度：

同樣原理，在保持其他參數(shù)不變的情況下，分別取隔振器鋼彈簧橫向剛度為5 kN/mm、10 kN/mm和15 kN/mm 三種，計(jì)算跨中簡(jiǎn)諧力激勵(lì)下激勵(lì)點(diǎn)處鋼軌的橫向?qū)Ъ{，如圖12所示。

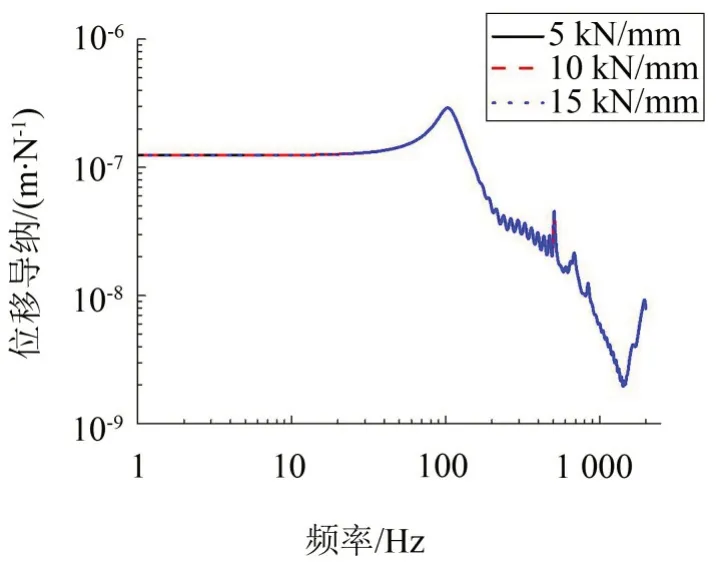
圖12 鋼彈簧橫向剛度對(duì)鋼軌橫向?qū)Ъ{的影響

由圖12可知，鋼彈簧的橫向剛度變化對(duì)鋼軌橫向?qū)Ъ{沒(méi)有影響，不會(huì)影響鋼軌振動(dòng)的特征頻率和對(duì)應(yīng)振型。

3.4 輪對(duì)模態(tài)的影響分析

結(jié)合輪對(duì)模態(tài)分析結(jié)果，其中在列車運(yùn)行過(guò)程中容易發(fā)生劇烈的輪軌共振的頻率分別有262 Hz、358 Hz、402 Hz 和474 Hz，其中頻率為358 Hz 的輪軌振動(dòng)模態(tài)，如圖13所示。

圖13 軌道和輪對(duì)共振模態(tài)

由圖13可知，358 Hz頻率下鋼軌和輪對(duì)的振動(dòng)形態(tài)以橫向振動(dòng)為主。由前面浮置板地段的波磨現(xiàn)場(chǎng)實(shí)測(cè)數(shù)據(jù)可知，存在兩個(gè)波磨特征波長(zhǎng)，分別為31.7 mm和200 mm。由于測(cè)試曲線軌道區(qū)段列車實(shí)際運(yùn)營(yíng)車速為42 km/h，根據(jù)波磨波長(zhǎng)31.7 mm計(jì)算其對(duì)應(yīng)頻率為364 Hz。考慮到實(shí)際運(yùn)營(yíng)過(guò)程中的車輛輪對(duì)附加質(zhì)量，相同振動(dòng)形態(tài)下輪軌系統(tǒng)的動(dòng)力響應(yīng)頻率應(yīng)略低于軌道系統(tǒng)本身在外界單獨(dú)激勵(lì)下的振動(dòng)頻率，則此段測(cè)試線路的短波波磨對(duì)應(yīng)的鋼軌振動(dòng)頻率為358 Hz。因此，鋼軌橫向彎曲變形頻率在358 Hz 時(shí)與此區(qū)段線路產(chǎn)生特征波長(zhǎng)為31.7 mm 波磨引起的輪軌振動(dòng)頻率較為接近。由此可見(jiàn)，可通過(guò)采取減振措施來(lái)抑制輪軌系統(tǒng)在358 Hz處的橫向振動(dòng)響應(yīng)，從而相應(yīng)地減緩鋼軌磨耗。

4 結(jié)語(yǔ)

通過(guò)對(duì)鋼彈簧浮置板區(qū)段現(xiàn)場(chǎng)波磨測(cè)試分析，建立輪對(duì)-鋼彈簧浮置板軌道三維有限元模型，進(jìn)行了模態(tài)分析和導(dǎo)納分析，探討了鋼軌扣件剛度、浮置板隔振器剛度與輪對(duì)振動(dòng)模態(tài)對(duì)鋼彈簧浮置板區(qū)段鋼軌波磨的影響規(guī)律，得到以下結(jié)論：

（1）選取的特定浮置板軌道區(qū)段的現(xiàn)場(chǎng)波磨測(cè)試結(jié)果表明，鋼彈簧浮置板區(qū)段波磨主要發(fā)生在曲線內(nèi)軌上，波長(zhǎng)約為31.7 mm，列車在波磨區(qū)段的通過(guò)頻率約為364 Hz。

（2）鋼軌扣件剛度對(duì)鋼軌振動(dòng)有重要的影響。鋼軌扣件剛度越低，將激發(fā)鋼軌較大的振動(dòng)，在特定頻段上過(guò)大的鋼軌振動(dòng)會(huì)導(dǎo)致對(duì)應(yīng)波長(zhǎng)的波磨加劇，進(jìn)而加速波磨的發(fā)展。

（3）從輪軌系統(tǒng)模態(tài)分析可知，358 Hz 的鋼軌橫向彎曲變形頻率與測(cè)試線路產(chǎn)生特征波長(zhǎng)為31.7 mm波磨引起的輪軌振動(dòng)頻率較為接近。可通過(guò)采取減振措施來(lái)抑制輪軌系統(tǒng)在358 Hz 處的橫向振動(dòng)響應(yīng)，從而相應(yīng)地減緩鋼軌磨耗。