用加窗插值法抑制振動(dòng)信號(hào)工頻噪聲

張曉濤，李偉光

（1.廣東機(jī)電職業(yè)技術(shù)學(xué)院汽車學(xué)院, 廣州 510515；2.華南理工大學(xué)機(jī)械與汽車工程學(xué)院, 廣州 510640）

可傾瓦軸承因各油楔的壓力總是指向轉(zhuǎn)軸中心而形成最佳油膜，具有能承受各方向徑向載荷、高速旋轉(zhuǎn)穩(wěn)定性好、承載能力大等優(yōu)點(diǎn)，被廣泛用于大型汽輪機(jī)、燃?xì)廨啓C(jī)、風(fēng)機(jī)、泵等旋轉(zhuǎn)機(jī)械。采用電渦流位移傳感器采集可傾瓦軸承的振動(dòng)信號(hào)，耦合到振動(dòng)信號(hào)的工頻噪聲對(duì)振動(dòng)特征分析產(chǎn)生影響，因而需要研究有效的工頻噪聲抑制方法。

工頻噪聲抑制是重要研究課題。工頻噪聲實(shí)際上是來(lái)自電力系統(tǒng)的工頻基波及其諧波，工頻基波不是恒定不變的，而是在50 Hz 上下有小幅波動(dòng)。為抑制工頻噪聲國(guó)內(nèi)外學(xué)者提出了諸多方法，按基本原理主要可分為六類[1]，基于濾波器理論的方法[2]、基于盲源分離的方法[3]、基于神經(jīng)網(wǎng)絡(luò)的方法[4]、基于參數(shù)擬合的方法[5]、基于信號(hào)分解的方法[6]、基于奇異值分解的方法[7]等。這些方法在特定條件下效果明顯，但又存在一定的局限性，如基于濾波器理論的方法要求工頻頻率為恒定的50 Hz，顯然這與實(shí)際情況不符，因而該方法既抑制了工頻噪聲同時(shí)也會(huì)損害了有用信號(hào)。

工頻噪聲來(lái)自電力系統(tǒng)，可將電力信號(hào)的分析方法擴(kuò)展到振動(dòng)信號(hào)領(lǐng)域，用于振動(dòng)信號(hào)的工頻噪聲抑制，其中加窗插值法[8]是常見(jiàn)的電力信號(hào)分析方法。電力信號(hào)主要包含基波、二次諧波、三次諧波等高次諧波及間諧波，加窗插值法用于計(jì)算各次諧波的參數(shù)（幅值、頻率和相位）。通常電力信號(hào)的高次諧波比較微弱，故可以忽略。電力信號(hào)各成分的頻譜間距比較大，而受工頻噪聲干擾的振動(dòng)信號(hào)的成分則復(fù)雜得多，振動(dòng)信號(hào)中既包含有用信號(hào)成分也包含工頻噪聲，有用信號(hào)成分頻譜與工頻噪聲頻譜的間距不確定，甚至?xí)丿B在一起。加窗插值法應(yīng)用時(shí)既要考慮窗函數(shù)特性也要考慮被分析信號(hào)特點(diǎn)[9]。因信號(hào)特征不同，用于電力信號(hào)的加窗插值法不能直接照搬到振動(dòng)信號(hào)，加窗插值法用于振動(dòng)信號(hào)分析雖具有可行性，但相關(guān)研究報(bào)道并不多見(jiàn)。張營(yíng)等[6]用譜插值法消除工頻成分，譜插值法就是將時(shí)域插值方法應(yīng)用于頻域分析，具體做法是先對(duì)信號(hào)作快速傅里葉變換（Fast Fourier Transform，F(xiàn)FT），并將對(duì)應(yīng)于工頻50 Hz 的單一譜線去掉，用相鄰的兩個(gè)頻譜值對(duì)其作線性內(nèi)插以得到新值，并用新值替換原值，最后作逆傅里葉變換（Ⅰnverse Fast Fourier Transform，ⅠFFT），得到消除工頻噪聲的信號(hào)。但筆者認(rèn)為該做法值得商榷，因?yàn)閷⒐ゎl噪聲簡(jiǎn)化為一根譜線是不準(zhǔn)確的。

本文先仿真分析信號(hào)加不同窗函數(shù)時(shí)的工頻插值計(jì)算結(jié)果，進(jìn)而對(duì)實(shí)測(cè)振動(dòng)信號(hào)進(jìn)行加窗插值分析，最終選用合適的窗函數(shù)以打我的最準(zhǔn)確的插值計(jì)算結(jié)果，即使得工頻噪聲的抑制效果最好。

1 加窗插值法分析

所謂加窗插值法就是先對(duì)信號(hào)加窗函數(shù)，再對(duì)相鄰的若干條頻譜線應(yīng)用插值公式，計(jì)算出信號(hào)的頻率、幅值和相位。按照所用譜線數(shù)的不同，插值方法可分為雙譜線插值[8]、三譜線插值[10]、四譜線插值[11]等，本文采用雙譜線插值。加窗插值法用于振動(dòng)信號(hào)分析，首先要選取合適的窗函數(shù)。窗函數(shù)種類較多，大體可分為冪窗、三角函數(shù)窗和指數(shù)窗三類，每一類又含有多種窗函數(shù)。各窗函數(shù)的主要區(qū)別是主瓣寬度、旁瓣峰值和旁瓣衰減速度，窗函數(shù)的選擇就是依據(jù)這三項(xiàng)指標(biāo)。矩形窗是最簡(jiǎn)單形式的冪窗，通常不加窗就是加了矩形窗，而漢寧窗和六項(xiàng)余弦窗都是余弦窗。矩形窗、漢寧窗和六項(xiàng)余弦窗三種窗函數(shù)的項(xiàng)數(shù)和系數(shù)不同[12]，使得各窗函數(shù)的頻譜特征差別很大，如圖1 所示，矩形窗主瓣窄、旁瓣多且旁瓣衰減慢，六項(xiàng)余弦窗主瓣寬、旁瓣窄且旁瓣衰減快，而漢寧窗的主瓣及旁瓣特征位于矩形窗和六項(xiàng)余弦窗之間。矩形窗、漢寧窗和六項(xiàng)余弦窗的主瓣寬度、旁瓣峰值、旁瓣衰減速度的具體數(shù)值分dB/octave；24 π/N、-88 dB、-66 dB/octave。三種窗函數(shù)具有特征完全不同的主瓣和旁瓣，因而能夠比較全面地反映窗函數(shù)這一類對(duì)象。

周期信號(hào)加窗函數(shù)并作FFT 后，可由主瓣上相鄰的兩個(gè)譜峰經(jīng)插值公式[13-14]計(jì)算出其參數(shù)（幅值、頻率、相位）。若周期信號(hào)用x0（n）（n=0,1,···,N-1）表示，采樣頻率用fs表示，采樣間隔用T表示，則。用窗函數(shù)w（n）對(duì)x0（n）作N點(diǎn)截?cái)啵秒x散信號(hào)序列x（n）：

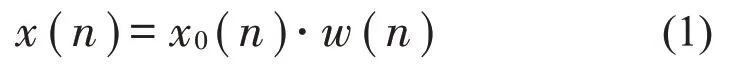
對(duì)x（n）作FFT，分別用hm、fm、phase（hm）表示主瓣上左側(cè)譜線的幅值、頻率、相位，分別用hm+1和fm+1表示右側(cè)譜線的幅值、頻率。待計(jì)算的頻率、幅值、相位分別用f、A、θ表示。

當(dāng)信號(hào)加矩形窗時(shí)，令插值系數(shù)δ為：

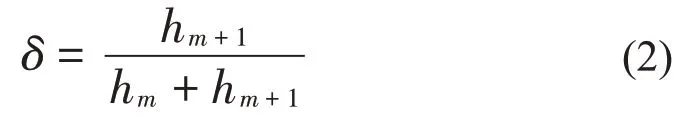
插值公式為：

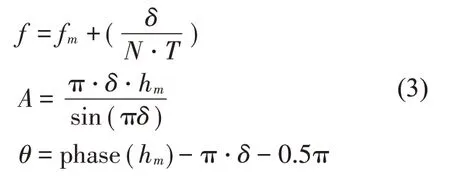
當(dāng)信號(hào)加漢寧窗時(shí)，令插值系數(shù)δ為：

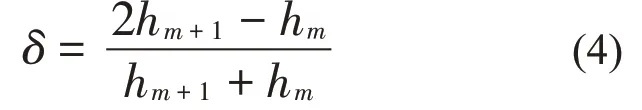
插值公式為：

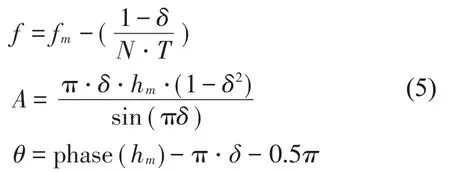
當(dāng)信號(hào)加六項(xiàng)余弦窗時(shí)，令插值系數(shù)δ為：

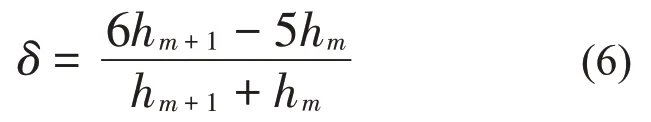
插值公式為：

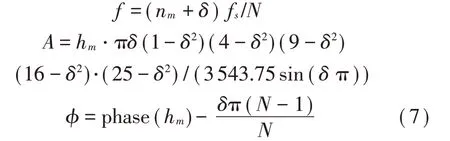
應(yīng)用加窗插值抑制法，通過(guò)上述插值公式可計(jì)算工頻噪聲參數(shù)的精確值，從而將其從信號(hào)中消除，達(dá)到工頻噪聲抑制的目的。

2 數(shù)值仿真試驗(yàn)分析

可傾瓦軸承振動(dòng)試驗(yàn)需要在不同的轉(zhuǎn)速下進(jìn)行，經(jīng)振動(dòng)傳感器采集的振動(dòng)信號(hào)的特征頻率也隨之不同，而耦合到振動(dòng)信號(hào)中的工頻噪聲的頻率則基本穩(wěn)定。應(yīng)用數(shù)值仿真方法對(duì)此工況進(jìn)行模擬，并針對(duì)仿真信號(hào)研究合適的窗函數(shù)，以使經(jīng)插值公式計(jì)算得到的工頻參數(shù)最準(zhǔn)確。雖然在實(shí)際試驗(yàn)過(guò)程中振動(dòng)信號(hào)的振動(dòng)分量和工頻噪聲分量的參數(shù)都是變化的，但此處為便于仿真分析，將工頻噪聲分量的參數(shù)設(shè)為某一定值，振動(dòng)分量的幅值和相位也設(shè)為定值，而只改變振動(dòng)分量的頻率。

仿真信號(hào)用x（t）表示，如公式（8）所示，包括表征工頻噪聲的分量x1（t），表征振動(dòng)特征的分量x2（t），及高斯白噪聲ξ（t），信噪比為30 dB。

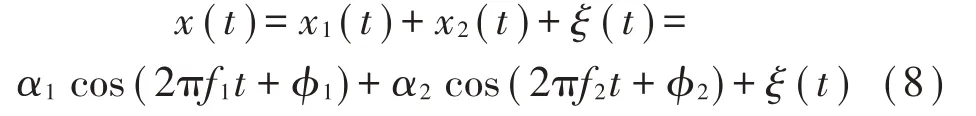
設(shè)x1（t）分量參數(shù)為：α1=2，f1=50.2 Hz，?1=π/18。設(shè)x2（t）分量的幅值和相位為：α2=1，?2=7π/9，每次試驗(yàn)時(shí)頻率f2取不同的值，f2值取為：30、33、35、38、40、41、42、43、44、45、46、47、48、49、51、52、53、54、55、56、57、58、59、60、62、65、68、70，共28 個(gè)值，單位為Hz。當(dāng)f2=30 Hz時(shí)，仿真信號(hào)x（t）的波形如圖2所示。

圖2 仿真信號(hào)波形（當(dāng)f2 為30 Hz時(shí)）

按以上方法可生成28個(gè)仿真信號(hào)，每個(gè)仿真信號(hào)分別加矩形窗、漢寧窗、六項(xiàng)余弦窗，再用插值公式（3）、式（5）、式（7）計(jì)算x1（t）的參數(shù)（幅值、頻率、相位）。當(dāng)圖2 所示仿真信號(hào)，加矩形窗時(shí)計(jì)算的幅值、頻率、相位分別為：2.001 296、50.502 924、9.732 154，誤差分別為：0.064 814%、0.005 791%、2.678 465%；加漢寧窗時(shí)計(jì)算的幅值、頻率、相位分別為：2.002 086、50.500 167、10.155 155，誤差分別為：0.104 282%、0.000 331%、1.551 547%；加六項(xiàng)余弦窗時(shí)計(jì)算的幅值、頻率、相位分別為：1.997 974、50.503 487、9.528 856，誤差分別為：0.101 276 %、0.006 906%、4.711 439%。無(wú)論加哪種窗函數(shù)，由加窗插值法計(jì)算的工頻參數(shù)的誤差都很小，參數(shù)值非常準(zhǔn)確。進(jìn)一步地，將28 個(gè)仿真信號(hào)的工頻分量x1（t）的幅值誤差繪制為圖3（a），頻率誤差繪制為圖3（b），將相位誤差繪制為圖3（c）。由圖3 可見(jiàn)，在48 Hz～53 Hz頻率范圍內(nèi)，信號(hào)加矩形窗時(shí)x1（t）參數(shù)的誤差最小，加六項(xiàng)余弦窗時(shí)x1（t）參數(shù)的誤差最大，而加漢寧窗時(shí)的x1（t）參數(shù)的誤差則位于兩者之間。

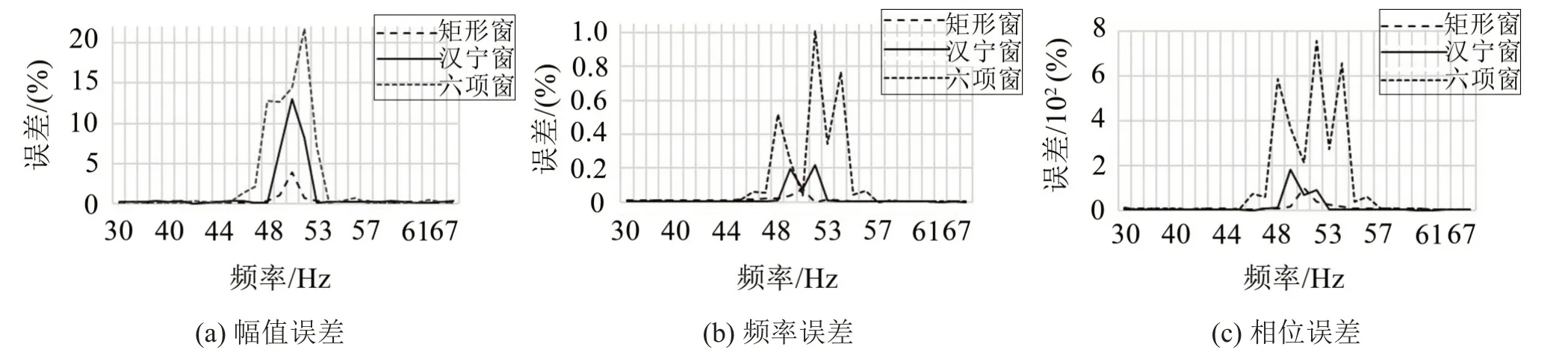
圖3 加不同窗函數(shù)時(shí)工頻參數(shù)誤差

圖3 中當(dāng)超出48 Hz～53 Hz 頻率范圍時(shí)，因?yàn)榧硬煌昂瘮?shù)時(shí)的x1（t）參數(shù)的誤差值都比較小，三者完全重疊在一起而難以分辨。進(jìn)一步地，將縱軸數(shù)值最低的部分區(qū)域放大，圖3（a）放大為圖4（a），圖3（b）放大為圖4（b），圖3（c）放大為圖4（c）。由圖4可更清晰地區(qū)分開(kāi)加不同窗函數(shù)時(shí)x1（t）參數(shù)的計(jì)算誤差。在圖4（a）中，信號(hào)分別加三個(gè)窗函數(shù)時(shí)幅值誤差都有較大波動(dòng)，三者間沒(méi)有明顯區(qū)分；在圖4（b）中，信號(hào)加矩形窗時(shí)頻率誤差最大，加六項(xiàng)余弦窗時(shí)頻率誤差次之，而加漢寧窗時(shí)頻率誤差最小；在圖4（c）中，信號(hào)加矩形窗和六項(xiàng)余弦窗時(shí)相位誤差波動(dòng)都比較大，而加漢寧窗時(shí)相位誤差波動(dòng)最小。就綜合性能而言，信號(hào)加漢寧窗時(shí)的工頻參數(shù)計(jì)算誤差最優(yōu)，顯然此時(shí)將工頻噪聲刪除所導(dǎo)致的誤差也最小。

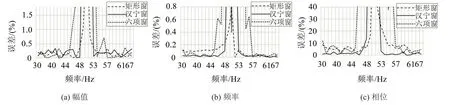
圖4 加不同窗函數(shù)時(shí)的工頻參數(shù)誤差（放大）

數(shù)值仿真試驗(yàn)結(jié)論：當(dāng)振動(dòng)信號(hào)的特征頻率位于48 Hz～53 Hz 范圍時(shí)，信號(hào)加矩形窗時(shí)工頻噪聲的抑制效果最好；當(dāng)振動(dòng)信號(hào)的特征頻率超出此范圍時(shí)，加漢寧窗時(shí)工頻噪聲的抑制效果最好。

3 實(shí)測(cè)振動(dòng)信號(hào)分析

可傾瓦軸承性能優(yōu)良、應(yīng)用廣泛，為開(kāi)發(fā)特殊應(yīng)用需求的新型可傾瓦軸承需開(kāi)展相關(guān)振動(dòng)試驗(yàn)，以使所開(kāi)發(fā)的可傾瓦軸承具有最優(yōu)的減振性能。前期項(xiàng)目已為此搭建了可傾瓦軸承轉(zhuǎn)子試驗(yàn)系統(tǒng)[7]，該系統(tǒng)示意圖如圖5 所示，系統(tǒng)包括基座、伺服電機(jī)、傳動(dòng)裝置、轉(zhuǎn)子、軸承座、轉(zhuǎn)子兩端推力軸承、稀油站、測(cè)試系統(tǒng)、控制系統(tǒng)等。在兩個(gè)軸承座的內(nèi)側(cè)固定四個(gè)支架，安裝四個(gè)Kaman 電渦流位移傳感器進(jìn)行振動(dòng)量監(jiān)測(cè)，傳感器型號(hào)為KD2306，精度為0.1 μm，頻響速度為50 kHz，安裝現(xiàn)場(chǎng)如圖6所示，圖中圓圈內(nèi)的就是電渦流位移傳感器。

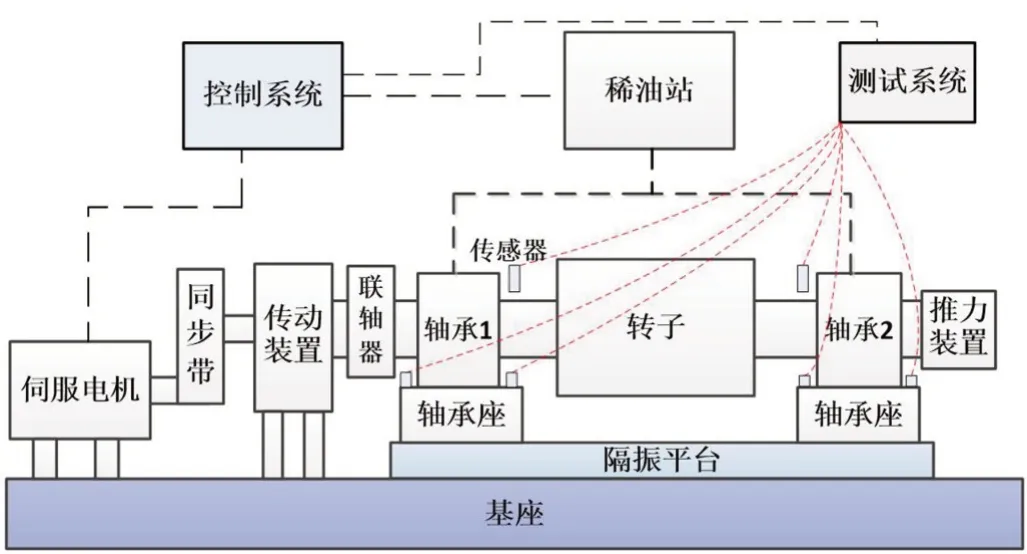
圖5 可傾瓦軸承轉(zhuǎn)子試驗(yàn)系統(tǒng)示意圖

圖6 電渦流位移傳感器安裝現(xiàn)場(chǎng)

試驗(yàn)中發(fā)現(xiàn)有電網(wǎng)工頻噪聲耦合到振動(dòng)信號(hào)，工頻噪聲對(duì)振動(dòng)信號(hào)的特征分析造成干擾，本文擬采用加窗插值法加以抑制。當(dāng)可傾瓦軸承轉(zhuǎn)子系統(tǒng)工作在轉(zhuǎn)速3 900轉(zhuǎn)/分時(shí)，即轉(zhuǎn)頻為65 Hz時(shí)系統(tǒng)工作于高速下，此時(shí)是特別需要關(guān)注的工況。若此工況下的振動(dòng)信號(hào)用x（t）表示，x（t）時(shí)域波形及頻譜如圖7所示，圖7（b）中工頻噪聲已被標(biāo)出。轉(zhuǎn)子工作頻率為65 Hz，與工頻噪聲頻率50 Hz 之間相差15 Hz，根據(jù)前面仿真試驗(yàn)結(jié)論，振動(dòng)信號(hào)加漢寧窗時(shí)工頻噪聲的抑制效果最好，為進(jìn)一步驗(yàn)證此結(jié)論，這里同時(shí)給出了加三種窗函數(shù)時(shí)的計(jì)算結(jié)果。

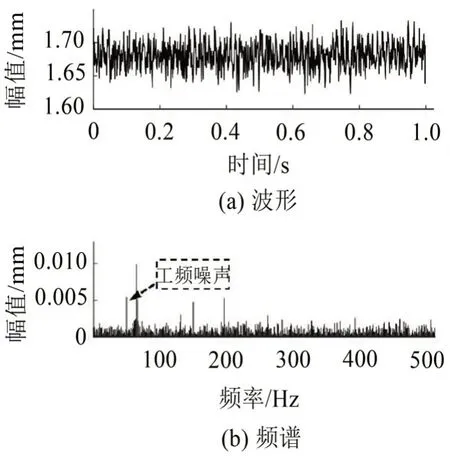
圖7 振動(dòng)信號(hào)波形及頻譜

信號(hào)x（t）分別加矩形窗、漢寧窗、六項(xiàng)余弦窗，并分別用插值公式（3）、式（5）、式（7）計(jì)算出工頻噪聲的參數(shù)，將計(jì)算結(jié)果填入表1。顯然僅從表1中的數(shù)值無(wú)法得知加哪個(gè)窗函數(shù)更合適。

若表1 中的幅值、頻率和相位分別用字母A、F和P表示，則工頻噪聲可用式（9）表示，即：

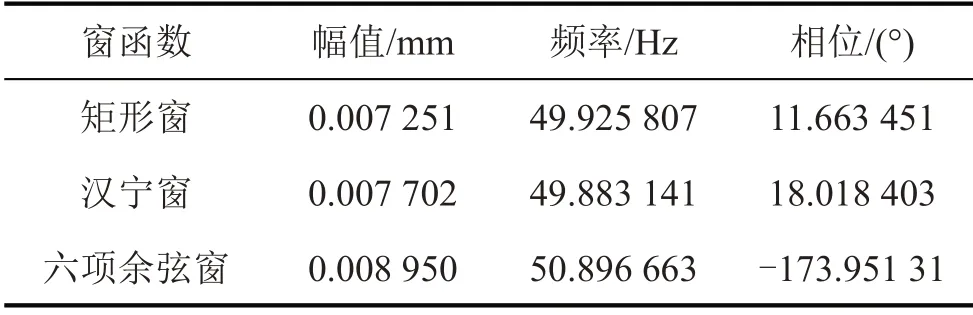
表1 振動(dòng)信號(hào)工頻噪聲參數(shù)

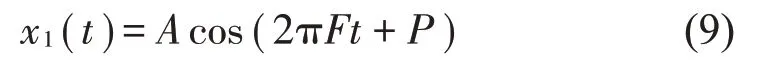
由x（t）減x1（t），可得工頻噪聲被抑制后的振動(dòng)信號(hào)x0（t），再對(duì)x0（t）作FFT，生成如圖8 所示的頻譜圖。分別將圖8（a）和圖8（b）與圖7（b）相比，發(fā)現(xiàn)工頻噪聲被有效地抑制了，而將圖8（c）與圖7（b）相比，發(fā)現(xiàn)工頻噪聲并沒(méi)有被有效抑制，這說(shuō)明加矩形窗和漢寧窗后用插值公式計(jì)算的工頻參數(shù)值比較準(zhǔn)確，而加六項(xiàng)余弦窗的插值計(jì)算結(jié)果最差。

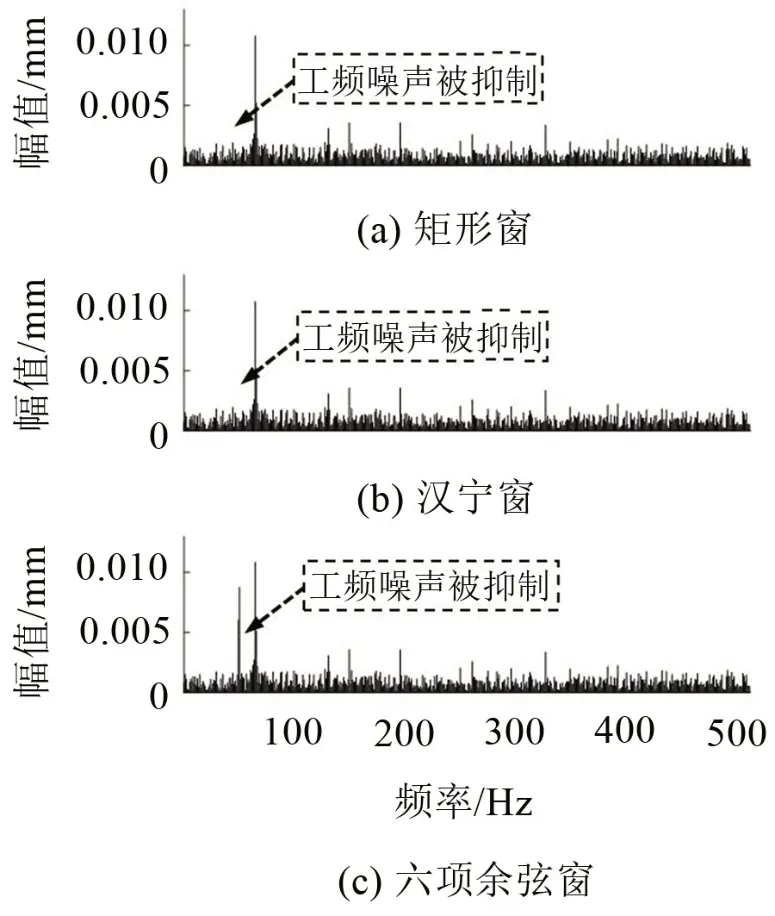
圖8 加不同窗函數(shù)時(shí)工頻噪聲被抑制的振動(dòng)信號(hào)

工頻噪聲的頻率雖然存在一定波動(dòng)，但波動(dòng)范圍很小，因?yàn)楣ゎl噪聲來(lái)源于電網(wǎng)電源，而電網(wǎng)頻率是比較穩(wěn)定的。如果多次重復(fù)采集振動(dòng)信號(hào)進(jìn)行試驗(yàn)，由加窗插值法計(jì)算的頻率參數(shù)理應(yīng)比較穩(wěn)定。基于此規(guī)律，在相同的試驗(yàn)工況和采樣率條件下另外截取七段長(zhǎng)度相同的信號(hào)，分別加矩形窗、漢寧窗、六項(xiàng)余弦窗，再用插值公式（3）、式（5）、式（7）計(jì)算工頻參數(shù)，并將8次的試驗(yàn)結(jié)果匯總到圖9。

由圖9（a）可見(jiàn)，雖然加三種窗函數(shù)時(shí)幅值參數(shù)的波動(dòng)都比較大，而其中加漢寧窗時(shí)的幅值參數(shù)的波動(dòng)略小，但三者變化趨勢(shì)基本一致，出現(xiàn)幅值波動(dòng)的原因可能主要是受現(xiàn)場(chǎng)工作環(huán)境及電網(wǎng)負(fù)荷的影響；由圖9（b）可見(jiàn)，加六項(xiàng)余弦窗時(shí)頻率參數(shù)波動(dòng)最大，加漢寧窗和矩形窗時(shí)的頻率參數(shù)則比較穩(wěn)定，其中加漢寧窗時(shí)的頻率參數(shù)的波動(dòng)更小；由圖9（c）可見(jiàn)，加六項(xiàng)余弦窗時(shí)的相位參數(shù)的波動(dòng)較大，而加漢寧窗、矩形窗的相位值雖然有波動(dòng)，但二者趨勢(shì)基本一致，由于每次試驗(yàn)的信號(hào)都是在不同時(shí)刻所采集的，因而存在相位波動(dòng)也是正常的。

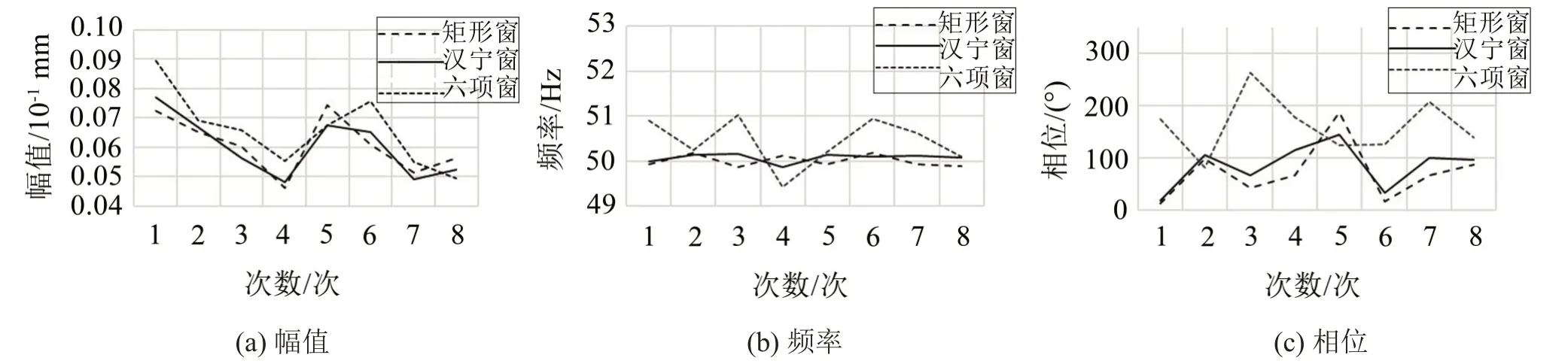
圖9 加窗插值法所提取的工頻參數(shù)

分析結(jié)果表明：加窗插值法用于實(shí)測(cè)振動(dòng)信號(hào)的工頻噪聲抑制具有可行性。雖然文中是以轉(zhuǎn)速3 900 轉(zhuǎn)/分的工況為例來(lái)分析的，但同樣也可以分析其他工況，這里受篇幅所限而不再贅述。

4 與陷波器方法對(duì)比

陷波器是常用的工頻噪聲抑制方法，由數(shù)字濾波器理論[15]可設(shè)計(jì)50 Hz陷波器，其計(jì)算式為：

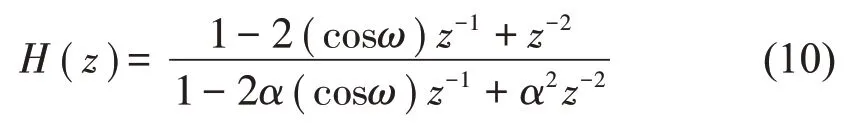
ω=2 πf/fs=0.306 6，f=50 Hz，fs為采樣率。α值確定陷波器的寬度和深度，其值越大則凹陷越深、寬度越窄。為得到最佳濾波效果，該值取為0.98。設(shè)計(jì)的陷波器頻譜如圖10所示。

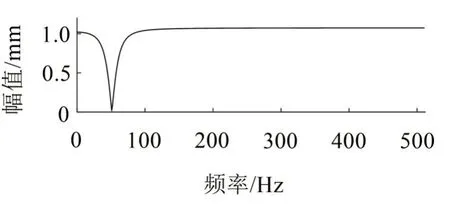
圖10 陷波器頻譜

振動(dòng)信號(hào)經(jīng)陷波器濾波后的結(jié)果如圖11所示，將其與圖8（b）相比，發(fā)現(xiàn)工頻噪聲被濾掉，同時(shí)與工頻噪聲相鄰的部分有用信號(hào)也被濾掉，從而對(duì)后續(xù)的振動(dòng)特征的量化分析產(chǎn)生影響。這表明加窗插值法同陷波器法相比具有明顯優(yōu)勢(shì)。

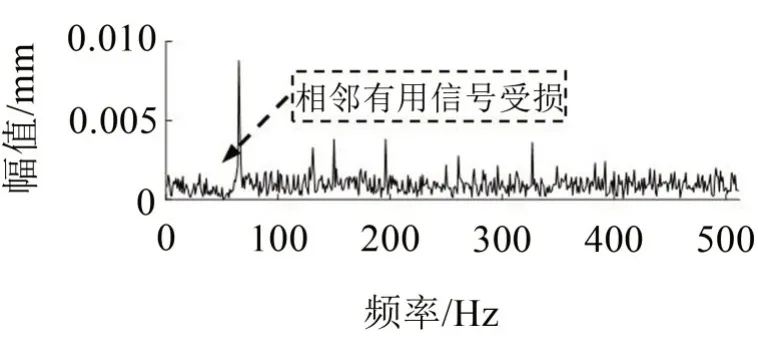
圖11 陷波器濾波后振動(dòng)信號(hào)頻譜

5 結(jié)語(yǔ)

為將加窗插值法應(yīng)用于振動(dòng)信號(hào)的工頻噪聲抑制，本文選取矩形窗、漢寧窗和六項(xiàng)余弦窗等三個(gè)典型的窗函數(shù)，并基于仿真信號(hào)和實(shí)測(cè)可傾瓦軸承振動(dòng)信號(hào)對(duì)比了加不同窗函數(shù)時(shí)的工頻插值計(jì)算結(jié)果，當(dāng)振動(dòng)信號(hào)加漢寧窗時(shí)工頻噪聲抑制效果最好，表明加窗插值法用于振動(dòng)信號(hào)工頻噪聲抑制是可行的，能較準(zhǔn)確地抑制工頻噪聲。加窗插值法從信號(hào)自身特征出發(fā)，應(yīng)用精確計(jì)算公式抑制工頻噪聲，對(duì)有用信號(hào)損害小，同傳統(tǒng)陷波器法相比具有顯著優(yōu)勢(shì)。

實(shí)際上對(duì)于理想無(wú)隨機(jī)噪聲的信號(hào)，當(dāng)其加六項(xiàng)余弦窗時(shí)工頻噪聲的插值計(jì)算結(jié)果最準(zhǔn)確，下一步將研究如何降低隨機(jī)噪聲以獲得更準(zhǔn)確的工頻參數(shù)，進(jìn)而使得抑制效果更好。窗函數(shù)眾多，如何選取更適合工頻噪聲抑制的窗函數(shù)也是后續(xù)需要研究的內(nèi)容。