基礎激勵下轉子-軸承-支座系統動力學特性研究

徐敬崗，鄧景珊，李 峰

（1.上海大學機電工程與自動化學院，上海 200444；2.常州工程職業技術學院智能制造學院，江蘇常州 213164；3.江蘇理工學院電氣信息工程學院，江蘇常州 213001）

旋轉機械廣泛應用于汽車、船舶以及航空航天等領域。一些旋轉機械，其基礎是運動的，難免會遇到外部激勵的情況。例如爆炸沖擊和波浪作用的艦船燃氣輪機，地震時地面上的旋轉機械以及行駛汽車上的傳動軸系，當前，基礎激勵下轉子系統的振動問題是學術研究的熱點方向之一。

Dakel等[1-2]通過有限元法研究了偏心質量和基礎運動耦合作用對軸系臨界轉速和軸心軌跡的影響規律。Duchemin等[3]通過理論和實驗綜合研究了軸系在臨界轉速附近時基礎運動對系統穩定性的影響規律。Fawzi 等[4]分別研究了線性和非線性支承下基礎激勵對轉子耦合系統動力學響應的影響規律。Edwards 等[5]通過試驗分析了柔性轉子系統在基礎激勵下的動態特性，獲得了基礎激勵參數對系統響應的影響規律。Yan 等[6]選取了Jeffcott 轉子系統為研究對象，考慮了基礎位移載荷，通過集中質量法研究了轉子系統的動力學響應特性。顏文忠等[7]基于轉子-支撐-基礎系統試驗裝置，研究了基礎振動幅值和頻率對轉子橫向振動行為的影響規律。祝長生[8]通過帶有主動電磁軸承轉子試驗臺，研究了電磁軸承基礎振動對電轉子系統動力學特性的影響規律。張歡[9]基于有限元法分別研究了基礎簡諧轉動、橫向簡諧運動、基礎沖擊激勵對轉子系統動力學響應的影響規律。倪德等[10]研究了直升機在非慣性坐標系下尾傳動軸的橫向彎曲振動特性。Wang 等[11]在基礎上施加地震波和正弦激勵，研究了水平轉子系統在基礎激勵下的非線性動態響應。綜上所述，目前國內針對轉子系統基礎振動問題進行了較多研究，但動力學模型一般都較為簡單，對于綜合考慮柔性轉軸、非線性滾動軸承效應以及支座耦合系統的振動特性以及基礎振動對系統影響的研究尚不多見。

本研究綜合考慮滾動軸承非線性彈性支承效應、滾動軸承和阻尼環之間的耦合效應、阻尼環與軸承座之間的耦合效應，建立起基礎激勵下轉子系統的耦合動力學模型。并通過數值方法分析了基礎激勵對系統動力學行為的影響規律；在此基礎上，以轉子振動位移最小為目標，對支承阻尼環的剛度系數和損耗因子進行優化設計，以減小基礎激勵對系統動力學特性的影響。

1 數學模型

本研究的轉子軸承系統主要由轉軸、滾動軸承、滾動軸承外的橡膠阻尼環、軸承座組成，其中支座固定在基礎上，系統三維模型如圖1 所示。對模型簡化，構建其力學模型，如圖2所示。假設滾動軸承和橡膠阻尼環均周向對稱。mbw1和mbwr分別為左右軸承外圈質量；mbs1和mbsr分別為左右支座質量；kx1和ky1分別表示水平和豎直方向支座與基礎之間的剛度，cx1和cy1分別表示相應方向上支座與基礎之間的阻尼。

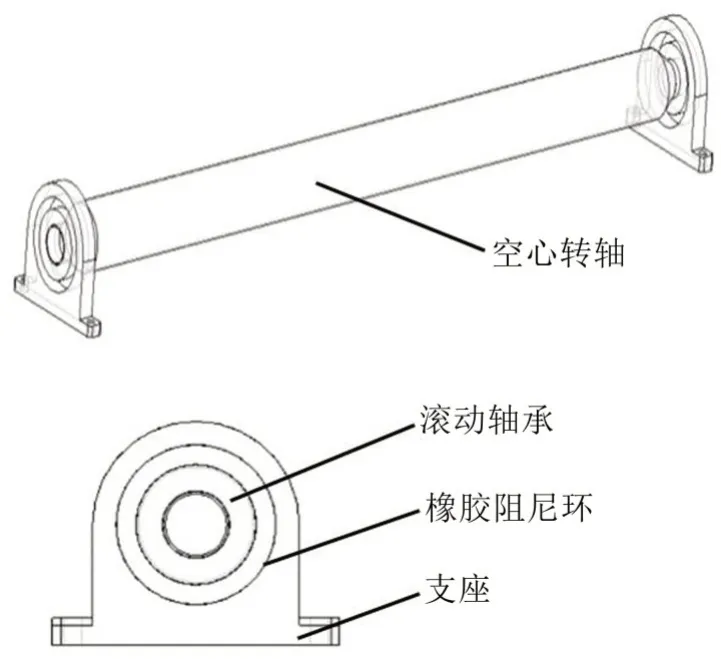
圖1 系統物理模型

圖2 系統力學模型

2 系統方程組

2.1 轉軸系統動力學方程

轉軸采用Timoshenko 梁單元建立其有限元模型，主要考慮橫向振動，每個節點具有四個自由度。根據文獻[12-13]，可以求得轉軸單元質量矩陣Me、剛度矩陣Ke、陀螺矩陣Ge和重力矩陣Qe；阻尼采用瑞雷阻尼，即Ce=αMe+βKe。

滾動軸承滾動體數為N，轉軸角速度為ω?，軸承外圈和內圈半徑分別為R和r。根據滾動軸承的運動學定理可得滾動體的角速度ωcage：

滾動軸承旋轉時，即使是新軸承也會產生振動。因為軸承在受到徑向載荷時，滾珠載荷是軸承外圈角位移的函數，同時軸承的總剛度連續變化，從而導致VC振動現象[14]，即：

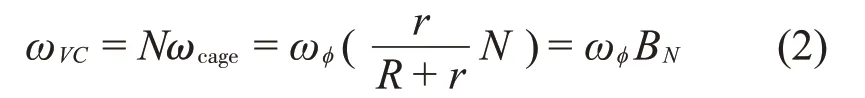
式中：BN為VC振動頻率與轉頻的比值。

假設xw1（t）、yw1（t）、xwr（t）和ywr（t）為左、右端滾動軸承外圈在x和y方向橫向振動位移，Fkxb1、Fkyb1、Fkxbr和Fkybr分別為左、右端軸承對滾動軸承外圈在x和y方向的作用力。令x=xr（0,t）-xw1、y=yr（0,t）-yw1，可求得左端軸承力Fkxb1=Fkxb、Fkyb1=Fkyb；令x=xr（L,t）-xwr、y=yr（L,t）-ywr，可求得右端軸承力Fkxbr=Fkxb、Fkybr=Fkyb。

轉軸受到的非線性軸承力包括非線性彈性力和線性阻尼力，即：

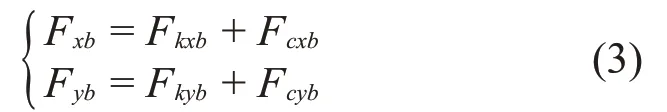
式中：

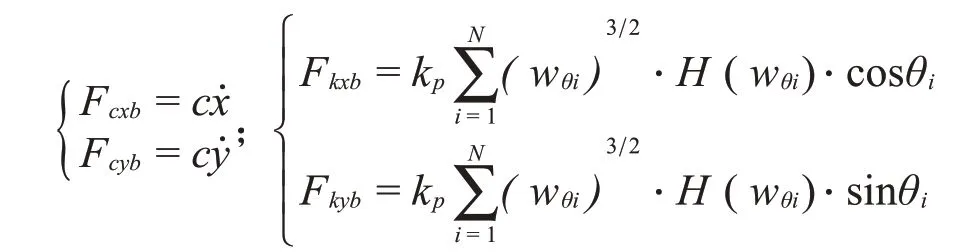
其中：kp為接觸剛度；H為亥維塞函數，視滾珠與滾道的法向接觸變形量wθi之正負而取1 或0，wθi表征了軸承游隙所引起的分段非線性，可以表示為：

將轉軸各個梁單元進行組裝，并將滾動軸承力集成到相應的節點上，即：

式中：[Mr]、[Cr]、[Kr]和[Gr]分別為轉軸質量矩陣、阻尼、剛度和陀螺矩陣；[Qr]為轉軸外力向量；Fb為相應節點的滾動軸承力。

2.2 軸承外圈動力學方程

本文采用Kelvin-Voigt 線性力學模型給出復支承度[15-16]，因此可將橡膠阻尼環的復支承力Fs表示為：

式中：k*和u分別為橡膠阻尼環的復支撐剛度和振動位移，η為橡膠阻尼環的損耗因子。

不計橡膠阻尼環振子的小轉角位移，則振動位移可表示為:u=x*+iy*，則：

式中：x*和y*為阻尼環在水平和垂直方向變形。

分析可知，軸承外圈受到滾動軸承的反作用力和阻尼環的作用力。假設左、右端支座在X方向和Y方向橫向振動位移變量分別為xbl（t）、ybl（t）、xbr（t）和ybr（t）；Fxsl、Fys;、Fxsr和Frlr分別為左、右端橡膠阻尼環對滾動軸承外圈在相應方向的作用力。基于牛頓第二定理，軸承外圈的運動微分方程組為：

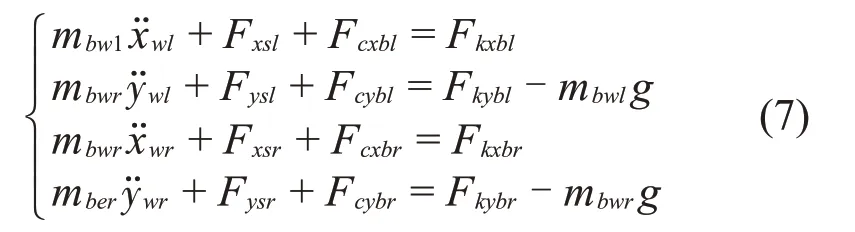
式中：

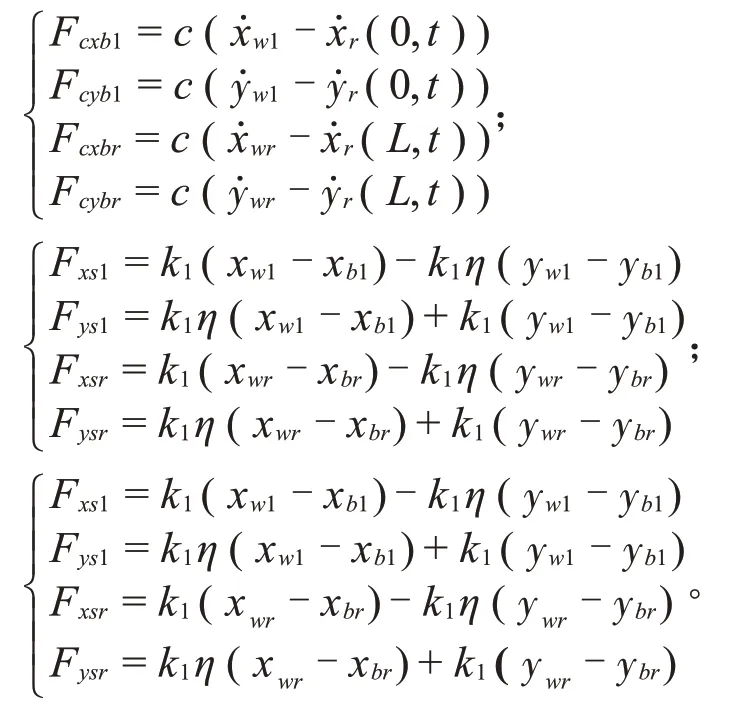
2.3 支座動力學方程

支座受到阻尼環的反作用力、與基礎之間的彈性力和阻尼力、基礎的激勵作用。假設xs（t）和ys（t）為基礎同時對左右支座在X和Y方向上的位移激勵。通過牛頓第二定理，支座的運動微分方程組為：

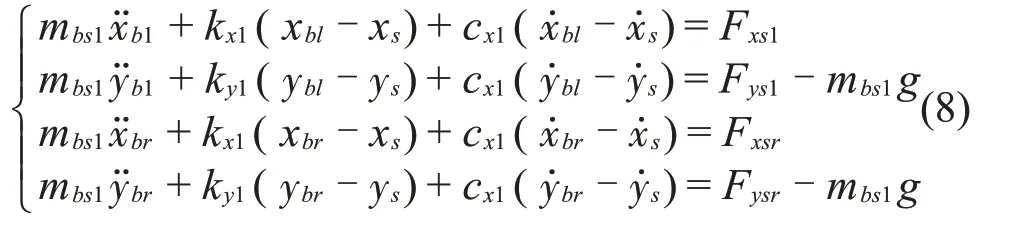
如果基礎固定不動，即xs（t）=ys（t）=0。

2.4 系統動力學方程組

結合方程組式（4）、式（7）和式（8）可以建立轉軸-滾動軸承-阻尼環-支座耦合動力學方程：

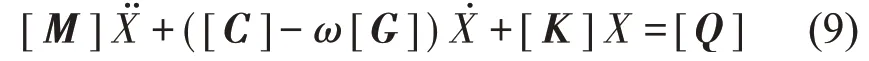
式中：[M]、[C]、[K]和[G]為耦合系統質量、阻尼、剛度和陀螺矩陣；[Q]為耦合系統廣義力矩陣。

為保證計算精度，對系統進行無量綱化處理。通過以下代換：

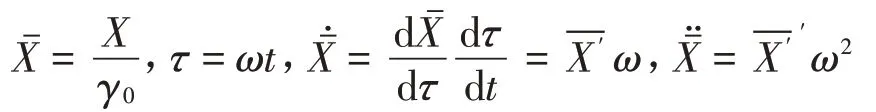
式（9）可以轉化為：

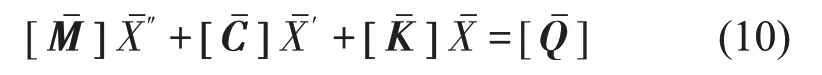
式中：[]=[M]γ0ω2，[]=（[C]-ω[G]）γ0ω，[]=[K]γ0。

3 轉子-軸承-支座耦合動力學響應分析

采用龍格-庫塔法計算耦合系統的數值解。系統動力學求解初始參數選取[16]，如下所示：

L=1m 、E=2.1×1011Pa 、μ=0.3 、ρ=7 800 kg/m3、nr=4 000 r/min 、k1=4×106N/m 、kx1=ky1=2×108N/m 、kp=7.05×109N/m32、c=1 000 N·s/m、cx1=cy1=1000 N·s/m、γ0=15 μm、r=0.006 m、R=0.01m、N=13、η=0.15、mbw1=mbwr=0.05 kg、mbs1=mbsr=0.2 kg。

3.1 無基礎振動時耦合系統動力學響應分析

無基礎振動時轉子系統安裝在固定基礎上，首先，計算獲得轉軸中心節點處振動響應隨轉速的分岔圖，如圖3 所示。分析可知，轉速在1 000 r/min～10 000 r/min 范圍內X方向中心節點的響應在Poincare 截面上存在唯一點與之對應；在轉速1 800 r/min 附近出現峰值，表明轉軸出現共振，頻率約為3.2 Hz×30 Hz=96 Hz。

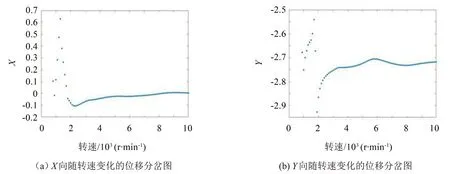
圖3 振動響應的隨轉速變化的分岔圖

為了進一步分析不同轉速下系統的運轉狀態，圖4 和圖5 分別給出了1 500 r/min 和5 000 r/min 轉速下轉軸中心節點X方向振動位移響應的時間歷程圖、相平面圖、軸心軌跡和FFT 頻譜圖。由圖可知，時間歷程圖呈現周期性的波動，相平面圖和軸心軌跡都是橢圓，頻譜圖中頻率成分為相應轉速下滾動軸承VC頻率及其諧波頻率。

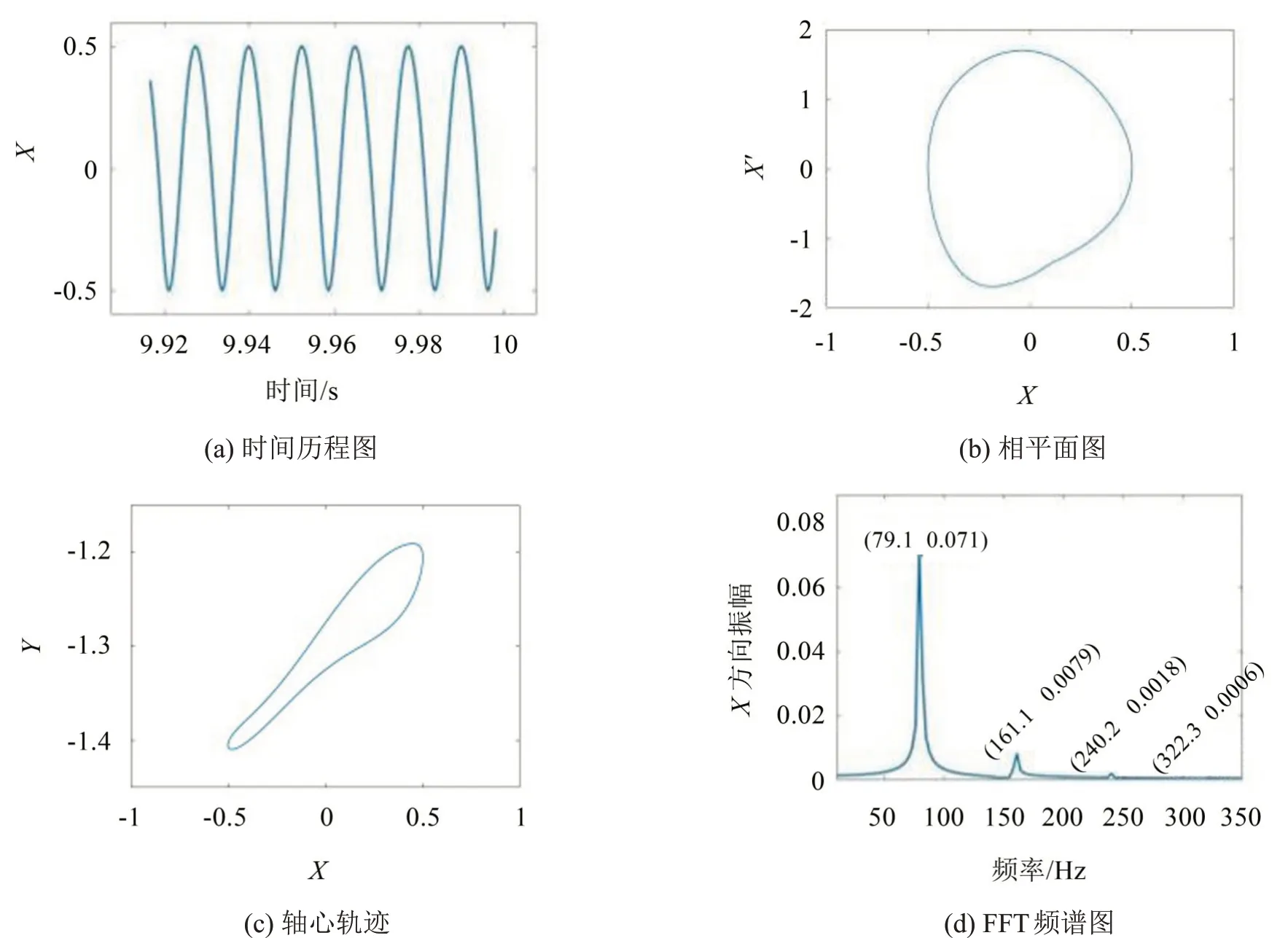
圖4 轉軸中心節點X方向上的響應（1 500 r/min）

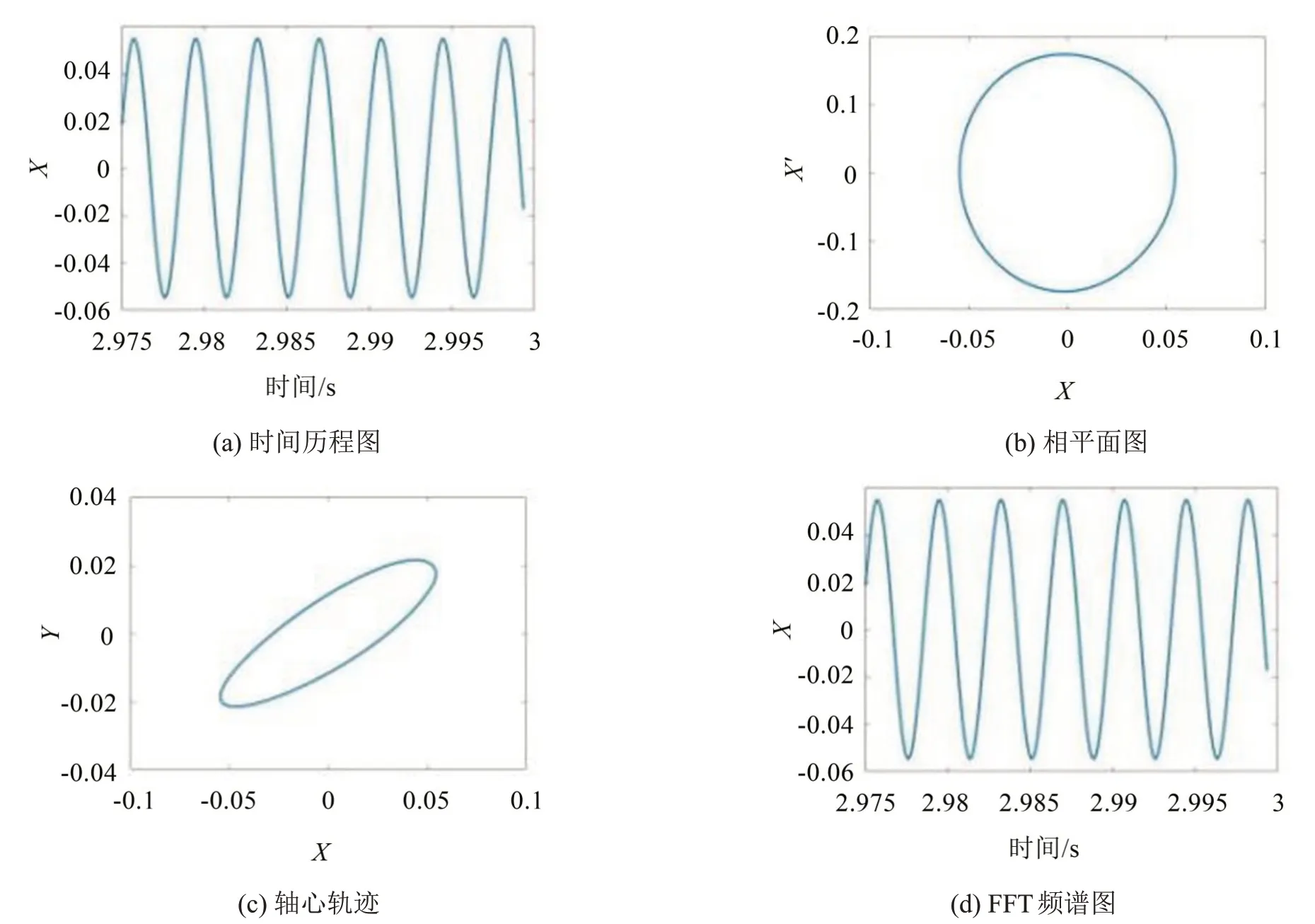
圖5 轉軸中心節點X方向上的響應（5 000 r/min）

3.2 基礎振動對耦合系統動力學特性影響分析

為研究基礎振動對耦合系統動力學特性的影響規律，取轉速1 000 r/min～8 000 r/min 范圍內，在Y向施加加速度基礎激勵（t）=Asin（Wbase*t），研究不同轉速下耦合系統的動態響應，其中A為基礎激勵幅值，Wbase為基礎運動角速度，分別取A=0.8 m/s2，Wbase=1000 rad/s，則基礎激勵相應的頻率為fbase=159.2 Hz。

（1）基礎振動對系統X方向動力學特性影響

為研究Y方向的基礎振動對耦合系統X方向振動響應的影響規律，分別求得有無基礎振動下，X方向振動響應的瀑布圖，具體如圖6所示。可知，無基礎振動時三維頻譜圖中頻率成分主要為隨轉速變化的滾動軸承VC頻率（fvc）。在低轉速時，可以觀察到明顯的諧波；有Y方向的基礎振動時，X方向隨轉速變化的頻譜圖不僅有滾動軸承VC 頻率及其諧波，在低轉速下可以觀察到明顯的基礎振動頻率成分（fbase）和新的頻率成分（f）。由于滾動軸承VC 頻率顯著大于其它頻率成分，為了清楚研究在不同轉速下轉軸的頻率成分，匯總1 500 r/min 和5 000 r/min轉速下響應的時間歷程圖、相平面圖、軸心軌跡、FFT頻譜圖進行詳細地分析，分別見圖7和圖8。

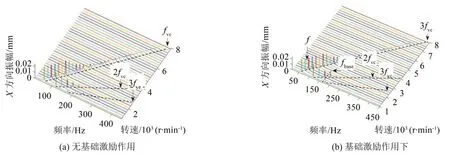
圖6 不同轉速下X方向上的振動響應的瀑布圖

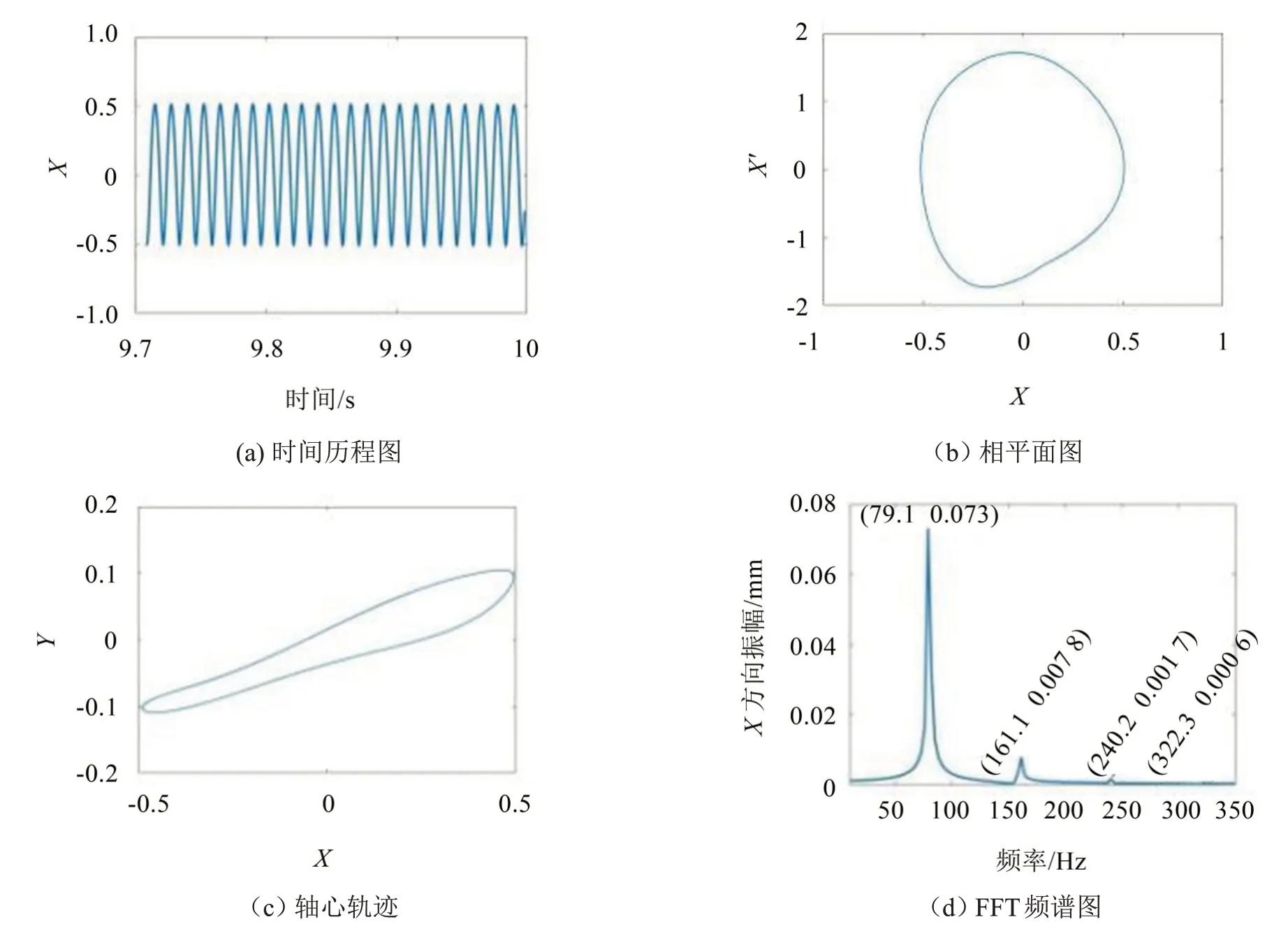
圖7 X方向上的響應（1 500 r/min）

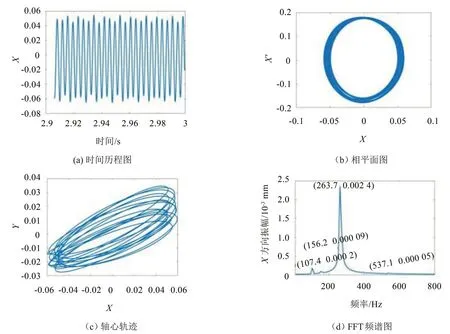
圖8 X方向上的響應（5 000 r/min）

對比圖4和圖7可知，轉速1 500 r/min下，Y方向的基礎振動不改變系統X方向的運動，響應的時間歷程圖、相平面圖、軸心軌跡大小、FFT 頻譜圖幾乎不變。此外，對比圖5 和圖8 可知，轉速5 000 r/min時，Y向的基礎振動使系統X向由周期運動變為概周期運動，軸心軌跡由穩定的橢圓變為復雜的橢圓，基礎振動下響應的頻率不僅包含滾動軸承VC 頻率（107.4 Hz）及其諧波頻率，還有基礎振動頻率（156.2 Hz）和基礎振動頻率與滾動軸承VC 頻率之差（263.7 Hz）。基礎振動下X方向不同轉速下響應的頻率成分及對應關系，具體如表1所示。

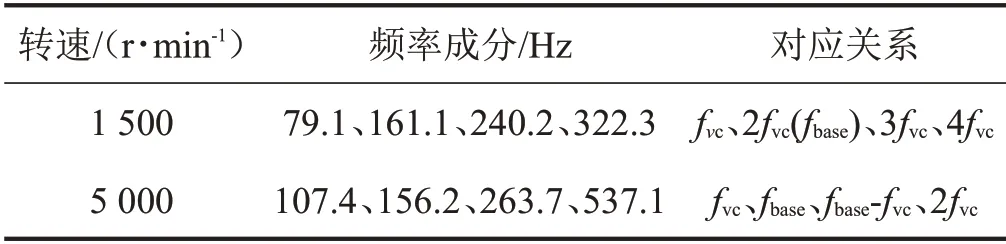
表1 轉軸中心節點在X向上頻率成分及對應關系

（2）基礎振動對Y方向動力學特性影響

同樣為了觀察Y方向基礎振動對耦合系統Y方向的影響，分別求得有無基礎振動下，Y方向振動響應的瀑布圖，具體如圖9 所示。施加加速度基礎激勵時，Y方向隨轉速變化的頻譜圖中除了滾動軸承變剛度頻率及其諧波，在整個轉速范圍內還可以觀察到明顯的基礎激勵頻率成分。

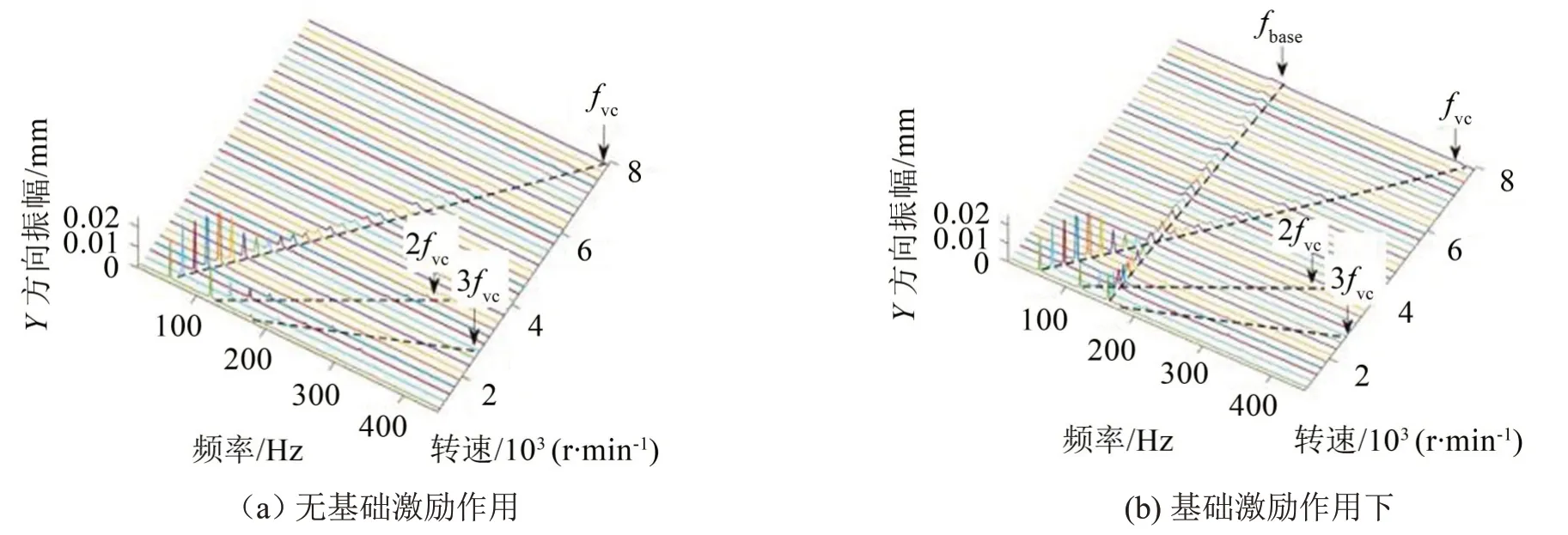
圖9 不同轉速在Y方向上的振動響應的瀑布圖

Y方向基礎振動對耦合系統Y方向的影響與對X方向影響相似，轉速1 500 r/min時，基礎振動不改變系統Y向的運動狀態；然而，轉速5 000 r/min 時，基礎振動使系統Y方向由周期運動變為概周期運動。基礎激勵下不同轉速在Y方向振動響應的頻率成分及對應關系，具體如表2所示。

表2 不同轉速下Y方向振動響應的頻率成分及對應關系

綜上所述，Y方向上基礎振動對耦合系統X和Y方向上的動力學特性都有影響。當基礎振動頻率等于滾動軸承VC 頻率或其諧波頻率時，不影響耦合系統的運動；當基礎振動頻率不等于滾動軸承VC頻率或其諧波頻率時，會呈現出組合共振現象，組合共振的頻率包括多個成分，可以表示為整數倍的滾動軸承VC頻率與基礎激勵頻率的代數和。

4 轉子軸承系統動力學參數優化設計

在設計中，要求各轉速下轉子軸承系統位移振動響應受到基礎激勵的影響盡可能減小。通過文獻[15-16]研究可知，阻尼環參數k1、η對系統動力學行為有著重要的影響。因此，本文將k1、η作為設計變量，并構建設計空間。分別1 500 r/min 和5 000 r/min轉速下X和Y方向基礎激勵對轉子振動位移幅值加權作為目標函數，通過方程式（5）、式（10）建立優化數學模型如方程式（11）：

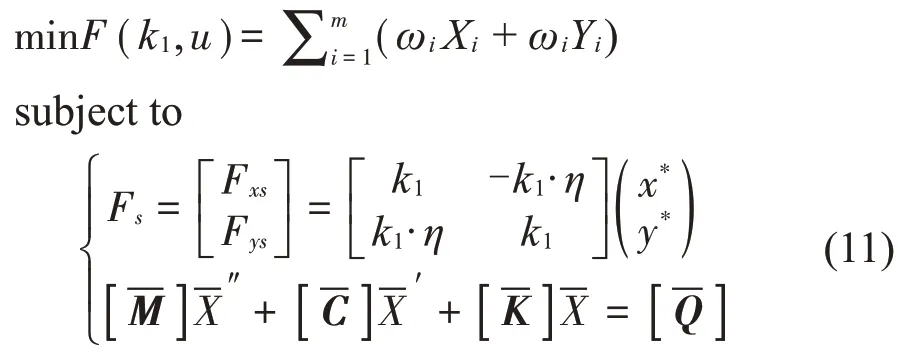
式中：ωi為權重，Xi、Yi分別為對應轉速的X和Y方向基礎激勵頻率影響下的轉軸中間節點FFT幅值。

采用遺傳算法進行優化設計，求得最優解為：

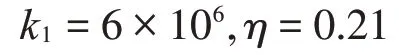
對優化后參數進行計算，獲得基礎頻率下轉軸中間節點最大幅值，可以得到表3 優化前振動響應的頻率及各方向最大幅值以及表4優化后振動頻率及各方向最大幅值的對比。

表3 優化前振動響應的頻率及幅值

表4 優化后振動響應的頻率及幅值

通過上述分析可知，在1 500 r/min 和5 000r/min 轉速下X和Y向幅值分別降低了19.72 %、20.83%及20.54%、25%。顯然，設計方法優化后，基礎激勵對轉子軸承系統的振動響應影響得到顯著減小。

5 結語

針對具有基礎激勵的轉子軸承系統，建立了轉軸-軸承-支座耦合動力學模型，模型中轉軸采用梁單元離散，考慮了滾動軸承非線性彈性支承效應、滾動軸承與阻尼環間影響、阻尼環與支座之間的耦合效應；最后采用數值積分方法求解系統微分方程組，對耦合系統振動響應進行動力學分析，獲得如下結論：

（1）對于滾動軸承支承的轉子耦合系統，在水平或垂直方向上的基礎激勵不僅對該方向轉子的振動有影響，對其他方向上的振動也有影響。

（2）當基礎振動頻率等于滾動軸承VC 頻率或其諧波頻率時，不影響系統的運動狀態；當基礎振動頻率不等于滾動軸承VC 頻率或其諧波頻率時，會呈現出組合共振現象，振動響應的頻率包括多個成分，為整數倍的滾動軸承激勵頻率與基礎激勵頻率的代數和。

（3）以轉子振動位移最小為目標，對支承阻尼環的剛度系數和損耗因子進行優化設計，可減小基礎激勵對系統動力學特性的影響。