含彈性基礎壓電功能梯度圓柱殼的振動分析

呂志鵬，劉文光，劉 超，張宇航

（南昌航空大學航空制造工程學院，南昌 330063）

在航空航天和機械工程領域，振動及振動噪聲問題普遍存在[1-3]。這些問題如不加以重視，輕則影響人的健康，重則影響設備的可靠運行。壓電智能材料由于其優異的力電轉換特性以及對環境具備可感知、可響應和可控制等特點，為結構減振降噪開辟了新途徑[4]。結合功能梯度材料（Functionally Graded Materials，簡稱FGMs）的優越性[5-6]，有研究者將目光集中在兩種材料的組合上，以提升壓電材料的工程應用價值。

目前，壓電功能梯度結構力學問題研究主要分為三大類。第一類主要是利用Maxwell方程或者變分原理直接推導出電學控制方程，對壓電功能梯度結構的振動問題開展研究。例如，應用1 階剪切變形理論并考慮von Kármán 幾何非線性，Arefi 等[7]討論了壓電功能梯度圓柱殼的非線性自由振動特性；采用1階剪切變形理論和微分求積法，段鵬飛[8]探究了熱環境下壓電功能梯度中厚圓板的自由振動響應；利用等幾何分析法，劉濤等[9]研究了不同機械邊界條件下壓電功能梯度板的自由振動、靜態彎曲和變形控制等問題。第二類主要是利用壓電材料的逆壓電效應，通過對壓電層施加電壓，探討結構的靜力變形、動力響應和控制問題。例如，應用多尺度法，劉志強[10]系統研究了簡諧力和電壓激勵下壓電功能梯度板的非線性動力響應；采用半解析法和考慮幾何非線性的Donnell殼理論，Ninh等[11]探究了含彈性基礎壓電功能梯度碳納米材料增強圓柱殼在熱-力-電荷載作用下的非線性動力響應。第三類主要是利用壓電材料的正逆壓電效應，令壓電材料分別作為壓電功能梯度結構的傳感層和作動層，開展結構主動控制問題相關研究。例如，基于高階剪切變形理論和假設模態法，Song 等[12]研究了壓電功能梯度碳納米材料增強板的主動振動控制；應用等幾何分析法和Newmark-β積分，劉濤等[13]研究了壓電功能梯度層合板的動力學響應與主動控制。利用恒速反饋控制算法和Donnell 殼理論，Dong 等[14]探究了熱環境下壓電功能梯度石墨烯增強復合圓柱殼的主動控制。

工程實際中，壓電結構與其周圍彈性介質存在相互作用，陸續有研究者探討了含彈性基礎壓電功能梯度結構的振動特性[15-16]。但是鮮有研究討論多物理場下含彈性基礎壓電功能梯度圓柱殼的動力學問題，以及壓電材料類型對壓電功能梯度圓柱殼振動特性的影響。因此，本工作以含雙參數彈性基礎壓電功能梯度圓柱殼為對象，基于一階剪切變形理論和Hamilton 變分原理，推導多場耦合載荷下壓電功能梯度圓柱殼的振動方程，討論彈性基礎、壓電材料類型等對模態頻率的影響。

1 壓電功能梯度圓柱殼模型

如圖1所示，Pasternak-Winkler彈性基礎壓電功能梯度圓柱殼的長度為L，中面半徑為R。FGM 層厚度為hf，其表面貼有壓電陶瓷，內外壓電層厚度分別為hp-I和hp-II。將圓柱殼外層壓電陶瓷沿z軸正方向極化，內層壓電陶瓷沿z軸負方向極化。在壓電功能梯度圓柱殼的中面建立圓柱坐標系（x，θ，z），其中，u0、v0和w0分別表示圓柱殼在軸向、環向及徑向的中面位移。考慮壓電功能梯度圓柱殼在軸向和徑向分別受均勻分布的靜態荷載Ax和P的作用。外表面分布Pasternak-Winkler 型彈性基礎，其中，Kp為Pasternak 型彈性基礎模量，K w為Winkler 型彈性基礎模量。

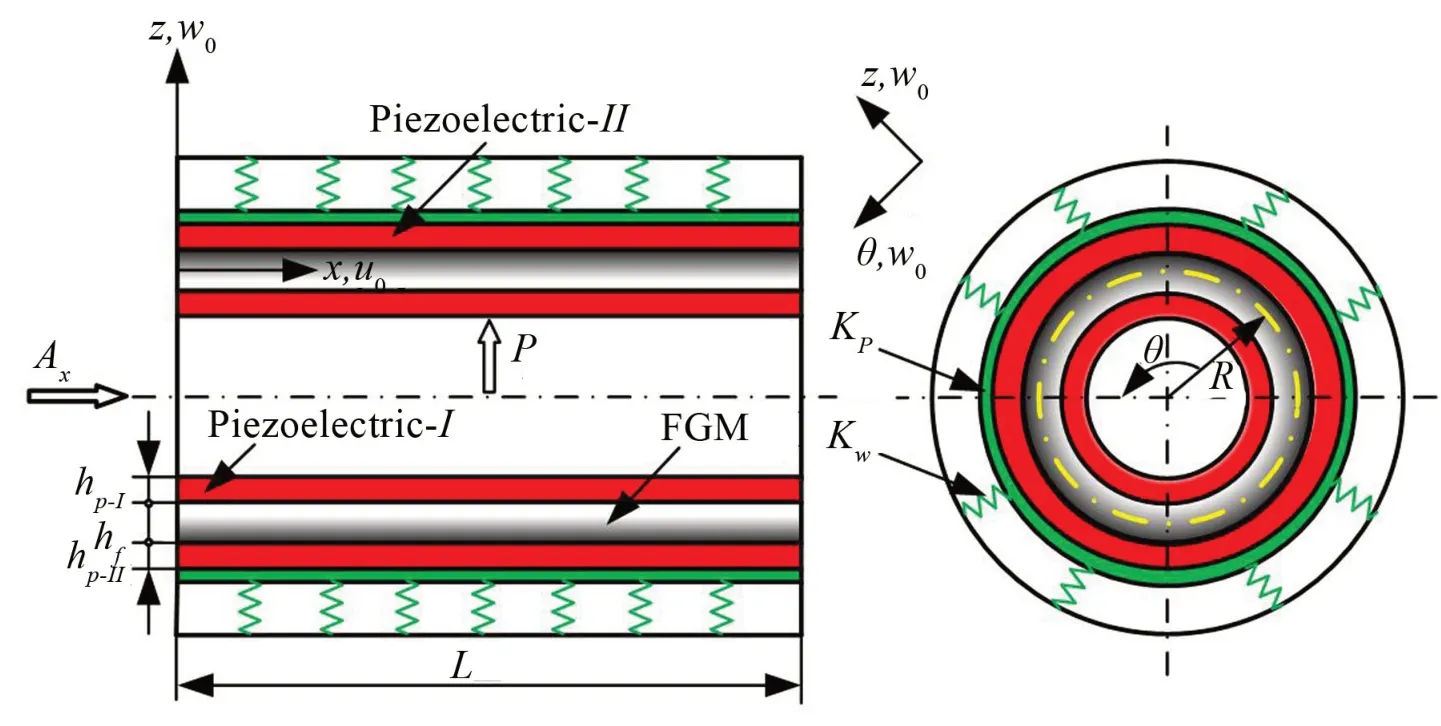
圖1 含彈性基礎壓電功能梯度圓柱殼模型

假設FGM 層的材料組分由內表面陶瓷ZrO2逐漸向外表面金屬Ti-6Al-4V 連續梯度變化，FGM 層的有效材料參數可表示為：

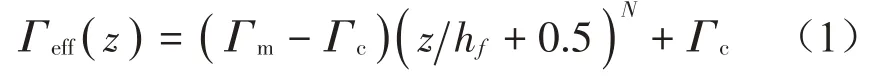
式中：Γc和Γm分別表示內外表面的材料參數；N為FGM層的陶瓷體積分數指數。

考慮溫度場沿殼體厚度方向呈線性分布，溫度場T（z）的表達式為：

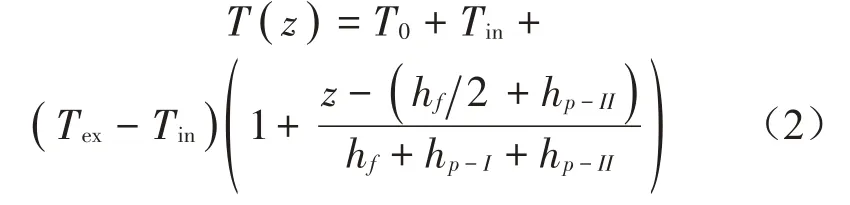
式中：環境溫度T0=300 K；Tin和Tex分別為圓柱殼內外表面的溫度。

2 壓電功能梯度圓柱殼運動方程

根據一階剪切變形理論，圓柱殼的位移分量為：

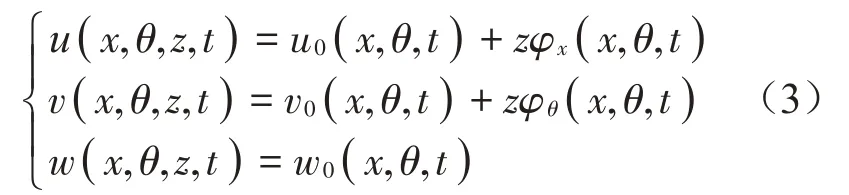
式中：u、v和w分別表示圓柱殼內任意一點的位移分量；φx和φθ為中面法線分別繞x軸和θ軸的轉角。

FGM層的應力-應變關系為：

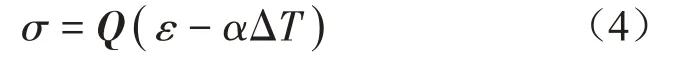
式中：ΔT=T（z）-T0；Q為縮減剛度矩陣；σ、ε和α分別為FGM層的應力、應變和熱膨脹常數向量。各矩陣和向量的表達式為：

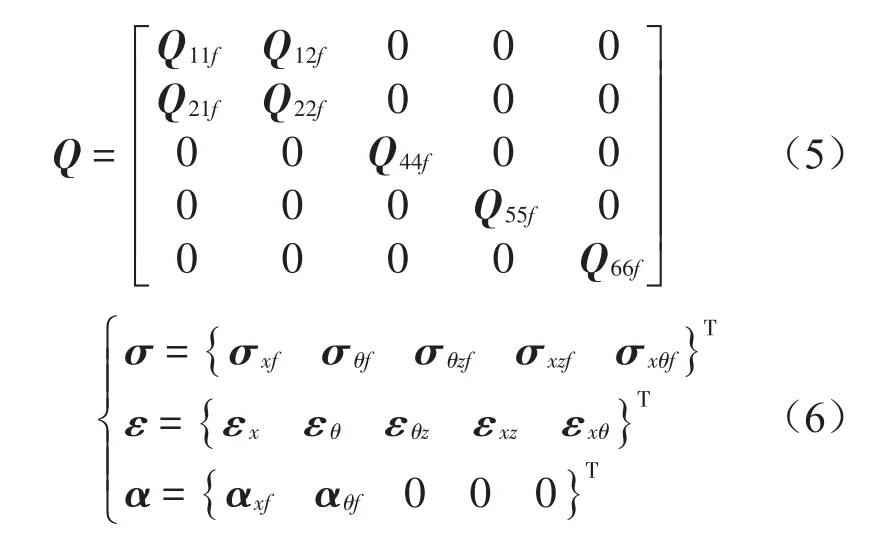
式中：縮減剛度元素Qijf（i，j=1，2，4，5，6）的表達式為：

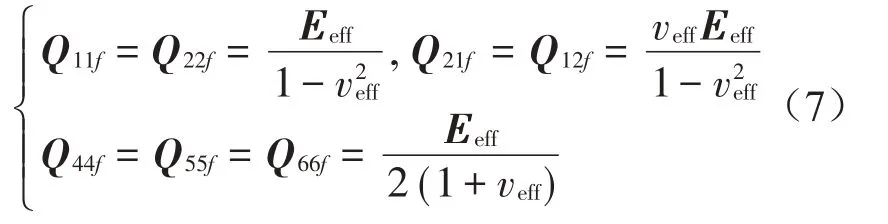
式中：Eeff和veff分別為FGM 層的有效彈性模量和泊松比。

熱、力、電耦合情形下壓電層的本構關系為：

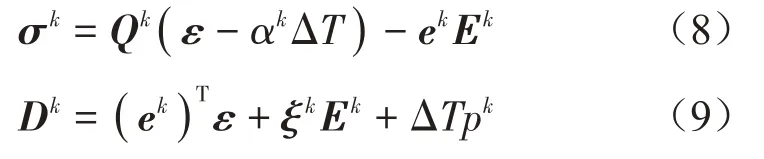
式中：上角標k=I、II分別表示內外壓電層；σk、αk、Ek、Dk和pk分別為壓電層的應力、等效熱膨脹常數、電場、電位移和等效熱釋電常數向量；Qk、ek、ξk分別為等效彈性常數、等效壓電常數和等效介電常數矩陣。這些等效常數可根據平面應力假設得出，具體表達式為：

電場強度與電勢之間的關系為：

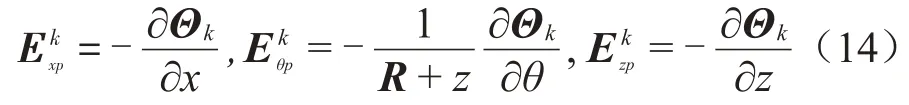
式中：Θk為在外加控制電勢V（t）作用下壓電層內的電勢分布函數，定義為：

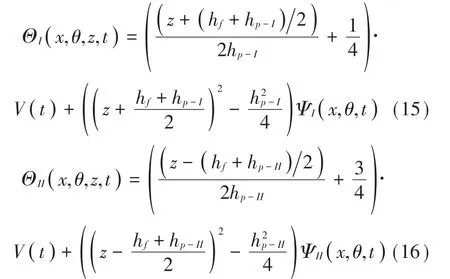
式中：Ψk（x，θ，t）是壓電陶瓷因正壓電效應產生的誘導電勢在面內的分布函數。

壓電功能梯度圓柱殼的動能K為：

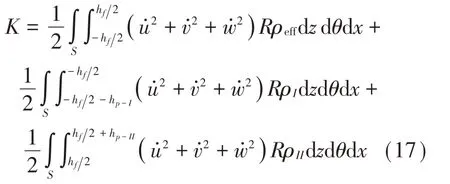
式中：ρeff和ρk分別為FGM層和壓電層的材料密度。

壓電功能梯度圓柱殼的應變能U為：

式中：

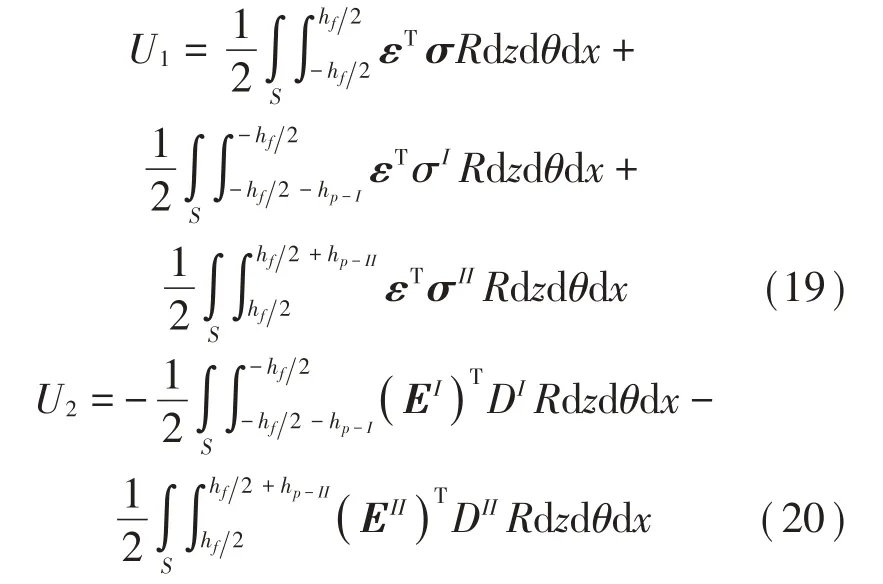
熱、力、電荷載所做總功包括[17-18]：

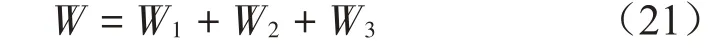
式中：

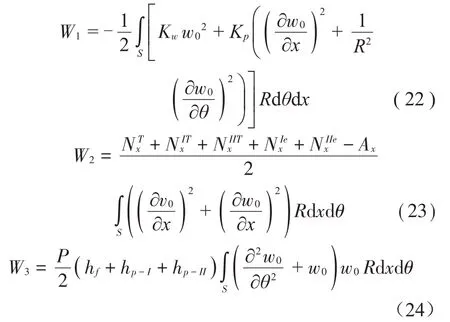
式中：NTx和NITx分別為溫度在FGM 層和壓電層的x方向引起的熱載荷；Nkex為電壓在壓電層的x方向引起的電載荷。

根據Hamilton變分原理：

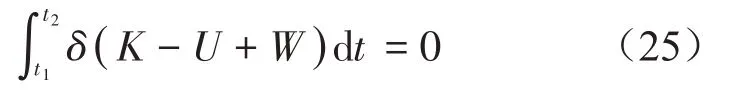
可得壓電功能梯度圓柱殼的運動方程：

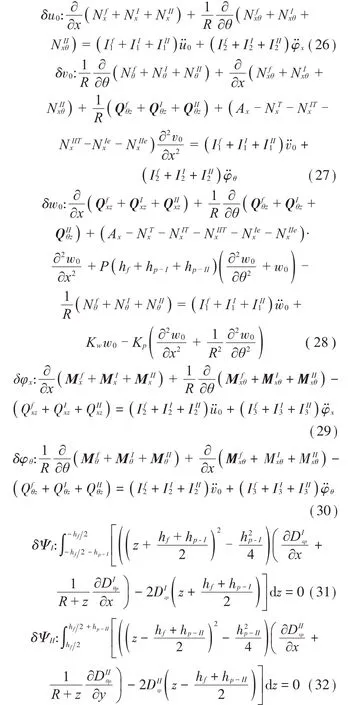
式中：Nfij和Nkij（i，j=x，θ，z）分別為FGM 層和壓電層的中面內力；Mfij和Mkij為相應各向力矩；Qfij和Qkij分別為FGM 層和壓電層在z方向的剪力；If1、If2和If3為FGM層的廣義慣性常數，Ik1、Ik2和Ik3為壓電層的廣義慣性常數。

3 模態頻率方程求解

假設壓電功能梯度圓柱殼兩端簡支，殼的中面位移和電勢函數可表示為：

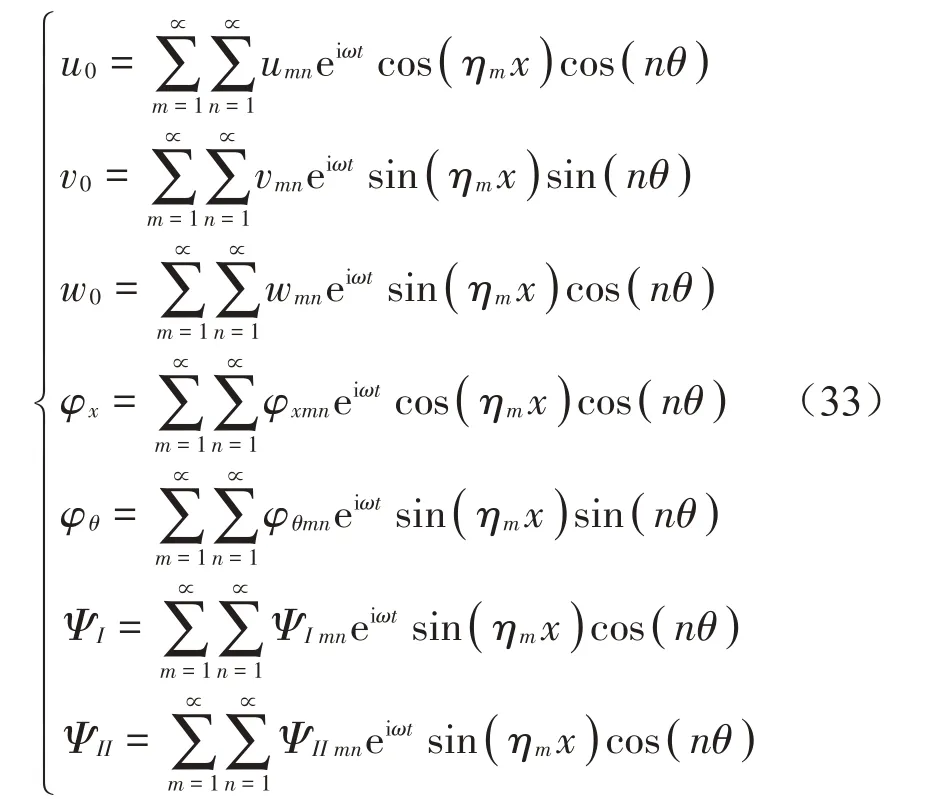
式中：ηm=mπ/L；m和n分別為軸向和環向波數；ω為壓電功能梯度圓柱殼的角頻率。

綜合上述公式得到壓電功能梯度圓柱殼在多場作用下的模態頻率方程：

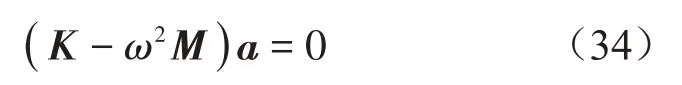
式中：M、K分別為廣義質量和廣義剛度，a為振型系數向量。求解模態方程式（34），可得壓電功能梯度圓柱殼的模態頻率。

為便于分析，定義以下無量綱參數：

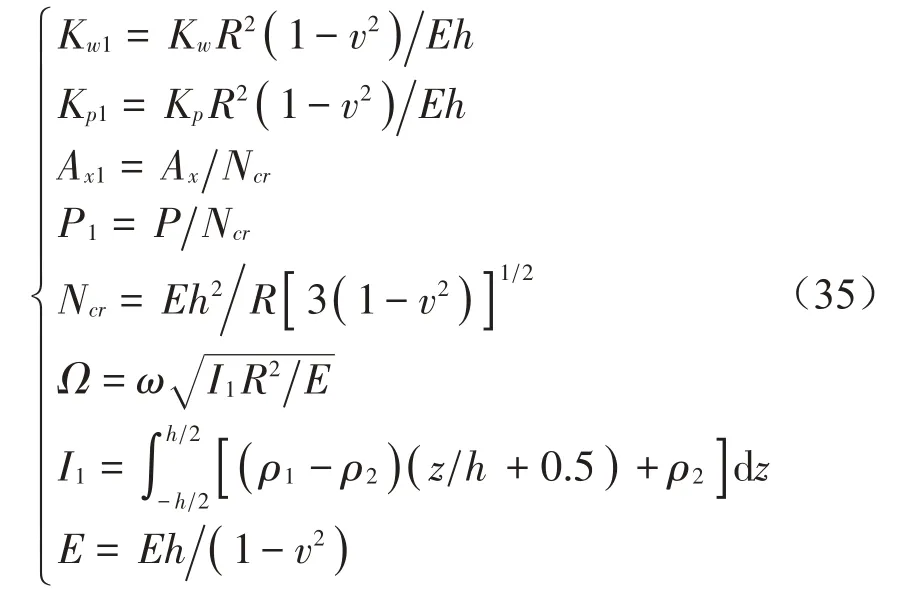
數值計算時，材料參數分別取E=70 GPa，v=0.3，ρ1=2 707 kg/m3，ρ2=30 00 kg/m3，h=0.01 m。為了驗證理論推導的合理性，將模型簡化為與文獻[19]一致的具有單層壓電層的壓電功能梯度圓柱殼。圖2為壓電功能梯度圓柱殼模態頻率隨環向波數的變化趨勢。

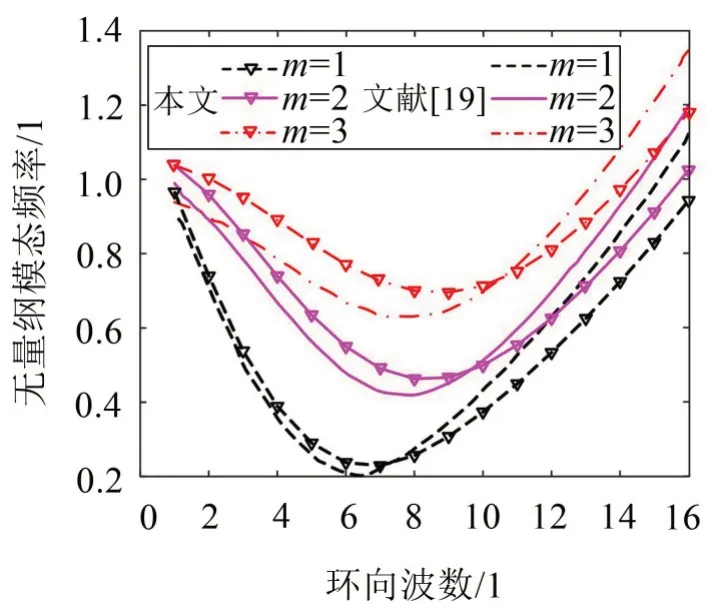
圖2 壓電功能梯度圓柱殼模態頻率隨波數的變化

表1為壓電功能梯度圓柱殼模態頻率與軸向載荷的關系。結果表明，本文模型計算的模態頻率與文獻[19]結果比較吻合。

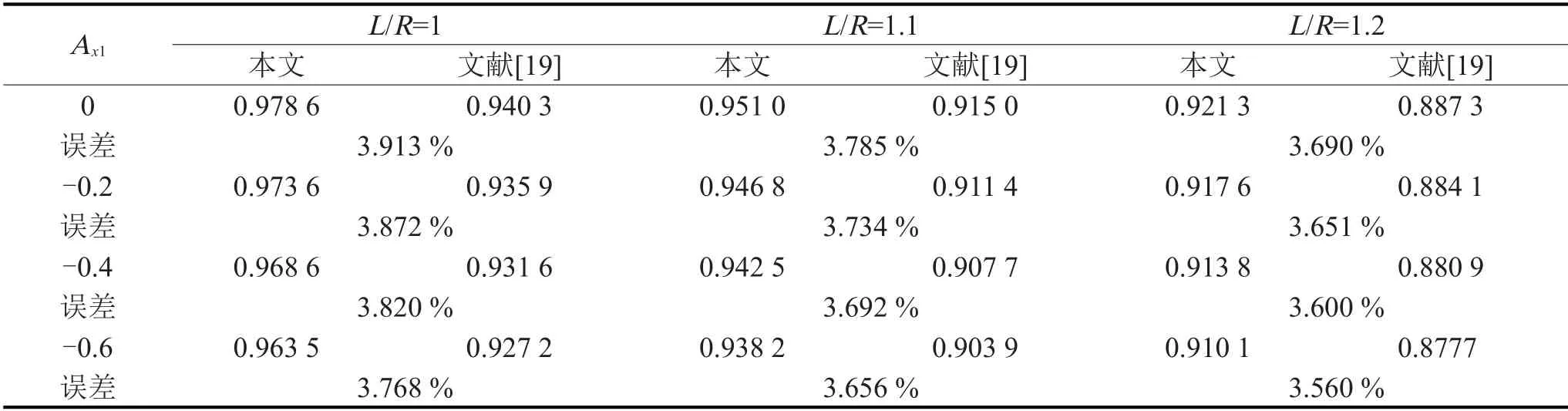
表1 壓電功能梯度圓柱殼模態頻率與軸向載荷的關系

4 分析與討論

如無特殊說明，壓電層選用PZT-4。表2為各種壓電陶瓷材料參數。功能梯度材料參數分別取：Ec=168 GPa、Em=105.7 GPa、ρc=3 000 kg/m3、ρm=4 429 kg/m3和υc=υm=0.298；圓柱殼的幾何尺寸取：L=10 m、R=1 m 和hp-I=hp-II=hf=0.001 m；軸向和環向波數取：m=3 和n=3；其他參數取：N=1，P1=100，Kw1=Kp1=0.000 1，V=100 V，Ax1=-0.5，Tin=300 K。

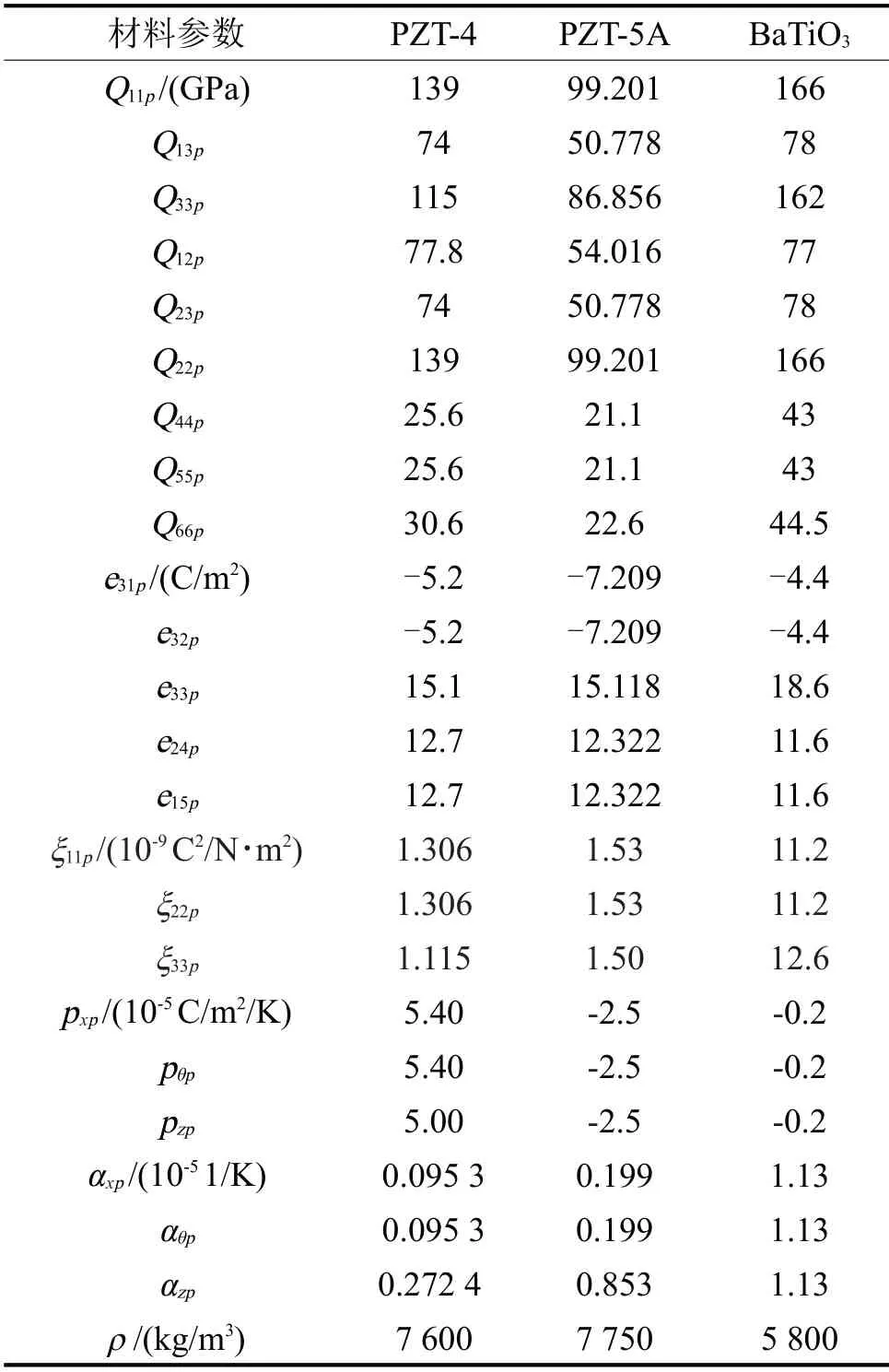
表2 各類壓電陶瓷的材料參數[20-22]

如圖3所示，研究了不同溫度梯度下，無量綱模態頻率隨彈性基礎參數的變化。結果表明：當參數Kw1或Kp1一定，增大Tin會減小圓柱殼的模態頻率。這是因為溫度降低了圓柱殼的剛度。當Tin一定時，模態頻率隨著彈性基礎參數Kw1的增大基本呈線性遞增趨勢，隨著Kp1的增大呈近似二次函數的形式，而且增長率逐漸減小。說明彈性基礎會提高圓柱殼的剛度。對比圖3（a）和圖3（b），可知彈性基礎參數Kp1比Kw1提高模態頻率顯著。

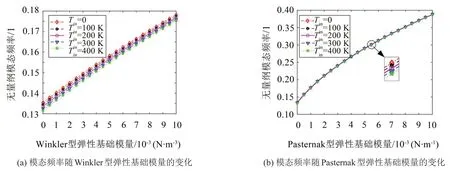
圖3 不同溫度梯度下模態頻率隨彈性參數的變化

如圖4 所示，研究了不同壓電材料時模態頻率隨彈性參數的變化。結果表明：選用不同材料時，模態頻率隨彈性參數Kw1或Kp1的變化趨勢基本相似。選用PZT-4 和PZT-5A 時模態頻率相差不大，選用BaTiO3較其他兩種材料較大程度提高模態頻率。

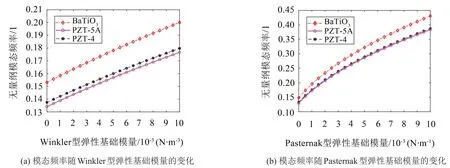
圖4 不同壓電材料下模態頻率隨彈性參數的變化

如圖5 所示，研究了不同陶瓷體積分數指數N下溫度梯度對模態頻率的影響。分析表明：Tin一定時，增大FGM 層的陶瓷體積分數指數，結構剛度因陶瓷含量增多而逐漸增大，導致模態頻率越來越大。當N增大至5 到10 時，由于材料組分逐漸趨于純陶瓷，導致模態頻率增長率逐漸減小。進一步發現，模態頻率下降率隨N的增大而逐漸增大。原因在于未考慮FGM 層的材料參數與溫度之間的依賴性。否則由于N越大，內部陶瓷含量越多，耐熱性越強，結構剛度受Tin的影響也越小。結論表明，當壓電功能梯度圓柱殼在較低溫度且忽略溫度對材料特性的影響時，選用較大的N有利于提高結構剛度，但模態頻率下降率卻越來越大；結構在較高溫度下，不能忽略溫度梯度對FGM層的材料特性影響，否則會產生較大誤差。

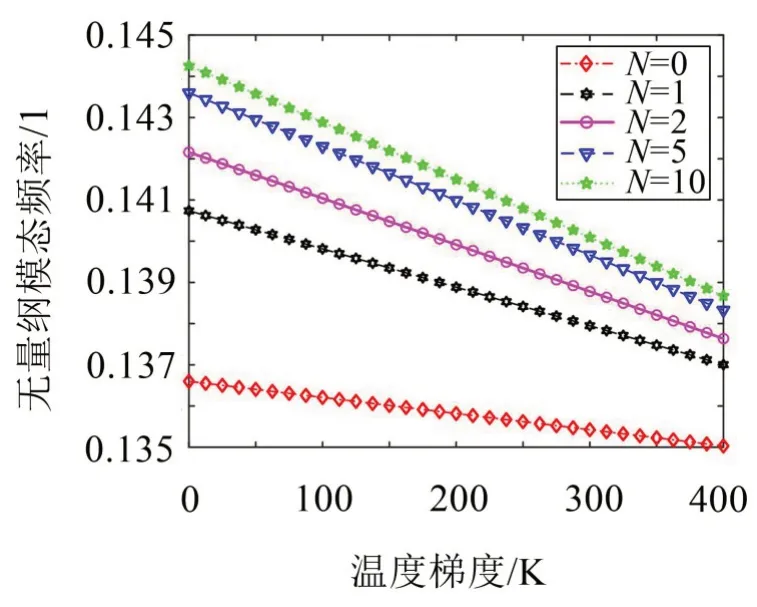
圖5 不同陶瓷體積分數下模態頻率隨溫度梯度的變化

如圖6所示，研究了不同壓電材料下，溫度梯度和陶瓷體積分數指數對模態頻率的影響。從圖6（a）可以得到，Tin一定時，盡管BaTiO3的模態頻率最大，但是其剛度受Tin的影響卻最大，而PZT-4和PZT-5A對Tin的敏感性基本一致。壓電材料對Tin的敏感性由強到弱的順序依次是BaTiO3＞PZT-4=PZT-5A。從圖6（b）可以得到，不同壓電材料下，改變FGM 層的N，結構模態頻率變化趨勢基本一致。且均在N≤2時，模態頻率隨著N的增大先快速增大，然后逐漸趨于平穩。結論表明，壓電材料的種類不影響模態頻率隨N的變化趨勢；為使FGM層含有一定的剛度和強度，N控制在2左右較好。

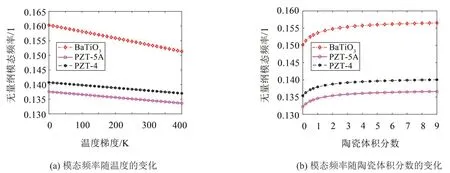
圖6 不同材料下模態頻率隨溫度和陶瓷體積分數的變化

如圖7 所示，研究了不同溫度梯度和壓電材料下模態頻率隨激勵電壓V的變化。結果顯示，不同Tin下，激勵電壓對模態頻率的影響趨勢基本一致，且隨著激勵電壓的增大，模態頻率出現微小降幅。進一步分析得到，溫度梯度相對外激勵電壓對結構剛度的影響更為顯著。圖7（b）中Ω/ΩV=0表示結構模態頻率與激勵電壓V=0 時模態頻率的比值。可以看到，激勵電壓對選用PZT-5A 時模態頻率的影響最大，而選用BaTiO3時的影響最小。

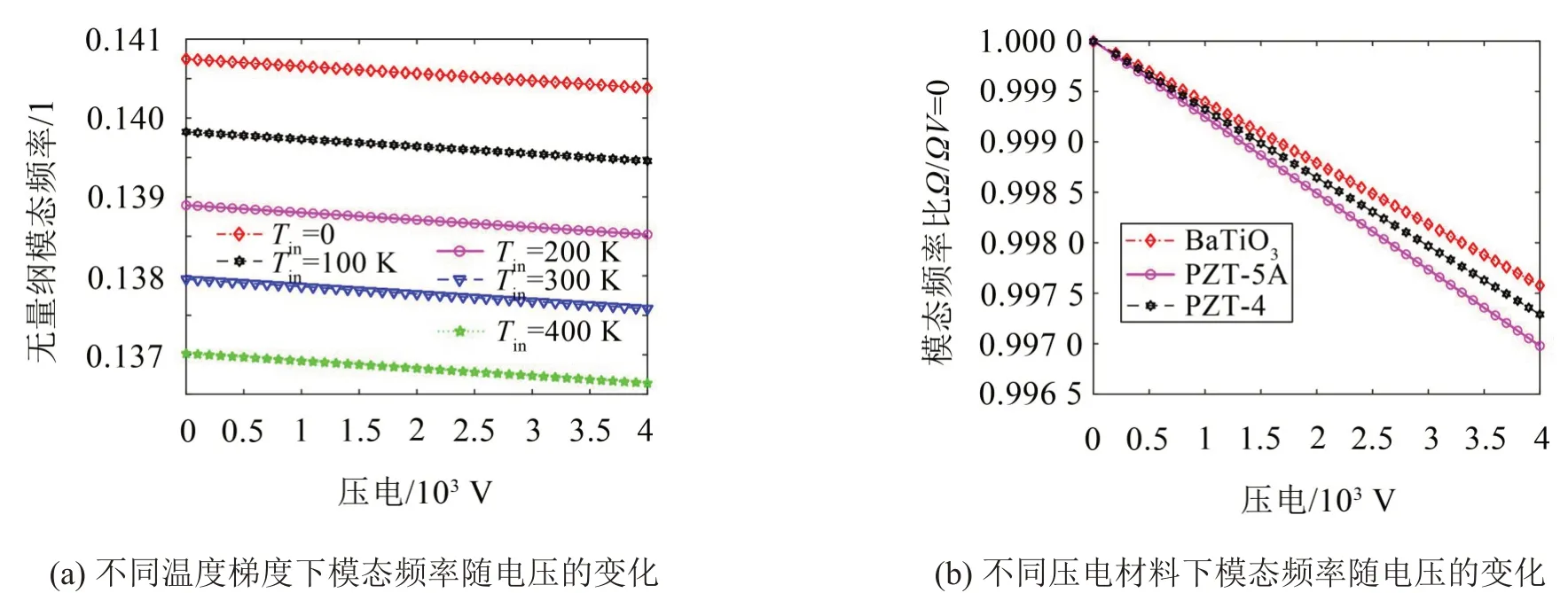
圖7 不同溫度梯度和壓電材料下模態頻率隨電壓的變化

5 結語

基于1階剪切變形理論和Hamilton變分原理推導了多場載荷下含彈性基礎壓電功能梯度圓柱殼的振動方程，分析了不同參數對模態頻率的影響。主要結論如下：

（1）增大溫度梯度會降低壓電功能梯度圓柱殼的模態頻率，且高溫下不宜忽略FGMs 屬性的溫度依賴性；增大彈性參數Kw和Kp會增大層合圓柱殼的模態頻率，但Kp提高模態頻率顯著；隨著FGM 層陶瓷體積分數的增大，模態頻率也越來越大。

（2）壓電功能梯度圓柱殼模態頻率值與壓電材料的關系為BaTiO3＞PZT-4＞PZT-5A；BaTiO3對溫度梯度的敏感性最強，其他壓電材料基本相同。

（3）選用PZT-5A 圓柱殼的模態頻率受外激勵電壓的影響最大，而選用BaTiO3則相反；與溫度梯度相比，外激勵電壓對結構剛度的影響較小。

（4）受條件限制，本文未針對研究對象開展實驗測試以驗證理論推導的合理性。為了加速推進FGMs 在工程實踐中的應用，下一步將重點開展壓電功能梯度圓柱殼的振動實驗研究。