基于貪婪策略的緊密k 核子圖查詢

趙丹楓，姚賢標(biāo)，包曉光，黃冬梅，郭偉其

（1.上海海洋大學(xué) 信息學(xué)院，上海 201306；2.上海電力大學(xué) 電子與信息工程學(xué)院，上海 200090；3.國家海洋局 東海海洋環(huán)境調(diào)查勘察中心，上海 200137）

0 概述

圖查詢是圖數(shù)據(jù)分析與處理的基礎(chǔ)，其中社團檢測作為一種子圖查詢，其目標(biāo)是從給定的圖中尋找所有緊密連接的子圖，并且各個圖內(nèi)部的節(jié)點是連通的［1］。緊密子圖查詢作為社團檢測的核心，在很多領(lǐng)域都有著重要的應(yīng)用，例如：在社交網(wǎng)絡(luò)中，查詢聯(lián)系緊密的社團有助于用戶的特征分析［2］；在作者的合作網(wǎng)絡(luò)中，聯(lián)系緊密的作者之間可能具有相似的研究領(lǐng)域［3］；在商品銷售數(shù)據(jù)中，聯(lián)系緊密的商品更有可能被相似的消費者所關(guān)注［4］；在蛋白質(zhì)網(wǎng)絡(luò)中，關(guān)系緊密的蛋白質(zhì)通常更有可能形成特定的官能團［5］。

在現(xiàn)有的研究中，研究人員提出許多社團檢測方法，如基于模塊度優(yōu)化的算法［6］、譜方法［7］、非負(fù)矩陣分解［8］等。對于社團的定義也有多種，常見的有k架（k-truss）、k團（k-clique）、k核（k-core）等，其中k核的定義［9］要求圖中每個節(jié)點至少有k個鄰接節(jié)點，即每個節(jié)點的度至少為k。k核可以在線性時間復(fù)雜度內(nèi)計算得到，具有較好的應(yīng)用基礎(chǔ)［10-12］。近年來的研究多結(jié)合部分場景的應(yīng)用需求，討論各類屬性圖上的k核子圖查詢［13-15］。然而，由于考慮邊權(quán)值的研究較少，但在很多場景下，圖中邊的權(quán)值往往具有很強的語義關(guān)系。例如在社交網(wǎng)絡(luò)中，兩個用戶之間的交流越頻繁意味兩者之間的聯(lián)系越緊密。在作者的合作網(wǎng)絡(luò)中，若兩個作者之間合作的次數(shù)越多，則說明他們的聯(lián)系越緊密，對應(yīng)圖中邊的權(quán)值越大。因此，為了使社團檢測更加符合實際的語義場景，提高查詢結(jié)果的合理性，則需要將圖中邊的權(quán)值考慮在內(nèi)。

此外，考慮到查詢最緊密社團往往會耗費較多的時間，并且在一些應(yīng)用場景下不需要查詢社團權(quán)重的最值，例如在蛋白質(zhì)網(wǎng)絡(luò)中，有時僅需要找到滿足一定緊密關(guān)系的蛋白質(zhì)集合即可。為此，不局限于社團檢測中最值的查詢，給定核值k、節(jié)點平均權(quán)值wQ，在加權(quán)圖中查詢聯(lián)系緊密的連通k核子圖問題，記為緊密k核子圖查詢（Closely Relatedk-Core Subgraph Query，CRKSQ）問題。該問題要求查詢得到的連通k核子圖的節(jié)點平均權(quán)值大于等于wQ，其進一步限制了子圖的緊密程度，且由于wQ可以根據(jù)實際需求給出，具有更好的靈活性，更加切合實際應(yīng)用場景。

為解決CRKSQ 問題，本文首先證明該問題是一個NP-難問題，即無法為其找到一個在多項式時間復(fù)雜度內(nèi)的最優(yōu)算法，并基于貪婪策略設(shè)計啟發(fā)式算法CRK-G。在此基礎(chǔ)上，研究CRK-G 算法的優(yōu)化策略，提出CRK-C 和CRK-F 算法，分別從降低圖規(guī)模和減少迭代次數(shù)兩個方面提高查詢效率。最后通過實驗對比3 種算法在不同場景下的效率。

1 相關(guān)工作

目前針對社團的查詢已經(jīng)有了廣泛的研究，除k核外，主要還包括基于k-truss和k-clique 的查詢問題。k-truss和k-clique 相對于k核有著更加嚴(yán)格的定義，但都與k核類似，其本身并未考慮圖中的其他屬性，僅僅只是從圖中尋找稠密且內(nèi)聚的結(jié)構(gòu)。近年來的很多研究也開始結(jié)合圖的語義關(guān)系，探索更加高質(zhì)量的k-truss和k-clique 社團［16-18］。

與上述兩種社團的定義相比，k核可以被有效地在線性時間內(nèi)計算，其概念最初由SEIDMAN［9］在1983 年提出。為了高效地進行k核的查詢，BATAGELJ等［19］于2003 年提出了k核分解算法，其能在O(m)時間復(fù)雜度下得到每個節(jié)點的最大核值，進而能夠在線性時間內(nèi)得到k核查詢的結(jié)果。文獻［20］為應(yīng)對大圖的查詢，又提出了效率更高且能在個人計算機上運行的3種k核分解算法，其查詢速度有了很大的提升。為提升k核查詢的效率，文獻［21］提出了面向k核查詢的圖壓縮算法SC，進一步將壓縮圖轉(zhuǎn)化為樹的算法TC，其算法效率比可以比直接在原圖上查詢的效率高出1～2 個數(shù)量級。

為了優(yōu)化k核社團查詢，文獻［22］提出一種能夠支持多個節(jié)點查詢的社團搜索問題，解決了以往單節(jié)點查詢帶來的通用性的不足。文獻［23］考慮到現(xiàn)有的社團查詢方法使用的都是全局搜索，算法代價較高，故提出一種局部搜索方法。上述兩種方法雖然在查詢條件上做了優(yōu)化，但卻都未結(jié)合圖上的其他屬性，僅面向簡單圖的查詢。

近年來，研究人員開始致力于尋找更加緊密的k核子圖，文獻［13］結(jié)合圖中節(jié)點的影響力，提出了k-influential 社團模型，用于在大圖中查詢最具影響的社團。文獻［14］考慮邊的有向性，研究了有向圖上的社團搜索問題，其利用最小內(nèi)度和外度的度量方法尋找緊密連接的子圖。文獻［15］研究了輪廓圖的社團搜索（PCS）問題，其能夠識別具有語義共性的節(jié)點，從而發(fā)現(xiàn)更多高質(zhì)量的社團。上述研究結(jié)合了圖上的其他屬性，在相應(yīng)的場景下能得到更加合理有效的社團，而對于邊權(quán)值屬性的社團查詢方面，目前的研究還不充分。雖然文獻［24］提出了查詢加權(quán)圖的親密核心組問題，但由于其模型屬于社團搜索，僅針對給定節(jié)點集的查詢，并且是查詢總權(quán)值最小的子圖，與部分應(yīng)用場景不符，具有一定的局限性。

本文考慮了節(jié)點的語義關(guān)系，不局限于社團檢測中最值的查詢，提出了在加權(quán)圖中查詢聯(lián)系緊密的連通k核子圖問題，以實現(xiàn)更好的靈活性，且更貼合實際應(yīng)用場景。

2 定義與證明

2.1 緊密k 核子圖的定義

本文研究的是無向加權(quán)圖上的子圖查詢，該研究是在k核的基礎(chǔ)上進行的，故先給出k核的定義。

定義1（k核）［9］給定圖G=(V，E)，k核是圖G的極大子圖H，使得H中的每個節(jié)點至少有k個鄰節(jié)點。

定義2（核值）給定圖G=(V，E)，對于G中的節(jié)點u，u∈V，u的核值core(u)為u所在全部k核中的最大值，即：

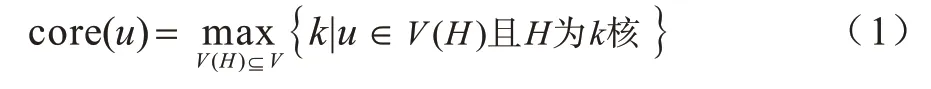
例如，在圖1 中，節(jié)點集｛a，b，c，d，f｝和｛o，p，r，s｝的導(dǎo)出子圖中節(jié)點核值都為3。但需要注意的是，節(jié)點的核值并不等于節(jié)點的度，如圖1 中的節(jié)點c，其節(jié)點的度為4，但核值卻為3。此外，k核并不一定是一個連通的圖，如圖1（b）表示的是圖1（a）中加權(quán)圖G的3 核子圖，該圖并不是連通的。

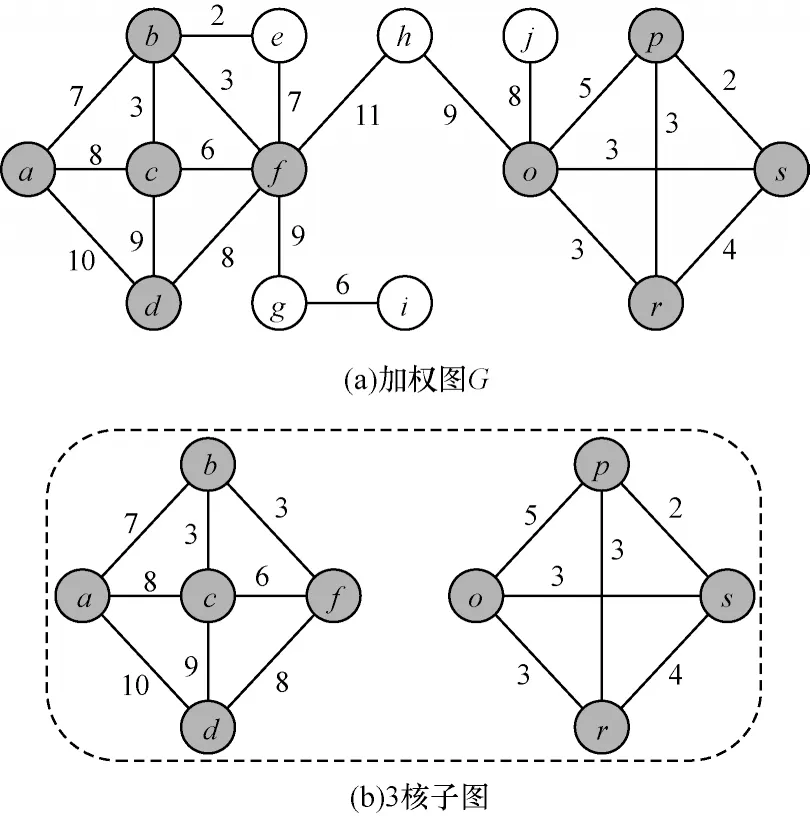
圖1 k 核查詢實例Fig.1 Example of k-core query

定義3（連通k核）給定圖G=(V，E)，連通k核是圖G的極大連通子圖H，使得H中的每個節(jié)點至少有k個鄰節(jié)點。

連通k核是在k核的基礎(chǔ)上定義的，其表示的子圖一定是一個連通的圖。本文研究的是連通k核，若不加特別說明，下文中提到的k核均表示的是連通k核。

定義4（節(jié)點權(quán)值ω）給定一個加權(quán)圖G=(V，E，W)，對于G中的節(jié)點u，u∈V，節(jié)點u的權(quán)值為與其相連邊的權(quán)值之和，即節(jié)點權(quán)值：

例如，在圖1 中，與節(jié)點a相連的邊有3 條，各邊權(quán)值分別為7、8、10，故其節(jié)點的權(quán)值ω（a）=7+8+10=25。

定義5（節(jié)點平均權(quán)值A(chǔ)w）給定一個加權(quán)圖G=(V，E，W)，圖G節(jié)點平均權(quán)值為每個節(jié)點的權(quán)值之和除以圖G的節(jié)點數(shù)，即圖G節(jié)點平均權(quán)值為：

節(jié)點平均權(quán)值反映的是整個子圖內(nèi)部的緊密程度，節(jié)點平均權(quán)值越大則說明子圖內(nèi)部節(jié)點之間的交互越多，子圖就越緊密。

下面給出緊密k核子圖（Closely Relatedk-Core Subgraph）的定義。

定義6（緊密k核子圖）給定一個加權(quán)圖G=(V，E，W)，核值k，節(jié)點平均權(quán)值wQ，緊密k核子圖H=(V'，E'，W)，H滿足以下條件：1）H?G；2）H是連通k核；3）圖H的節(jié)點平均權(quán)值A(chǔ)w(H)≥wQ。

緊密k核子圖的定義在k核的基礎(chǔ)上進一步限制了子圖的節(jié)點平均權(quán)值，該限制將會消除圖中權(quán)值較小的節(jié)點，使得圖整體的緊密性有所提高。

緊密連接k核子圖查詢?nèi)鐖D2 所示，其中圖2（b）為加權(quán)圖G（見圖1（a））在給定k=2、wQ=20 時得到的緊密2 核子圖H。圖H的每個節(jié)點都至少有2 個鄰節(jié)點，且圖的節(jié)點平均權(quán)值為21.6，滿足給定條件。對比圖2（a）和圖2（b），可以看出后者節(jié)點之間的聯(lián)系更加緊密，整體也更加緊湊。

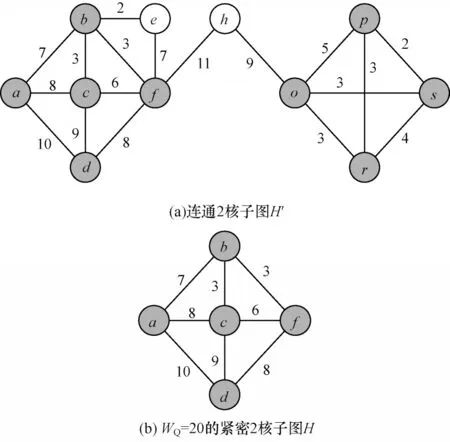
圖2 緊密連通k 核子圖的查詢實例Fig.2 Example of closely related connected k-core subgraph query

定義7（緊密k核子圖查詢）給定一個加權(quán)圖G=(V，E，W)，核值k，節(jié)點平均權(quán)值wQ，在圖G中尋找緊密k核子圖H。

緊密k核子圖查詢（CRKSQ）問題的目的是在圖中找到滿足條件的緊密k核子圖。需要注意的是，緊密k核子圖在圖中不一定只有一個，有可能存在多個。

2.2 QCRKS 問題的證明

引理1給定一個加權(quán)圖G=(V，E，W)，圖G中節(jié)點權(quán)值之和等于圖G中各邊權(quán)值之和的兩倍，即：

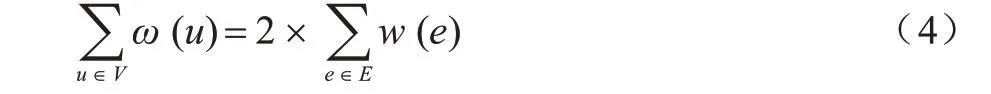
證明由于圖G中的每條邊連接兩個節(jié)點，而根據(jù)節(jié)點權(quán)值的定義可知圖中每條邊的權(quán)值會被相連的兩個節(jié)點各計算一次，故上述結(jié)論成立。

定理1CRKSQ 問題是NP-難的。

證明將clique 問題多項式歸約到CRKSQ 問題。由于clique 問題是一個NP-完全問題［25］，進而得出CRKSQ 問題是NP-難的。給定clique 問題的一個實例I，其由一個無權(quán)圖G=(V，E)和一個正整數(shù)k構(gòu)成。構(gòu)造CRKSQ 問題的一個實例I'：一個加權(quán)圖G'=(V，E，W)，這里每條邊權(quán)值都為1；另一個正數(shù)wQ=k-1。顯然，這是一個多項式歸約。下面只需證明實例I存在一個k階完全子圖，當(dāng)且僅當(dāng)，實例I'存在一個節(jié)點平均權(quán)值大于等于wQ(wQ=k-1)的緊密(k-1)核子圖。

假設(shè)clique 問題存在一個k階完全子圖H。現(xiàn)證明H作為G'的子圖，其是一個滿足條件的緊密(k-1)核子圖。由完全子圖的定義可知，H中的每個節(jié)點具有(k-1)個鄰接節(jié)點，且平均權(quán)值為：

根據(jù)引理1，式（5）可化為：

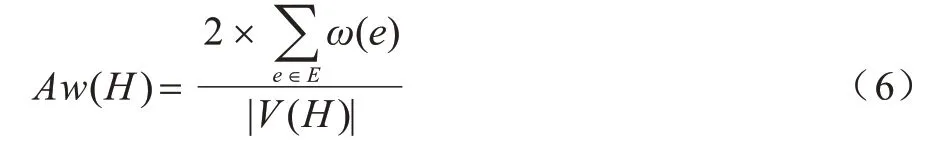
因G'中每條的權(quán)值都為1，故：

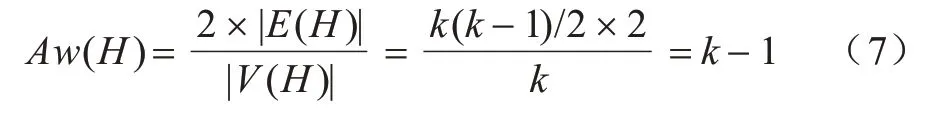
得證。

反之，假設(shè)G'中存在一個滿足條件的緊密(k-1)核子圖H。由子圖H是一個(k-1)核知，H具有至少k個節(jié)點；由節(jié)點平均權(quán)值大于等于wQ(wQ=k-1)，并由引理1 可知，H具有k(k-1)條邊，因此作為G'的子圖H是一個k階完全子圖。得證。

3 基于貪婪策略的查詢算法

由定理1 可知，無法為CRKSQ 問題找到一個多項式時間復(fù)雜度的最優(yōu)算法，為解決該問題并在可接受的時間內(nèi)找到合適的解，本文基于貪婪策略提出了啟發(fā)式算法CRK-G。首先從圖中找到候選k核子圖，然后通過不斷地迭代刪除候選子圖中權(quán)值最小的節(jié)點，進而得到滿足條件的緊密k核子圖。

3.1 CRK-G 算法

CRK-G 算法步驟如下：

步驟1使用k核分解算法［20］計算每個節(jié)點的核值。

步驟2使用廣度優(yōu)先搜索，得到候選k核子圖集合。

步驟3判斷子圖節(jié)點平均權(quán)值是否小于wQ，若小于則迭代刪除圖中權(quán)值最小的節(jié)點。

步驟4為了保證剩余子圖的k核連通性，還需要刪除圖中節(jié)點度小于k的節(jié)點，隨后判斷子圖是否連通，若不連通則將每個獨立的連通子圖分隔，并加入候選子圖集合等待后續(xù)的處理。

步驟5重復(fù)上述操作，直到剩余子圖的節(jié)點平均權(quán)值大于等于wQ，或節(jié)點被全部迭代刪除為止。算法最后返回滿足條件的緊密k核子圖集。

例如，在圖2 中，給定圖G（見圖1（a）），核值k=2，節(jié)點平均權(quán)值wQ=20。算法首先查詢得到候選2 核子圖H'，隨后開始判斷子圖H'的節(jié)點平均權(quán)值是否大于等于wQ，經(jīng)計算可知節(jié)點平均權(quán)值小于20。因此，開始刪除最小權(quán)值的節(jié)點e。刪除節(jié)點e后，節(jié)點平均權(quán)值仍然小于20，則再依次刪除節(jié)點s、節(jié)點r。其中，刪除節(jié)點s和節(jié)點r導(dǎo)致節(jié)點p的度小于2，則再將節(jié)點p刪除，此時剩余子圖仍然是連通的。重復(fù)上述步驟再依次刪除節(jié)點o、節(jié)點h，最終得到圖2（b）中滿足條件的緊密2 核子圖H。

算法1緊密k核子圖查詢算法CRK-G

3.2 CRK-G 算法的復(fù)雜度分析

CRK-G 算法采用貪婪思想，通過迭代刪除節(jié)點而使得子圖滿足條件，其主要時間花費包括k核候選子圖查詢、節(jié)點平均權(quán)值計算、子圖連通性判斷以及子圖k核的維護。首先，在k核候選子圖的查詢方面，使用的是廣度優(yōu)先搜索算法，其時間復(fù)雜度為O(|V|+|E|)。其次，在節(jié)點平均權(quán)值計算和子圖連通性判斷方面，計算節(jié)點平均權(quán)值需要耗時O(|E|)，尋找最小權(quán)值的節(jié)點需要耗時O(|V|)，若算法需要迭代t次，則計算節(jié)點平均權(quán)值耗時O(t(|V|+|E|))。連通性判斷使用的是廣度優(yōu)先搜索，耗時也為O(t(|V|+|E|))。最后，在子圖k核的維護方面，查詢節(jié)點的度耗時為O(|E|)，若算法需要迭代t次，則這一步總耗時為O(t(|E|))。最終CRK-G 算法的時間復(fù)雜度為O(t(n+m))，其中n和m分別表示原圖的節(jié)點數(shù)和邊數(shù)。

下文分析CRK-G 算法的空間復(fù)雜度，對于原圖中的每個節(jié)點，需要存儲其鄰節(jié)點以及其與鄰節(jié)點之間邊的權(quán)值，所以空間消耗為O(2|E|)。另外，還需要存儲候選子圖中節(jié)點的鄰節(jié)點以及節(jié)點與鄰節(jié)點之間邊的權(quán)值，空間消耗為O(2|E|)。總共空間消耗為O(4|E|)，故CRK-G 算法的空間復(fù)雜度為O(m)。

4 CRK-G 算法的優(yōu)化

CRK-G 算法對于CRKSQ 問題的求解是有效的，它能在O(t(n+m))時間內(nèi)找到一個解，但對于在大規(guī)模圖上的查詢而言，該算法求解需要花費大量的時間，效率較低。

根據(jù)對CRK-G 算法時間復(fù)雜度的分析，影響其效率的主要因素是圖的規(guī)模和迭代的次數(shù)，因此可以通過使用降低圖規(guī)模或減少迭代次數(shù)的方法，使得算法的效率提高。基于該思路，本節(jié)提出了CRK-G 算法的兩種改進算法：1）使用圖壓縮策略的CRK-C 算法，其適用于節(jié)點權(quán)值差異性較小的圖數(shù)據(jù)；2）使用單次多節(jié)點刪除策略的CRK-F 算法，該算法實現(xiàn)簡單，效率提高明顯，適用于差異性較大或無法確定差異性的圖數(shù)據(jù)。

4.1 基于圖壓縮的優(yōu)化策略

目前關(guān)于面向特定查詢的圖壓縮已經(jīng)有了廣泛的研究，常見的如面向保持可達查詢的圖壓縮［26］、面向鄰節(jié)點查詢的壓縮［27］以及面向k核查詢的圖壓縮［21］。與大部分面向特定查詢的壓縮技術(shù)類似，本文的壓縮方法遵循查詢等價原則，通過將權(quán)值相近的節(jié)點合并得到超節(jié)點，判斷超節(jié)點所包含的節(jié)點在原圖中是否存在邊來構(gòu)建超邊以及超邊的權(quán)值。

定義8（超節(jié)點和超邊）給定圖G=(V，E)，其經(jīng)過壓縮后得到GC=(V'，E')，其中，由原圖節(jié)點集V分割得到，即?V(i=1，2，…，n)，并且，則節(jié)點v'∈V'被稱為超節(jié)點，邊e'∈E′被稱為超邊。

例如，圖3（b）的圖H'C表示的是一個壓縮圖，其每個節(jié)點表示的即為超節(jié)點，如超節(jié)點s1包含了原圖H'中的節(jié)點a、節(jié)點c和節(jié)點d。壓縮圖中的邊即為超邊。

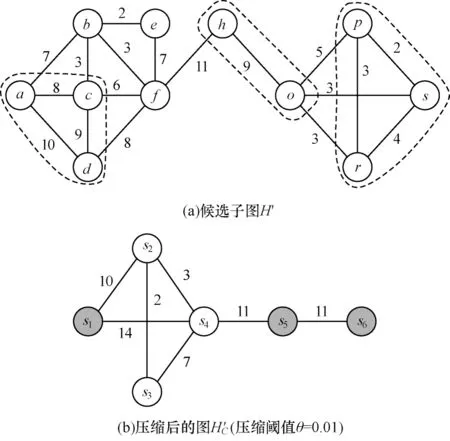
圖3 圖壓縮實例Fig.3 Example of graph compression

定義9（壓縮比cr）給定圖G=(V，E)，其經(jīng)過壓縮得到GC=(V'，E')，則壓縮比為：

壓縮比是衡量圖壓縮是否有效的重要指標(biāo)，根據(jù)壓縮比的定義可知，壓縮比越小，則壓縮后的圖規(guī)模也越小。

4.1.1 CRK-C 算法

CRK-C 算法在CRK-G 算法的基礎(chǔ)上進行，查詢到候選k核子圖集后，對每個候選子圖進行壓縮，得到壓縮后的圖GC，在后續(xù)的迭代刪除過程中直接對GC進行操作。壓縮算法步驟如下：

步驟1遍歷圖中的所有節(jié)點，將權(quán)值相近的節(jié)點合并，從而得到超節(jié)點。

步驟2超節(jié)點包含的節(jié)點若在原圖中存在邊，則在超節(jié)點之間構(gòu)建超邊。

步驟3超邊的權(quán)值設(shè)為兩個超節(jié)點所包含的原節(jié)點在原圖中邊權(quán)值之和。

其中，步驟1 的節(jié)點合并是通過設(shè)置壓縮閾值θ（θ∈（0，1）），根據(jù)起始節(jié)點的權(quán)值ω，將節(jié)點權(quán)值在±θω之間的連通節(jié)點進行合并。

例如，圖3（a）表示的是一個2核候選子圖，節(jié)點a、節(jié)點c和節(jié)點d的權(quán)值分別為ω(a)=25、ω(c)=26、ω(d)=27，節(jié)點之間的最大差值為2，當(dāng)壓縮閾值θ=0.01 時，最大允許的權(quán)值差值為2.5（θω(a)=2.5），所以節(jié)點a、節(jié)點c和節(jié)點d可以被壓縮為一個超節(jié)點s1。由于圖H'中節(jié)點a、節(jié)點c與節(jié)點b存在邊，而節(jié)點b壓縮后由超節(jié)點s2表示，因此超節(jié)點s1和超節(jié)點s2之間存在邊，邊的權(quán)值為原圖中邊（a，b）和邊（c，b）的權(quán)值之和，即7+3=10。重復(fù)上述壓縮步驟，最終該候選子圖H'經(jīng)過壓縮得到了圖H'C，壓縮后圖的規(guī)模與原圖H'對比明顯有所降低，壓縮比cr=

7/18≈0.39。

壓縮算法GC-W 見算法2，算法最后返回壓縮后的圖GC和映射表M，M中記錄了原圖G中每個節(jié)點所對應(yīng)的超節(jié)點。借助M，可以在O(n)時間內(nèi)將壓縮后的圖解壓縮，n表示的是原圖的節(jié)點數(shù)。

需要注意的是，壓縮閾值θ越大，算法查詢速度越快，但對應(yīng)著查詢結(jié)果的誤差也會增大。根據(jù)算法特點，壓縮閾值θ的取值誤差主要取決于候選子圖節(jié)點權(quán)值的波動或偏移程度，故可以使用子圖中節(jié)點權(quán)值的差異系數(shù)（Coefficient of Variation，CV）作為θ的取值依據(jù)，其反映了子圖節(jié)點權(quán)值的離散程度，計算公式為：

其中：σw為子圖權(quán)值的標(biāo)準(zhǔn)差；Aw為子圖平均節(jié)點權(quán)值。

算法2壓縮算法GC-W

4.1.2 CRK-C 算法的復(fù)雜度分析

CRK-C 算法在原有貪婪策略的基礎(chǔ)上新增了圖壓縮的步驟，其主要的時間花費包括k核候選子圖查詢、圖壓縮、節(jié)點平均權(quán)值計算、子圖連通性判斷、子圖k核維護以及最后壓縮圖的解壓縮。

1）在k核候選子圖查詢方面，其時間復(fù)雜度與CRK-G 算法一致，都為O(|V|+|E|)。

2）在圖壓縮方面，其主要由超節(jié)點劃分和創(chuàng)建超邊兩部分組成。其中超節(jié)點劃分是通過廣度優(yōu)先搜索算法，不斷地擴展與節(jié)點u權(quán)值相近的節(jié)點，直至無法擴展為止，該步可以在O(|V|+|E|)時間內(nèi)完成；而超邊的創(chuàng)建是通過依次訪問原圖G中的每一條邊，從而確定壓縮圖的邊集，則其時間復(fù)雜度為O(|E|)。因此，整個圖壓縮算法GC-W 的耗時為O(|V|+2|E|)。

3）在節(jié)點平均權(quán)值計算和子圖連通性判斷方面，假設(shè)圖壓縮的壓縮比為cr，則壓縮后節(jié)點和邊的數(shù)量大致可以表示為(cr)|V|和(cr)|E|。此外，由于節(jié)點和邊的數(shù)量減少，算法迭代的次數(shù)也會相應(yīng)減少。若壓縮前需要的迭代次數(shù)為t，則壓縮后需要的迭代次數(shù)大致為(cr)t。因此，節(jié)點平均權(quán)值的計算需要耗時O(t(|V|+|E|)(cr)2)。子圖連通性判斷使用的是廣度優(yōu)先搜索，所以耗時也為O(t(|V|+|E|)(cr)2)。

4）在子圖k核的維護方面，由于壓縮圖沒有保留原節(jié)點的度信息，因此查詢節(jié)點度的耗時沒有變，仍然為O(|E|)，算法需要迭代(cr)t次，則此步的總耗時為O(t(cr)|E|)。

5）在壓縮圖的解壓縮方面，由于壓縮算法GCW 會返回一個映射表M，M中記錄了原圖G中每個節(jié)點所對應(yīng)的超節(jié)點。借助M，可以在O(|V|)時間內(nèi)將壓縮后的圖解壓縮。

最終CRK-C 算法的時間復(fù)雜度為O(t(cr)m)，其中，t表示迭代次數(shù)，cr表示壓縮比，m表示原圖的邊數(shù)。

接下來分析CRK-C 算法的空間復(fù)雜度，由于該算法在CRK-G 算法的基礎(chǔ)上引入了圖壓縮過程，因此在計算過程中除了原有的空間消耗外，還需要額外存儲壓縮圖的信息，壓縮圖信息包括每個超節(jié)點的鄰節(jié)點和超邊的權(quán)值，假設(shè)圖壓縮的壓縮比為cr，則其空間消耗為O(2(cr)|E|)。原有的空間消耗為O(4|E|)，故CRK-C 算法的空間復(fù)雜度為O(m)。

4.1.3 CRK-C 算法的誤差分析

CRK-C 算法雖然提高了效率，但是其相對于CRK-G 算法存在一定的誤差。CRK-C 算法可能導(dǎo)致的誤差是其多迭代刪除的節(jié)點數(shù)。假設(shè)經(jīng)過壓縮算法壓縮后的壓縮比為cr，在壓縮圖中平均一個節(jié)點對應(yīng)原圖1/cr個節(jié)點。在最壞的情況下，某次迭代刪除中正常迭代刪除一個節(jié)點即可達到緊密k核子圖的要求，而由于采用的是壓縮圖進行迭代，則該次刪除的節(jié)點數(shù)為1/cr，誤差為(1/cr)-1 ＜1/cr，即CRK-C 算法的平均誤差小于1/cr，壓縮比cr越大則誤差越小。

需要說明的是，壓縮比cr取決于壓縮閾值θ的取值，θ和cr的具體關(guān)系則還要結(jié)合候選子圖中節(jié)點權(quán)值的情況。但若在同一個圖數(shù)據(jù)中，θ越大則會有更多的節(jié)點被合并，伴隨著壓縮比cr會越小。

4.2 基于單次多節(jié)點刪除的優(yōu)化策略

提高CRK-G 算法效率的改進策略除降低圖規(guī)模外，另一種方法是減少算法的迭代次數(shù)，而減少迭代次數(shù)的一個有效且直接的方法是批量刪除節(jié)點。通過在單次迭代中一次性刪除多個節(jié)點來減少迭代次數(shù)，從而提高算法的效率。

4.2.1 CRK-F 算法

基于單次多節(jié)點刪除策略，對CRK-G 算法進行改進，得到效率更高的快速貪婪算法CRK-F。CRKF 算法設(shè)置了每次迭代時的刪除比率γ，其中γ∈(0，1)。若候選子圖H的節(jié)點數(shù)為|V()H|，設(shè)迭代時刪除的節(jié)點集為S，則節(jié)點集S的數(shù)量|S|=γ|V(H)|。節(jié)點集S的取值是通過對每次迭代后剩余子圖的節(jié)點按節(jié)點權(quán)值進行排序，權(quán)值最小的前γ|V(H)|個節(jié)點組成的集合即為節(jié)點集S。在下一次迭代刪除時，S即作為需要從候選子圖中刪除的節(jié)點集。

需要說明的是，γ越大則每次迭代刪除的節(jié)點數(shù)就越多，總的迭代次數(shù)就越少，可能導(dǎo)致的誤差就越大。γ的參考取值可經(jīng)過計算得到，假設(shè)迭代刪除一個節(jié)點后，子圖的節(jié)點權(quán)值平均上升Δ-----Aw，則：

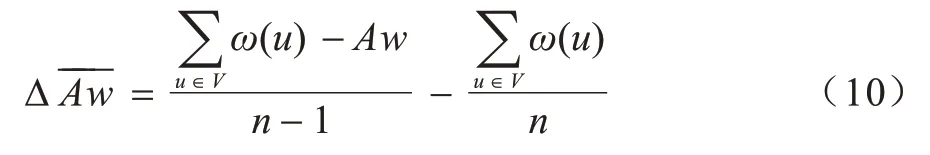
目標(biāo)節(jié)點平均權(quán)值wQ和當(dāng)前候選子圖的節(jié)點平均權(quán)值A(chǔ)w之間的差值ΔwQ=wQ-Aw，假設(shè)需要刪除K個節(jié)點后子圖節(jié)點平均權(quán)值為wQ，則：

而迭代刪除的節(jié)點數(shù)K=γ|V|，則：

在實際應(yīng)用時，式（12）可作為γ的取值依據(jù)。一般來講，取值時考慮目標(biāo)節(jié)點平均權(quán)值wQ和當(dāng)前候選子圖的節(jié)點平均權(quán)值A(chǔ)w之間的差值。當(dāng)差值較大時，γ取值可適當(dāng)增大，使其能更快地迭代到目標(biāo)值附近；反之，γ取值可適當(dāng)減小。

4.2.2 CRK-F 算法的復(fù)雜度分析

CRK-F 算法克服了CRK-G 算法效率低下的問題，通過利用單次多節(jié)點刪除的方法，極大地減少了算法的迭代次數(shù)，接下來對該算法進行時間復(fù)雜度與空間復(fù)雜度分析。

CRK-F 算法與CRK-G 算法相比，前者的迭代次數(shù)減少。首先分析改進后算法的迭代次數(shù)，初始時候選子圖H的節(jié)點數(shù)為|V(H)|≤|V(G)|，其中G為給定需要查詢的原圖。若每次迭代刪除的節(jié)點集為S，則經(jīng)過i次迭代后，|S|=γ|V(Hi)|，即此時節(jié)點集S將從剩余子圖Hi中刪除。這表明在經(jīng)過第i+1 次迭代后，剩余子圖Hi+1中至多有(1-γ)(|V(Hi)|)個節(jié)點，即假設(shè)需要進行t'次迭代后算法才結(jié)束，則：

CRK-F 算法與CRK-G 算法在空間上的消耗沒有區(qū)別，所以CRK-F 算法的空間復(fù)雜度也是O(m)。

4.2.3 CRK-F 算法的誤差分析

根據(jù)CRK-F 算法特點可知，其相對于CRK-G 算法的誤差是由于批量刪除時多刪除的節(jié)點導(dǎo)致。

假設(shè)給定刪除比率γ，當(dāng)算法迭代到第t次時結(jié)束，那么在t-1 次時候選子圖剩余的節(jié)點數(shù)為(1-γ)t-1(|V|)。隨后進行第t次迭代，在最壞情況下，本次迭代原本只需要刪除一個節(jié)點即可達到緊密k核子圖的要求，而由于采用批量刪除，實際刪除的節(jié)點數(shù)為(1-γ)t-1(|V|)γ，誤差為(1-γ)t-1(|V|)γ-1 ＜(1-γt-1(|V|)γ，即CRK-F 算法誤差不超過(1-γ)t-1(|V|)γ。

4.3 CRK-C 與CRK-F 算法對比分析

通過對CRK-C 與CRK-F 算法的原理分析，對兩者的特點總結(jié)如下：

1）CRK-C 算法使用了圖壓縮策略，通過將節(jié)點權(quán)值在閾值范圍內(nèi)的連通節(jié)點進行合并，從而降低子圖的規(guī)模，也相應(yīng)減少了迭代次數(shù)，算法效率相對CRK-G 算法而言有了較大的提升。根據(jù)算法的特點，若圖中節(jié)點權(quán)值較為相近時，節(jié)點壓縮策略將會起較大的作用。在節(jié)點壓縮時，更多節(jié)點權(quán)值相近的節(jié)點將會被合并，并且由于被合并的節(jié)點權(quán)值相近，其在迭代刪除過程中所造成的誤差也較小，因此CRK-C 算法更適用于圖中節(jié)點權(quán)值差異性較小的數(shù)據(jù)。

2）CRK-F 算法利用單次多節(jié)點刪除策略，每次迭代刪除多個節(jié)點，顯著減少了迭代次數(shù)。由于CRK-F 算法僅需要在迭代刪除時設(shè)置刪除比率γ，從而進行節(jié)點的批量刪除，其實現(xiàn)相較于CRK-C 算法而言更加簡單，效率提升也較為明顯。并且根據(jù)算法的特點，其誤差能夠較好地被預(yù)測，有利于控制算法的誤差。當(dāng)圖中節(jié)點權(quán)值差異性較大或無法確定差異性時，可優(yōu)先考慮使用CRK-F 算法。

5 實驗結(jié)果與分析

本文在3 個真實數(shù)據(jù)集上進行了實驗，對比了算法在不同查詢條件下和不同規(guī)模圖上查詢的耗時，并分析壓縮算法GC-W 和緊密k核子圖模型的有效性，最后結(jié)合實例進一步說明模型的優(yōu)越性。

5.1 數(shù)據(jù)集

本文實驗使用的數(shù)據(jù)集主要有以下3 個：

1）生物通用交互數(shù)據(jù)集Bio-GRID，其中節(jié)點表示基因或蛋白質(zhì)，邊表示基因或蛋白質(zhì)之間存在交互，邊的權(quán)值表示節(jié)點之間交互的得分，得分越高說明節(jié)點之間的聯(lián)系越緊密。

2）美國安然公司的郵件網(wǎng)絡(luò)Email-Enron，其中頂點表示郵箱，邊表示一個郵箱向另一郵箱發(fā)送過郵件，邊的權(quán)值表示郵箱之間郵件的互通次數(shù)，次數(shù)越高說明郵箱之間的聯(lián)系越緊密。

3）由DBLP 數(shù)據(jù)構(gòu)成的作者協(xié)作網(wǎng)絡(luò)，其中節(jié)點表示作者，邊表示兩個作者共同合作發(fā)表過文章，邊的權(quán)值表示作者合作過的次數(shù)，次數(shù)越高說明作者之間的聯(lián)系越緊密。

上述數(shù)據(jù)集經(jīng)預(yù)處理轉(zhuǎn)化為圖數(shù)據(jù)，各個圖的基本特性如表1 所示。其中：節(jié)點數(shù)和邊數(shù)反映了圖的規(guī)模；最大核值為k核分解后圖中節(jié)點最大的核值，反映了圖中最稠密社團的稠密度；平均核值反映了圖整體的稠密程度；節(jié)點平均權(quán)值反映了圖節(jié)點之間整體聯(lián)系的緊密程度。

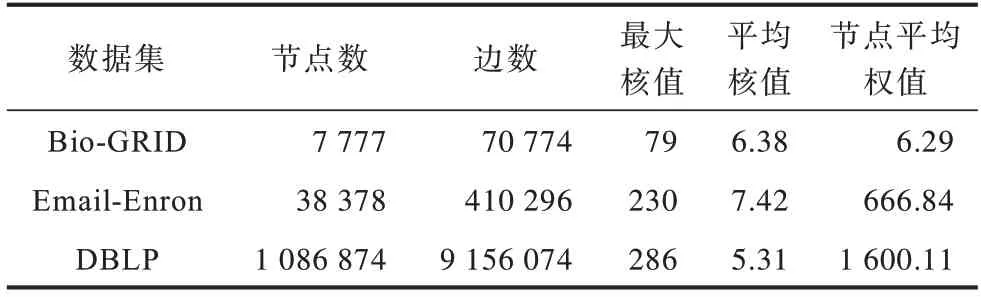
表1 數(shù)據(jù)集的基本特性Table 1 Basic characteristics of dataset

5.2 實驗分析

本文在上述3 個數(shù)據(jù)集上進行實驗，對比了算法CRK-G、CRK-C、CRK-F 在不同條件下的查詢效率和圖壓縮算法GC-W 的壓縮效率，并驗證了模型的有效性。實驗使用C++實現(xiàn)，在2.90 GHz Intel?CoreTMi5-9400 CPU、8.0 GB 內(nèi)存、Windows10 系統(tǒng)的臺式機上運行。

5.2.1 算法效率分析

在查詢緊密k核子圖時，需要給定核值k和節(jié)點平均權(quán)值wQ。為驗證算法的效率，本文設(shè)計了控制變量的對比實驗，記錄3 個算法隨著給定值變化時其查詢所消耗的時間。在下文實驗中，CRK-C 算法的壓縮閾值θ=0.01，CRK-F 算法的刪除比率γ=0.1。

由于查詢參數(shù)的取值不是本文的研究重點，實驗中的參數(shù)值是通過前期的初步實驗并結(jié)合數(shù)據(jù)集的特性得到。其中，參數(shù)wQ的給定是通過初步的實驗，大致計算得到各個數(shù)據(jù)集子圖的最大節(jié)點平均權(quán)值，將該值取整十或整百，然后等差遞減得到wQ的取值范圍。在實際應(yīng)用中可以根據(jù)對子圖緊密程度的需求來選擇核值k和節(jié)點平均權(quán)值wQ，以及對誤差允許的范圍來選擇合適的壓縮閾值θ和刪除比率γ。

本文分別控制k和wQ的變化，在3 個數(shù)據(jù)集上進行以下兩組實驗：

1）隨著給定節(jié)點平均權(quán)值wQ的變化，實驗并記錄在3 個數(shù)據(jù)集上算法CRK-G、CRK-C、CRK-F 查詢所需要的時間。對于數(shù)據(jù)集Bio-GRID，給定k=20，變量wQ的取值范圍為{20，30，40，50，60}；對于數(shù)據(jù)集Email-Enron，給定k=30，變量wQ的取值范圍為{9 000，10 000，11 000，12 000，13 000}；對于數(shù)據(jù)集DBLP，給定k=40，變量wQ的取值范圍為{200，225，250，275，300}。

3 種算法隨wQ變化的運行效率對比結(jié)果如圖4所示，隨著節(jié)點平均權(quán)值wQ增大，各算法在不同數(shù)據(jù)集上的查詢耗時總體均增加。之所以如此，是因為當(dāng)給定節(jié)點平均權(quán)值wQ增大時，算法所需要的迭代次數(shù)增多，故耗時增加。在3 種算法的效率對比中，CRK-G 算法的查詢耗時明顯高于另兩種算法。在Bio-GRID 數(shù)據(jù)集上，CRK-C 算法的速度略快于CRK-F 算法，通過對數(shù)據(jù)集特性的分析，發(fā)現(xiàn)Bio-GRID 數(shù)據(jù)集中存在較多權(quán)值相近的節(jié)點，使得該數(shù)據(jù)集的候選子圖經(jīng)過壓縮后的壓縮比較低，故CRKC 算法的查詢速度較快。反之，在DBLP 數(shù)據(jù)集上，CRK-F 算法速度快于CRK-C 算法是由于該數(shù)據(jù)集上權(quán)值相近的節(jié)點較少。

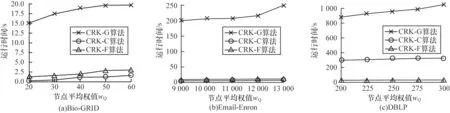
圖4 3 種算法隨wQ 變化的運行效率對比Fig.4 Comparison of the operating efficiency of the three algorithms with the change of wQ

2）隨著給定核值k的變化，實驗并記錄在3 個數(shù)據(jù)集上算法CRK-G、CRK-C、CRK-F 查詢所需要的時間。對于數(shù)據(jù)集Bio-GRID，給定wQ=40，變量k的取值范圍為{10，15，20，25，30}；對于數(shù)據(jù)集Email-Enron，給定wQ=11 000，變量k的取值范圍為{10，20，30，40，50}；對于數(shù)據(jù)集DBLP，給定wQ=250，變量k的取值范圍為{20，30，40，50，60}。

3 種算法隨k變化的運行效率對比結(jié)果如圖5 所示，隨著核值k增大，各算法在不同數(shù)據(jù)集上的查詢耗時總體均減少。之所以如此，是因為當(dāng)給定核值k增大時，得到的候選k核子圖規(guī)模減小，算法迭代次數(shù)減少，故耗時減少。另外，在3 種算法的效率對比中，當(dāng)k值較小時，CRK-G 算法的查詢耗時明顯高于另兩種算法。

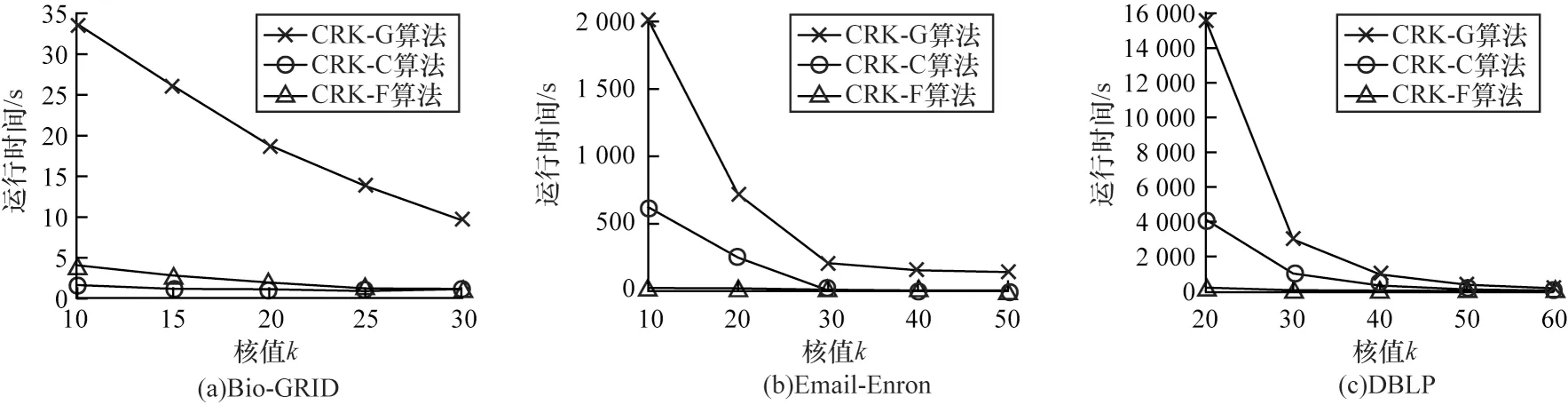
圖5 3 種算法隨k 變化的運行效率對比Fig.5 Comparison of the operating efficiency of the three algorithms with the change of k

上述實驗結(jié)果與本文對各個算法的時間復(fù)雜度分析結(jié)果相符合，CRK-G 算法的查詢耗時總體均高于CRK-C 和CRK-F 算法。而CRK-C 算法和CRK-F算法兩者耗時大致相近，具體耗時高低主要取決于數(shù)據(jù)集的特點，當(dāng)數(shù)據(jù)集中存在較多權(quán)值相近的節(jié)點時，圖壓縮算法壓縮后得到的圖規(guī)模較小，使得CRK-C 算法的查詢耗時低于CRK-F 算法。

5.2.2 算法誤差分析

由于CRKSQ 問題是NP-難的，無法在多項式時間復(fù)雜度內(nèi)找到最優(yōu)解，CRK-G 算法雖然能夠找到一個可行解，但其與最優(yōu)解之間的偏離程度無法被預(yù)計。CRK-C 和CRK-F 算法是在CRK-G 算法基礎(chǔ)上的改進，效率有了很大的提升，但兩者相對于CRK-G 算法存在一定的誤差。接下來以CRK-G 算法為參考，在不同k值條件下，對CRK-C 和CRK-F 算法查詢結(jié)果的誤差進行分析。

根據(jù)算法的原理，評判誤差的依據(jù)是CRK-C 和CRK-F算法相對于CRK-G算法是否過多刪除了節(jié)點。實驗在3 個數(shù)據(jù)集上進行：對于數(shù)據(jù)集Bio-GRID，給定wQ=40，變量k的取值范圍為{10，15，20，25，30}；對于數(shù)據(jù)集Email-Enron，給定wQ=11 000，變量k的取值范圍為{10，20，30，40，50}；對于數(shù)據(jù)集DBLP，給定wQ=250，變量k的取值范圍為{20，30，40，50，60}。

實驗記錄了各個算法在上述條件下查詢得到的子圖節(jié)點數(shù)，計算了CRK-C 和CRK-F 算法相對于CRK-G 算法的誤差百分比，結(jié)果分別如表2～表4 所示，多次實驗的平均誤差均在8%以內(nèi)，誤差較小。

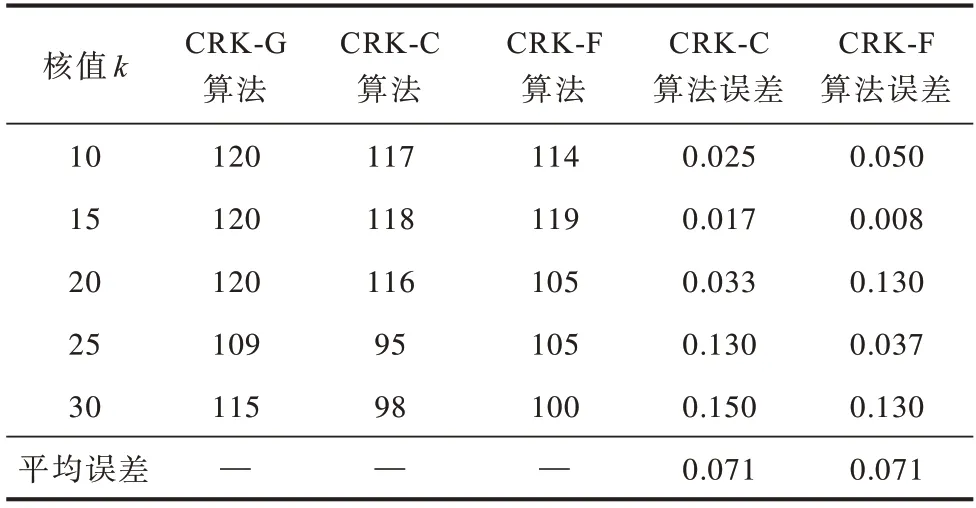
表2 Bio-GRID 數(shù)據(jù)集的查詢結(jié)果與誤差Table 2 Query results and errors of Bio-GRID dataset

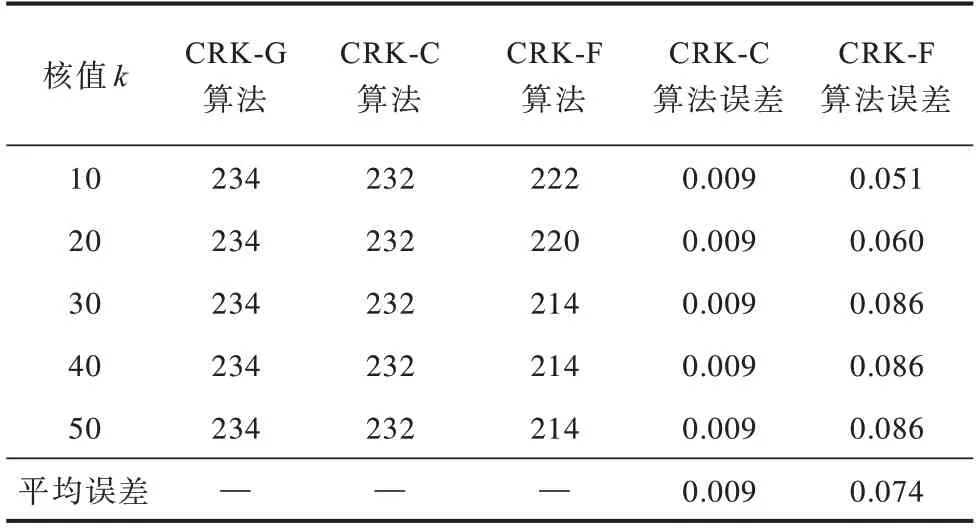
表3 Email-Enron 數(shù)據(jù)集的查詢結(jié)果與誤差Table 3 Query results and errors of Email-Enron dataset

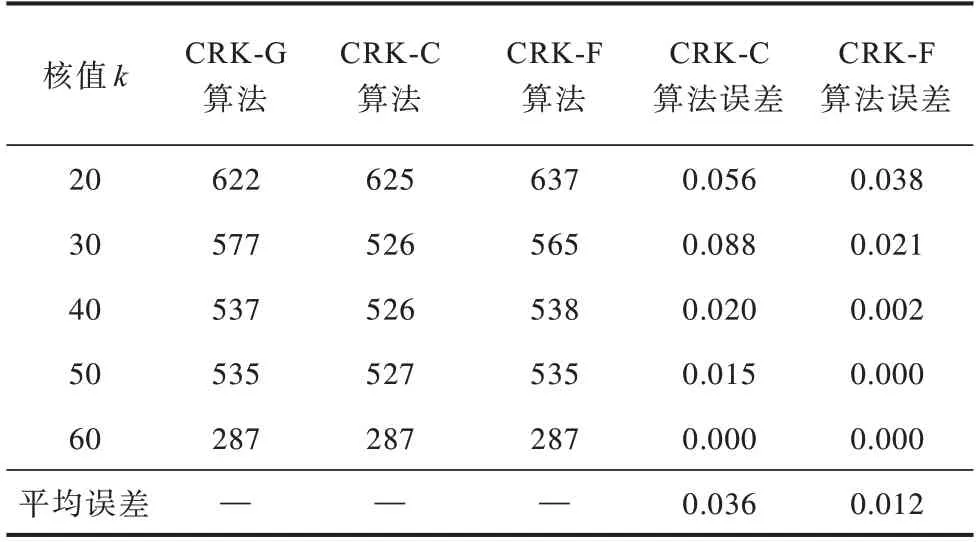
表4 DBLP 數(shù)據(jù)集的查詢結(jié)果與誤差Table 4 Query results and errors of DBLP dataset

5.2.3 圖壓縮算法有效性分析

為驗證圖壓縮算法GC-W 的有效性，實驗記錄了不同k值條件下，GC-W 算法在3 個數(shù)據(jù)集上壓縮候選子圖的耗時。

對于數(shù)據(jù)集Bio-GRID，變量k的取值范圍為{10，15，20，25，30}；對于數(shù)據(jù)集Email-Enron，變量k的取值范圍為{10，20，30，40，50}；對于數(shù)據(jù)集DBLP，變量k的取值范圍為{20，30，40，50，60}。實驗結(jié)果如圖6所示，當(dāng)k值增大時，壓縮時間減少。由于當(dāng)k值增大時候選k核子圖的規(guī)模減小，因此壓縮算法GC-W 的耗時減少。

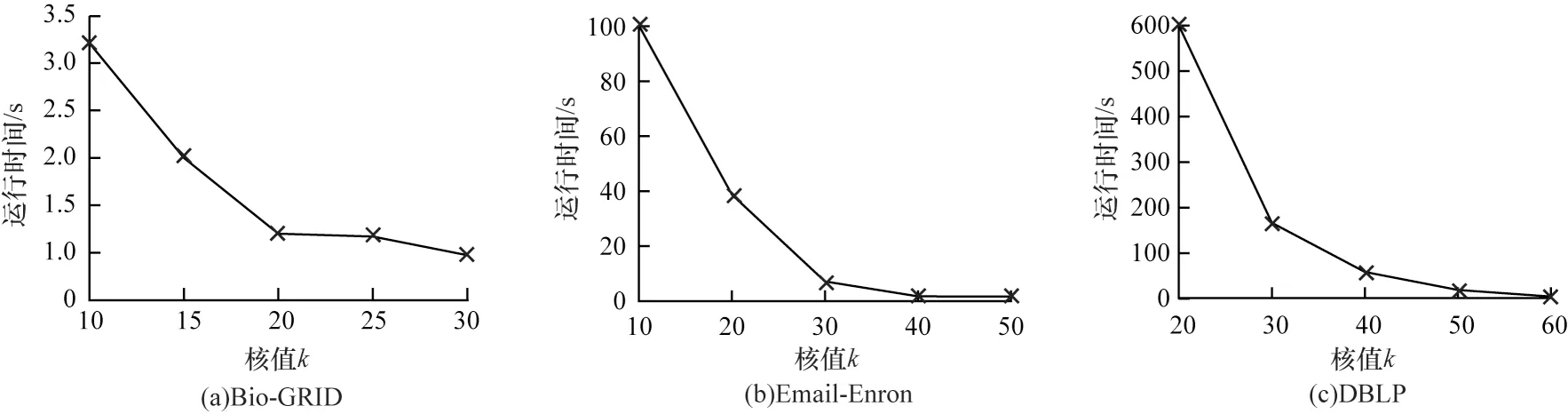
圖6 GC-W 算法隨k 變化的壓縮耗時Fig.6 Compression time of GC-W algorithm with the change of k

壓縮耗時相較于查詢耗時低了1 或2 個數(shù)量級，其可以在相對短的時間內(nèi)對候選子圖進行壓縮，有效地減少了查詢時間，壓縮算法是有效的。

5.2.4 模型有效性分析

為驗證緊密k核子圖（CRKS）模型的有效性，本文實驗對比了CRK-F 算法與忽略權(quán)值的k核（k-core）算法，記錄兩者在不同k值條件下查詢得到的子圖節(jié)點平均權(quán)值。

實驗分別在3 個數(shù)據(jù)集上進行，考慮到CRK-F算法和k-core 算法每次查詢得到的子圖都有可能存在多個，并且前者會由于給定的wQ不同而得到不同的結(jié)果。因此，本文將CRK-F 算法在不同wQ條件下查詢得到的子圖最大節(jié)點平均權(quán)值與k-core 算法查詢得到的所有子圖最大節(jié)點平均權(quán)值進行對比。

對于數(shù)據(jù)集Bio-GRID，變量k的取值范圍為{10，15，20，25，30}；對于數(shù)據(jù)集Email-Enron，變量k的取值范圍為{10，20，30，40，50}；對于數(shù)據(jù)集DBLP，變量k的取值范圍為{20，30，40，50，60}。實驗結(jié)果 如圖7 所示。從實驗結(jié)果可以看出，CRK-F 算法得到的子圖節(jié)點平均權(quán)值均大于k-core 算法，驗證了CRKS 模型的有效性和優(yōu)越性。

圖7 CRK-F與k-core 算法的子圖節(jié)點平均權(quán)值對比Fig.7 Comparison of average weights of subgraph nodes obtained between CRK-F and k-core algorithms

5.2.5 實例分析

為進一步說明CRKS 模型的合理性，本文選取一個實例進行分析。圖8（a）所示是作者協(xié)作網(wǎng)絡(luò)中選取的部分?jǐn)?shù)據(jù)，其包含了30 個節(jié)點和46 條邊，圖的節(jié)點平均權(quán)值為40.67，存在一些聯(lián)系較為松散的節(jié)點。若忽略權(quán)值，僅給定k=3，進行3 核查詢，查詢結(jié)果如圖8（b）所示。從圖中可以看出，雖然所有節(jié)點的度均大于等于3，對應(yīng)著至少3 個鄰接節(jié)點，但結(jié)合邊的權(quán)值就可發(fā)現(xiàn)節(jié)點“Bin Zhou”所對應(yīng)的權(quán)值較小，該節(jié)點將左右兩部分的圖連接成一體，使得圖整體結(jié)構(gòu)并不緊湊，左右兩部分節(jié)點之間聯(lián)系的緊密程度不足。若考慮權(quán)值，給定wQ=50，對圖8（a）所示的圖進行緊密3 核子圖查詢，得到圖8（c）所示的結(jié)果。該結(jié)果包含兩個子圖，每個圖相較于圖8（b），內(nèi)聚性更強，節(jié)點之間的聯(lián)系也更加緊湊。兩個子圖的節(jié)點平均權(quán)值分別為50.8 和53.2，相較于圖8（b）的47.08，兩個子圖整體的聯(lián)系也更加緊密。

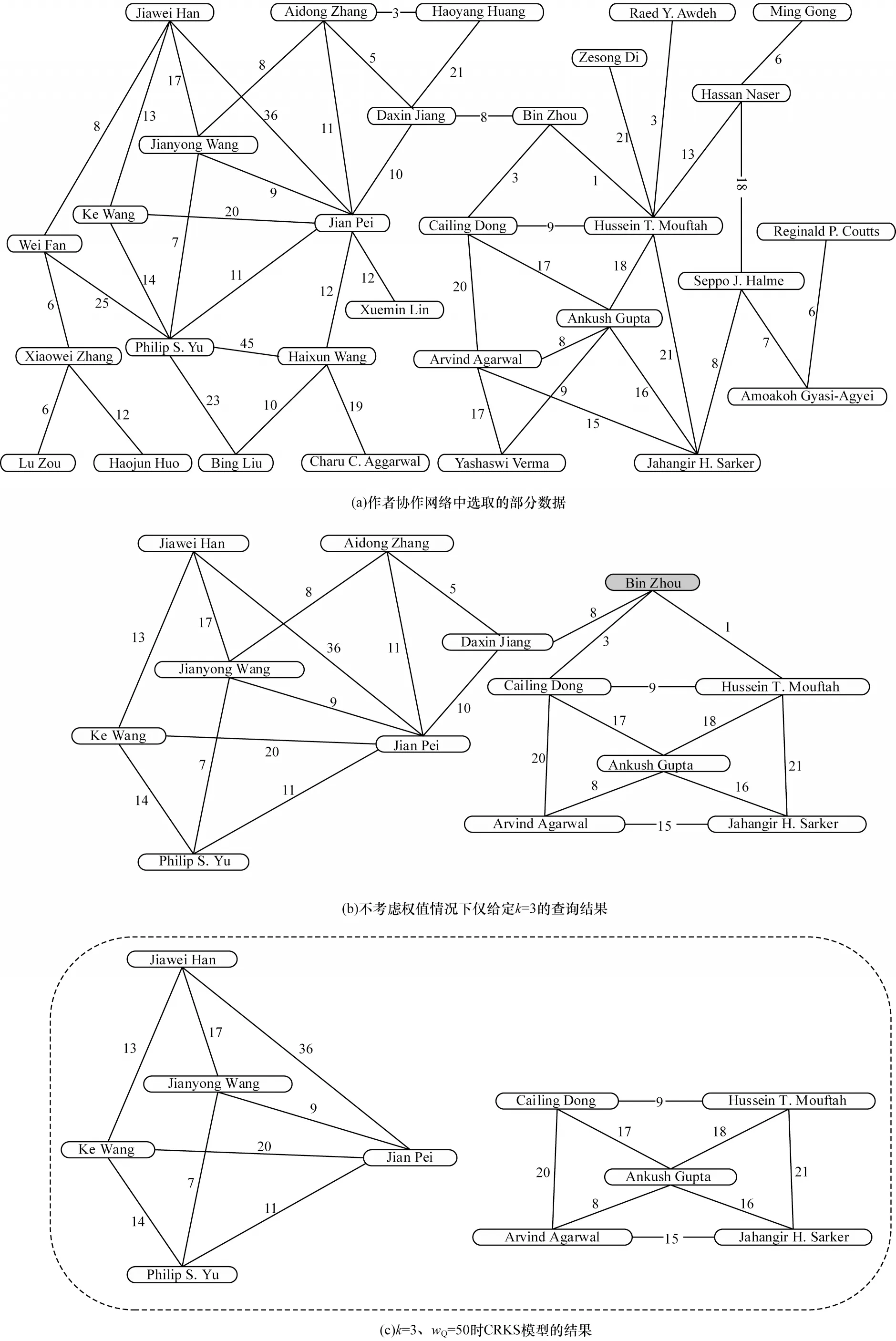
圖8 緊密k 核子圖的查詢實例分析結(jié)果Fig.8 Query example analysis results of closely related k-core subgraph

綜合上述分析，CRKS 模型可以檢測出加權(quán)圖中緊密聯(lián)系的子圖，相較于現(xiàn)有的方法更加合理有效。

6 結(jié)束語

本文提出一種在加權(quán)圖中查詢聯(lián)系緊密的連通k核子圖問題，并證明了該問題是NP-難的。為解決CRKSQ 問題，設(shè)計基于貪婪策略的啟發(fā)式算法CRK-G，其能在可接受的時間內(nèi)為CRKSQ 問題找到一個近似解，分別從降低圖規(guī)模和減少迭代次數(shù)兩個方面出發(fā)，提出兩個改進算法CRK-C 和CRK-F，其在查詢速度上有明顯提升。在不同規(guī)模數(shù)據(jù)集上進行多次實驗，結(jié)果表明，CRK-C 和CRK-F 算法的平均誤差都在8%以內(nèi)。下一步將研究本文算法參數(shù)的取值和優(yōu)化問題，并探索其他更加高效的緊密k核子圖查詢算法，以滿足超大圖的查詢要求。