基于SFPN的軌道交通車門故障診斷方法研究

覃 語,徐永能

(南京理工大學(xué) 自動化學(xué)院， 南京 210094)

1 引言

軌道交通作為現(xiàn)代化社會中最重要的交通工具之一，在緩解交通堵塞和促進(jìn)城市發(fā)展方面扮演著重要角色。隨著時代的發(fā)展，城市軌道交通的客運壓力不斷增大，車門系統(tǒng)作為軌道車輛中結(jié)構(gòu)最復(fù)雜、涉及零部件最多的系統(tǒng)，其故障頻率也隨著使用率的升高而不斷增大，嚴(yán)重影響了列車運行的安全性和可靠性。因此，需要一種準(zhǔn)確、適用性高的車門系統(tǒng)故障診斷方法，以快速確定故障部件，提高檢修效率，進(jìn)而保障地鐵高效安全運行。

對于車門故障診斷的相關(guān)研究，常用到的理論方法包括人工神經(jīng)網(wǎng)絡(luò)、專家系統(tǒng)、貝葉斯網(wǎng)絡(luò)、Petri網(wǎng)理論等。其中，Petri網(wǎng)模型法具有數(shù)學(xué)邏輯嚴(yán)謹(jǐn)、物理意義明確、邏輯推理清晰等優(yōu)點，適用于復(fù)雜的車門故障分析。該方法不僅可以快速判斷發(fā)生的故障類型，還可以追溯故障發(fā)生線路，快速定位到故障發(fā)生點。Yaung等基于傳統(tǒng)Petri網(wǎng)理論引入了FPR權(quán)重的概念。在此基礎(chǔ)上，針對多因果式網(wǎng)絡(luò)結(jié)構(gòu)，Ha等在權(quán)重FPR模型中引入輸入權(quán)重、輸出權(quán)重，提出了FPN模型。Liu等針對已有FPN模型提出了動態(tài)自適應(yīng)模糊Petri網(wǎng)。該并行推理算法基于極大代數(shù)，可以結(jié)合專家系統(tǒng)動態(tài)完成邏輯推理。

傳統(tǒng)模糊Petri網(wǎng)模型(TFPN)對于故障現(xiàn)象僅用隸屬度一個參數(shù)來描述。但根據(jù)以往的工作經(jīng)驗得知，故障事件的發(fā)生還常伴隨著不確定性，TFPN模型法卻無法對此進(jìn)行量化。本文中分析了現(xiàn)有車門故障模式及其影響，提出了一種基于球型模糊Petri網(wǎng)的地鐵車門系統(tǒng)故障診斷模型。該模型能夠更全面地評估故障事件發(fā)生的可能性，給出更可靠的故障傳播路徑推理結(jié)果，從而有效提升車門系統(tǒng)的安全性和可靠性。

2 車門故障分析

2.1 工作原理

車門系統(tǒng)結(jié)構(gòu)復(fù)雜，車門的開啟、關(guān)閉動作主要由電氣控制模塊、車門控制單元EDCU模塊及機(jī)械動作模塊3個模塊來實現(xiàn)。電氣控制模塊與機(jī)械動作模塊之間通過電子門控制器EDCU連接。電氣控制模塊負(fù)責(zé)將控制臺發(fā)出的開門信號、零速信號、驅(qū)動電機(jī)運轉(zhuǎn)信號等信息傳遞給電子門控制器EDCU。EDCU與電機(jī)之間產(chǎn)生交互信息，傳遞車門運動速度信號至機(jī)械運動模塊。三者關(guān)聯(lián)交互工作，共同控制車門系統(tǒng)的開關(guān)動作。車門系統(tǒng)結(jié)構(gòu)原理如圖1所示。

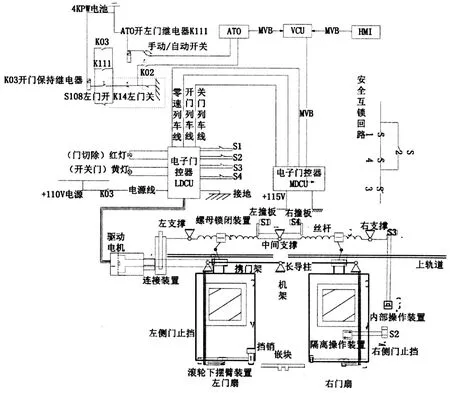
圖1 車門系統(tǒng)結(jié)構(gòu)原理示意圖Fig.1 Door system structure

當(dāng)需要開啟車門時，車輛控制中心會向車門系統(tǒng)發(fā)送零速信號。列車如果處于自動駕駛模式(ATO)時將會自動將零速信號、開門信號傳至EDCU。EDCU進(jìn)而輸出電信號驅(qū)動電機(jī)，通過電機(jī)帶動機(jī)械動作模塊來完成開門動作。當(dāng)需要關(guān)閉車門時，EDCU同樣會將從車輛控制中心收到的關(guān)門信號轉(zhuǎn)為驅(qū)動電機(jī)運作的電信號。車門關(guān)好后，鎖閉行程開關(guān)S1閉合，EDCU接收到車門關(guān)閉信號后傳遞給制動單元，制動單元對車門進(jìn)行制動反饋，車門的止擋、嵌塊、擋銷等部件將會配合完成對車門的鎖緊固定。工作流程如圖2所示。

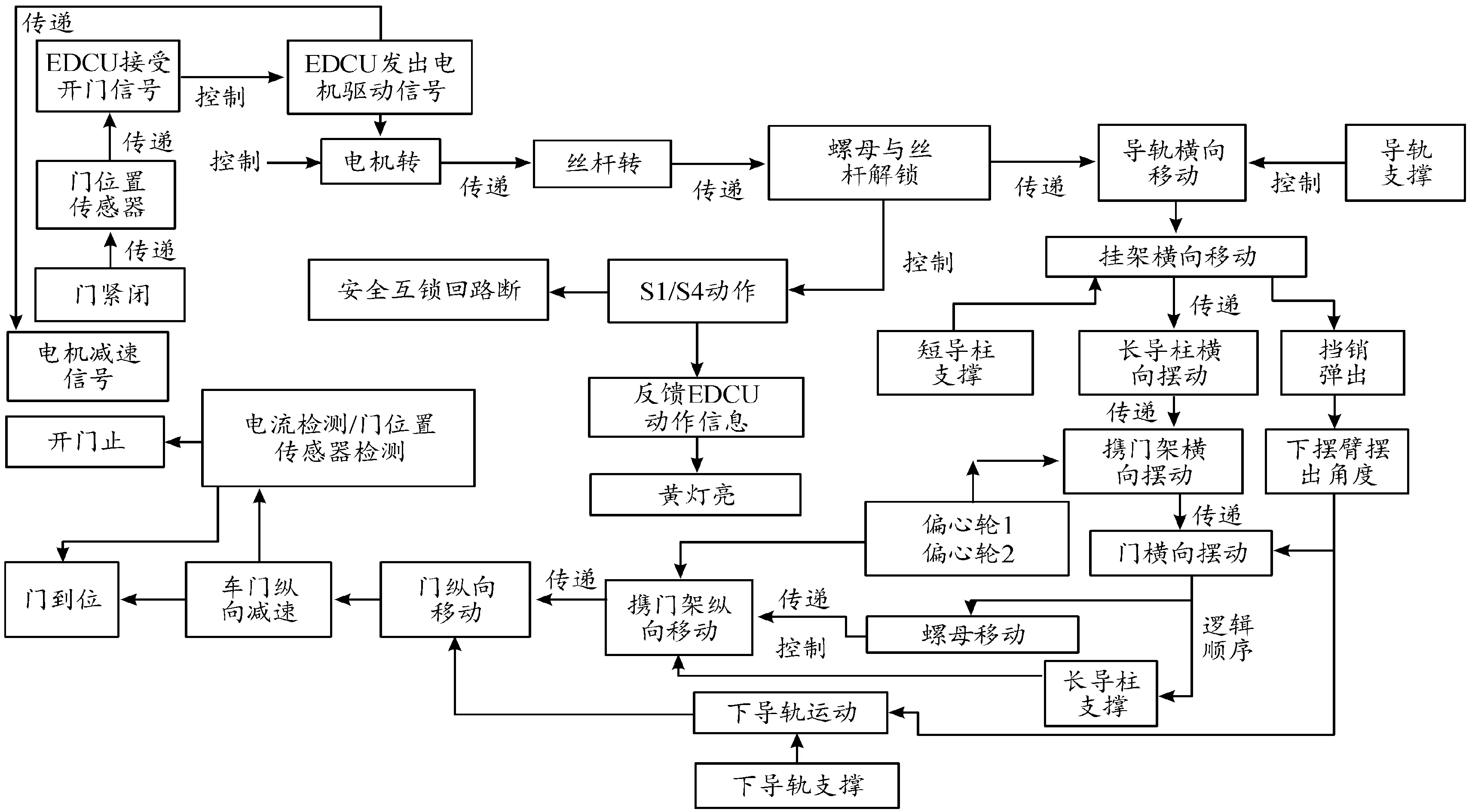
圖2 車門系統(tǒng)工作流程Fig.2 Door system workflow

2.2 故障模式分析

根據(jù)軌道交通車輛運行經(jīng)驗，總結(jié)了6種典型車門故障模式：車門自動開關(guān)門故障、車門開門故障、車門關(guān)門故障、車門指示燈故障、開關(guān)門動作異響、車門操作裝置故障。根據(jù)表1中故障樹相關(guān)符號規(guī)則，建立車門系統(tǒng)故障模式故障樹示意圖。

表1 故障樹事件符號和邏輯門符號Table 1 Fault event symbol and logic gate symbol

建立車門系統(tǒng)故障模式故障樹示意圖，如圖3—圖10所示。

圖3 頂事件故障樹Fig.3 Top event fault tree

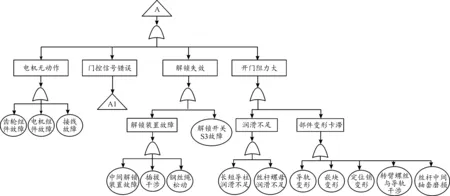
圖4 車門開門故障樹Fig.4 Door opening fault tree

圖5 車門開門故障樹子樹Fig.5 Door opening fault tree subtree

圖6 車門關(guān)門故障樹Fig.6 Door closing fault tree

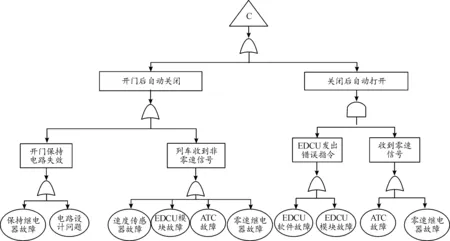
圖7 車門自動開關(guān)門故障樹Fig.7 Automatic door opening and closing fault tree

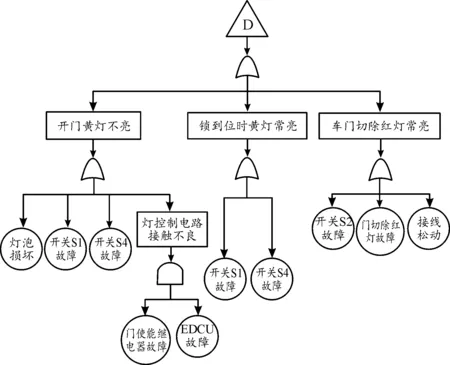
圖8 車門指示燈故障樹Fig.8 Door indicator fault tree

圖9 開關(guān)門動作異響故障樹Fig.9 Fault tree of abnormal sound caused by door opening and closing

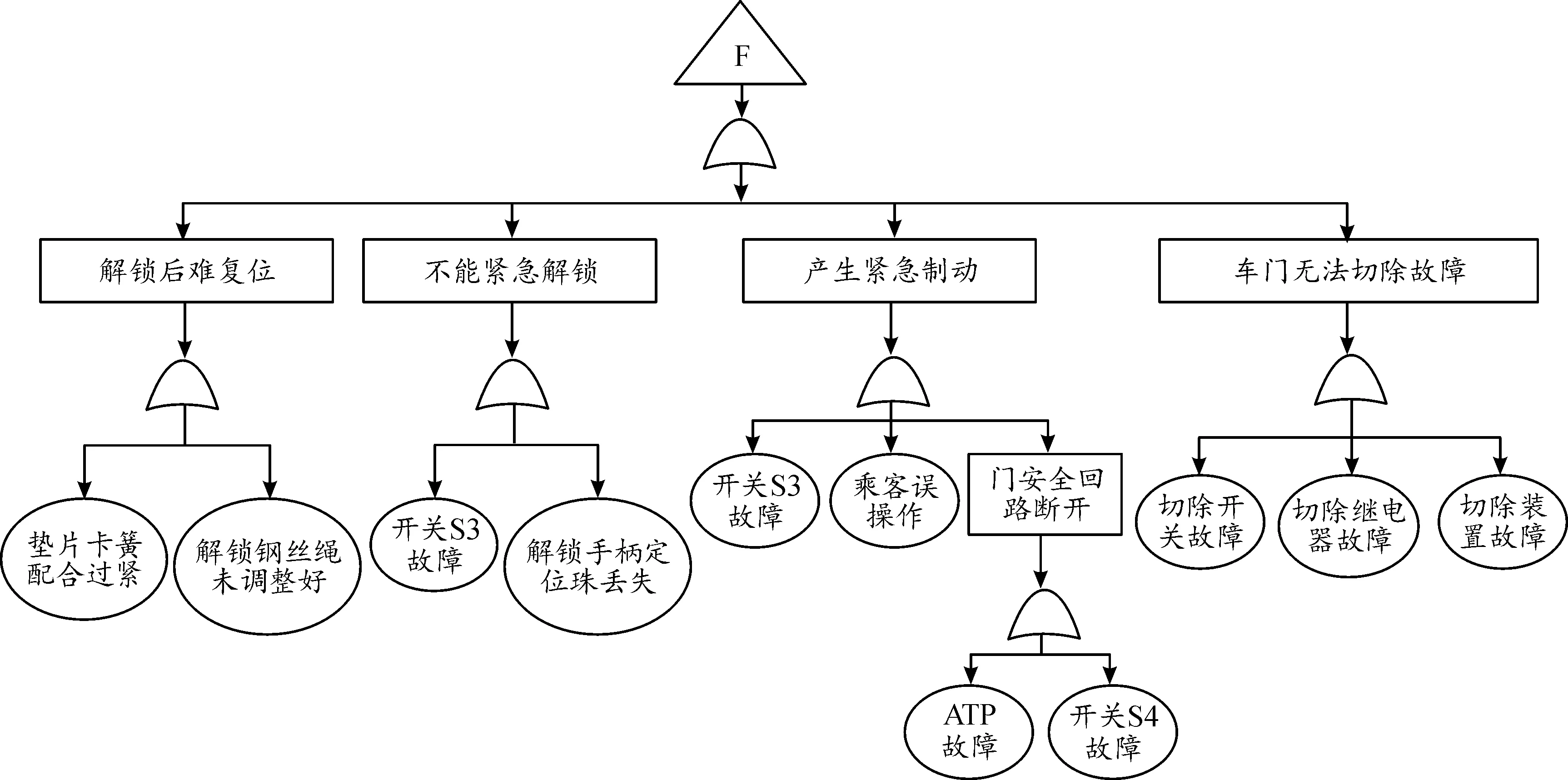
圖10 車門操作裝置故障樹Fig.10 Fault tree of door operating device

3 車門故障診斷方法

3.1 球型模糊Petri網(wǎng)模型

Petri網(wǎng)是20世紀(jì)60年代由卡爾·A·佩特里發(fā)明的一種用于描述異步、高并發(fā)復(fù)雜系統(tǒng)的網(wǎng)狀結(jié)構(gòu)信息流模型。它既有嚴(yán)格的數(shù)學(xué)表達(dá)式，也有清晰明確的圖形表達(dá)方法。為了更好地實現(xiàn)Petri網(wǎng)對現(xiàn)實世界系統(tǒng)的描述，Chen等基于事件的不確定性提出了模糊Petri網(wǎng)的概念。

球型模糊Petri網(wǎng)理論基于“球型模糊集”的概念，引入了“中立度”的概念。根據(jù)過往的故障維修及記錄經(jīng)驗，中立度可以更好地描述專家及檢修人員對故障模式的猶豫性。球型模糊Petri網(wǎng)可以定義為一個11元組：

(1)

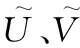
模糊Petri網(wǎng)中庫所與變遷的交互關(guān)系如圖11所示。“○”表示庫所，“|”表示變遷，“●”表示Token，如果一個庫所中含有一個Token，則證明此庫所代表的狀態(tài)正在發(fā)生。變遷與庫所之間通過箭頭“→”連接，表示變遷及其觸發(fā)閾值的信度值。

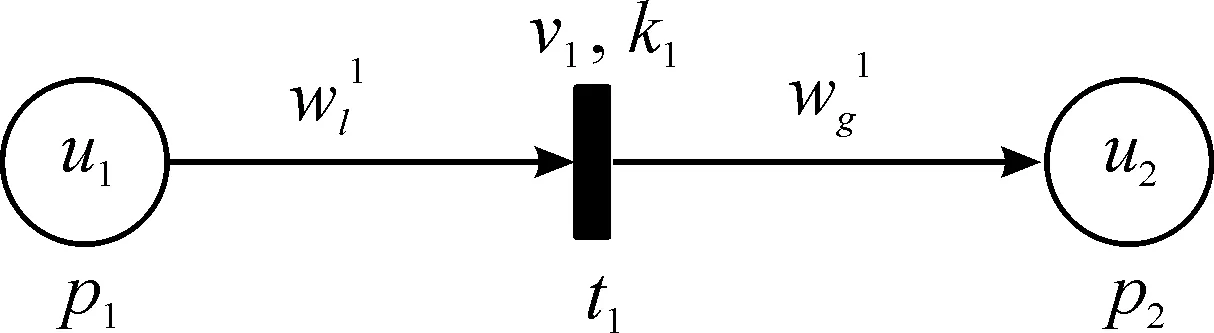
圖11 模糊Petri網(wǎng)模型Fig.11 Fuzzy Petri net model

車門系統(tǒng)故障與Petri網(wǎng)模型的結(jié)構(gòu)映射關(guān)系如表2所示。

表2 車門系統(tǒng)故障與模糊Petri網(wǎng)模型映射關(guān)系Table 2 Mapping relationship between vehicle door failure and fuzzy Petri net model

3.2 建立車門故障Petri網(wǎng)模型

根據(jù)文獻(xiàn)[13]，車門典型故障模式包括車門開/關(guān)門故障、車門自動開關(guān)門故障、指示燈故障、開關(guān)門動作異響。根據(jù)圖3～圖10的故障樹圖示可以確定基本故障事件和上層故障模式類型及從屬關(guān)系，如表3所示。

表3 故障事件與狀態(tài)表Table 3 Event and status

續(xù)表(表3)

續(xù)表(表3)

根據(jù)表3的信息即可得出故障演變發(fā)生的路徑及邏輯關(guān)系，進(jìn)而可得到如圖4所示的Petri網(wǎng)模型圖。由于整體Petri網(wǎng)模型圖過于復(fù)雜，僅展示“車門開門故障”、“車門關(guān)門故障” 的Petri網(wǎng)模型圖為例。

圖12中的結(jié)構(gòu)關(guān)系均為“或”關(guān)系，未體現(xiàn)和事件中“與”關(guān)系邏輯狀態(tài)。如“燈控制電路接觸不良”的上一狀態(tài)為 “+”，如圖13所示。

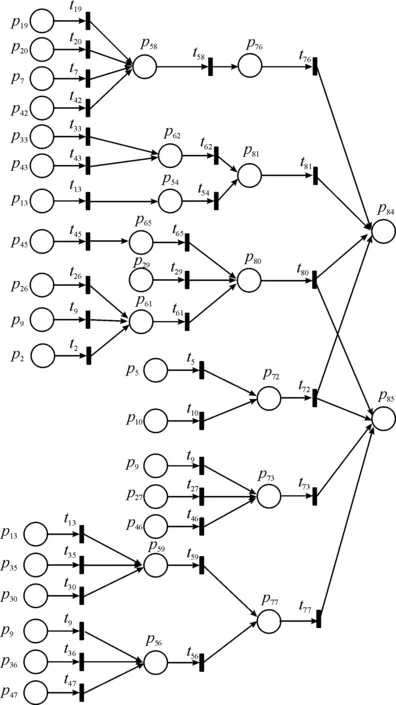
圖12 p84、p85車門故障模式球型Petri網(wǎng)模型示意圖Fig.12 The spherical Petri net model diagram of the door failure mode of events 84 and 85

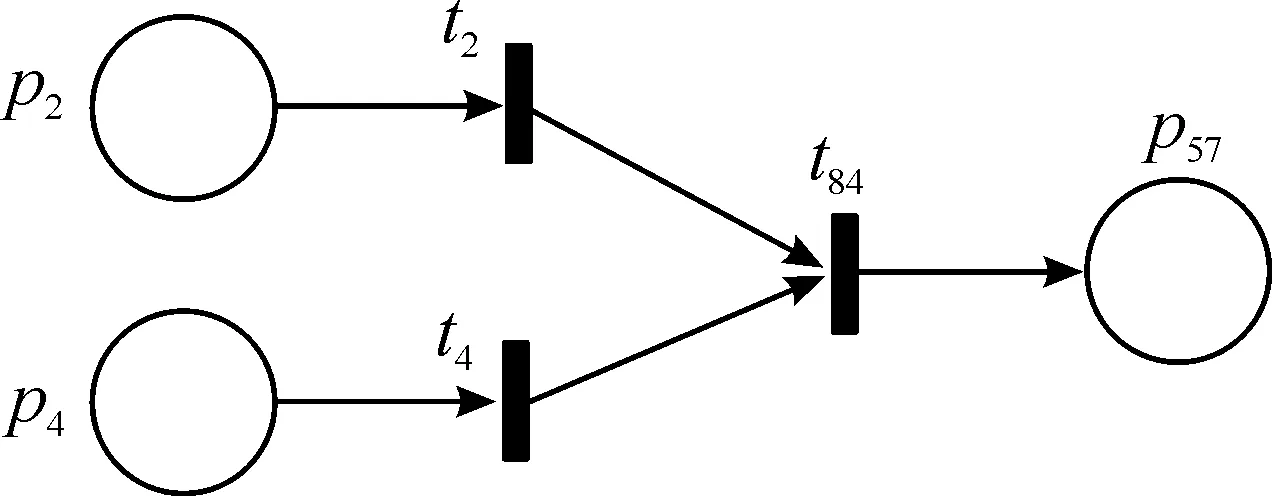
圖13 Petri網(wǎng)模型“與”關(guān)系示意圖Fig.13 Representation of “AND” relation in Petri net model

3.3 SFPN模型計算方法

對于日常監(jiān)測的設(shè)備，隸屬度不變，按照“中立度：非隸屬度：不確定度”的比例進(jìn)行模糊數(shù)據(jù)轉(zhuǎn)化，有關(guān)規(guī)則如表4所示。

表4 模糊轉(zhuǎn)化規(guī)則Table 4 Fuzzy transformation rule

對于不定期檢修的設(shè)備，根據(jù)其易發(fā)性評級標(biāo)準(zhǔn)進(jìn)行球型模糊數(shù)取值，如表5所示。

表5 部分設(shè)備易發(fā)性及其模糊數(shù)取值Table 5 Part of equipment’s susceptibility and its fuzzy number value

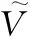
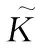
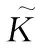
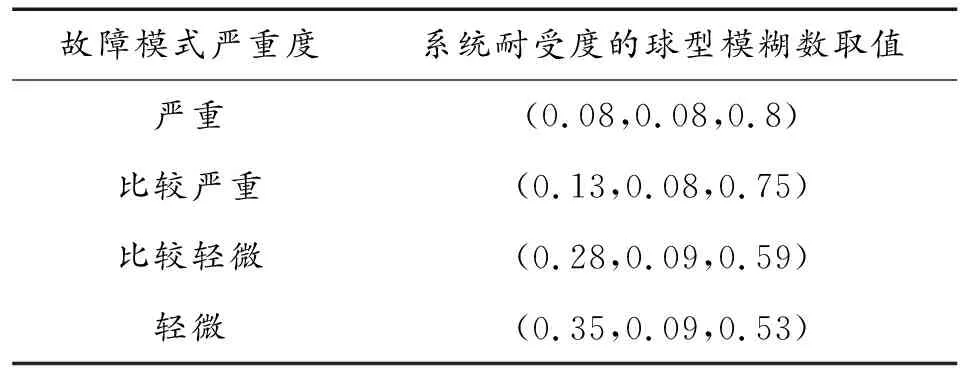
表6 變遷閾值判別規(guī)則Table 6 Criterion of transition threshold

4) 庫所與變遷見有向弧權(quán)重(、)

、為庫所輸入變遷的權(quán)重，為變遷輸出庫所的權(quán)重。假設(shè)各有向弧權(quán)重相等，且權(quán)重總和為1。

5) 模型計算

① 計算初始庫所狀態(tài)：根據(jù)式(2)判斷變遷是否會發(fā)生，得到庫所狀態(tài)矩陣

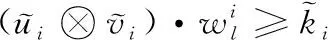
(2)

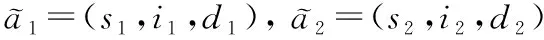
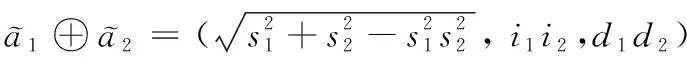
(3)

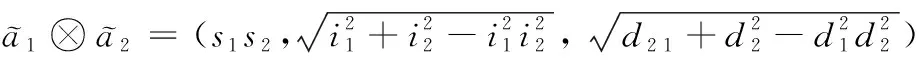
(4)

② 基于輸入矩陣計算輸入庫所信度值

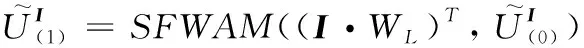
(5)

(6)

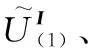
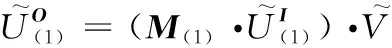
(7)

④ 更新所有庫所信度值

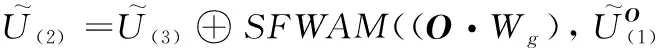
(8)

不斷迭代計算，直至庫所信度值不再變化，即得到所有故障事件的最終信度值。

4 SFPN車門故障診斷模型優(yōu)化驗證

4.1 初始庫所、變遷及變遷閾值信度值計算

由于篇幅限制，僅以車門開門故障模式為例進(jìn)行模型求解。

1) 初始庫所信度值

根據(jù)3.3節(jié)及表4、表5給出的計算規(guī)則，得到各庫所初始信度值如表7所示。

表7中～并非基礎(chǔ)故障事件，因此初始信度值為0，中立度為0，非隸屬度為1。

表7 車門開門故障庫所初始信度值Table 7 Initial reliability value of door opening failure database

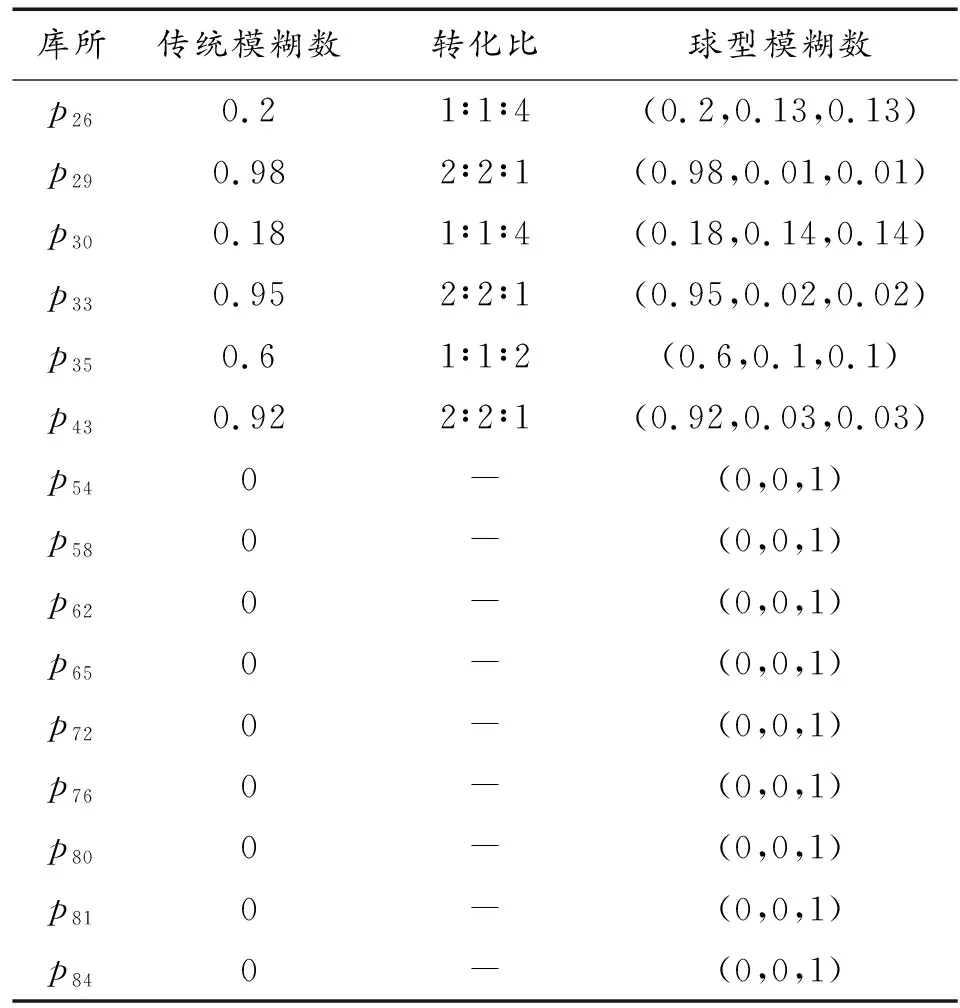
續(xù)表(表7)

2) 變遷信度值

變遷模糊數(shù)的轉(zhuǎn)化同樣遵循表4的轉(zhuǎn)化規(guī)則，球形模糊數(shù)取值如表8所示。

表8 變遷、變遷閾值Table 8 Transition threshold value table

3) 變遷閾值信度值

根據(jù)故障模式危害分類，得到了各故障模式的嚴(yán)重度評級及其球型模糊數(shù)取值，如表9所示。

表9 變遷閾值Table 9 Transition threshold value table

4.2 模型求解

車門開門故障Petri網(wǎng)模型中，有23個庫所，22個變遷，由此可以得到輸入矩陣、輸出矩陣如下：

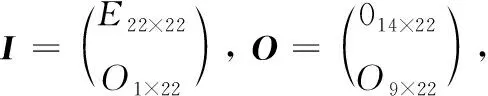
其中，

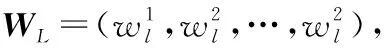
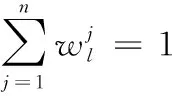
(9)

(10)

根據(jù)式(2)計算庫所最初始狀態(tài)

=(1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,0,0,0,0,0,0,0,0)

庫所含有一個Token，即故障模式發(fā)生，狀態(tài)為“1”，反之則為“0”,根據(jù)式(5)(6)計算輸入庫所信度值：

[(093,010,010),(029,013,013),

(086,004,004),(017,014,051),

(042,013,013),(065,008,008),

(086,004,004),(087,004,004),

(019,013,013),(087,004,004),

(015,015,015),(087,004,004),

(042,013,013),(086,004,004),

(0,0,1),(0,0,1),(0,0,1),(0,0,1),

(0,0,1),(0,0,1),(0,0,1),(0,0,1),(0,0,1)]

計算輸出庫所信度值

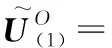
[(09,00,006),(00,00,10),

(042,01,017),(08,00,009),

(07,00,014),(039,001,018),

(084,00,007),(085,00,009),

(082,00,008),(00,00,10),

(081,00,008),(042,00,017),

(09,00,006),(031,00,016),

(00,00,10),(00,00,10),

(00,00,10),(00,00,10),

(00,00,10),(00,00,10),

(00,00,10),(00,00,10)]

根據(jù)式(1)～式(8)的方法計算出最終信度值，將其與TFPN模型結(jié)果一起列表，如表10所示。

表10 模型故障模式信度值推理結(jié)果Table 10 Comparison of inference results of reliability values of failure modes

將TFPN模型與SFPN模型信度值作圖，如圖14所示。由圖可知，兩者信度值趨勢大致相同，證明SFPN模型法具有可靠性。

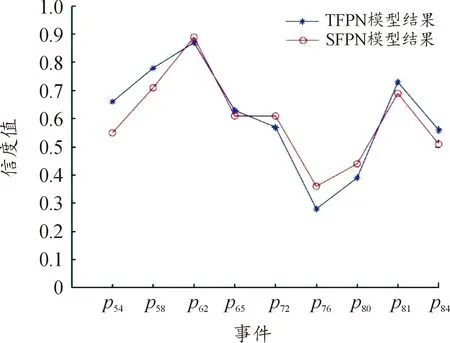
圖14 2種模型信度值曲線Fig.14 Comparison of reliability values between two models

根據(jù)文獻(xiàn)[16]中對球型模糊元中對球型模糊集的比較方法，可結(jié)合球型模糊值中的中立度、非隸屬度數(shù)值對故障事件信度值嚴(yán)重程度進(jìn)行進(jìn)一步判斷。

根據(jù)式(11)計算故障事件信度值的得分函數(shù)，再根據(jù)式(12)進(jìn)行2個故障事件嚴(yán)重度的判斷。

(11)

式(11)中，[0,q]為信度值取值范圍，故此處取q=1。s、d為球型信度值中的隸屬度、非隸屬度。

()>(), 則>

()<(), 則<

(12)

當(dāng)S(T)=S(T)時，需要根據(jù)式(13)進(jìn)一步計算精度函數(shù)，并根據(jù)式(14)進(jìn)行嚴(yán)重度判斷。

(13)

式(13)中，s、i、d為隸屬度、中立度、非隸屬度。

()=()且()>(),則>;

()=()且()<(),則<;

()=()且()=(),則=;

(14)

以解鎖失效導(dǎo)致的車門開門故障為例，推演其故障傳播路徑，如表11所示。

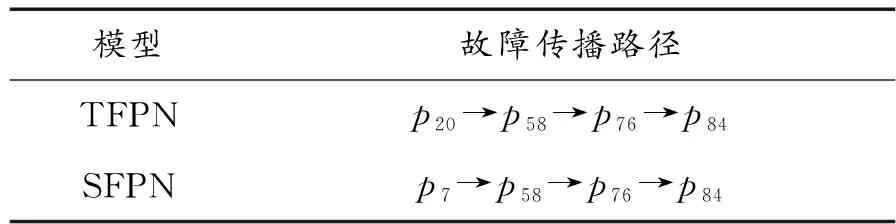
表11 故障傳播路徑Table 11 Comparison of fault propagation paths

TFPN模型中推理的故障傳播路徑源頭為“解鎖撞塊斷裂”，如表7所示，初始模糊信度值為(0.92,0.03,0.03)；SFPN模型給出的傳播路徑源頭為“插拔干涉”，初始模糊信度值為(0.97,0.01,0.01)。

根據(jù)球型信度值中的隸屬度，隸屬度為097，隸屬度為092，初步判斷嚴(yán)重程度>。

根據(jù)式(11)計算得到和的得分函數(shù)分別為139和136，因此進(jìn)一步判斷嚴(yán)重程度>。由于二者得分函數(shù)不同，不需要進(jìn)一步計算精度函數(shù)。

因此可以判斷：最可能因解鎖裝置故障而導(dǎo)致車門開門故障的傳播路徑應(yīng)為→→→。

由此可以得出結(jié)論，結(jié)合SFPN模型法中補(bǔ)充的中立度、非隸屬度2個判斷標(biāo)準(zhǔn)，該方法能比傳統(tǒng)模型法更全面、準(zhǔn)確描述故障模式。

5 結(jié)論

所使用的基于球型模糊Petri網(wǎng)模型(SFPN)的車門故障診斷方法，在保證可靠性的同時，提升了準(zhǔn)確性。SFPN模型法可以給出更準(zhǔn)確的故障傳播路徑，適用于復(fù)雜地鐵的故障診斷。故障發(fā)生時，檢修人員可以根據(jù)該模型給出的推理路徑進(jìn)行逆向檢索，快速確定故障發(fā)生源，有效提升檢修工作效率。