品數學文化 探微課教學
——以“趙爽弦圖”為例

黃麗娟

(福建省莆田市城廂區霞林學校，福建 莆田 351100)

一、背景介紹

“趙爽弦圖”被譽為中國數學界的圖騰，2002年在北京召開的國際數學家大會上，就以此為會徽，足以見得它的完美趙爽是三國時期非常有名的數學家，他大約在222年的時候深入研究了《周髀算經》，書中的一段530余字的“勾股圓方圖”(后稱“趙爽弦圖”，其簡圖如圖1)注文是數學史上極有價值的文獻，這個注文也讓趙爽對勾股定理產生新的證明方法

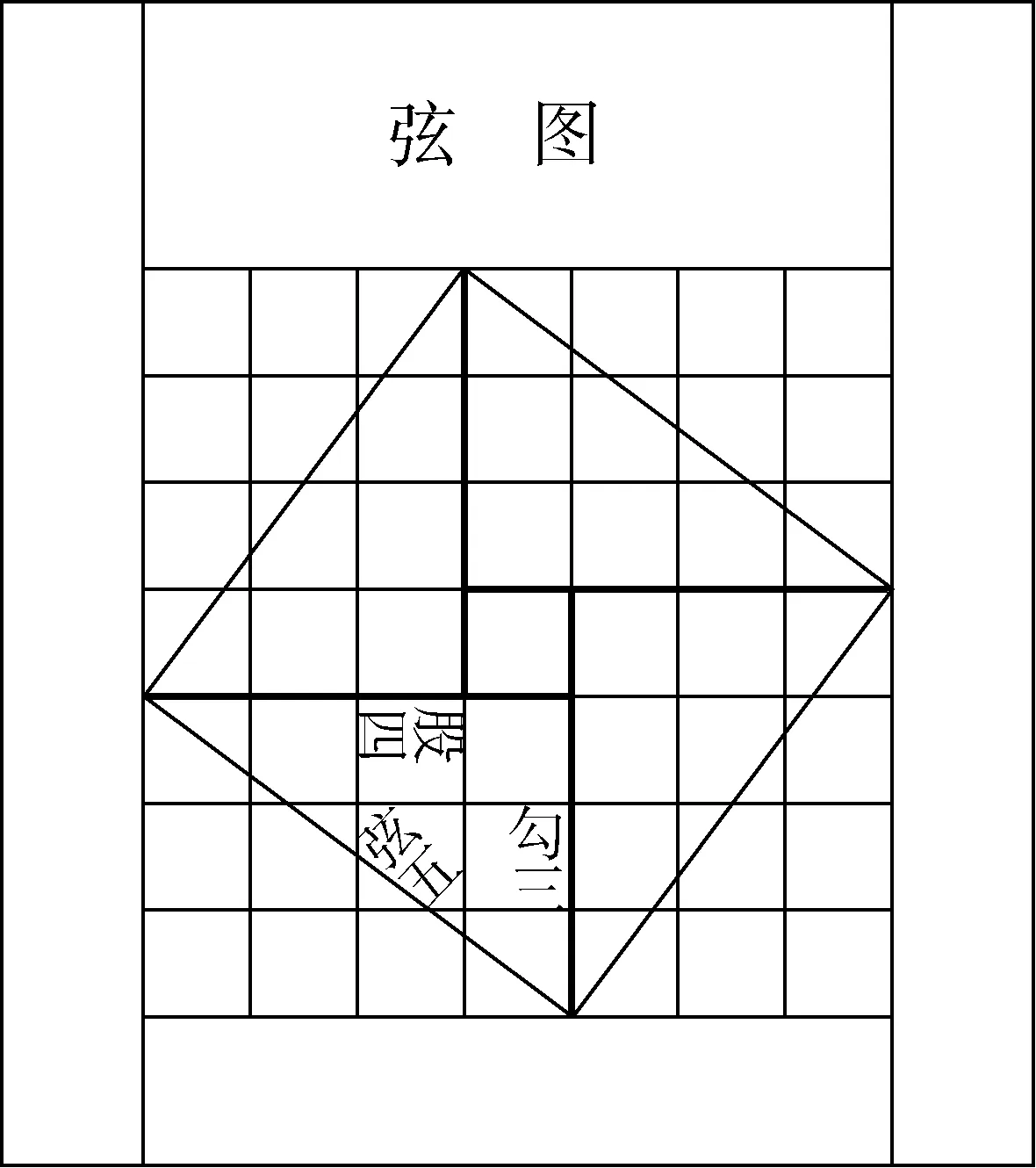
圖1

這個新的證明方法是這樣表述的：弦圖(如圖1)，又可以勾、股相乘為朱實二，倍之為朱實四；以勾、股之差自相乘為中黃實；加差實，亦成弦實趙爽的這個證明可謂別具匠心，他通過幾何的拼、補、割，證明代數之間的恒等關系，既具嚴密性又具直觀性，為中國古代以形證數、形數統一，讓代數和幾何緊密結合樹立了一個典范

二、中考鏈接

近年來，中考與“趙爽弦圖”有著千絲萬縷的聯系，各地市的考試也都能找到“趙爽弦圖”的影子

【典型例題A層】

(2018·莆田)如圖2，四個全等的直角三角形圍成一個大正方形，中間陰影部分是一個小正方形，這樣就組成一個“趙爽弦圖”，若=5，=4，則正方形的面積為________

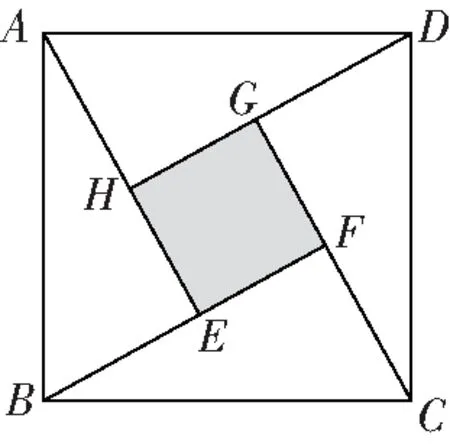
圖2

小結：(如圖3)

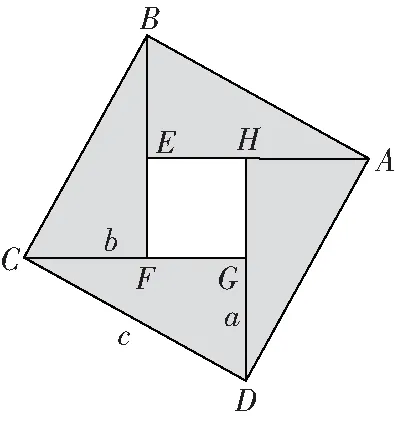
圖3

勾股定理：=+,=-,

正方形==+,

正方形=(-)，

4△=正方形-正方形=-(-)=+-(-)=2

【A層變式】

1(2020·寧夏)2002年8月，在北京召開的國際數學家大會會標取材于我國古代數學家趙爽的《勾股圓方圖》(如圖4所示)，其中大正方形的面積是15，小正方形的面積是3，直角三角形的較短直角邊長為，較長直角邊長為如果將四個全等的直角三角形按如圖5所示的形式擺放，那么圖5中最大正方形的面積為________

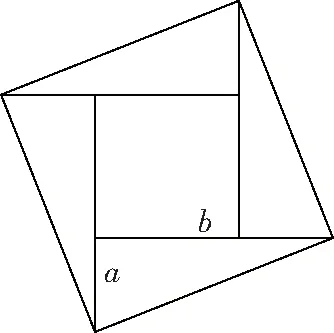
圖4

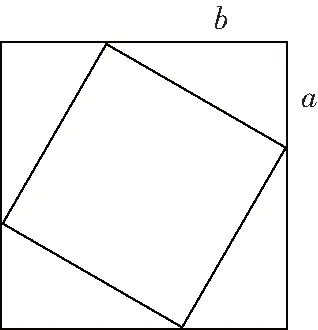
圖5

2如圖6所示，2002年8月在北京召開的國際數學家大會會標如圖所示，它是由4個直角三角形與中間的小正方形拼成的一個大正方形，若直角三角形最小的銳角為，大正方形的面積為25，小正方形的面積為1，則cos=________

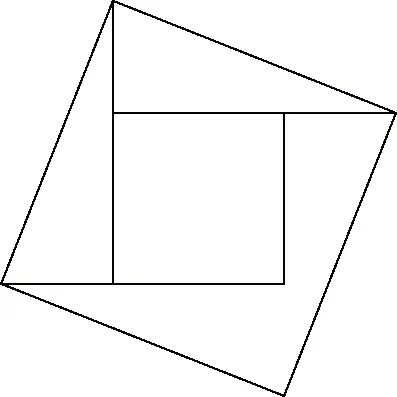
圖6

小結：變式的兩道題都可以通過前面的小結進行解題，在講解這兩道題時可以從兩個不同角度進行引導，其中第1題從已知條件出發，第2題則是從問題出發，讓學生體驗“逆向思維”的美妙

【典型例題B層】

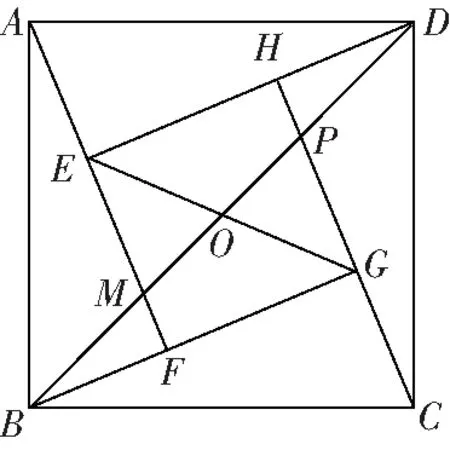
圖7

思路分析：

本道例題可以一題多解，結合本題的題型特征，方法一，可以采用選擇題中較為常用的賦值法，如設題目中涉及的線段為單位“1”，再結合相似求出它們的面積比；方法二，結合弦圖模型面積相等的關系，再結合三角形相似求得面積之比；方法三，可以直接通過正方形的性質，全等三角形等幾何圖形的相關知識，求出面積比

【典型例題C層】

如圖8所示，正方形的邊長為10，==8,==6,連接,則線段的長為________

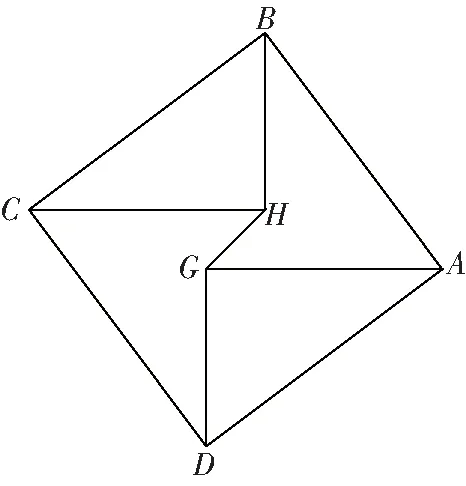
圖8

【C層變式】

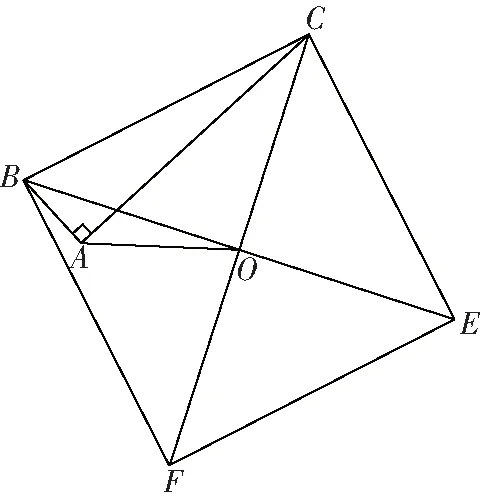
圖9

小結：在解決正方形問題時，分析已知條件，再結合“趙爽弦圖”的結構特征，通過補全“趙爽弦圖”進行解題，能夠為我們的解題帶來便捷

三、實踐思考

(一)尊重學生最近發展區，關注數學問題的變式

數學家哈爾莫斯說過，“問題是數學的心臟”在本微課中，教師結合學生接受問題的難易程度，設置了A，B，C三個層面的問題，這三層的問題由淺入深、層層遞進，設置問題時有意識地讓問題起點低，入口寬，同時在合適的時候對問題進行相應的變式，以求一題多變，提升學生的思維在設計本微課時，教師考慮到“趙爽弦圖”是在勾股定理的證明時引入的，由等積法作為鋪墊，學生在此前已有一定的邏輯基礎.因此，在尊重學生最近發展區的前提下，A層問題主要考查“趙爽弦圖”中的面積問題，在知識生成部分，教師可對例題進行適當的問題變式，幫助學生建立知識間的內在聯系，發散學生的思維，培養學生靈活多變的思維品質.最后的C層題目中是在原有例題的基礎上進行合理的變式，這樣處理的目的是打破學生思維的平衡，引起學生適當的焦慮，刺激學生努力去思考問題，如果學生有障礙，就有了繼續觀看下去的內驅力.

(二)構建邏輯連貫，走出思維迷宮

著名數學家龐加萊這樣說道：“邏輯用于證明，直覺用于發明”趙爽為了證明勾股定理，進行了一系列的變換他的證明之巧，心思之細膩無與倫比本微課在勾股定理的論證方面不予累贅，在微課中通過一系列的習題展示數學嚴謹的邏輯思維微課中三個層面的習題先由最簡單的直接套用公式，再到有弦圖的模型，結合相似等知識進行鞏固，最后撤掉弦圖的模型，需要自己添加輔助線構造模型，以此來達到由淺入深、深入淺出的效果在這幾個層面的習題設置時始終貫串“趙爽弦圖”這根主線

微課中的B層習題有意識地引入前年的一道中考真題，本道真題采用一題多解，目的就是培養學生思維的靈活性.本題乍看圖形不簡單，沒有已知相關的數據，后面要求的是兩個正方形的面積之比.同學們的常規思維會去求相應的邊長，再結合面積公式求解，朝著這個方向走下去會走進“思維迷宮”.為了有效避免這種情況，微課中結合題型特征，以及前面“趙爽弦圖”圖形結構特征的鋪墊，講解時先由學生慣性思維“想知道邊長又不懂得”，借勢引入了賦值法，再結合三角形相似求出相應邊長間的比例，最后結合“趙爽弦圖”中面積的特征順利解出二者的面積之比.

C層的例題是在前面兩個層面例題的基礎上在思維層面有所提升.在解決部分正方形問題時，學生需要在深刻理解“趙爽弦圖”的模型下，利用“趙爽弦圖”結構本身的特殊性，通過補全弦圖進行解答，從而使問題得以快速解決.當然，在錄制完本微課時，筆者自認為在講解C層例題時思維的引導還是不夠，對于怎樣想到添加輔助線，構造“趙爽弦圖”解題，為什么要這么操作的講解還是不夠細致，若在這方面思維引導得更加到位，效果應該會更好.

(三)微課教學與數學文化齊飛

數學，顯性的是知識、模型和邏輯，隱性的是思想與方法，其背后蘊含的是豐富多彩的數學文化本微課最大的亮點是對數學文化的滲透，開始時教師先介紹高考考試大綱對數學文化的重視，由此讓學生對考綱有了進一步的認識同時，為了讓學生深入理解數學文化的內涵，引領學生走上數學大道，微課中詳細介紹了趙爽相關信息正如張奠宙先生所說過的，“當我們真正地把數學文化的魅力滲入教材、到達課堂、融入教學時，數學就會更加平易近人，讓大家通過文化層面易于理解數學、喜歡數學、熱愛數學”美中不足的是本微課除了直觀呈現“趙爽弦圖”之外，在現代信息技術方面的應用應該繼續深挖

四、結束語

“趙爽弦圖”作為中國數學界的圖騰，經典且久遠本節微課通過一題多變，一題多解，結合數形結合思想、方程思想、從特殊到一般等常見的數學思想，感受到邏輯思維、圖形幾何直觀、數學運算等數學核心素養這些都是課程改革中強調需要具備的素養，因此，我們要好好欣賞“趙爽弦圖”，提升數學文化底蘊