《線性代數》學習中三次方程求根方法探討

萬前紅

(湖南工商大學理學院，湖南 長沙 410205)

《線性代數》是高等學校理科、工科及經濟類等非數學專業本科生必須學習的一門公共基礎課程，該課程具有概念多、抽象、邏輯嚴密等特點線性代數知識體系中，包含兩個重要內容，一個是線性方程組解的判別，另一個是方陣特征值的計算眾所周知，《線性代數》是以線性方程組為主線發展起來的，從而線性方程組解的判別與求解對于學習線性代數十分重要方陣特征值與特征向量是計算方陣高次冪、二次型化標準型的重要方法的基礎

若一個實際問題轉化成系數矩陣為方陣且含有參數的線性方程組，我們需要對其解進行判別，如例1

針對例1，我們可以使用初等變換法將系數矩陣化為行階梯形或行最簡形，然后利用系數矩陣的秩與增廣矩陣的秩以及它們與未知數之間的關系來判別方程組的解但系數矩陣含有參數，不僅在化行階梯形或行最簡形的過程中容易出錯，而且討論含參數的系數矩陣與增廣矩陣的秩以及它們與未知數之間的關系來判別方程組解的難度也不小又因為系數矩陣是方陣，所以我們可以考慮使用克萊姆法則來進行判定

對含有個未知量、個方程的線性方程組

(1)

注：在克萊姆法則中，系數行列式=||不等于零，是方程組(1)有唯一解的充分必要條件

根據克萊姆法則，我們來解例1：

利用集合補集的計算，我們有：方程組無解或有無窮多解當且僅當=≠0或者=0

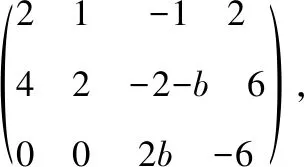
在解答例1的過程中，我們發現最關鍵的一步是計算系數矩陣的行列式不等于零，而此過程相當于計算一個三次方程根的補集

若要計算一個方陣的特征值，如例2

由線性代數知識可知，方陣的特征值是其特征多項式的根針對例2，即是求

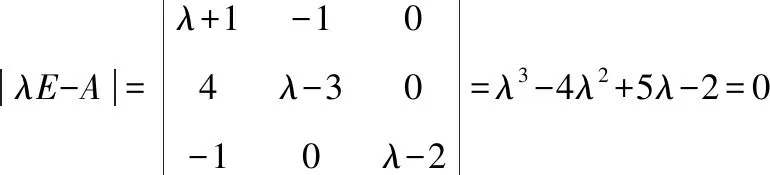
的根

由此我們發現解決例1、例2均以求方程的根為基礎很多學生對解決例1和例2的方法步驟是比較清晰的，但是卻沒有得到最后結果經過調查分析我們發現，主要問題在于學生不會計算高次方程的根下文就方程求根問題，結合線性代數知識列舉幾種方程求根方法

1 整系數多項式的有理根

該引理提供了一個求整系數多項式全部有理根的方法見下例3

為了更好地利用引理1求方程的有理根，我們需要下面引理：

設是次多項式方程()=0的重根的充分必要條件是()的階導函數()()=0(=0,…,-1)，且()的階導函數()()≠0

3求例2中方程-4+5-2=0的所有根

令()=-4+5-2,次數最高項的系數為1，因而因子為±1；常數項為-2，因而因子為±1,±2由引理1，方程的所有有理根可能為±1,±2經驗證，2和1為方程的根

()的導函數′()=3-8+5經驗證，1為′()的根,2不是″()的根,由引理2可知，1為()的二重根因此我們找到了()的三個根：2，1，1由代數學基本定理可知(參見[1])，三次方程共有3個根，因此我們找到了()的所有根

需要說明的是，該引理中雖然要求多項式的系數為整數，但是對一般的方程，我們可以通過系數處理，使其變為整系數

2 利用行列式的性質尋找根

如果行列式中兩行(列)元素對應成比例，那么行列式值為零

我們用一個例子來說明如何利用該性質求方程的根

矩陣的特征方程為

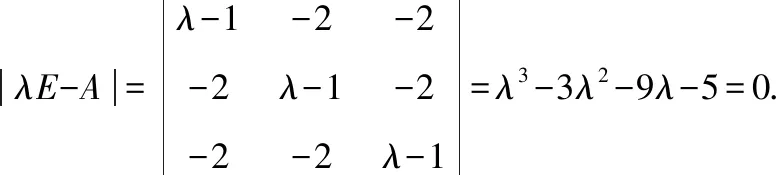
若

則行列式的第1行和第2行元素對應成比例，由性質1可知，此時-1=-2滿足方程，即=-1是方程的根所以

|-|=-3-9-5=(+1)(),

其中()可按多項式的除法得到具體計算如下：

即()=-4-5所以|-|=(+1)(-4-5)=(+1)(-5)從而，方陣的特征值為=5，==-1

若行列式中有一行(列)元素全為0，則行列式的值為0

我們以例2為例說明該性質的應用

此題還可以按下面性質來考慮：

行列式的值等于其某一行(列)的元素與其對應的代數余子式乘積的和

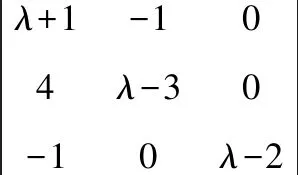
從而矩陣的特征值為2，1(二重)

性質3提示我們，在處理高階行列式時，我們可利用行列式的初等變換，將行列式的某行(列)化成只有一個元素不為零然后利用性質3，即可分離出特征多項式的一個因式，從而找到特征多項式的一個根且可以一直重復此步驟，直到將行列式的階數降為2階為止

3 直接利用三次方程的通用求根公式

3.1 將一般三次方程轉化為不完全三次方程

3.2 不完全三次方程求根

其中是虛數單位該方法的最大優勢是可以找出三次方程無理根和復數根三次方程的根還有其余表示形式，參見[4]

5求+1=0的全部根

利用因式分解+1=(+1)(-+1)及二次方程的求根公式，很容易驗證上面用不完全三次方程求根公式法計算出來的根是正確的

4 結 語

線性方程組在現實生活中的應用是非常廣泛的,不僅可以廣泛地應用于數學自身，還可以應用于經濟學、統計學、工程學、計算機科學、物理學、力學、通信、航空等學科和領域，相關問題均可將問題轉化為線性方程組求解特征值與特征多項式也廣泛地應用于數學自身，如，Fibonacci數列通項公式計算、矩陣高次冪的運算、二次型的標準化等，同時也應用于其他領域，如統計學中的主成分分析法本文所介紹的三次方程求根方法為線性方程組解的判別、特征值的計算提供了更多途徑，幾種方法之間可以融合起來使用，且均可以應用到高次方程的求解，為我們奠定學習線性代數的基礎