窄帶型Eu2+摻雜熒光粉理論研究進展

朱坤領，游歡歡，高發明，賈永超

（燕山大學 環境與化學工程學院，河北 秦皇島 066000）

1 引 言

發光二極管（LED）照明具有壽命超長、高效節能、全固態照明、抗惡劣環境、響應快、工作電壓低、抗震性及安全性好等諸多優點，被公認為21世紀最有潛力替代傳統照明器具的新光源。近幾年來，LED作為下一代新型照明光源逐漸進入如汽車、LCD背光源、室內、室外照明等廣泛的行業中，LED應用正在變得更加普遍。目前，白光LED的實現主要基于InGaN藍光LED芯片和具有石榴石結構的Y3Al5O12∶Ce3+（YAG∶Ce3+）黃色熒光粉組合方法得到，即熒光粉吸收一部分來自于LED芯片的藍光轉化為黃光，進而通過顏色互補原理實現白光器件[1]。該白光實現方法簡單有效，在工業界被廣泛使用。但其亦存在YAG∶Ce3+發射光譜中紅色成分不足的問題，導致難以獲得高顯色指數的暖白光器件[2]。因此，為提升白光LED在顯色指數方面的性能，亟需研發得到可藍光激發的高效紅光材料。Eu2+離子憑借獨特的4f-5d光譜躍遷特性，其相應的發光材料引起了廣泛關注。

在以上背景下，世界照明協會與美國能源部對白光LED燈用Eu2+基紅色熒光材料做出以下性能參數要求[3]：（1）紅色熒光粉的發射位置要位于610 nm左右；（2）在LED工作溫度450 K條件下，紅色熒光粉的熱猝滅應低于5%；（3）紅色熒光粉的發射峰寬要小于30 nm。對于上述性能參數（1）和（2）的要求，已有相對應的理論模型進行指導分析。例如，代爾夫特理工大學Dorenbos教授在近20年的工作基礎上[4-6]，獲得了一系列定量擬合公式來進行熒光粉發射位置和熱猝滅性質的計算，獲得了與實驗值非常匹配的結果。總而言之，對Eu2+離子在晶體中的發射位置和熱猝滅兩個方面的發光行為，人們已經有了從原子尺度上的認識，這些認識可以精確地指導實驗。

然而，在性能參數（3）方面的研究現狀卻表現得非常不理想。事實上，我們缺乏對Eu2+離子激活發光材料發射峰寬從微觀尺度的理解。為得到窄帶型Eu2+離子激活發光材料，目前的研究工作主要基于實驗經驗。例如，近期德國慕尼黑大學Schnick教授、華南理工大學夏志國教授、因斯布魯克大學Huppertz教授成功合成了一系列窄峰寬的Eu2+激活發光材料[7-13]，在很大程度上彌補了稀土發光領域在峰寬研究方面的不足，進而獲得了廣色域的顯示器件。盡管如此，已有的實驗工作仍然缺乏對晶體中Eu2+離子的發光材料發射峰寬從原子尺度的理解。因此，為實現參數（3）的性能要求，亟需進行更深入的理論研究工作，進而為窄帶型Eu2+離子激活發光材料的設計提供指導。

針對以上問題，本文擬從位形坐標模型出發，討論結構弛豫、斯托克斯位移、聲子頻率等因素對固體中Eu2+離子發射半峰寬（FWHM）的影響，并結合局部配位環境、激發態電子云分布等信息，綜述Eu2+摻雜窄帶發射熒光粉的形成原因，嘗試為發展新型Eu2+窄帶發射熒光粉提出理論依據。

2 發射峰寬計算的理論基礎

與原子躍遷的線狀光譜不同，Eu2+離子的4f-5d光譜躍遷在晶體中表現出帶狀發射。該發射帶由零聲子線（Zero-phonon line）和聲子伴帶（Phonon sidebands）構成。零聲子線和聲子伴帶則可以依據位形坐標模型進行計算分析。因此，為理解發射光譜峰寬的影響因素，應該清楚位形坐標模型（Configuration coordinate diagram，CCD）的具體含義。位形坐標模型的發展源自于康登對雙原子分子的研究[14-15]，該模型依賴于基態和激發態的平衡核構型的線性組合，后被廣泛地應用于分析分子和摻雜固體中的光致發光，開拓了發光定性分析的領域。

圖1為Eu2+摻雜熒光粉的4f-5d躍遷的一維位形坐標模型示意圖[16-17]。圖中下方的4f曲線表示Eu2+最外層電子構型為4f7的勢能線，而5d曲線表示Eu2+最外層電子構型為4f65d激發態的勢能線。激發和發射過程為：在外來光子的激發下，處于4f的電子吸收光子帶來的能量（Eabs）發生躍遷，至5d能級（A0→A*0），從而得到激發態Eu2+。此時穩定的基態結構平衡（Qg）被打破，原子位置將發生弛豫過程（A*0→A*）。結構弛豫后，整個系統將達到一個新的平衡態（Qe），然后電子從5d能級躍遷回4f能級并放出光子（A*→A）。最后體系再次通過多聲子弛豫過程使結構回到基態（A→A0）。基于這一模型便可以對Eu2+離子激活熒光粉發射半峰寬進行預測。

圖1 Eu2+離子摻雜熒光粉的一維位形坐標模型Fig.1 Configuration coordinate diagram of Eu2+-doped phosphors

勢能曲線表示能量與位形坐標Q之間的依賴關系。在單一聲子頻率以及簡諧近似條件下，基態和激發態的勢能曲線分別可以表示為：

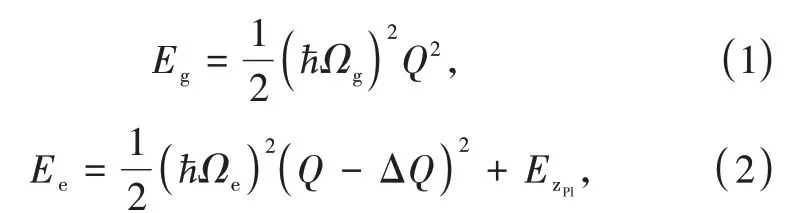
其中，EzPl為零聲子線的能量，ΔQ代表從基態到激發態下的晶體結構弛豫值，Ωg和Ωe分別是基態和激發態曲線中與4f-5d躍遷耦合的的聲子頻率，?為狄拉克常數。

Eu2+離子4f-5d光譜躍遷過程所吸收和發射的能量分布為Eabs和Eem。另外，在光吸收過程中電子-聲子耦合導致了能量損失，定義為Franck-Condon位移，用EFc,e來表示，類似地，EFc,g表示在光發射過程中晶格損失的能量[18]。依據EFc,g和EFc,e可以對Ωg和Ωe值進行如下計算[16]：

為描述電子-聲子耦合的強度，可以引入黃-里斯因子S，即結構弛豫過程中釋放聲子的數目。激發和發射過程的S因子分別用Sabs和Sem來表示，可以依據公式（5）～（6）進行計算：

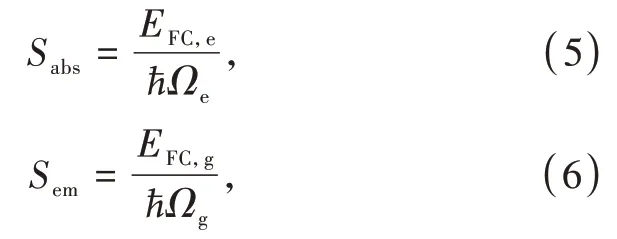
依據以上計算得到的信息，表征發射峰寬的物理量半峰寬（Full-width at half-maximum,W）在0 K條件下可以表示為[16]：

進而，在任意溫度T（K）條件下，發射半峰寬的值為：

通過上述計算公式，可以看到影響半峰寬的本質參數為晶體結構弛豫和有效聲子頻率以及所對應的斯托克斯位移和黃-里斯因子的大小。以下將分別對這些參數進行討論。

3 Eu2+離子光譜躍遷中的結構弛豫

固體熒光粉在吸收一定能量的光子后，受激輻射出能量小于原吸收的光子，從而導致發射光譜相較于激發光譜向能量較低的方向偏移。這一過程是由于晶體結構弛豫所造成的，進而使兩個光子的能量存在差值，即為斯托克斯位移。對于Eu2+激活發光材料的斯托克斯位移，劉泉林教授課題組等對其影響因素進行了總結分析，并提出斯托克斯位移與Eu2+離子局部配位環境平均鍵長表現出正相關性[19]。本小節著重討論斯托克斯位移對發射半峰寬的影響。該影響可以通過固定聲子頻率的位形模型進行直觀的表現，如圖2所示。由此可以看出，Eu2+離子4f-5d光譜躍遷中結構弛豫越小，所得到發光材料會具有越窄的發射峰寬。因此，如何獲得具有較小結構弛豫的Eu2+摻雜熒光材料成為關鍵。下文分別從配位環境和結構剛性角度對以往研究進行說明。

圖2 結構弛豫對Eu2+摻雜熒光粉發射峰寬的影響Fig.2 Schematic representation of the effect of geometry relaxation on FWHM of Eu2+-doped phosphors

3.1 配位環境

通過以往的研究可知，Eu2+激活發光材料實現窄帶發射通常需要化合物具有單一的摻雜位點以減少多發射中心造成光譜重疊，進而造成發射光譜出現展寬。與此同時，在窄峰寬發光材料的設計中，高對稱性的配位環境被認為是制備窄帶發射熒光粉的關鍵因素之一。常見的高對稱性配位Eu2+離子摻雜窄帶發射LED燈用熒光粉有以下三種典型種類，圖3列舉了其代表性化合物的晶體結構以及Eu2+離子摻雜的局部配位環境。

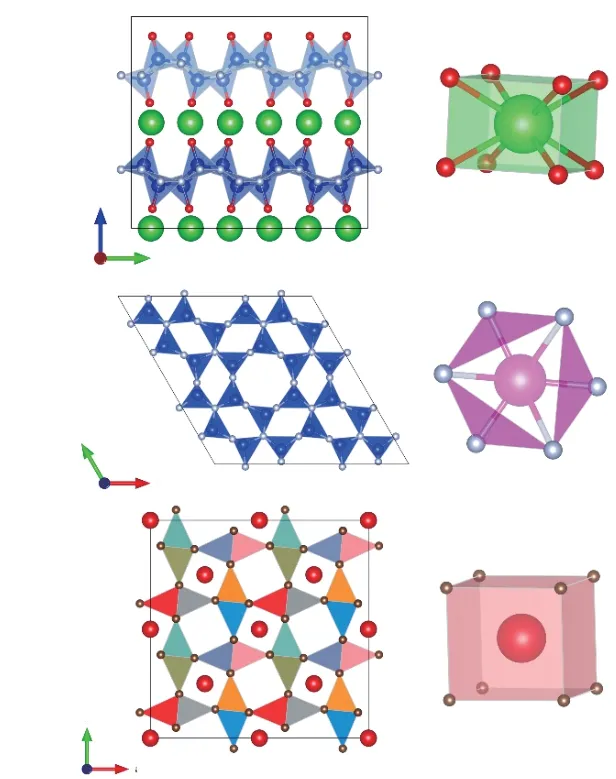
圖3 三類Eu2+摻雜窄帶發射熒光粉晶體結構及其對應的局部配位環境Fig.3 Three representative crystal structures and local coordination environments of Eu2+-doped narrow-band emitting phosphors

第Ⅰ類是BaSi2O2N2型結構。這類熒光粉晶體結構屬于正交Pbcn空間群，陰離子形成高度凝聚的SiON3四面體，Ba2+離子作為電荷補償劑填充到孔道之中，以類立方配位的環境存在。Eu2+離子占據到Ba2+的晶體格位。在405 nm的近紫外激發條件下，Eu2+離子的發射光譜的峰值和FWHM分別為494 nm和968 cm-1[20]，表現出青光窄帶發射特點。

第Ⅱ類為β-SiAlON型結構。該類窄帶發射熒光粉晶體結構屬于六方P63空間群，其化學式為β-Si6-zAlzOzN8-z（0＜z≤4.2）[21]。β-SiAlON型結構由共享的（Si，Al）-（O，N）4四面體和沿[001]方向六邊形通道所組成。與第一類熒光粉明顯不同的是，Eu2+活化劑并不是取代已有原子的格位，而是占據其六邊形孔道的空位中，Kimoto等已直接通過掃描透射電子顯微鏡觀察到[22]，隨后Wang等也通過理論計算進一步證明[23]。六邊形空位的占據使得其結構不會因Eu2+的引入而發生劇烈畸變，同時在激發和發射的弛豫過程中結構也會保持較高的穩定性，最終表現為較大剛性的窄帶發射。同時，在β-SiAlON型結構中，z值的大小會導致發光特性不同，如在相同激發光源下（325 nm），高z（0.18）-β-SiAlON發射峰位置 和FWHM分 別 為540 nm和1 870 cm-1，而 低z（0.03）-β-SiAlON發 射 峰 位 置 和FWHM分 別 為528 nm和1 772 cm-1[21]。盡管z值不同會導致其發光性質改變，但仍可以看出不同z值下發射光譜均表現出窄帶發射特性。

第Ⅲ類為UCr4C4型結構。近期報道的UCr4C4化物包括Schnick教授課題組開發的Eu摻雜SrLiAl3N4（SLA）、SrMg2Al2N4（SMA）、SrMg3SiN4（SMS）等一系列熒光粉。其中，SLA屬于三斜晶系P1空間群，Li+和Al3+與陰離子組成[LiN4]、[AlN4]四面體構成剛性通道。SLA∶Eu2+為紅色窄帶發射光譜，在440 nm的激發波長下，峰值和FWHM分 別 為650 nm和1 180 cm-1[7]。SLA∶Eu2+還表現出較為優秀的熱穩定性質，與室溫相比，其在500 K時的發光強度僅降低了約5%，由此它被認定為下一代紅色熒光粉的候選者。SMA屬于四方晶系I4/m空間群，Mg2+和Al3+與陰離子組成[MgN4]、[AlN4]四面體構成剛性通道。與SLA相比其構成通道四面體表現出更大的無序性，這也使得結構的剛性有所減弱，從而進一步導致其發射光譜出現一定程度的展寬。SMA∶Eu2+同樣為紅色窄帶發射光譜，在440 nm的激發波長下，峰值和FWHM分別為610 nm和1 838 cm-1[24]，略寬于SLA∶Eu2+。SMS屬于四方晶系I41/a空間群，與前兩者相似，Mg2+和Si4+與陰離子組成[MgN4]、[SiN4]四面體構成剛性通道。相較于前者，兩種配位四面體有序排列，使得其結構表現出較大的剛性。在450 nm的激發波長下，峰值和FWHM分別為615 nm和1 170 cm-1，發射半峰寬為三者之中最窄[25]。近期夏志國教授課題組報道了一些新型UCr4C4氧化物類型熒光粉，如RbLi（Li3SiO4）2（RLSO）和Na0.5K0.5Li3SiO4（NKLSO）等。其中RLSO晶體屬于C2/m（單斜晶系）空間群，在460 nm的激發光源下表現為綠色窄帶發射，其峰值和發射峰寬分別為530 nm和1 497 cm-1[26]。而NKLSO晶體則屬于I4/m（四方晶系），在400 nm的激發光源下，光譜由486 nm（FWHM約為847 cm-1）處的主要不對稱窄帶峰和530 nm處的從屬肩峰組成[27]，表現出青色發射。

表1中列舉了以上三類窄峰型Eu2+摻雜熒光粉的光譜信息和配位環境。圖4展示了上述三種典型的Eu2+摻雜窄帶發射熒光粉的激發和發射光譜。由上述分析可知，為實現Eu2+摻雜更窄的發射特性，通常對局部配位環境的對稱性有較高的要求。衡量局部配位環境的畸變程度可以通過以下公式來描述[28]：其中D是中心離子-陰離子配位多面體的畸變指數，li是中心原子到第i個配位原子的鍵長，lav則為配位多面體的平均鍵長。由以往的研究可知，較大的配位環境畸變往往導致4f-5d光譜躍遷中較大的晶體結構弛豫，進而展寬其發射光譜帶。而在UCr4C4[11]類型Eu2+激活熒光粉中，Eu2+離子占據U離子的晶體格位，局部配位環境由六面體構成。以SLA∶Eu2+為例，該熒光粉中Eu2+離子局部配位環境的畸變指數D近乎為0，保證了窄帶發射。

表1 三類Eu2+摻雜窄帶發射熒光粉的發光特性Tab.1 The luminescent properties of Eu2+-doped narrow-band emitting phosphors with three representative crystal structures

圖4 三類Eu2+摻雜窄帶發射熒光粉的激發和發射光譜Fig.4 The excitation and emission spectra of Eu2+-doped narrow-band emitting phosphors

3.2 結構剛性

通過上述近期研究較多的三類Eu2+激活窄帶發射熒光粉，不難看出高對稱性的晶體格位往往可以導致Eu2+離子的窄帶發射。但實際研究表明，在一些低對稱性的配位環境中，Eu2+離子也可以表現出窄帶型發射。該類材料以硼酸鹽居多，例如SrB4O7∶Eu2+[16]。對于該類型發光材料，其窄帶發射的解釋往往歸結到材料剛性，即材料晶體結構的高穩定性使得其在光譜躍遷中具有較小的弛豫，這就使得電子躍遷過程與周圍環境存在較少的能量傳遞，從而使其發射半峰寬具有較小值。化合物結構剛性可以通過計算材料的德拜溫度來判定：高德拜溫度對應高的結構剛性。因而德拜溫度為實現Eu2+摻雜窄帶熒光粉的篩選提供了依據[29]。德拜溫度（θD）的大小可采用如下公式進行計算：

其中Cp代表化合物的比熱容，N是每個分子式單元的原子數乘以阿伏伽德羅常數，kB是玻爾茲曼常數，T是溫度，θD則為該化合物的德拜溫度。以β-Sialon熒光粉體系為例，低z（0.03）-β-SiAlON和高z（0.18）-β-SiAlON材料所計算得到的θD分別為901 K和747 K，這表明低z（0.03）-β-SiAlON比高z（0.18）-β-SiAlON具有更高的熱穩定性，前者的結構剛性同樣高于后者，從而前者表現出更窄的發射半峰寬[21]。

4 聲子頻率的影響

4.1 基態與激發態聲子頻率做相等近似情況

在一般體系中，基態和激發態中有效聲子頻率Ωg和Ωe的值非常相近，通常僅存在～0.005 eV的能量差距，所以可以近似認為Ωg和Ωe相等。該近似處理可以對半峰寬計算公式（7）進行簡化。該情況下，從位形坐標模型可以看到激發和發射過程中的弗蘭克-康登能量位移相同，即EFc,e=EFc,g。這樣我們就可以把斯托克斯位移引入到計算公式之中。

根 據 斯 托 克 斯 位 移（ΔS）的 定 義，ΔS和Franck-Condon位移的關系如下：

從而對公式（7）進行整理，得到新的半峰寬計算公式[30]:

由上述公式可以清晰地看出，當斯托克斯位移相同時，高頻聲子模式會導致樣品的發射半峰寬值增大。這一分析可通過位形坐標進行表達，如圖5所示。具體而言，聲子頻率的大小將會對基態/激發態的勢能曲線形狀產生影響。由公式（1）～（2）可知，當聲子頻率增大，平衡位形拋物線開口將會變得更窄。因此我們便可通過不同聲子頻率下的一維構型坐標模型對發射半峰寬進行一定的分析。通過圖5可見，為獲得窄峰寬的Eu2+摻雜熒光材料，應盡量減小有效聲子頻率的值。在具體開發中，可以利用低頻局域聲子模式的概念進行材料的設計。

圖5 相同斯托克斯位移下，不同聲子頻率對半峰寬的影響。Fig.5 Schematic representation of the effect of effective phonon frequency on FWHM of Eu2+-doped phosphors

4.2 基態與激發態聲子頻率不相同情況

上述有效聲子頻率對FWHM影響的討論是以基態聲子頻率（Ωg）與激發態聲子頻率（Ωe）相等為基礎。在實際的設計中，可以進一步利用兩者的差異，進行窄峰型Eu2+激活熒光粉的開發。根據公式（3）～（4）可知，聲子頻率的大小將會直接影響Franck-Condon位移的大小。因此，可以引入一個新的參數來定義二者的差別，此處稱為ΔC[16,30]：上述公式和公式（11）聯立可得出新的Franck-Condon位移表述 形式[28]：

在LED工作溫度條件450 K下，玻色-愛因斯坦分布可以用玻爾茲曼分布代替。該條件下，FWHM與ΔC、ΔS以及溫度（T）的關系可以表示為[30]：

其中W(T)是LED工作溫度下的半峰寬值。

由公式（16）可知，在固定發射能量和斯托克斯位移下，激發和發射過程中Franck-Condon位移的差異是決定半高寬的關鍵因素。由于基態和激發態下的Franck-Condon位移均為正值，因此ΔCΔS的范圍處于-1～1之間[30]。在固定熒光粉ΔS及發射溫度T時，發射峰寬W(T)與ΔCΔS表現出負相關性，這一比值越大，半高寬越小。這就使得激發態和基態之間的正Franck-Condon位移差距有利于實現窄帶發射，如圖6所示。雖然該結論僅僅是基于簡單的單聲子位形模型來討論，其在考慮詳細振動模式頻率的情況下可能會有部分變化，但是在新型Eu2+摻雜熒光粉的高通量計算篩選時，ΔCΔS仍可以被認定為一個非常重要的參考量。

圖6 在ΔS和發射頻率固定的條件下，ΔC對半峰寬的影響。藍色曲線對應于ΔC為零，而紅色曲線對應于ΔC為正值。Fig.6 Schematic representation of excited state phonon frequency on FWHM of Eu2+-doped phosphors，with fixed Stokes shift and ground state phonon mode.The blue curve stands for a smaller excited state phonon frequency than ground state value，and the red lines stand for the opposite situation.

5 結 論

本文以位形坐標模型為理論依據，分析了Eu2+激活熒光粉的局部配位環境、結構剛性、聲子頻率等多個方面對其發射峰寬的影響，進而對實現窄帶發射的要點進行了歸納與總結，最終得到如下結論：（1）從結構方面，高剛性的晶體結構會使晶體弛豫程度減小，這就要求所選熒光粉基質材料晶體結構具有較高的結構剛性。（2）從配位環境方面，較大空間、較小畸變程度以及較大相鄰發射位點距離的高對稱性局部配位環境不僅能減小晶體的弛豫程度，還會使發射過程中能量重疊減小，進而減小光譜展寬效應。（3）從聲子頻率方面，在激發和發射過程中，耦合聲子頻率的大小對峰寬的影響也尤其重要，可以分為兩種情況：在基態與激發態聲子頻率近似相等時，較小的聲子頻率會引起更小的發射半峰寬；在二者不等時，激發態的高頻聲子耦合能夠導致窄峰寬。上述關于窄帶發射的各種因素可以為Eu2+摻雜窄帶發射熒光粉基質材料的篩選提供思路，有望作為描述因子來進行高通量計算篩選。

本文專家審稿意見及作者回復內容的下載地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220189.