Ce3+/Eu2+摻雜無機發光材料構效關系與唯象理論

王淑欣，宋 振，劉泉林

（北京科技大學 材料科學與工程學院，北京 100083）

1 引 言

Ce3+/Eu2+摻雜無機發光材料在照明、顯示、監測、示蹤、防偽以及信息存儲等領域具有重要應用。其中熒光粉轉換發光二極管（pc-LED）以其發光效率高、體積小、全固態以及耐久性好等優異性能廣泛應用于照明工業和液晶顯示背光源領域[1-4]。源于Ce3+/Eu2+離子的發光躍遷是宇稱允許的f-d電偶極躍遷，具有高效吸收和高效發射的優點；其激發能量取決于Ce3+/Eu2+激活劑離子的4f和5d能級之間的能量差。4f軌道的能級由于受到5s25p6殼層的屏蔽作用，其能量受外界環境的影響較小，基本不隨基質材料的改變而改變。與4f軌道不同，5d軌道處于外層，其能級能量受基質晶體結構和激活劑所處的局域結構的影響較大。共價鍵效應、晶體場劈裂和電聲子耦合作用可以有效調控其激發光譜和發射光譜，為基于組分-結構-性能的構效關系設計新型熒光粉提供理論依據和可行性[5-7]。另外，Ce3+/Eu2+摻雜LED熒光粉的發光性能還取決于其電子結構[8]，即稀土離子和基質材料的能級/能帶結構。

作為pc-LED實用的發光材料，應滿足以下要求：（1）具備和LED芯片發射光譜匹配的激發光譜；（2）合適的發射光譜；（3）高發光效率；（4）優異的發光熱穩定性；（5）優異的化學穩定性[9-10]。在過去幾十年中，研究人員成功研發出了一系列滿足以上要求的熒光粉，得到了覆蓋全部色調的商用白光發射LED器件。目前，商用LED熒光粉主要包括鋁酸鹽Y3（Al,Ga）5O12∶Ce3+、氮化物（Ca,Sr）-AlSiN3∶Eu2+、氧氮化物β-SiAlON∶Eu2+和（Ba,Sr）-Si2O2N2∶Eu2+、硅 酸 鹽（Ba,Sr）2SiO4∶Eu2+和（Ba,Sr）3SiO5∶Eu2+等[11-16]。本 文 系 統 介 紹 了Ce3+/Eu2+摻雜無機發光材料的構效關系與唯象理論的研究進展，詳細總結了基質材料組分、晶體結構、局域結構和電子結構對發光性能的影響規律。

2 Ce3+/Eu2+摻雜無機發光材料的構效關系與唯象理論

Ce3+/Eu2+摻雜無機發光材料的發光過程可以分為能量吸收、無輻射弛豫和輻射躍遷發光三個階段：（1）當受到激發時，激活劑離子Ce3+/Eu2+吸收能量使得電子從4f基態躍遷至5d激發態；（2）由于5d電子和晶格聲子發生耦合作用，部分激發能量以無輻射躍遷的形式散失，激發態弛豫到最低激發態；（3）弛豫后的5d激發態電子躍遷至4f基態發光[17]。因此，熒光粉的激發能量取決于Ce3+/Eu2+激活劑離子的4f和5d能級之間的能量差。基質對5d能級的影響通常可以使用質心移動εc和晶體場劈裂εcfs兩個參量進行表征，如圖1所示[18]。在基質材料中，由于共價鍵效應，電子間斥力減少，5d能級向低能方向移動；5個5d能級平均能量的下移稱為質心移動εc。此外，根據激活劑離子占據的晶體格位的對稱性，簡并的5d能級最多可分裂為5個不同的5d態；晶體場劈裂εcfs則為最高5d能級和最低5d能級之間的能量差。質心移動εc和晶體場劈裂εcfs的整體效應導致5d和4f能級之間的能量差減小，直接決定了材料的激發光譜所處的位置和帶寬。在已知激發譜的情況下，發射譜和峰位主要由電聲子耦合和斯托克斯位移ΔS決定。稀土離子的電子在從激發態回到基態發光之前，會與晶格聲子發生耦合使其部分激發能以非輻射躍遷形式散失，導致發射光相對于激發光紅移。這種相同電子態間電子躍遷的吸收和發射能量的差值稱為斯托克斯位移[19-20]。在過去幾十年中，研究者們研發出了許多Ce3+/Eu2+摻雜的無機發光材料，并深入理解其構效關系。在理論方面，Dorenbos建立了一套完整的唯象理論，為理解、預測、設計和調控稀土摻雜無機發光材料的性能提供了重要的科學依據[5]。本節綜述質心移動、晶體場劈裂、誘導效應、斯托克斯位移、發光效率和發光熱猝滅以及電子結構等相關研究進展，系統總結Ce3+/Eu2+摻雜無機發光材料的構效關系與唯象理論。

圖1 Ce3+/Eu2+發光性能與配位環境之間的關系[8］Fig.1 The correlations between the luminescence property of Ce3+/Eu2+and the coordination environment[8］

2.1 電子云擴展效應或共價鍵效應——質心移動

基質中Ce3+/Eu2+5d能級的平均能量（質心）低于自由離子中5d能級的平均能量，平均能量降低的大小稱為質心移動εc。質心移動通常被認為與電子云膨脹相關，稱為電子云擴展效應或共價鍵效應，與5d軌道和陰離子p軌道的共價性密切相關。共價性使鑭系陽離子的電子間平均距離增大，從而減少了庫倫斥力，產生質心移動[21]。1980年，Morrison首次提出配位極化模型，強調5d電子和陰離子配位電子的交互作用對質心移動的重要作用[22]。在配位極化模型中，金屬電子的瞬時位置使周圍配體極化，極化的配體又作用于金屬電子本身。這種自感電勢減少了金屬電子間的庫倫排斥，從而導致電子能量質心位置降低，即質心移動。

為了進一步定量地理解和預測化合物中摻雜稀土離子的5d能級的質心移動，在共價模型和配位極化模型的基礎上，Dorenbos提出一個新的參數，即光譜極化率αsp[23]。它綜合了（1）配體極化、（2）共價性和（3）電子云擴展效應對質心移動的影響。假設，（1）總質心移動是每個陰離子單獨貢獻的結果的疊加；（2）只有最近鄰陰離子對質心移動有顯著貢獻；（3）所有配體的極化率相同，則質心移動可表示為

其中Rj（pm）是在未弛豫晶格中Ce3+到陰離子j的距離；求和為N個近鄰配位陰離子配體的總和；ΔR≡RM-RLn，其中RM是被離子半徑為RLn的鑭系元素Ln取代的陽離子的離子半徑；0.6ΔR是鍵長弛豫的估計值。該關系式表征了代表發光性能的光譜極化率、代表化合物結構的離子間距和代表成分的電負性之間的關系。此外，Dorenbos建立了光譜極化率αsp和平均陽離子電負性χav之間的相關關系：

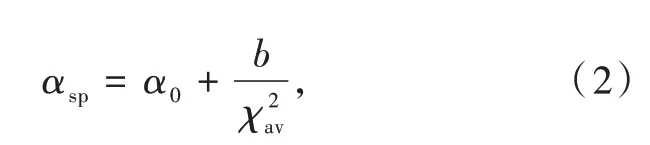
其中α0是極大χ情況下的極限極化率；b代表陰離子由于與金屬鍵合而改變其極化率的敏感性。平均陽離子電負性χav定義為

其中ni為化學式中帶有電荷zi和電負性χi的陽離子的數量。

基于以上理論，Dorenbos采用統計分析方法，通過分析Ce3+摻雜氧化物和氟化物的光譜和結構數據，得到了光譜極化率αsp和平均陽離子電負性χav之間的定量關系，如圖2（b）所示[24,26]。在氧化物中[23,26]：

圖2 （a）鹵化物和氧化物中Ce3+5d能級的質心移動[5］；（b）Ce3+摻雜氮化物、氧化物和氟化物中光譜極化率和平均陽離子電負性之間的相關關系[24］；（c）Ce3+摻雜氮化物熒光粉中光譜極化率αsp和平均陽離子電負性χav的相關關系的修正結果[25］。Fig.2（a）The centroid shift for Ce3+5d configuration in halides and oxide compounds[5］.（b）Spectroscopic polarizability against the inverse square of the average cation electronegativity in Ce3+doped nitrides，oxides，and fluorides[24］.（c）The revised correlation between the spectroscopic polarizability and the average cation electronegativity in Ce3+doped nitrides[25］.

近幾十年來，Ce3+/Eu2+摻雜氮化物發光材料由于其獨特的發光性能以及在白光LED領域廣泛的應用前景而備受關注。我們課題組研究了Ce3+摻雜氮化物中光譜極化率αsp和平均陽離子電負性χav之間的定量關系[24]。通過分析Ce3+摻雜氮化物的光譜和結構數據，得到了如圖2（b）所示的定量關系。對比氟化物和氧化物，我們得到bF＜bO＜bN，這是由于陰離子與金屬鍵合時電子云的極化程度按照由F到O到N的順序依次增加。這一結果說明通過O代替F或N代替O可以得到更大的質心移動，實現發光材料的光譜紅移。

熒光粉中Ce3+/Eu2+的配位結構對于研究其組分-結構-性能相關關系至關重要，然而很多化合物的配位結構數據在不同報道中相互矛盾。因此，我們課題組根據鍵價理論和配位多面體的穩定性提出了一套確定氮化物中陽離子配位數的統一標準[25]。在此基礎上，通過分析Ce3+摻雜氮化物發光材料的光譜數據和結構數據，修正了光譜極化率和平均陽離子電負性之間的定量關系如下（圖2（c））：

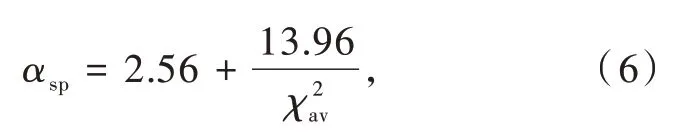
Dorenbos模型的建立為預測Ce3+/Eu2+摻雜無機發光材料的質心移動提供了理論依據，為基于材料組分和結構預測以及調控激發性能提供了參考和指導。

2.2 晶體場劈裂

Ce3+/Eu2+5d能級的晶體場劈裂εcfs拓寬了激發光譜，使Ce3+/Eu2+摻雜熒光粉可調控到被藍光等低能輻射激發。晶體場劈裂由5d電子和陰離子配體之間的交互作用、泡利作用以及庫倫作用共同引起。

Dorenbos通過分析六十多種Ce3+/Eu2+摻雜熒光粉（包括鹵化物、氧化物、硫化物和硒化物）的光譜和結構數據，揭示了晶體場劈裂和Ce3+/Eu2+周圍的配位環境之間的關系[27]。結果表明晶體場劈裂和激活劑離子的配位數、配位多面體的類型和尺寸密切相關，而與配位陰離子的種類無關。在Ce3+/Eu2+占據相同配位多面體的化合物中，晶體場劈裂可以表達為

其中βQpoly為常數，與配位體類型相關；Rav定義為

其中Ri是未弛豫晶格中鑭系離子到N個配位陰離子的鍵長；ΔR≡RM-RLn，其中RM是被離子半徑為RLn的鑭系元素Ln取代的陽離子的離子半徑；0.6ΔR是鍵長弛豫的估計值。通過分析擬合具有6配位八面體（Octa）、8配位六面體（Cubal）和12配位立方八面體（Cubo）的晶體結構的熒光粉的結構和光譜數據（圖3（a）～（c）），Dorenbos得到了具有不同配位環境的熒光粉的βpoly。不同配位環境中的Ce3+和Eu2+的βpoly值具有相同的比值，即βocta∶βcubal∶βcubo=1∶0.89∶0.44；對于12配位的Eu2+，βocta為1.36×105eV·pm2。此外，通過進一步分析擬合得到了Ce3+和Eu2+晶體場劈裂之間的關系[28]：

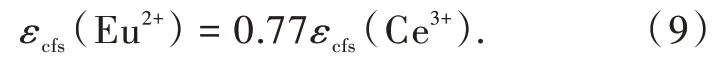
我們課題組進一步研究了Ce3+/Eu2+摻雜氮化物熒光粉中5d能級的晶體場劈裂與基質材料結構和組分之間的相關關系[6]。得到了晶體場劈裂與配位多面體的類型和尺寸的關系，如圖3（d）、（e）所示。結果表明晶體場劈裂隨著配位數的增加而減小。在配位數相同的情況下，晶體場劈裂εcfs與平均配位鍵長R-2av成正比。通過對比分析在相同氮化物中占據相同陽離子格位的Ce3+和Eu2+的晶體場劈裂數據，得到了線性相關關系

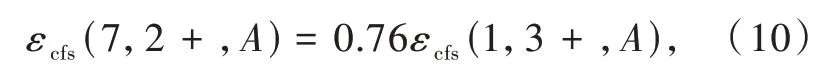
即在相同氮化物中占據相同陽離子格位的Eu2+的晶體場劈裂是Ce3+的0.76倍。Ce3+/Eu2+摻雜氮化物熒光粉的分析結果與Dorenbos在氟、氯、氧化物中得到的結論一致[28]，進一步證實晶體場劈裂主要取決于陽離子的配位多面體的類型和尺寸，與陰離子類型無關。晶體場劈裂與配位數密切相關，如圖3（d）、（e）所示，因此，可預測具有CaAl-SiN3結構類型的MgAlSiN3化合物可產生大的晶體場劈裂。據此，我們設計并制備出了CaAlSiN3∶Mn2+熒光粉。Mn2+在八面體六配位場下的基態與第一激發態的能級差與晶體場強度負相關，這一特性與Cr3+相反。然而，目前報道的Mn2+的發光在可見的綠光-紅光區。通過在Mg位置摻雜Mn2+，獲得了具有寬帶遠紅-近紅外發射的氮化物發光材料MgAlSiN3∶Mn2+。發射峰位于754 nm，半峰寬約150 nm。這為研發新型寬帶近紅外發光材料提供了一種策略[29]。

圖3 鹵化物、氧化物、硫化物和硒化物熒光粉中Ce3+（a）和Eu2+（b）5d能級的晶體場劈裂，以及其相關關系（c）[5，27-28］；Ce3+（d）和Eu2+（e）摻雜氮化物的晶體場劈裂ecfs；（f）Ce3+和Eu2+的配位環境。L為F-、S2-、N3-等配體，CN為配位數，Rradi為中心離子的離子半徑，RPCEM是配體和中心離子的平均距離，Reff是配體和中心離子的有效距離[6］。Fig.3 The crystal field splitting of the 5d configuration of Ce3+（a）[27］and Eu2+（b）[5］，and their correlation in phosphors including halide，oxide，sulfide，and selenide compounds（c）[28］.The crystal field splitting of the 5d configuration of Ce3+（d）and Eu2+（e）in nitride phosphors[6］.（f）Coordination environment of Ce3+/Eu2+.L is the ligand，F-，S2-，N3-and so on，CN is the coordination number，Rradi is the ionic radius of central ion，RPECM is the average distance between ligand and central ion，Reff is the effective distance between ligand and central ion[6］.

關于晶體場劈裂，可通過點電荷靜電模型（PCEM）進行計算和解釋。八面體、立方體和立方八面體配位多面體分別包含一個上下表面有0，2或6個配體的三棱柱和反三棱柱[30]。G?rller-Walrand等提出晶體場參數B20和B40可以表達為

其中Z為配體電荷，R為鍵長，r為離子半徑，P為三次對稱軸平面的數量，n是垂直三次對稱軸的平面數量。θpr是三次對稱軸和從原點到6個棱柱頂點陰離子的矢量之間的夾角。括號中的表達式表示角部分Θkq，描述了陰離子的幾何構型對晶體場參數的影響。八面體、立方體和立方八面體配位的Θ20約等于0，Θ40分別為-2.33，2.07，1.17，比值為1∶0.89∶0.5，和以上使用經驗公式擬合得到的結論基本一致。

晶體場劈裂的大小與陰離子的類型無關，而主要取決于配位多面體的幾何構型，即點電荷靜電模型中的角部分Θkq。然而，根據Bkq的表達式可以看出Bkq和配位電荷Z成正比。即在點電荷靜電模型中，晶體場劈裂應該和配位陰離子的電荷有關，這和使用經驗公式分析擬合得到的結果相矛盾。我們課題組提出使用陰離子的有效電荷Z=Q/N（Q（Ce3+）=3，Q（Eu2+）=2）代替形式電荷Z（鹵化物為1，硫化物和氧化物為2，氮化物為3）可以有效解釋這一矛盾。圖3（f）繪制了有效電荷概念示意圖，其中N個配位離子分別攜帶Q/N個有效電荷。所以Bkq中的配位電荷Z與陰離子的類型無關，而是與Ce3+和Eu2+陽離子的電荷成比例。此外，Eu2+和Ce3+電價之比為2/3=0.67，根據點電荷靜電模型，Eu2+5d能級晶體場劈裂應為Ce3+5d能級晶體場劈裂的0.67倍，這一數值與統計分析得到的0.76十分接近。因此,有效電荷的概念也可以在一定程度上幫助理解Eu2+的晶體場劈裂小于Ce3+的晶體場劈裂的原因[6]。

值得關注的是，晶體場劈裂不僅取決于發光中心與配體的距離r，還取決于配位多面體的幾何構型，即角部分[31-32]。在晶體材料中，配位多面體相互之間通過共頂點、共棱或共面連接[33]。通過摻雜通常引起本身和相鄰配位多面體形狀和大小的協同變化，導致晶體場劈裂出現復雜的變化規律，比如在YAG∶Ce3+材料體系中[34-36]。深入理解這些變化規律，需要對局域結構和晶體場進行深入的分析。將質心移動與晶體場劈裂理論相結合，可以幫助預測和調控Ce3+/Eu2+摻雜的無機發光材料的吸收光譜和激發光譜。

2.3 誘導效應對電荷遷移帶和fd躍遷發光的影響

Ce3+/Eu2+5d能級作為決定其發光性能的重要因素，主要取決于基質的組成和結構。5d能級的質心位置主要取決于電子云擴展效應的影響，即由材料整體的組成和平均結構決定。此外，局域結構也對5d能級的能量位置有重要影響。最近鄰配位陰離子對5d能級的影響，即晶體場劈裂，廣泛用于理解和預測材料的發光性能。然而，次近鄰陽離子對5d能級能量的影響，即誘導效應，卻很少被關注。如圖4（a）所示，對于三元化合物TxMyXz，其中X為陰離子，T和M為陽離子。如果T電負性小于（或電正性大于）M，那么T較M來說更傾向于成為電子施主而提供電子，該電子會影響M—X鍵的電子云分布，即陰離子X更傾向于得到來自陽離子T的電子而不是陽離子M的電子，M—X鍵類型必定會發生一定程度的變化，這個現象被稱之為誘導效應[37]。

圖4 （a）金屬元素M的誘導效應機理圖[40］；（b）三元/四元硅氮化合物中Ce3+5d能級質心移動εc和誘導因子μΔχ的關系[40］；（c）誘導效應：KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+中Eu2+最低5d能級與d22/d12比值隨x值的變化關系[43］。Fig.4（a）Schematic diagram of the inductive effect of M.The thickness of arrow represents the degree of ability of donating electrons[40］.（b）Centroid shift of 5d levels of Ce3+versus the inductive factor in（qua）ternary nitridosilcates[40］.（c）Inductive effect：lowest 5d energy level and the ratio of d22 to d12 as functions of the x values in KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+[43］.

誘導效應在有機化合物中被廣泛應用，隨后Noll[38]首次引入到無機固體中用來解釋硅酸鹽中Si—O鍵 的 變 化。1992年，Etourneau等[37]采 用 誘導效應概念來解釋無機化合物的包括氧化還原勢、電導率、磁學性質、光學性質等的變化。2017年，Xiao等將誘導效應的概念引入至Ce3+/Eu2+摻雜 無 機 發 光 材 料 中，用 于 解 釋K2（0.995-x）Na2xAl2B2O7∶0.01Eu2+的可調控發光性能。激發光譜分析顯示Eu2+5d能級的質心移動隨著x的增大而減小，Xiao等使用誘導效應對這一現象進行了解釋[39]。2018年，我們課題組對硅氮/氧化合物中誘導效應對局域結構和發光性能的影響規律進行了系統研究[40-41]。

電負性是理解誘導效應的重要參量，Pauling將電負性描述為“分子中原子吸引電子到自身的能力”；Leach將電負性描述為元素的基本屬性[42]。我們課題組從結構化學角度出發，采用統計學方法，通過研究上百種硅氮/氧化合物的晶體結構和光譜數據，提出了關鍵參數——誘導因子μΔχ，定量化研究了次近鄰陽離子的誘導作用[39]。發現[SiN4]或[SiO4]四面體的加權平均鍵長以及Si原子加權平均鍵價與誘導因子呈明顯線性關系。金屬在硅氮化合物中的誘導效應要明顯強于硅氧化合物。同時，發現Ce3+5d能級質心移動εc大小與誘導因子μΔχ正相關，如圖4（b）所示。

誘導效應也可以用于理解分析電荷遷移帶的變化規律[41]。稀土離子電偶極允許的躍遷分為兩種：電荷遷移（Charge transfer,CT）躍遷和4fn-4fn-15d躍遷。前者像是從配體得到一個電子被還原，例如四價離子Ce4+、Pr4+和三價離子Sm3+、Eu3+、Yb3+傾向于得到電子變成相應三價和二價離子，光譜上表現為電荷遷移吸收帶；而后者的4f-5d躍遷像是失去電子被氧化的過程，例如三價離子Ce3+、Pr3+和二價離子Eu2+、Sm2+、Yb2+傾向于變成相應的四價和三價離子，光譜上表現為4f-5d吸收帶。在很多三價稀土離子摻雜的化合物中，三價稀土陽離子得到配位陰離子的電子而成為二價陽離子，光譜上表現為寬帶吸收，稱之為電荷遷移帶。從誘導效應角度來看，如果稀土陽離子配位多面體外的次近鄰陽離子的電負性不同，將影響陰離子的電荷分布，從而影響電荷遷移過程難易程度，在光譜上表現為電荷遷移帶的紅移或藍移。反之，電荷遷移帶的位置也必然反映出稀土離子局域結構環境。我們通過分析三價稀土離子摻雜無機固體的電荷遷移帶以及晶體局域結構相關信息，研究了在電荷遷移過程中晶體局域結構的誘導作用，提出次近鄰配位陽離子的兩個重要誘導參數——電負性因子和離子半徑因子，從而半定量化研究了次近鄰陽離子通過誘導效應對稀土離子電荷遷移帶的影響規律。通過將次近鄰陽離子按照晶體學格位種類進行分類，討論了一種、兩種、三種以及更多種類次近鄰陽離子發生改變時的電荷遷移帶能量變化。研究發現，電荷遷移能與電負性呈負相關關系，而與離子半徑呈正相關關系[36]。

誘導效應與最近鄰陰離子和次近鄰陽離子的距離和幾何構型密切相關。例如，我們發現在KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+固溶體中，Eu2+最低5d能級與d22/d12比值密切正相關，該現象可用誘導效應來解釋[43]。當Eu2+取代了M2格位時，沿鏈方向的最近鄰的陽離子之間的距離（d22=0.392 8 nm）小于鏈間兩最近鄰的陽離子的距離（d12=0.420 1 nm）。因此，最近鄰的Ba更易于貢獻出一個電子，并對Eu—O施加更多的電子壓力，這就使得Eu—O的共價性有所上升。因此，沿鏈方向的5d軌道就會具有更低的能量，成為最低5d能級，并決定了最低激發帶的位置。在KxBa1.97-x（Si1-xPx）O4∶0.03Eu2+中，隨 著x值 的 增加，d22逐漸增加而d12逐漸減小，如圖4（c）所示。因此，沿鏈方向形成的d軌道能量升高，引起激發 峰 的 藍 移。對 于 端 元 成 分KBaPO4∶Eu2+，d22幾乎等于d12，這就導致了鏈狀效應的消失，最低激發峰也具有最大的藍移[43]。

2.4 電聲子耦合和斯托克斯位移

斯托克斯位移ΔS即為相同電子態間電子躍遷的吸收和發射能量的差值。基于晶體場劈裂和質心移動可以根據化合物的組分及結構預測熒光粉的激發譜位置，在此基礎上結合斯托克斯位移則可以進一步預測熒光粉的發射譜位置。

對于Ce3+/Eu2+摻雜無機化合物，斯托克斯位移是最低5d能級和4f基態能級之間吸收和發射能量的差值。斯托克斯位移源于電聲子耦合，可用位形坐標模型進行描述[38]，如圖5所示。基于以下兩個假設：（1）Born-Oppenheimer近似，即摻雜離子內電子轉移的光學躍遷發生得很快以至于在躍遷過程中晶格不發生弛豫；（2）僅考慮一種晶格振動模式，呼吸振動模式。同時假設基態和激發態振動頻率相同。因此，斯托克斯位移ΔS可表達為[44]

其中?為約化普朗克常數；ω為振動圓頻率；?ω是連續振動能級之間的能量差，即為聲子能量；無量綱黃昆因子S表示電子態和振動態的耦合程度，即電子-聲子耦合程度。公式（13）廣泛應用于Ce3+/Eu2+摻雜熒光粉的斯托克斯位移的計算和分析[20,45-46]，然而，近年來另一公式ΔS=2S?ω出現在一些研究報道中[47-48]。Jong等系統地研究了這一問題，發現這兩個表達式都是近似正確的，實際的斯托克斯位移位于兩個公式的計算結果之間[19]。Blasse等對電子-聲子耦合程度進行了分類，定義S＜1為弱耦合，1＜S＜5為中耦合，S＞5為強耦合[49]。黃昆因子S的計算公式為：

其中α=Mω/?，M為振動系統的約化質量。ΔQe為晶格弛豫；電子被激發到激發態時，電子云分布的改變致使核處于一個新的平衡位置，平衡位置的變化量稱為晶格弛豫ΔQe，如圖5所示[19,44]。晶格弛豫ΔQe取決于化合物中鑭系離子替代的陽離子種類、配位陰離子種類以及局域結構。Blasse等報道在三個正硼酸鹽中，鑭系離子所替代的陽離子越大，斯托克斯位移越大[50]。此外，如公式（13）所示，聲子能量?ω和斯托克斯位移正相關。文獻報道聲子能量在鹵化物體系中按氟化物（～350 cm-1）到氯化物（～260 cm-1）到溴化物（～200 cm-1）的順序依次減小[51]。氧化物（～600 cm-1）比硫化物（～270 cm-1）具有更大的聲子能量，硒化物（150 cm-1）聲子能量最小[52]。這些結果表明晶格振動頻率ω按照從氧化物到硫化物到硒化物的順序依次降低。在鹵化物體系中按照從氟化物到氯化物到溴化物的順序依次降低。這是由于原子質量增加，原子半徑增加，電負性降低以及鍵合強度變弱，從而晶格振動頻率降低。

圖5 Ce3+/Eu2+質心移動、晶體場劈裂和斯托克斯位移示意圖，圖中注明位形坐標模型中的振動能級和聲子能量[7］。Fig.5 Energy level diagram showing the crystal field splittingεcfs，centroid shiftεc and the Stokes shiftΔS.The vibrational states and phonon energy are indicated in the configurational coordinate diagram[7］.

為進一步探索Ce3+/Eu2+摻雜無機發光材料的斯托克斯位移和基質材料組成以及結構之間的相關關系，我們課題組收集整理了60多種Ce3+/Eu2+摻雜無機發光材料的結構和光譜數據，系統研究了Ce3+/Eu2+取代的陽離子和配位陰離子特性對斯托克斯位移ΔS、聲子能量?ω和黃昆因子S的影響[7]。化合物選取原則是：稀土離子占據單一晶體學位置，是單一發光中心，以便排除多發光中心由于光譜重疊對斯托克斯位移數據讀取帶來的誤差。結果表明Ce3+/Eu2+取代的陽離子和配位陰離子特性對斯托克斯位移ΔS、聲子能量?ω和黃昆因子S有重要影響。斯托克斯位移和有效平均配位鍵長Rav正相關。在鹵化物和硫屬化合物中，斯托克斯位移分別按照從氟化物到氯化物到溴化物和從氧化物到硫化物到硒化物的順序依次降低；然而，在具有同一周期陰離子的化合物中，斯托克斯位移和陰離子類型沒有明顯的相關關系。在大多數情況下，聲子能量和平均配位鍵長R負相關，而黃昆因子和平均配位鍵長正相關。此外，結果表明斯托克斯位移和陽離子配位數沒有明顯的相關關系。

在具有相同結構和陰離子類型的化合物中，黃昆因子S和平均配位鍵長R正相關，而聲子能量?ω和平均配位鍵長R負相關。根據公式（14），黃昆因子S和晶格弛豫ΔQe正相關，晶格弛豫ΔQe即為電子被激發到激發態時電子云分布的改變使核的平衡位置發生的變化。因此，晶格弛豫ΔQe和化合物中陰離子與中心陽離子之間的配位鍵長密切相關。在鑭系離子取代中心陽離子時，鑭系離子在具有較長配位鍵長的基質材料中有較大的容納空間，使電子在從基態躍遷到激發態時具有更寬松的空間調整其平衡位置，導致材料具有較大的晶格弛豫ΔQe。因此黃昆因子S和晶格弛豫ΔQe與平均配位鍵長正相關。由于斯托克斯位移和平均配位鍵長具有同樣的正相關關系，因此，黃昆因子在斯托克斯位移和平均配位鍵長的正相關關系中起主導作用。

在具有相同結構和陽離子的化合物中，聲子能量?ω在鹵化物和硫屬化合物中分別按照從氟化物到氯化物到溴化物和從氧化物到硫化物到硒化物的順序依次減小，和斯托克斯位移與陰離子類型之間的相關關系一致。這一現象可以使用位形坐標模型進行理解。在晶格弛豫ΔQe相同的情況下，較大的振動頻率使勢能曲線的曲率較大，從而導致較大的斯托克斯位移。另一方面，原子質量在鹵化物和硫屬化合物中分別按照從氟到氯到溴和從氧到硫到硒的順序依次增加，使得原子半徑增加，電負性降低，從而導致中心陽離子和配位陰離子之間的化學鍵具有較軟的屬性。較大的陰離子質量和較軟的化學鍵屬性使基質材料晶格的振動頻率較小，導致其較小的聲子能量。

在具有同一周期陰離子的化合物（例如氟化物、氧化物和氮化物）中，斯托克斯位移不隨陰離子種類的改變而改變。如上所述，斯托克斯位移主要取決于鑭系離子占據空間位置的大小和結合鍵的強度。前者較易理解，因為同一周期元素具有相似的原子半徑。然而同一周期中陰離子配體的電荷對斯托克斯位移幾乎沒有影響，可以通過有效電荷的概念對其進行理解，即使用陰離子的有效電荷Z=Q/N（Q（Ce3+）=3，Q（Eu2+）=2）代替形式電荷Z（鹵化物為1，硫化物和氧化物為2，氮化物為3）[53]。

斯托克斯位移和陽離子的配位數沒有明顯的相關關系。這與晶體場劈裂不同，由于陰離子配體幾何構型的影響，晶體場劈裂和陽離子配位數有明顯的相關關系。斯托克斯位移主要取決于晶格弛豫ΔQe和勢能曲線的曲率。一般情況下，較多的配位陰離子使發光中心在基質材料中占據較大的空間位置，因此電子在從基態躍遷到激發態時具有更寬松的空間調整其平衡位置，導致材料中晶格弛豫ΔQe較大。同時，空間越寬松，位形坐標模型中勢能曲線的曲率越小。晶格弛豫ΔQe和勢能曲線的曲率共同作用、相互抵消，使斯托克斯位移和陽離子配位數沒有明顯的相關關系[7]。

需要注意的是，用位形坐標模型去描述電聲子耦合有一個假設：即僅考慮一種晶格振動模式，呼吸振動模式。顯然，該模型做了簡化處理，在用來理解斯托克斯位移與組分和結構的關系時，可能得不到滿意的解釋。另外，當發光中心離子進入晶格后，由于晶格弛豫，會引起局域結構的復雜變化。因此，需要考慮局域結構的變化對斯托克斯位移的影響，從而解釋對發射光譜移動的影響規律[8,43,54]。另外，通常隨著激活離子濃度的增加，發射光譜由于晶體場的變化和重吸收效應發生紅移，斯托克斯位移變大[55]。

2.5 發光效率、發光熱猝滅、缺陷和長余輝發光

發光材料的內量子效率定義為發射光子數和吸收光子數之比[56]。當電子從基態激發到激發態后，可以通過兩種途徑返回基態，分別為輻射躍遷和非輻射躍遷。輻射躍遷即指發光，非輻射躍遷則指能量以除發光以外的形式耗散掉，通常又稱為發光猝滅[57]。因此，輻射躍遷速率和非輻射躍遷速率二者之間的比值決定了熒光粉的發光效率。通常非輻射躍遷有多種通道，源于不同的物理機制。

目前，學者們普遍認可的Ce3+/Eu2+摻雜無機發光材料的發光猝滅機制或非輻射躍遷過程主要有三種：基于位形坐標模型的基態和激發態的交叉弛豫、基于材料電子結構的5d電子到導帶的離化、以及雜質和缺陷導致的發光猝滅[58-61]。對于位形坐標模型，足夠的熱能可以幫助激發態電子達到較高的振動能級。如果這一振動能級到達或高于基態和激發態勢能曲線的交點，激發態電子則借助聲子（晶格振動）釋放能量通過交點回到基態，導致發光猝滅[15,61]。由于勢能曲線的交點位置取決于材料的聲子能量?ω和黃昆因子S，所以在位形坐標模型中，熒光粉的室溫發光效率和熱猝滅特性主要由材料的聲子能量?ω和黃昆因子S決定。研究發現剛性結構有助于抑制發光猝滅從而實現較高的發光效率，并提出使用德拜溫度判定材料的結構剛性[62]。在電子離化模型中，5d1激發態電子可以被光電離或熱電離至導帶。隨后，離化電子非定域化并在整個晶體中移動，這增大了其被缺陷陷阱捕獲的概率，從而導致發光猝滅[59,63]。在電子離化模型中，發光效率和發光熱猝滅特性主要取決于5d電子的離化能，即5d電子能級和基質化合物導帶底的能量差。在雜質和缺陷導致發光猝滅模型中，激發態能量可以傳遞到缺陷（包括表面缺陷）或雜質能級，從而導致發光猝滅。這種傳遞的發生僅限于雜質或缺陷與激活劑離子足夠接近的情況，或激活劑離子的濃度足夠高。隨著激活劑離子濃度增加和隨溫度升高，激活劑離子之間能量傳遞增強，輻射躍遷概率減小，非輻射躍遷概率增加（例如，能量傳遞到雜質或缺陷能級的概率增強），從而導致發光猝滅，這一過程與濃度猝滅密切相關[61]。值得注意的是與這些雜質和缺陷相關的猝滅過程不是材料固有的，可以通過優化合成條件減少缺陷和雜質濃度以及改變發光中心濃度等方法來提高材料的發光效率和抗熱猝滅特性。與位形坐標模型和電子離化模型相關的發光熱猝滅是材料的固有特性；與4f和5d勢能曲線的交點以及激活劑離子5d能級相對于基質導帶底的相對能量位置相關。人們可以通過合適的基質化合物、或對已有熒光粉進行改性，來調控電聲子耦合和電子結構，從而提高其發光效率和抗熱猝滅性能[58-61,64-65]。

基于位形坐標模型的基態和激發態的交叉弛豫過程中，激發態電子直接回到基態，導致發光熱猝滅。基于材料電子結構的5d電子到導帶的離化過程，激發態電子沒有回到基態，而是被激發到導帶中或被電子陷阱捕獲；隨著溫度升高，這部分電子被熱激發通過導帶回到5d態，再躍遷到4f基態發光。這通常導致在測量過程中，發光強度隨溫度升高而增強，使得材料表現為發光零熱猝滅或熱猝滅反常[9]。另一方面，這部分被陷阱捕獲的電子如果在室溫下被熱激活就會導致長余輝發光，在光激勵下被激活就會導致光激勵發光。

在高性能熒光粉基礎上，基于電子結構，通過調控帶隙、5d能級與導帶底的能量差、缺陷類型、缺陷深度和濃度，可實現長余輝發光和光激勵發光。例 如，在Y3Al5O12∶Ce3+中，通 過Ga替 代Al調控帶隙，摻雜Yb3+、Cr3+、B3+等引入合適的陷阱，獲得了優異的黃綠超長余輝發光材料[66-69]。在（Ba,Sr）3SiO5∶Eu2+中通過摻雜Ge調控帶隙，引入Nb5+獲得合適的陷阱，制備出了可被太陽光激發的暖色調超長余輝發光材料（圖6（a）～（d））[70-72]。對于（Ca,Sr）AlSiN3∶Eu2+、β-Sialon∶Eu2+和SrLiAl3N4∶Eu2+，最低5d與導帶底的能級差較大；可利用短波長的激發光，把Eu2+的基態4f電子直接激發到導帶，隨后被陷阱捕獲，實現長余輝發光或光激勵發光。這些材料的余輝激勵過程與SrAl2O4∶Eu2+,Dy3+長余輝發光的激勵過程明顯不同（圖6（e）～（f））[73-75]。

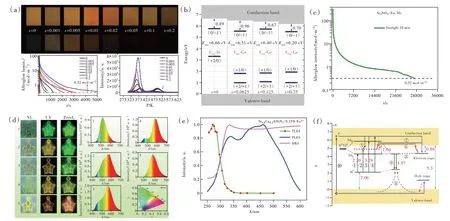
圖6 （a）Sr3（Si1-xGex）O5∶Eu2+（x=0～0.2）的余輝性能[70］；（b）Sr3（Si1-xGex）O5（x=0，0.062 5，0.125，0.25）中氧空位的熱力學電荷轉移能級示意圖[70］；（c）Sr3SiO5∶Eu2+，Nb在陽光下照射10 min后的余輝衰減曲線[71］；（d）SrAl2O4∶Eu2+，Dy3+和Sr3SiO5∶Eu2+，Nb封裝器件余輝性能示意圖[71］；Sr0.8Ca0.2AlSiN3∶Eu2+的余輝激發光譜（e）和余輝機制（f）[73］。Fig.6（a）The persistent luminescence properties of Sr3（Si1-xGex）O5∶Eu2+（x=0-0.2）[70］.（b）Calculated thermodynamic charge transition levels for the most stable oxygen vacancies in Sr3（Si1-xGex）O5（x=0，0.062 5，0.125，0.25）[70］.（c）Persistent luminescence decay curve of Sr3SiO5∶Eu2+，Nb after sunlight irradiation for 10 min[71］.（d）Persistent luminescence property of devices fabricated with SrAl2O4∶Eu2+，Dy3+and Sr3SiO5∶Eu2+，Nb[71］.（e）PLE，TLE and DR spectra of Sr0.8Ca0.2AlSiN3∶0.15% Eu2+[73］.（f）Persistent luminescence mechanism for Sr0.8Ca0.2AlSiN3∶xEu2+[73］.

發光材料的熱穩定性、長余輝發光和光激勵發光與材料的電子結構密切相關。因此，深入理解稀土摻雜無機化合物的電子結構對設計研發高效發光材料、長余輝發光材料和光激勵發光材料等具有重要意義。

2.6 稀土摻雜無機化合物的電子結構

稀土摻雜發光材料的發光性能，包括激發和發射譜的位置、發光熱穩定性、閃爍性能以及長余輝性能等，主要取決于稀土離子相對于基質材料導帶底和價帶頂的電子能級結構[76]。2003年，Dorenbos在Dieke圖的基礎上，結合光譜數據和稀土離子電子結構信息構筑電子結構圖，給出了二價、三價稀土離子的4f、5d各能級相對于基質化合物導帶底和價帶頂的能量位置以及它們相對于真空的能量位置，稱為HRBE圖（Host referred binding energy）和VRBE圖（Vacuum referred binding energy）[77-79]。

圖7為LaF3的HRBE圖 和VRBE圖[26]。圖 中雙“之”字形曲線①和③分別連接二價稀土離子Ln2+和三價稀土離子Ln3+的4f基態電子能量，曲線②和④分別連接Ln2+和Ln3+的最低5d激發態電子的能量。大量的理論和實驗證明，在所有的無機化合物中，HRBE圖中四條曲線的形狀幾乎不變[80]。基于自由二價和三價稀土離子的電離能數據，使用化學位移模型、鑭系收縮模型以及大量的實驗數據進行修正，2017年，Dorenbos給出電子結構圖曲線形狀參數[80]。因此，電子結構圖的構筑主要基于化合物依賴的3個參數：（1）基質化合物導帶底和價帶頂之間的能量差，即帶隙能量Eg（箭頭a）；（2）Ln2+的4f基態相對于基質價帶頂的能級位置（箭頭b）；（3）Eu2+和Eu3+基態4f電子能量的能量差U（6，A）（箭頭c）[53]。基質化合物的帶隙Eg可以由激子能量Eex得到，根據經驗公式

圖7 LaF3的HRBE圖和VRBE圖[26］Fig.7 HRBE and VRBE diagrams of LaF3[26］

其中激子能量Eex可以通過紫外漫反射或真空紫外激發光譜得到[26]。Ln2+的4f基態相對于基質帶隙的能級位置，目前主要有三種獲得途徑。一是通過激發使電子直接從價帶進入Ln3+的4f殼層，使Ln3+變 為Ln2+，即 電 荷 遷 移（Charge transfer）。Ln3+的電荷遷移帶（Charge transfer band）峰位對應的能量即為價帶頂和Ln2+的4f基態能級之間的能量差[77]。第二個方法為通過光子激發Ln2+，使電子從4f基態直接進入導帶，并檢測光電流強度。相應峰位對應的能量即為Ln2+的4f基態能級和導帶底的能量差[81]。最近，我們課題組提出了第三種方法，即利用某些化合物的余輝激發光譜的起始能量作為4f基態與導帶底的能量差以確定Eu2+（或Ce3+）的4f能級位置[73-74]。Eu2+和Eu3+基態4f電子能量的能量差稱為U（6，A），即4f電子間庫倫排斥能[82]。由 于U（6，A）與Ce3+5d能級質心移動εc（1,3+,A）都取決于晶格中稀土離子周圍的配位環境，2013年Dorenbos在大量實驗數據的基礎上提出使用εc（1,3+,A）計算U（6，A）的經驗公式[26,83]

當Ln2+和Ln3+的4f基態能級位置確定后，通過光譜數據，可以較容易地得到其最低5d激發態電子的能級位置，完整地繪制出HRBE圖。隨后，Dorenbos建立了化學位移模型[53]。基于Eu2+的4f電子和周圍化學環境的交互作用，假設周圍電荷平均分布，得到化學位移值E4f（7,2+,A），即在化合物A中Eu2+的4f電子電離能，與U（6，A）的關系公式[53,84]

由于各鑭系離子之間4f以及5d能級的相對能量在化合物中保持不變，所以根據化合物中Eu2+4f電子電離能可以得到該化合物中所有二價和三價鑭系離子的4f以及5d電子的電離能，完整地繪制出VRBE圖。

HRBE圖和VRBE圖提供14種二價、三價稀土離子的4f、5d能級和基質化合物電子結構的能量信息。電子結構圖不僅可以預測14種稀土離子的能級結構、材料帶隙結構和稀土離子價態，而且可以幫助我們通過調節鑭系離子基態、激發態能級和基質晶格價帶、導帶的相對位置，改善稀土摻雜無機發光材料的發光性能[85]。

提供各稀土離子能級結構。在化合物中，只要得到任何一種稀土離子的能級結構信息，根據曲線形狀參數，可以直接預測其他13種稀土離子在該化合物中的能級結構。

給出基質化合物價帶頂和導帶底的能量位置。VRBE提供稀土離子4f和5d能級，以及基質價帶頂和導帶底相對于真空（0 eV）的能量信息，這使得所有基質化合物處在價帶頂和導帶底的電子能量具有可比性。我們可以得到不同化合物價帶頂和導帶底電子能量隨其化學組成和結構的變化規律，從而用于分析和預測化合物的電子結構和性能，同時幫助設計滿足應用需求的新型發光材料。

預測稀土離子的穩定價態。Dorenbos假定費米能（Ef）位于導帶底和價帶頂的中間位置。進一步假設少量稀土摻雜幾乎不影響化合物的費米能，則低于費米能的能級應被占據，而高于費米能的能級應被閑置，即稀土離子價態取決于Ln2+4f基態電子電離能和費米能級的能量差（EFf=E4f（Ln2+）-Ef）。若化合物中EFf＜0,則稀土離子傾向于以二價態存在；若EFf＞0,則稀土離子傾向于以三價態存在[86]。

解釋發光熱猝滅特性。發光熱穩定性和Ce3+/Eu2+激發態5d電子到導帶底的能量差密切相關。5d電子到導帶底的能量差越小，越容易離化到導帶，發光熱穩定性越差。電子能級結構圖可以提供5d電子和導帶底的相對能量位置，因而可以幫助我們理解分析以及設計調控材料的發光熱穩定性。例 如，SrMg2Al2N4和SrMg3SiN4與SrLiAl3N4三個化合物晶體結構盡管空間群不同，但結構骨架非常相似，即具有Vierer環狀骨架結構。我們基于光譜數據，構筑了這三個化合物的HRBE及VRBE圖，闡明該系列熒光粉的發光熱焠滅特性與機制[8]。

調控閃爍材料的性能。無機閃爍材料廣泛應用于電離輻射探測領域。為了最大程度消除能量累積造成的重影，閃爍材料要求具有較快的衰減時間。材料中缺陷的存在會延長其衰減時間，因此，我們可以利用電子能級結構圖，調節材料帶隙和缺陷能級之間的相對能量，設計調控閃爍材料的性能[87]。

設計和調控長余輝發光材料的性能。HRBE圖和VRBE圖不僅為分析材料的長余輝機理提供依據，同時提供兩種調控長余輝發光材料的長余輝性能的途徑，分別稱為能帶工程和缺陷工程。能帶工程即通過陰/陽離子取代的方式，改變基質材料的帶隙，從而改善其長余輝性能。缺陷工程即通過選擇合適的稀土摻雜離子，調控陷阱能級與基質帶隙能級結構的相對位置，調節長余輝發光材料的長余輝性能[68,88]。

3 局域結構與發光性能調控

由于5d軌道受配位環境的影響大，因此局域結構對Ce3+/Eu2+摻雜無機發光材料的性能有重要影響。前文也表明局域結構與晶體場劈裂、誘導效應、斯托克斯位移、發光效率和發光熱猝滅等密切相關。

X射線衍射分析（XRD）是測定無機材料晶體結構最重要的技術手段，但其主要表征的是具有周期性的平均結構，對局域結構的分析還需要結合其他方法，如透射電鏡[89]、晶體學和固體化學的知識[90-91]。另外，由于固體中稀土或過渡族金屬離子的發光對局域結構的變化非常敏感，因此可通過光譜分析來推測局域結構[24,54]。例如，對于Ce摻雜的SrYSi4N7熒光材料中Ce3+的晶體學位置，存在兩種看法：一是Ce3+被認為占據堿土金屬離子Sr2+的位置，二是被認為占據Y3+位置。兩種看法都有一定的依據，而且由于Ce3+離子的摻雜量通常較小，很難通過常規手段比如XRD測定具體占位。但是，借助光譜與成分和結構的關系式，通過Ce3+摻雜的SrYSi4N7的光譜性能，來推測Ce3+離子的真實占位。結果表明Ce3+離子在SrYSi4N7中，占據的是Sr2+位置[24]。

熒光粉通常是粉末材料，而粉末衍射數據由于顆粒擇優取向等因素，會導致衍射強度出現偏差，從而影響基于Rietveld結構精修方法解析原子占位和占有率的準確性。因此，用XRD來測定摻雜濃度較低的原子占位具有較大不確定性。另外，XRD很難分辨原子序數相近的原子或離子。但是，XRD對于晶格常數的測量和分析通常具有很小的誤差，因此有時可利用晶格常數的變化來分析晶體結構。例如，對于Sr2-2xEu2xSi5N8熒光粉，盡管Sr2+離子半徑（0.121 nm，7配位）與Eu2+離子半徑（0.120 nm，7配位）相差非常小，但即使用很少量的Eu2+替代Sr2+，也會在實驗上測量到晶格常數的減小[55]。例如，我們基于晶格常數隨成分的變化并結合結構化學知識確定了氧原子在CaAl-SiN3∶Eu2+結構中的占位[90]。

分析局域結構通常需要晶體學和固體化學的知識。晶體學將晶體中具有周期性規則排列的原子位置抽象為格位（Site）。每一種空間群都包含若干種格位，這些格位的對稱性（Site symmetry）各不相同，一般用Wycokff符號加以區分。該符號由數字和字母構成，其中數字表示多重度（Multiplicity），即一個單胞中該格位的等效數目；字母用來表示對稱性的高低。例如，對于Y3Al5O12,按照晶體學位置可表述為{A}3[B]2（C）3O12，{A}代表8配位十二面體的24c格位，[B]為6配位八面體的16a格位，（C）為4配 位 四面體 的24d格 位[33]。Ga替代Al時優先占據24d格位，也可占據16格位。由于存在反位缺陷，部分Y可以占據[B]位，部分Al則可占據{A}位置。格位是由對稱性而非化學元素所決定的；同一種原子可以占據不同的格位，而不同的格位可以容納相同的原子。因此，用元素符號表示格位容易引起混淆，可用其他符號表示。例如，在（Sr,Ba）SiO4∶Eu2+中有兩種4c格位，其原子坐標不同，且配位數分別為10和9。Sr和Ba在這兩種格位上雖存在擇優占位，但在兩個格位上均有分布；因此如果用“Sr位”或“Ba位”容易引起混淆。此時可單獨定義對應于10配位、9配位的M格位、M’格位來描述具體的占位情況[15]。在T相（Ba,Ca）2SiO4∶Eu2+的晶體結構中，5個晶體學位置（Wyckoff site）發生了原子格位劈裂。這需要利用晶體學分析其局域結構。分析發現產生原子格位劈裂的原因是為了優化成鍵；這使該相結構剛性增強，從而導致了發光熱猝滅性能的提升[91]（圖8）。

圖8 T-相（Ba，Ca）2SiO4的晶體結構：（a）原子格位劈裂模型，（b）原子格位不劈裂模型，（c）發光熱猝滅特性[91］。Fig.8 Crystal structure of T-phase（Ba，Ca）2SiO4：（a）atom-split model，（b）atom-unsplit model，（c）thermal luminescent quenching characteristics[91］.

容忍因子（Tolerance factor）最早由Goldschmidt從鈣鈦礦結構中提出，它可以表征某一結構類型的晶體化學特征[92]。我們課題組通過結構分析和統計方法，構筑了石榴石、尖晶石和燒綠石系列化合物的結構容忍因子（圖9），為建立從成分出發計算預測結構和相穩定性的理論模型提供了重要的依據[33,93-94]。利用容忍因子快速判別具有特定化學組成化合物的相穩定性，避免了第一原理計算所需要的大量計算。另外，利用燒綠石型結構容忍因子還可以從成分出發計算預測燒綠石型化合物的原子有序-無序的占位[94]。結構容忍因子可為基于材料基因工程的理念和技術去計算和篩選化合物提供重要依據。

圖9 石榴石、尖晶石和燒綠石結構的容忍因子表達式[33，93-94］。Fig.9 Tolerance factors of garnet，spinel and pyrochlore structures[33，93-94］.

作為發光中心的稀土或過渡族金屬離子替代占據晶體中的某一格位后，由于與基質晶格中其他相同格位的化學元素不同，會導致晶格弛豫。替代后的配位多面體尺寸和形狀與原基質相比有所改變或調整。在晶體材料中，配位多面體相互之間通過共頂點、共棱或共面連接[33]。摻雜離子所處的配位多面體的調整受到周圍多面體的影響和制約，從而使局域結構分析變得困難和復雜。例如，在Cr3+摻雜的KMP2O7中，基質八面體格位M分別為Ga、Sc、In、Lu時，觀測到KMP2O7∶Cr3+材料源于Cr3+的發射峰的峰位和強度隨M的變化明顯不同，表明該結構中Cr3+替代后晶格弛豫較小[95]。然而，對于Sr9M（PO4）7∶Cr3+（M=Ga,Sc,In,Lu）熒光粉，所有樣品在485 nm光激發下在850 nm附近呈現一個寬帶近紅外發射峰位，發射峰位幾乎不隨M元素類型發生變化，表明該結構中Cr3+替代后晶格馳豫很大[96]：由于結構限域效應，盡管基質中M元素的離子半徑不同，但替代后Cr3+的配位多面體體積和形狀幾乎相同，因而發射峰位相同。

總之，局域結構對Ce3+/Eu2+摻雜無機發光材料的發光性能影響很大。局域結構的變化和分析具有復雜性。因此，需要綜合考慮發光理論、晶體學，并結合先進的結構和光譜分析技術，來理解發光材料的構效關系。下面我們以YAG∶Ce3+和CaAlSiN3∶Eu2+為例，說明局域結構與發光性能的關系。

3.1 鈰摻雜石榴石型發光材料

Ce3+摻雜石榴石結構熒光粉中的“反石榴石效應”是局域結構調控發光性能的一個典型例子。在（A24c）3{B16a}2[C24d]3O12中的三個陽離子格位分別替換較大半徑的離子，例如A位Gd替換Y∶（Gd）3{Al}2[Al]3O12→（Y）3{Al}2[Al]3O12,B、C位Ga替換Al∶（Y）3{Ga}2[Ga]3O12→（Y）3{Al}2[Al]3O12，都會導致晶格常數變大、多面體體積膨脹、平均鍵長增加等趨勢一致的平均結構變化規律。然而，前一種情況下晶體場劈裂變大，后一種情況下晶體場劈裂變小[31]。這一自相矛盾的現象無法用平均鍵長的5次方反比關系來解釋。實際上，對于互相連接的多面體，其中一個多面體的改變會造成鄰近多面體的協同變化，而正是這種協同變化造成了平均結構一致變化趨勢之下局域結構的差異。對于YAG中容納發光離子Ce3+的十二面體，Gd→Y和Ga→Al兩種替代方式會導致不同的配位遷移模式，如圖10（a）所示，并使十二面體產生沿不同方向的四方變形（Tetragonal distortion）[34]。晶體場分析表明，四方變形主導了Ce3+在石榴石結構中的晶體場劈裂[31,97-98]。我們通過多面體建模及晶體場定量計算的方式，研究上述十二面體的形變方式對于能級劈裂的影響。利用群論推導三價鈰離子在D4h和D2對稱性下的5d能級分布情況，發現最低和次低能級不再發生劈裂[99]。結果表明，石榴石晶體結構與三價鈰離子晶體場劈裂之間不再是簡單的五次方反比關系，而是與所占據的十二面體扭曲形變有關。石榴石結構中的三種陽離子多面體位的扭曲存在一種競爭關系，從而導致非均勻形變。對于Ce3+占據的多面體，雖然從平均結構上看多面體尺寸在增加，但相鄰多面體的協同變化導致了局域結構的不同，從而使晶體場劈裂表現出復雜的“反石榴石效應”。這也同時說明，用來判斷晶體場劈裂大小的5次方反比關系有局限性，不能以平均鍵長為唯一判斷依據，還應考慮配位彼此間的相對位置。

圖10 （a）YAG中不同格位替代導致的配位遷移模式[34］；（b）不同石榴石型化合物中晶體場劈裂與八面體面間距的對應關系[35］。Fig.10（a）Different ligand moving patterns caused by multiple site substitutions in YAG[34］.（b）Crystal-field splitting as a function of octahedral interplanar distance for different garnet series[35］.

我們課題組進一步嘗試從石榴石的結構特點出發，找到了能夠表征Ce3+晶體場劈裂的指示符[35]。不同石榴石熒光粉中晶體場劈裂與結構指示符的關系如圖10（b）所示，可見該指示符能夠較好地反映石榴中不同格位元素替代導致的晶體場劈裂變化，從而可以根據成分和結構預測相應材料的發光性能[35]。在YAG中，用氮替換氧能夠實現Ce3+發光的紅移。理論計算和晶體結構測定表明，氮元素替代后會擴張十二面體，造成Ce3+的晶體場劈裂增加，進而造成光譜紅移[36]。

3.2 局域結構對CaAlSiN3∶Eu2+系列固溶體發光性能的影響

CaAlSiN3∶Eu2+熒光粉在藍紫光區有寬的吸收帶，且發射紅光[54，90］。該熒光粉具有良好的化學穩定性和溫度猝滅特性，以及高量子效率，在白光LED中已得到應用。但是該熒光粉的發射主峰偏紅，大約在650 nm，致使采用其封裝的白光LED的光效偏低。為了進一步改善CaAlSiN3∶Eu氮化物熒光材料的發光特性，在CaAlSiN3∶Eu中摻入O調控其波長，使其藍移至與白光LED最匹配的620 nm。CaAlSiN3具有正交晶系結構，空間群為Cmc21，其 中Ca占 據4a位 置，Al和Si無 序 占 據8b位置，N原子占據兩種晶體學位置：8b和4a，分別標記為NI和NⅡ，單胞中NⅠ的數目是NⅡ的2倍。因此，CaAlSiN3的晶體化學式可以表示為Ca（Al-Si）2NI

2NⅡ。隨著O含量的增加，晶格常數a和晶格常數比a/b逐漸減小，而晶格常數b幾乎保持不變。根據晶格常數沿不同方向的變化規律不同，我們推定O原子在CaAlSiN3∶Eu結構中擇優替代NⅡ原子[90]。最終，我們將含O的CaAlSiN3的晶體化學式表達為Ca（Al/Si）2NI（2NⅡ1-xOx）。為了進一步調控A位和B位陽離子，我們課題組設計和制備 出 了（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+連 續 固溶體。通過XRD衍射圖譜及其晶格常數隨成分的變化圖可看出，樣品皆為純相。隨著x的增大，樣品的衍射峰向高角度方向移動，晶格常數相應線性變小，符合Vegard定律。從圖11（a）可以看出，激發光譜的高能端幾乎保持不動，而低能端隨著x增大而發生藍移。這意味著激發光譜的重心位置發生了藍移，光譜的半高寬（FWHM）變窄，即5 d能級的劈裂變小。在固溶體（C a 1-x L i x）（A l 1-x S i 1+x）N 3的晶體結構中，隨著x增大，晶格常數變小，單胞體積也相應變小。在這種情況下，E u 2+離子的5 d能級劈裂應逐漸增大，發射光譜紅移并逐漸加寬，這與觀察到的現象正好相反。我們認為這種異常現象有兩方面原因：一是E u 2+離子與配位的陰離子之間的距離沒有變小，反而為了容納更小的L i+離子，臨近的E u 2+所處的配位多面體變大；二是由于S i 4+替代A l 3+后化合物平均電負性發生改變，引起光譜極化率減小。該固溶體的發射光譜呈現了三個階段的變化過程，如圖1 1（b）～（d）所示。第一階段：隨L i/S i量的增加，發射光譜有微小藍移，從6 6 9 n m到6 6 3 n m；第二階段，從6 6 3 n m到7 3 8 n m的大幅度紅移；第三階段，當x=1時，發射光譜突然大幅度藍移至6 0 0 n m。通過對晶體結構和發光中心局域結構的分析，提出了如圖1 1（g）所示的模型來解釋化學成分連續變化時發射光譜不連續變化的現象。

圖11 （Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+（x=0～1）的發射光譜（a），及不同Li-Si替代量的激發光譜：（b）x=0～0.2，（c）x=0.3～0.9，（d）x=0.8～1；（e）光譜參數λc、λabs、λem和λ0隨x的變化規律；（f）斯托克斯位移隨x的變化規律；（g）（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+固溶體從CaAlSiN3（x=0）端元到LiSi2N3（x=1）端元的結構演化模型[54］。Fig.11（a）The excitation spectra of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+（x=0-1）samples with x=0-1，and the emission spectra of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+samples for different ranges：（b）x=0-0.2，（c）x=0.3-0.9，（d）x=0.8-1.（e）The wavelength ofλc，λabs，λem andλ0 as a function of x.（f）The Stokes shift as a function of x.（g）The proposed model on the chemical unit co-substitution strategy represented by structural evolution of（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+：from CaAlSiN3（x=0）to LiSi2N3（x=1）via the（LiSi）5+substitution for（CaAl）5+couple[54］.

在 固 溶 體（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+的晶體結構中，發光離子周圍由呈六圓環形狀排列的[AlN4]和[SiN4]四面體相間排列而成，有且只具有四種組合情況：3個[AlN4]和3個[SiN4]四面體（記為M1），2個[AlN4]和4個[SiN4]四面體（記為M2），1個[AlN4]和5個[SiN4]四面體（記為M3），以及全部6個[SiN4]四面體（記為M4），四種情況如圖11（g）所示。從M1到M4，發光中心離子的配位環境發生了從均勻到不均勻、再到均勻的變化情況。采用該模型能夠很好地解釋固溶體（Ca1-xLix）0.98（Al1-xSi1+x）N3∶0.02Eu2+的 發 光 特 性 隨成分的變化規律。

4 前景展望

Ce3+/Eu2+摻雜的無機發光材料由于其光譜可調、高內/外量子效率和高發光熱穩定性受到人們的廣泛關注，并具有廣泛的應用，如在LED照明和液晶背光源領域，以及作為長余輝發光材料和閃爍材料等。近年來，面向類太陽光LED健康照明和超高色域液晶顯示技術的發展，迫切需要研發新型高效深紅-近紅外發光材料[100-101]、紫光/藍光激發的全光譜LED照明用熒光粉[102-103]，以及窄帶發射的綠光和紅光發光材料[4,104]。但是，目前在這一領域仍存在一些問題，特別是在理論方面，需要人們深入研究和解決。

4.1 斯托克斯位移與材料組分和結構的定量關系

建立發光材料組分和結構與斯托克斯的相關關系對于預測熒光粉發射性能至關重要。受到熒光粉光譜數據數量和質量的限制，目前僅得到了材料組分和結構與斯托克斯位移的定性相關關系。因此，隨著Ce3+/Eu2+摻雜無機發光材料的實驗數據的積累、理論發展和計算能力的增強，深入探索材料組分、晶體結構和局域結構與斯托克斯位移之間的內在關系和電聲子耦合作用，將對新型高性能發光材料的研發提供科學依據。

4.2 發射帶半峰寬與材料組分和結構的關系

窄帶發射無機發光材料既可協同提升照明器件的顯色指數和流明效率（如窄帶紅色發光材料）,也可增大液晶顯示器件的色域（如窄帶藍色、綠色和紅色發光材料），在照明和顯示用發光二極管（Light-emitting diodes,LED）器件中具有重要的應用前景。因此研究發光材料組分和結構與半峰寬的相關關系將為研發新型窄帶發射無機發光材料提供重要指導。

4.3 發光效率和熱猝滅特性與組分和結構的關系

發光效率是評判熒光粉發光性能的重要參數，在熒光粉的實際應用中至關重要。研究發現剛性結構有助于抑制發光猝滅從而實現較高的發光效率，并提出使用德拜溫度判定材料的結構剛性[62]。然而，發光效率和熱猝滅特性與材料組分、晶體結構、局域結構和電子結構的定量關系尚不明確。因此探究影響發光效率的因素，揭示其與基質材料組分和結構的內在定量關系是今后研究的重要方向。

4.4 長余輝機理研究

目前，人們對長余輝發光材料的研究主要是通過實驗的手段，比如，通過摻雜調控帶隙或調控缺陷類型、缺陷的深度和濃度。通過第一性原理計算，也可分析材料的能帶結構、本征缺陷能級和摻雜離子能級結構。但目前對長余輝發光機理仍存在很多爭議。結合實驗數據，理論上深入研究長余輝發光機理，對研發新型高性能長余輝發光材料具有重要意義。

5 結 論

我們總結了近年來Ce3+/Eu2+摻雜無機發光材料的唯象理論和構效關系研究進展，特別是基質材料組分和結構與Ce3+/Eu2+5d能級質心移動、晶體場劈裂以及斯托克斯位移的相關關系的研究進展。同時總結了誘導效應、局域結構和電子結構對發光性能的影響規律；并通過論述熒光猝滅機理，總結了影響發光效率、發光熱猝滅特性和長余輝性能的因素。最后，對唯象理論和構效關系的未來發展提出了展望。

本文專家審稿意見及作者回復內容的下載地址：http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220191.