基于改進滑模控制的光伏并網逆變器 控制策略

米俊毅，趙興勇

（山西大學 電力與建筑學院，山西 太原 030006）

0 引言

近年來，為了解決化石能源帶來的環境惡化問題，充分利用可再生能源已成為國內外共識；以太陽能、風能為代表的可再生能源并網發電已經成為新型電力系統的發展趨勢[1,2]。

隨著光伏發電效率的提高、并網容量的增大，光伏逆變器的控制性能對于電網電能質量的影響愈加顯著，其控制策略的研究對于新型電力系統的發展具有重要意義[3,4]。

采用傳統的逆變器控制方法，如恒壓恒頻控制[5]、恒功率控制[6]、下垂控制[7]等線性控制方式[8-10]，雖能實現對逆變器的良好控制，但其對外界干擾的抑制效果較差，魯棒性能不足。

為了解決上述問題，多種非線性控制方法被應用于逆變器控制中。文獻[11]考慮了逆變器不確定參數和電網干擾，設計了一種電流環H∞魯棒控制器，但并未考慮電壓外環的控制性能以及直流側電壓的穩定性。文獻[12]將魯棒H∞控制技術和自抗擾控制相結合，提出了一種基于電網電壓定向的魯棒雙環控制策略，實現了對外界干擾所造成跟蹤誤差的有效抑制；但是，其控制器參數設計較為復雜，且嚴重依賴系統模型的精確性。文獻[13]將反步法與PI控制器結合，設計了一種非線性控制器，實現了電網與光伏發電系統間的功率平衡，但未考慮到電網電壓波動等外界干擾的影響。

光伏并網逆變器本身是周期性變結構系統。滑模控制策略（sliding mode control，SMC）因其具有很強的魯棒性，所以適用于光伏并網逆變器的控制[14]。文獻[15]設計了一種適用于中性點箝位型三電平逆變器的電流環滑模控制器，但其電壓環仍采用PI控制，抗擾動能力有限。文獻[16]根據有功無功誤差最小原則進行控制量的修正，提出一種離散滑模直接功率控制策略，但未考慮控制過程中的“抖振”現象。文獻[17]將滑模控制與自適應觀測器結合，通過調整系統切換函數的系數以削弱抖振，但是沒有詳細說明用于在線調整符號函數系統的自適應觀測器。

綜上分析，針對光伏并網逆變器存在直流側和網側不確定干擾的問題，本文提出一種雙閉環滑模控制策略：電壓外環采用積分滑模控制，以在穩定直流側電壓的同時減少系統穩態誤差；提出一種新型的趨近律用于電流內環滑模控制器，以在不犧牲系統響應速度的同時，盡可能地削弱系統抖振。

1 光伏并網逆變器模型

文中采用的光伏并網逆變器拓撲結構如圖1所示。

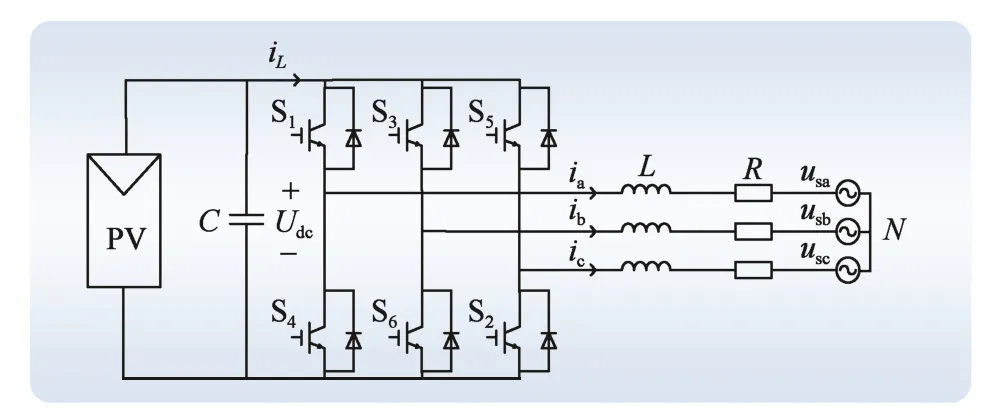
圖1 光伏并網逆變器拓撲結構圖 Fig. 1 Topology structure of photovoltaic grid connected inverter

圖1中：us表示電網相電壓；i表示逆變器交流側相電流；L和R分別表示逆變器交流側濾波電感的等效電感和內阻；C和Udc分別表示逆變器直流側電容和電壓。

為了簡化控制策略的設計，使用dq旋轉坐標系下的光伏并網逆變器數學模型[18]：

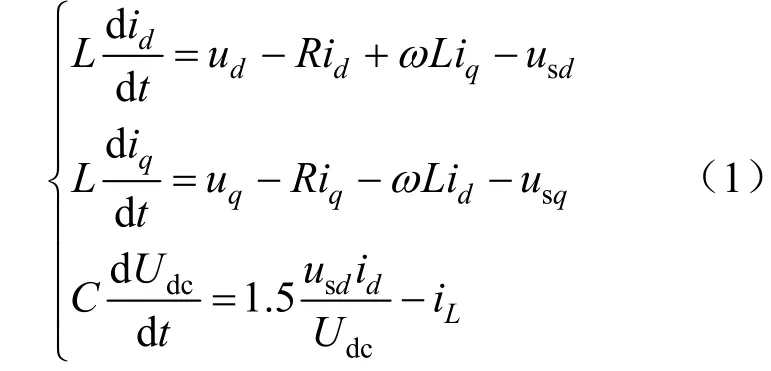
式中：Ud=UdcSd，Uq=UdcSq；Sd、Sq分別為開關函數的d、q軸分量；usd、usq分別為電網電壓在d、q軸上的分量；id、iq分別為逆變器交流側電流在d、q軸上的分量；iL為流入逆變器的電流。

2 滑模控制器設計

滑模控制器的設計包括3個部分。

（1）設計滑模面：使系統運動點在滑模面上保持良好的動態特性。

（2）設計趨近律：決定了系統運動點趨向滑模面過程中的動態特性及逼近切換面時的抖振程度。

（3）設計控制率：滿足滑模控制器的控制目標，使系統能從任意初始狀態在有限時間內到達滑模面。

為實現并網控制目標，本文采用如圖2所示雙閉環滑模控制策略。

圖2 并網逆變器控制框圖 Fig. 2 Control block diagram of the grid-connected inverter

圖2中，直流側電壓Udc與參考電壓比較后，經電壓外環計算得到電流內環d軸參考值； 內環滑模控制器的計算結果經反Park變換得到控制信號uα、uβ。

考慮到外界不確定干擾對系統的影響，式（1）可改寫為：

式中：d1、d2項表示由系統參數攝動、負載變化引起的如電網電壓波動等不確定擾動；Cd3項表示由電容容差、光照強度變化等引起的逆變器直流側不確定擾動。

2.1 電壓外環控制器設計

根據系統的控制目標，定義電壓外環控制器的跟蹤誤差為：

跟蹤誤差的導數為：

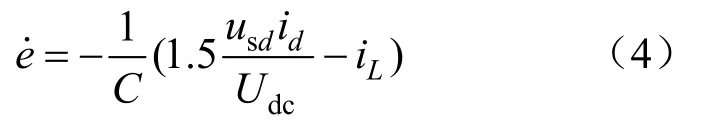
為了減少系統穩態誤差，補償系統的不確定性，引入積分滑模面：

采用指數趨近律，令

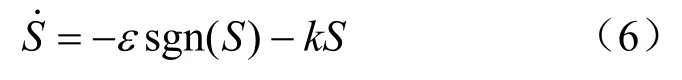
將式（5）與式（4）（6）聯立得電壓外環滑模控制率為：

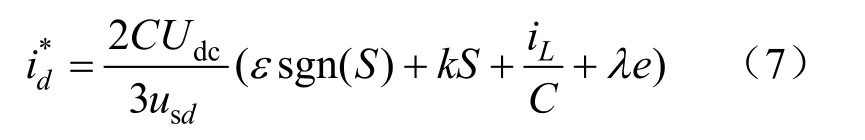
式中：ε＞|d3|；k＞0；kS為指數趨近項，λe為比例項，兩者共同保證了當系統運動點離切換面較遠時，能以較大的速度趨近切換面；εsgn(S)為等速趨近項，保證了系統運動點在有限時間到達切換面；iL/C為受系統參數影響的控制項。

結合式（2）（7）可以證明

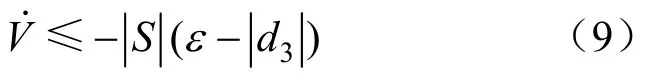
由式（9）可以看到，在ε＞|d3|、k＞0的條件下，本文所設計的電壓外環滑模控制器在滿足滑模穩定性條件的同時，可保證系統的魯棒性。

2.2 電流內環控制器設計

根據系統的控制目標，選取逆變器輸出電流為控制量，定義電流內環控制器的跟蹤誤差為：

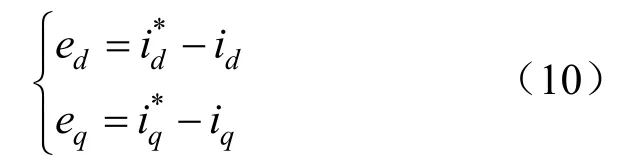
為了實現單位功率因數并網，需對無功電流iq進行控制，即式（10）中=0。

電流內環的滑模面采用：

式中：c1、c2表示控制器跟蹤誤差的收斂速度。在該滑模面下，跟蹤誤差將指數收斂于0。

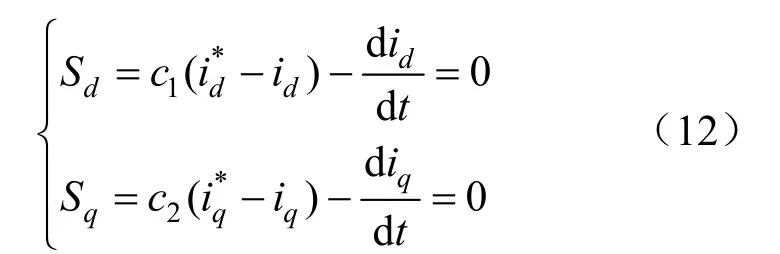
將式（1）與式（12）聯立得：

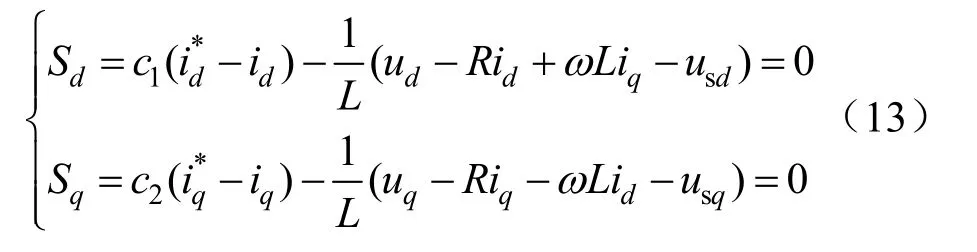
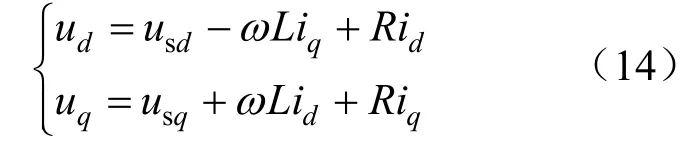
將式（13）（14）聯立可以得到簡化后的滑模面：

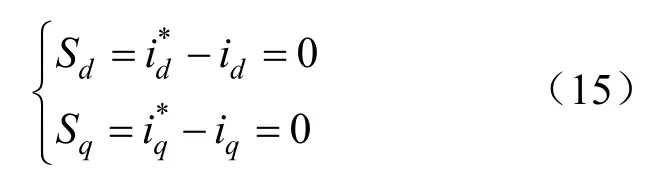
目前，常用的趨近律有等速趨近律、指數趨近律、冪次趨近律等。等速趨近律的趨近速度與抖振程度取決于單一系數；指數趨近律在其基礎上增加了指數項以提高趨近速度，但當S接近零時趨近速度仍較大。

為降低抖振，在系統狀態趨近于滑動模態（S較小）時，需要確保控制增益較小。若進一步考慮應用冪次趨近律，則由于不存在指數項，趨近過程會較為緩慢。

本文采用一種新型的趨近律：

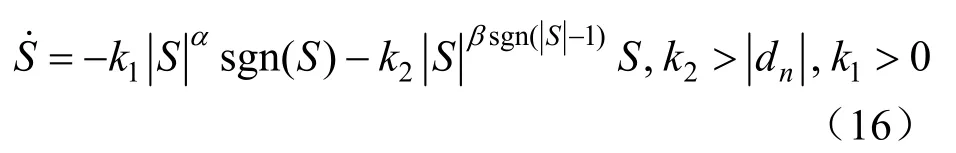
式中：n=1,2；α、β為正的控制參數。

在本文所設計的系統中，α、β為恒定值。經仿真，此處α取值為0.5，β取值為2。

當系統狀態遠離切換面（|S|＞1）時，由于控制參數β的存在，趨近律的第二項等效為指數項，可以保證該趨近律的趨近速度高于冪次趨近律。此時，k2決定了系統狀態向切換面的趨近速度。

當系統狀態接近切換面（|S|＜1）時，該趨近律可以保證較小的控制增益，以降低抖振。此時，k1決定了系統狀態到達切換面的趨近速度和抖振程度。為了保證快速趨近的同時削弱抖振，應在增大k2的同時減小k1。

聯立式（1）（15）（16），得到改進后的電流環滑模控制率為：

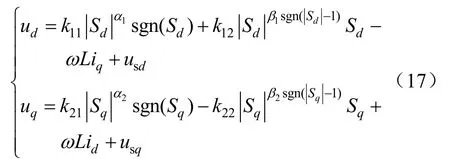
式中：常數k12、k22為指數趨近項系數。

k12、k22越大，系統狀態距切換面較遠時到達速度越快；k11、k21越大，系統狀態接近切換面時的趨近速度越快；但該值的增大也將引起系統的抖振程度的增加。

在該控制律中，為了保證系統狀態快速趨近切換面的同時削弱抖振，應在增大k12、k22的同時減小k11、k21。

以電流環滑模控制率的d軸分量為例進行穩 定性分析，定義Lyapunov函數，則

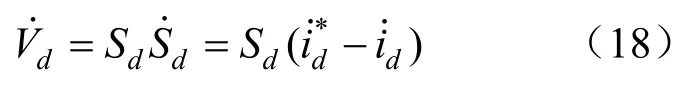
結合式（2）（17）可以證明

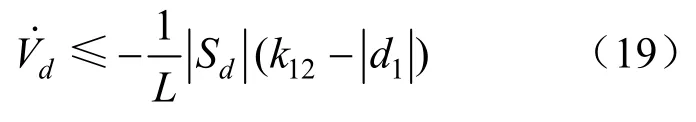
由式（19）可以看到，在k12＞|dn|、k22＞|dn|、k11＞0、k21＞0條件下，本文所設計的電流內環滑模控制器滿足滑模穩定性條件，同時可保證系統的魯棒性。

3 仿真及結果分析

為了驗證所設計滑模控制器的有效性，依據圖2在MATLAB/Simulink中搭建仿真模型。

在理想電網條件下，分別采用雙閉環PI控制和雙閉環滑模控制進行對比仿真研究。

系統的主要參數見表1。

表1 系統仿真參數 Tab. 1 System simulation parameters

3.1 動態性能和穩態性能分析

分別對比在2種控制方式下的A相入網電流及電壓波形、直流側電壓波形、入網電流總諧波畸變率，分析系統響應的動態與穩態性能。

3.1.1 入網電流及電壓分析

A相入網電流及電壓波形對比結果分別如圖3、圖4所示。

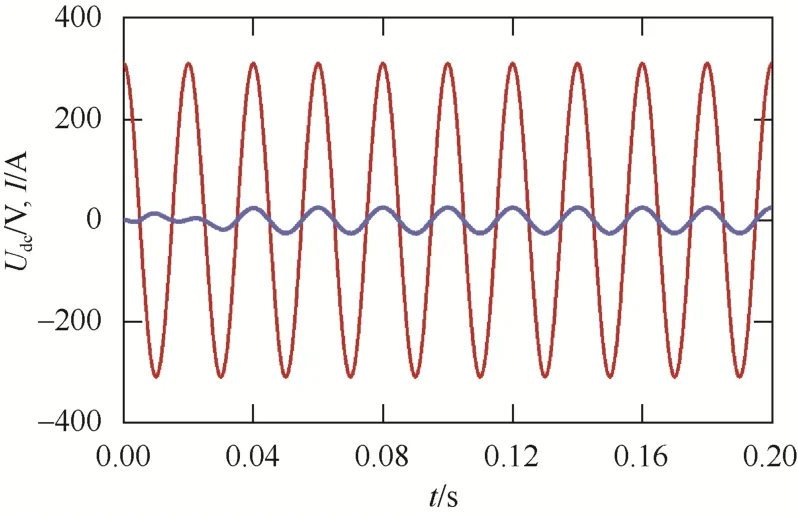
圖3 滑模控制下的A相入網電流及電壓波形 Fig. 3 Waveform of A-phase grid connected current and voltage under sliding mode control

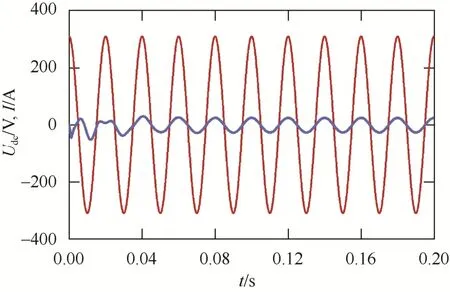
圖4 PI控制下的A相入網電流及電壓波形 Fig. 4 Waveform of A-phase grid connected current and voltage under PI control

由圖3、圖4可知，對于入網電流，PI控制下達到穩態值的時間約為0.06 s，而滑模控制下達到穩態值的時間約為0.03 s；在調節時間內，PI控制下的入網電流振蕩幅度明顯大于滑模控制。

3.1.2 直流側電壓分析

直流側電壓波形對比結果如圖5所示，動態性能對比結果如表2所示。

圖5 光伏并網逆變器的直流側電壓對比 Fig. 5 Comparison curve of the DC side voltage of PV grid-connected inverter

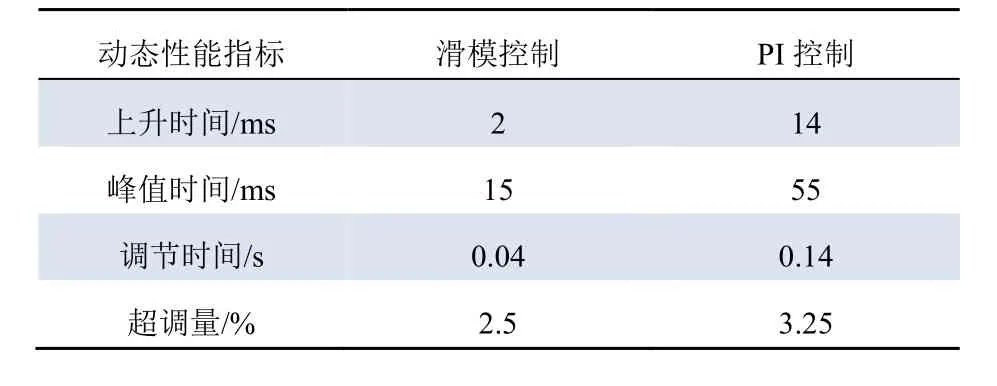
表2 直流側電壓的動態性能對比 Tab. 2 Comparison of dynamic property of the DC side voltage

由圖5及表2可知，對于逆變器直流側電壓，在滑模控制下，上升時間、峰值時間及調節時間遠小于PI控制，證明所設計滑模控制器響應的總體快速性優于PI控制；在滑模控制下的超調量小于PI控制，證明所設計滑模控制器響應的平穩性優于PI控制。

3.1.3 入網電流總諧波畸變率分析

A相入網電流的總諧波畸變率（total harmonic distortion，THD）對比結果如圖6、圖7所示。

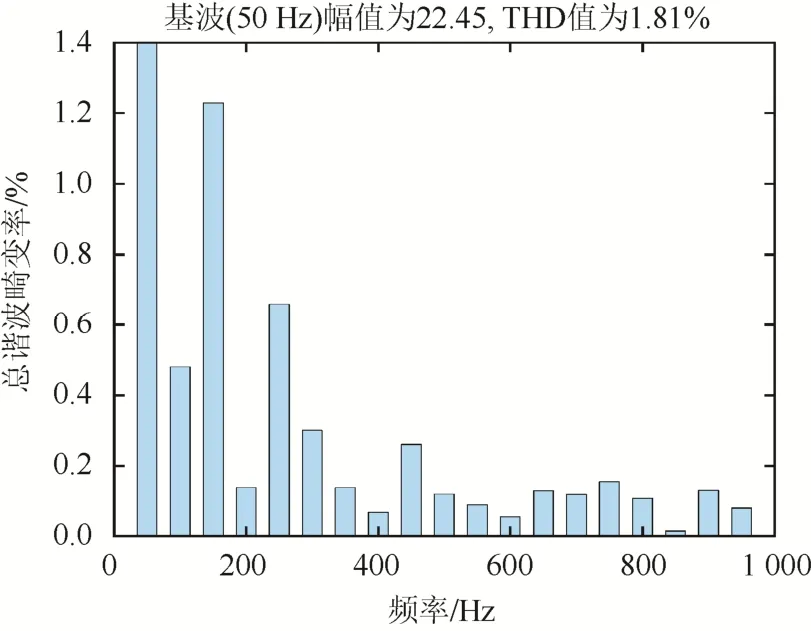
圖6 A相入網電流在滑模控制下的總諧波畸變率 Fig. 6 Distortion rate of A-phase grid connected current under sliding mode control

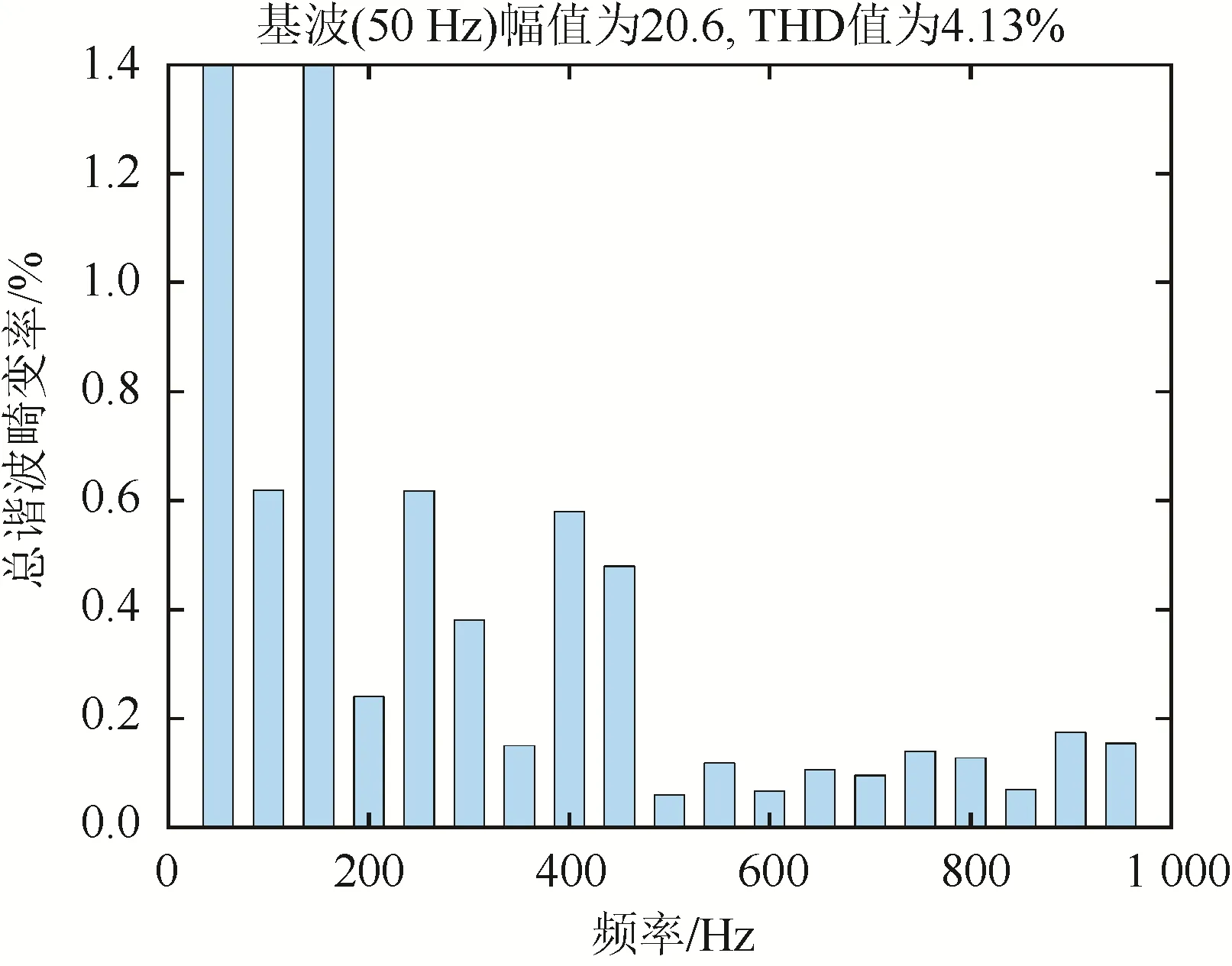
圖7 A相入網電流在PI控制下的總諧波畸變率 Fig. 7 Distortion rate of A-phase grid connected current under PI control

由圖6、圖7可知，滑模控制下的THD為1.81%，PI控制下的THD為4.13%，兩者都滿足“小于5%”的并網標準；但滑模控制下的電流總諧波畸變率顯著低于PI控制。

3.2 魯棒性能分析

3.2.1 光照強度變化對系統的影響

為了分析直流側不確定擾動Cd3對系統的影響，以光照強度的變化作為逆變器直流側不確定擾動的因素，進行仿真計算。

光伏陣列的工作環境設置為：溫度25 ℃，光照強度1 kW/m2，從0.5 s變為500 W/m2。

圖8為該環境下，采用這2種控制方式時的直流側電壓波形對比。

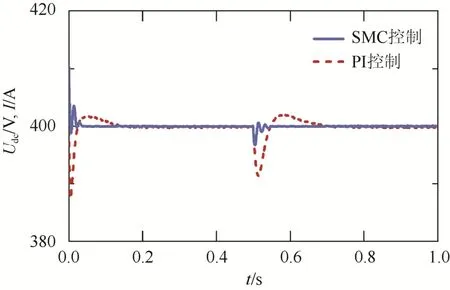
圖8 光照強度變化時的直流側電壓對比 Fig. 8 Comparison curve of the DC side voltage under light intensity changes

由圖8可見，0.5 s到1 s期間，由于光照強度的突變，2種控制方式下逆變器直流側電壓出現了不同程度的跌落：在滑模控制下，系統恢復穩態的時間約為0.06 s，期間電壓最大跌落值約5 V；PI控制下系統恢復穩態的時間約為0.2 s，期間電壓跌落最大值約10 V。可見，對于直流側電壓的擾動，所設計的滑模控制器表現出較強的魯棒性。

3.2.2 電網電壓波動對系統的影響

為了分析不確定擾動d1、d2對系統的影響，用電網電壓波動模擬系統參數攝動、負載變化等引起的網側電壓波動，開展仿真實驗。

仿真實驗參數設置為：系統電網電壓有效值為220 V，峰值約為311 V，允許偏差為±10%。電網電壓在0.4 s時降低10%，在0.6 s時恢復到311 V。

電網電壓波動時，2種控制方式下的直流側電壓波形對比結果如圖9所示，系統頻率對比結果如圖10所示。

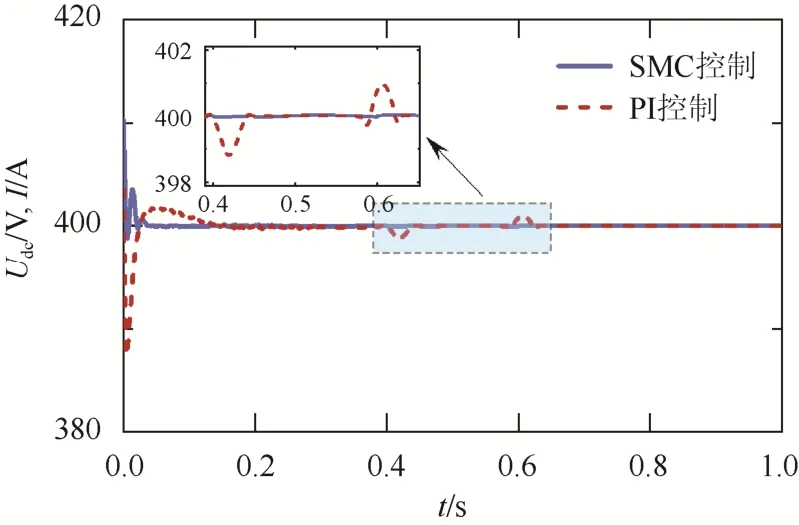
圖9 電網電壓波動下的逆變器直流側電壓 Fig. 9 The DC side voltage of PV grid-connected inverter under grid voltage fluctuation

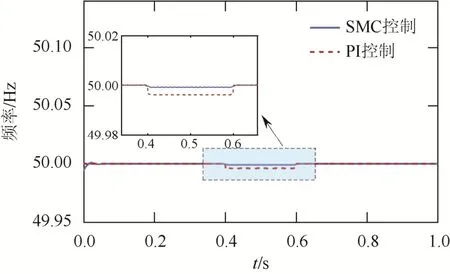
圖10 電網電壓波動下的系統頻率 Fig. 10 System frequency under grid voltage fluctuation

由圖9可以看出：在0.4 s電網電壓降低時，逆變器直流側電壓在滑模控制下幾乎無波動；在PI控制下，直流側電壓存在約2 V的跌落，約0.03 s后恢復到穩態。在0.6 s電網電壓恢復時，滑模控制下的逆變器直流側電壓幾乎無波動；在PI控制下，直流側電壓升高約2 V，約0.03 s后恢復到穩態。

由圖10可見，發生電網電壓波動時，在2種控制方式下，系統頻率都出現了微小的降低；滑模控制下的系統頻率降低幅度顯著低于PI控制。

綜上可知，在網側電壓出現不確定干擾時，所設計的滑模控制器表現出較強的魯棒性。

4 結論

考慮光伏并網系統存在直流側和網側不確定干擾，本文提出了一種改進的雙閉環滑模控制策略。通過仿真實驗，將本文策略與傳統的逆變器控制策略進行對比分析，得出的主要結論如下。

（1）本文控制策略通過電流內環滑模控制，實現了對入網電流的反饋控制、入網電流的正弦化及單位功率因數并網，通過電壓外環滑模控制實現了直流側電壓穩定。對趨近律和滑模面的改進以及積分環節的引入，有效提高了系統的動穩態性能。

（2）針對外界不確定干擾問題，在電流內環滑模控制器中引入了新型趨近律，通過其在系統狀態遠離切換面條件下所具有的高增益特性，削弱了系統抖振，使系統獲得較好的魯棒性、表現出良好的抗干擾能力。