基于汽輪機相對內效率分析的低壓缸 效率計算

馮垚飛，馮林魁，谷志德，趙 凱，王 平

（國網甘肅電力公司電力科學研究院，甘肅 蘭州 730070）

0 引言

汽輪機缸效率是反映機組運行以及做功狀態的一項重要經濟性指標。大型機組的高、中壓缸進出口蒸汽均為過熱蒸汽，缸效率只與進出口蒸汽壓力、溫度有關；低壓缸出口蒸汽為濕蒸汽，缸效率不僅與進出口壓力、溫度有關，還與排汽濕度有關。

由于目前還沒有準確有效的蒸汽濕度測量手段，所以低壓缸效率也是大型機組經濟性計算的難點之一。根據行業性能試驗標準，在考慮排汽損失前提下計算低壓缸效率時，需要通過反復迭代外推計算至低壓缸膨脹線終點焓收斂。這種方法在計算時需要對系統進行嚴格隔離；而且由于末幾級同為濕蒸汽，抽汽焓也要通過迭代的方式計算，所以計算量較大且過程復雜。

相關文獻中，關于低壓缸效率計算方法的研究很多，最常見的有弗留格爾公式法、熵增法、神經網絡法、焓降法等。文獻[1]提出用基于免疫原理的多層徑向基函數（RBF）神經網絡數學模型來計算汽輪機的低壓缸相對內效率。文獻[2]給出了一種末級流態的判斷方法。文獻[3]將低壓缸、凝汽器以及與低壓缸抽汽相對應的回熱加熱器視為一開口熱力系統，根據該開口系統的能量平衡提出了一種在線計算排汽焓和低壓缸效率計算方法。文獻[4]根據弗留格爾公式提出了一種實時計算缸效率的模型。文獻[5]將一種改進的迭代算法應用于低壓缸效率的計算，并分析了常規方法測量雙背壓低壓缸效率的誤差。文獻[6]采用變工況計算方法對各缸的能耗敏感性進行了定量分析。文獻[7]將免疫小波方法引入低壓缸排汽焓的計算中。文獻[8]研究了汽輪機缸效率對機組經濟性的影響。文獻[9]通過變背壓試驗找出了低壓缸相對內效率最佳值。上述方法在使用時需要構建復雜的數學模型，所以在實際應用中具有一定的局限性；其中一些方法在計算參數時因采用近似值，從而導致其計算精度下降，誤差范圍較大。

本文以汽輪機常規性能試驗為基礎，提出了一種低壓缸效率計算方法：假設蒸汽在汽輪機內進行等熵膨脹做功；根據各缸的等熵膨脹線與回熱抽汽的交點計算得出等熵狀態下的回熱抽汽焓；利用等熵狀態下質量、能量平衡方程計算加熱器等熵抽汽量以及汽輪機等熵排汽量，并將軸封漏汽損失修正至等熵狀態；根據熱量平衡計算蒸汽等熵膨脹做功所消耗的熱量，進而求得汽輪機整體相對內效率；通過汽輪機整體相對內效率與高、中、低壓缸之間的等效關系間接計算低壓缸效率。對于含有多級濕蒸汽抽汽機組，該算法簡化了低壓缸效率計算過程。

1 相對內效率的計算方法

理想狀態下，蒸汽在汽輪機內進行等熵膨脹做功，不參與外部熱量交換。實際做功時，工質需要吸收汽輪機內部摩擦、汽流擾動等損耗而轉變的熱量[10]。這些熱量的存在，使得蒸汽的熵與焓均呈現增加的趨勢；所以蒸汽實際膨脹做功量小于等熵膨脹做功量。圖1示出了等熵狀態與實際狀態下的蒸汽膨脹變化過程。

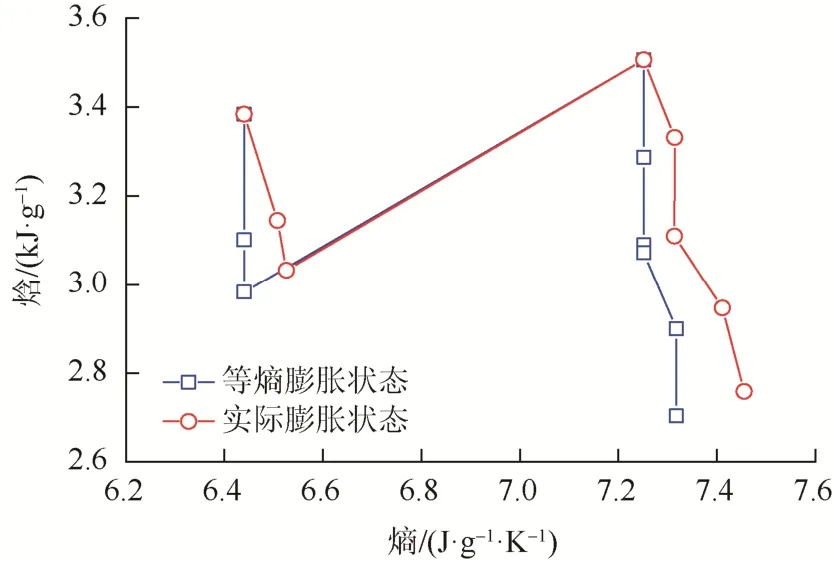
圖1 汽輪機膨脹做功焓-熵圖 Fig. 1 Enthalpy-entropy diagram of steam turbine expansion

汽輪機整體相對內效率的定義為汽輪機實際功率與理想功率的比值。理想功率是蒸汽進入汽輪機做等熵膨脹時所做的功。根據汽輪機能量平衡關系，理想功率與蒸汽等熵膨脹過程中的循環熱量之間的關系可表示為：

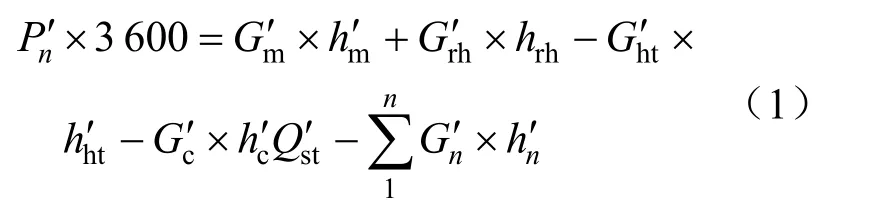
式中：nP′為機組等熵膨脹下的理想內功率；G、h分別表示等熵狀態時工質的流量和焓值；下標m、ht、rh、c分別代表主蒸汽、高壓缸排汽、再熱蒸 汽、低壓缸排汽；n代表回熱抽汽總級數；stQ′為 等熵狀態下機組漏汽損失。

機組的實際內功率與發電機功率之間的關系為：

式中：Pn為機組實際內功率；Pi為發電機功率；mη為機械損失；gη為電氣損失。

汽輪機整體相對內效率為：

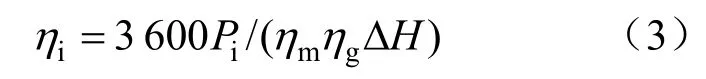
1.1 等熵膨脹狀態下回熱抽汽流量計算

首先，求出高、中、低壓缸的等熵膨脹線。根據實測各級回熱抽汽點的抽汽壓力與等熵膨脹線的交點，確定各回熱抽汽點的等熵膨脹焓。對于末級濕蒸汽，其等熵膨脹焓只與抽汽壓力和低壓缸進汽熵有關。保持主給水流量不變，根據高壓加熱器及除氧器熱量平衡計算等熵膨脹狀態下各段抽汽流量。

由于等熵狀態下的抽汽焓發生變化，高壓加熱器、除氧器回熱抽汽量及疏水量也會發生變化。根據流量平衡計算除氧器進口主凝結水流量；以主凝結水流量為基準，根據低壓加熱器流量和熱量平衡，確定等熵膨脹狀態下低壓加熱器回熱抽汽流量。

1.2 小機進汽及軸封漏汽量的修正

小機進汽流量和軸封漏汽流量均是在實際膨脹過程中測量得到的；計算時需要將其修正至等熵膨脹狀態，修正計算公式為：

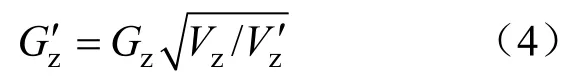
式中：zG′為等熵膨脹狀態下蒸汽流量；Gz為實際膨脹狀態下蒸汽流量；zV′為等熵膨脹狀態下蒸汽 比容；Vz為實際膨脹狀態下蒸汽比容。

對于汽動給水泵機組，需要將小機進汽流量和軸封漏汽流量修正至等熵狀態；對于電動給水泵機組，只需對軸封漏汽流量進行修正即可。

1.3 等熵膨脹狀態下各缸進、排汽流量及排汽焓

進入機組的主蒸汽流量為：

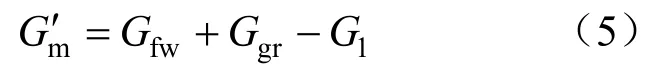
式中：G1為機組不明泄漏量，可以根據除氧器、熱井水位的漲落進行計算。

等熵狀態下，機組的給水流量及減溫水流量不會發生變化，因此等熵膨脹狀態與實際膨脹狀態下的主蒸汽流量相等。

等熵膨脹狀態下的高排流量、再熱蒸汽流量以及低壓缸排汽流量均可通過蒸汽流量平衡計算推導得出：

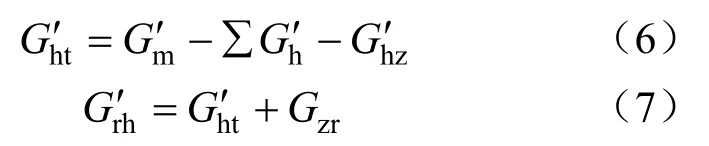
式中：G′ht、G′rh分別為等熵膨脹狀態下的高排流量、再熱蒸汽流量；hG′為高壓缸對應的回熱抽汽流量。例如，高壓缸下有2級回熱抽汽，∑G′h即為2級回熱抽汽流量之和。G′hz為高壓缸軸封漏汽 流量，需要通過式（8）修正至等熵膨脹狀態。

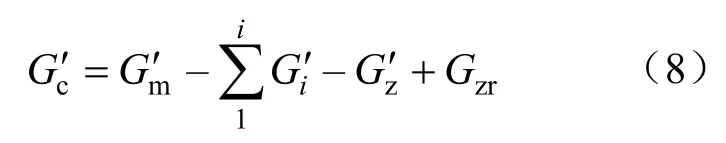
式中：G′c為等熵狀態下低壓缸排汽流量；G′i為等 熵狀態下加熱器抽汽流量；i為加熱器個數。

等熵狀態下的低壓缸排汽焓可以根據凝汽器壓力和低壓缸進汽等熵線的交點計算得出。

將等熵膨脹狀態下計算得到流量與焓值代入式（3）可以計算出實際運行工況下機組整體相對內效率。

2 相對內效率與缸效率的關系

機組整體相對內效率與高、中、低壓缸效率之間的關系可表述為[11]：

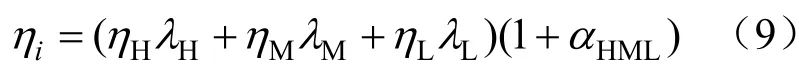
式中：αHML為機組重熱系數；ηH、ηM、ηL分別為高壓缸、中壓缸及低壓缸效率；λH、λM、λL分別為高壓缸、中壓缸及低壓缸等熵焓降占整機等熵焓降的比重，即

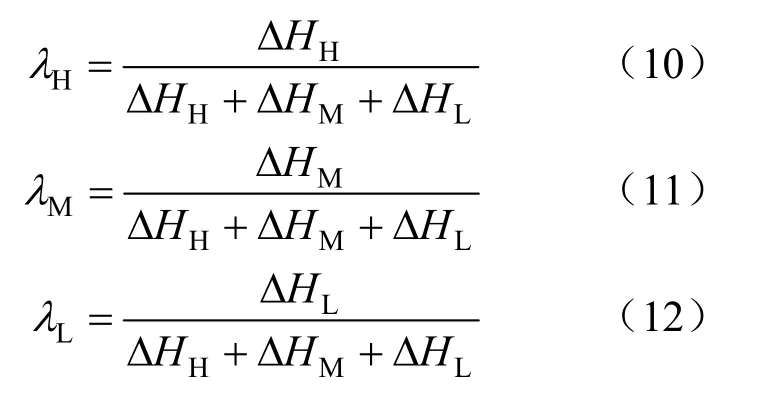
多級汽輪機中，前級損失使得后級等熵焓降增加，即前級的損失在后級仍能得到利用。這種現象稱為汽輪機重熱現象。重熱系數是量化該現象的參數，其定義為：

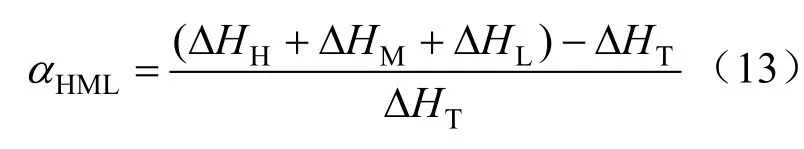
式中：ΔHH、ΔHM、ΔHL、ΔHT為高壓缸、中 壓缸、低壓缸及汽輪機整機等熵焓降，其值為進口焓與出口等熵排汽焓的差值。

通過機組整體相對內效率與低壓缸效率之間的等效關系可以間接地計算出實際運行工況下真實的低壓缸效率。

3 計算實例

分別選取不同容量機組進行試驗。試驗機組容量分別為660 MW、330 MW、300 MW，試驗機組的設計參數如表1所示。

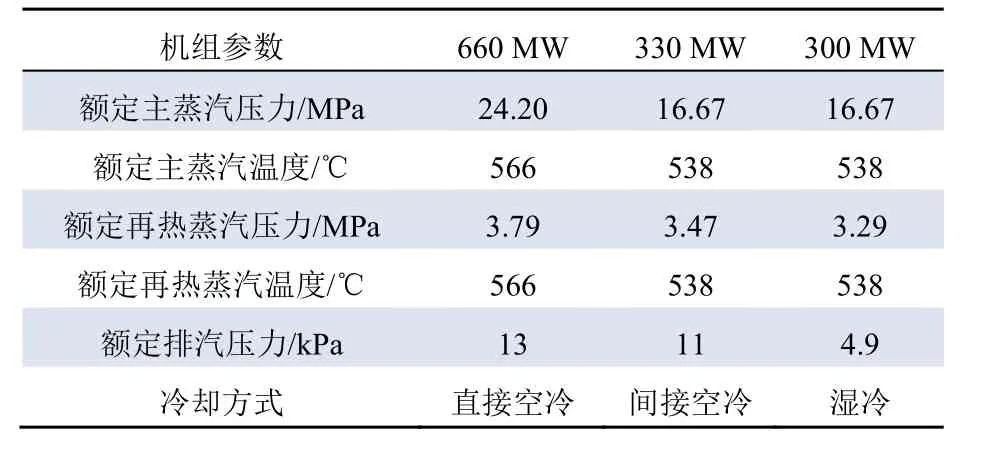
表1 不同容量機組設計參數 Tab. 1 Design parameters of turbine units with different capacities

等熵狀態下，機組用于做功的熱量增加，輸出功率也相應地增加。為了驗證算法的精度，將本文方法熱耗率驗收工況計算結果與ASME標準計算方法進行對比，結果如表2所示。

從表2所示的計算結果可以看出，與ASME標準下的低壓缸排汽焓計算值相對比，根據本文方法所得的低壓缸排汽焓最大計算誤差為3.92 J/g。誤差產生的主要原因是：計算時，各缸的軸封漏汽修正至等熵狀態下疊加產生的修正誤差。本文算法的計算精度完全滿足工程要求。

4 結論

針對汽輪機組相對內效率，給出了間接計算低壓缸效率的算法，避免了復雜的膨脹線迭代分析。

分別以660 MW、330 MW、300 MW機組為例，通過汽輪機熱力性能試驗計算分析了變工況運行下的低壓缸效率，并與常規ASME標準計算結果進行了對比。結果顯示，低壓缸排汽焓最大計算誤差為3.92 J/g，精度滿足工程要求。