軟質聚氨酯泡沫的動態(tài)壓縮力學性能和本構模型*

蘇興亞，周 倫,2，敬 霖，鄧貴德，趙隆茂

（1. 西南交通大學牽引動力國家重點實驗室，四川 成都 610031；2. 四川航空工業(yè)川西機器有限責任公司，四川 雅安 625000；3. 中國特種設備檢測研究院，北京 100029；4. 太原理工大學應用力學研究所，山西 太原 030024）

聚氨酯泡沫（polyurethane foam, PUF）作為一種高孔隙率的多功能材料，具有易于加工、高比強度、良好的能量吸收和緩沖隔振性能，被廣泛應用于汽車工業(yè)、軌道交通、航空航天和包裝工程等領域。根據其胞孔構型的不同，可分為閉孔型硬質聚氨酯泡沫（rigid polyurethane foam, RPUF）和開孔型軟質聚氨酯泡沫（flexible polyurethane foam, FPUF）。PUF 作為民用工程防護材料時，服役過程中可能遭受的動態(tài)沖擊作用情形如汽車碰撞、物體墜落等，通常為中應變率動態(tài)載荷。因此，研究中低應變率下PUF 壓縮力學性能和本構關系，具有重要的學術和工程價值。

目前，針對聚氨酯泡沫的研究多聚焦于RPUF，且主要集中在準靜態(tài)和高應變率加載情形。學者們開展了不同密度RPUF 的壓縮力學性能實驗，發(fā)現其靜動態(tài)應力-應變曲線均表現出泡沫材料典型的三階段特征，從細觀層面揭示了不同壓縮階段胞孔的變形行為，并對其能量吸收特性進行了評估。結果表明，RPUF 具有一定的應變率敏感性和密度依賴性，其屈服應力和平臺應力隨應變率和密度的增加而增大，且高密度RPUF 的應變率敏感性更加明顯。此外，準靜態(tài)加載下RPUF 的能量吸收效率隨密度的增加而減小，而高應變率加載下兩者沒有明顯的關聯性。在本構模型方面，一些學者基于黏彈性和黏彈塑性材料假設，提出了一系列可描述PUF 壓縮力學響應的本構模型，并給出了材料的屈服準則，但是這些模型的參數較多且計算復雜，不便于工程應用。近年來，基于實驗數據擬合的經驗型和半經驗型本構模型因具有使用方便、物理意義明確等優(yōu)點被廣泛發(fā)展和使用，如Rusch 模型、Sherwood-Frost (S-F)模型和Avalle 模型等。然而，對于中低應變率下FPUF 壓縮力學性能和本構關系的研究還比較匱乏，其應變率敏感性和能量吸收特性還不夠明確。

本文中，擬開展FPUF 的中低應變率壓縮力學性能實驗，分析其力學響應特征和應變率敏感性，并對其能量吸收特性進行評估；基于靜動態(tài)壓縮實驗結果，通過引入應變率相關參數，構建可描述FPUF 應力-應變響應特征的修正S-F 模型和修正Avalle 模型。

1 實 驗

實驗選用由發(fā)泡工藝制成的開孔型FPUF，密度為0.176 g/cm，試件邊長為50 mm，高為25 mm，如圖1(a)所示。圖1(b)給出了FPUF 的細觀結構圖，其中胞孔呈圓形或橢圓形且均勻性良好，胞孔之間通過胞壁孔隙實現相互連通，其平均孔徑為0.35 mm，材料的平均孔隙率為0.84。采用DDL-200 電子萬能試驗機開展了應變率為0.001 和0.01 s時FPUF 的準靜態(tài)壓縮力學性能實驗，壓縮應變均大于80%。采用Instron 9350 落錘試驗機開展40、70 和100 s等3 種應變率下FPUF 的動態(tài)壓縮力學性能實驗。落錘總質量為9.993 kg，選取直徑為100 mm 的鋼質圓形錘頭。實驗時錘頭分別在0.051、0.156 和0.919 m 高度自由下落以實現3 種應變率加載，對應的沖擊能量分別為4.997、15.302 和31.228 J，錘頭定位精度為±1 mm。圖2 給出了準靜態(tài)和動態(tài)壓縮實驗裝置及相關實驗細節(jié)。為了保證實驗結果的可靠性，每種應變率下均開展3 次有效重復性實驗，選擇最接近平均值的應力-應變響應曲線進行應變率敏感性和能量吸收特性分析。

圖1 FPUF 試件尺寸和SEM 圖像Fig. 1 The specimen size of FPUF and its SEM image

圖2 準靜態(tài)和動態(tài)壓縮實驗裝置Fig. 2 Equipment for quasi-static and dynamic compression experiments

2 實驗結果與討論

2.1 應力-應變響應

圖3 為FPUF 的靜動態(tài)壓縮應力-應變曲線，可以看出，相同應變率下3 次實驗的應力-應變曲線重復性較好，說明實驗結果具有較高的可信度。不同應變率下材料均表現出三階段（彈性段、平臺段和密實化段）變形特征，其壓縮應力隨應變的增大逐漸提高。這是因為：在壓縮變形初期，沿加載方向較大的胞孔首先發(fā)生彈性擠壓變形，此時應力隨應變的增大呈線性提高；當試件繼續(xù)被壓縮時，已變形胞孔周圍的胞壁也逐漸發(fā)生彎曲和扭轉，導致該胞孔變形加劇并在其附近形成坍塌區(qū)，材料由彈性段逐漸進入到平臺段，而坍塌區(qū)數量隨試件壓縮變形量的增加不斷增加，宏觀上表現為平臺段應力隨應變的增大緩慢提高；隨著試件壓縮變形加劇，大量胞壁之間產生接觸并不斷相互擠壓導致應力迅速增大，材料逐漸進入到密實化段。對比發(fā)現，準靜態(tài)加載下應力-應變曲線中的平臺段相對較長，而動態(tài)加載下平臺段隨應變率的升高明顯變短。與RPUF 不同的是，本文中FPUF 在卸載后試樣的壓縮變形幾乎可以完全恢復，而RPUF 則會產生永久變形或破壞。

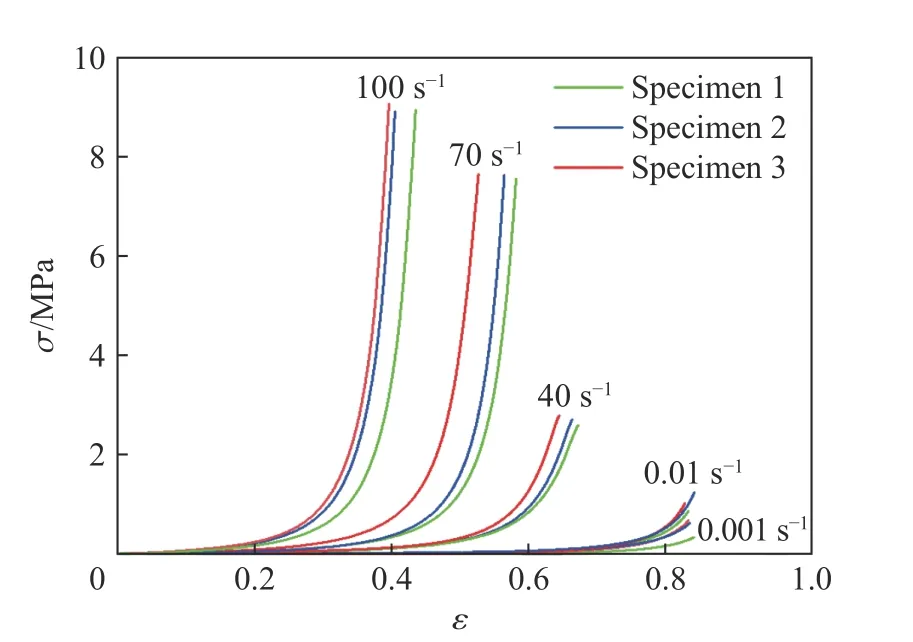
圖3 在不同應變率下FPUF 的壓縮應力-應變關系Fig. 3 Compressive stress-strain curves of FPUF at different strain rates

密實化應變ε是表征泡沫材料壓縮變形能力的重要參量，其確定方法主要有經驗法、切線法和能量吸收效率法。經驗法假設ε與材料的相對密度 ε=-ρˉ 線性相關，其計算方法為 ε=-ρˉ ，其中和為材料參數。切線法認為應力-應變曲線中平臺段切線和密實化段切線交點對應的應變?yōu)槊軐嵒瘧儭Ｄ芰课招史ò炎畲笪苄师菍膽冋J為是密實化應變。經驗法僅適用于準靜態(tài)加載工況，而切線法獲得密實化應變的過程較復雜，因此本文中采用能量吸收效率法計算ε。在任意給定壓縮應變ε下，材料的吸能效率η(ε)為：

式中：σ(ε)為應變ε 對應的應力，σ為應變ε對應的應力。圖4 為應變率為0.001 s時FPUF 典型的吸能效率圖，可知，η(ε)隨工程應變的增大先升高后降低，此時ε的計算方法為：

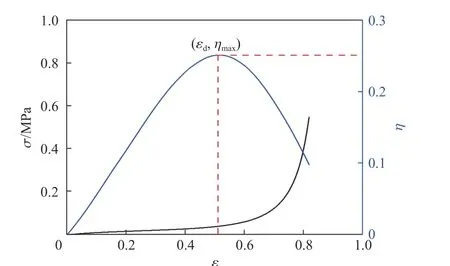
圖4 0.001 s-1 應變率下FPUF 的壓縮應力和吸能效率隨應變的變化Fig. 4 Variation of compressive stress and energy absorption efficiency of FPUF with strain at the strain rate of 0.001 s-1

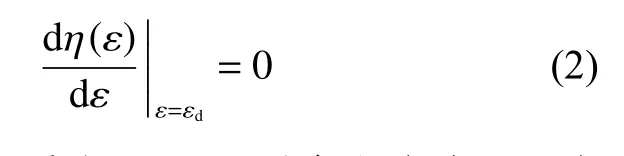
從圖3 可以看出，FPUF 平臺段應力σ隨應變的增大有所提高，很難從應力-應變曲線中直接得到其具體數值。因此，可基于能量吸收原理計算得到：

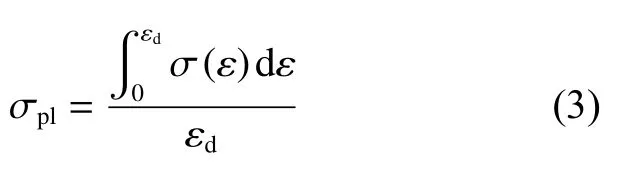
2.2 應變率效應

圖5 為不同應變率下FPUF 密實化應變的計算結果。可以看出，隨著應變率的升高，準靜態(tài)加載下材料的密實化應變相差不大，而動態(tài)加載下其密實化應變顯著減小，高密度PUF和閉孔泡沫鋁也具有相同的特性。不同應變率下FPUF 的平臺應力和屈服應力如圖6 所示，其中平臺應力根據式(3)計算獲得，屈服應力為應力-應變曲線中彈性段切線和平臺段切線交點對應的應力。由圖可知，FPUF 的平臺應力和屈服應力隨應變率的升高而提高，材料表現出應變率強化效應。此外，以鋁（aluminum, Al）、丙烯腈-丁二烯苯乙烯（acrylonitrile butadiene styrene, ABS）、聚乙烯（polyethylene, PE）、聚對苯二甲酸乙二醇酯（polyethylene terephthalate, PET）和聚甲基丙烯酰亞胺（polymethacrylimide, PMI）為基體泡沫材料的平臺應力也出現相同的規(guī)律，如圖7 所示。其中材料的密度（單位：g/cm）已在圖中標注，如FPU (0.176)表示密度為0.176 g/cm的軟質聚氨酯泡沫。對比發(fā)現，相同應變率下FPUF 具有較低的平臺應力，隨著應變率 ε˙ 的升高，不同泡沫材料的應變率敏感性也有所不同。

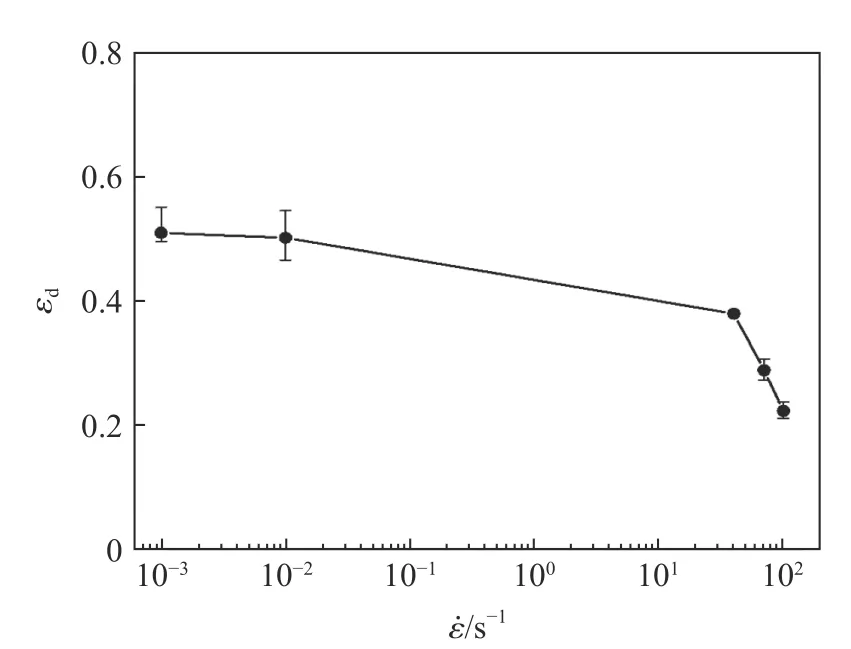
圖5 不同應變率下FPUF 的密實化應變Fig. 5 Densification strain of FPUF at different strain rates

圖6 不同應變率下FPUF 的平臺應力和屈服應力Fig. 6 Plateau stress and yield stress of FPUF at different strain rates

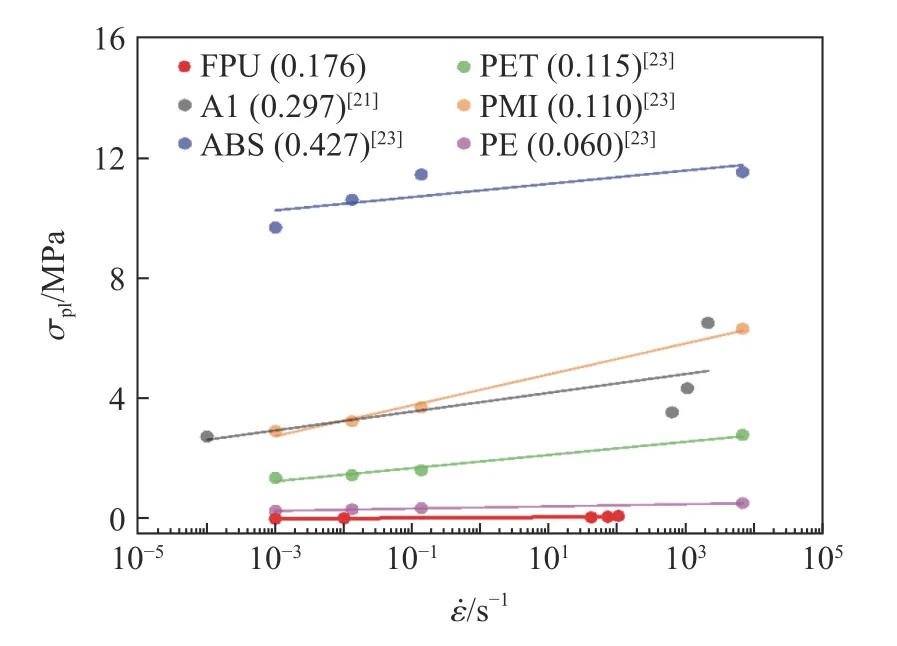
圖7 不同泡沫材料的平臺應力與應變率之間的關系Fig. 7 Relationships between plateau stress and strain rate for different foams

在給定應變下，可用應變率敏感性指數表征泡沫材料塑性應力的應變率敏感程度：

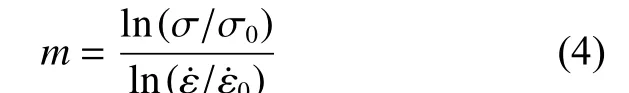
式中： ε˙ 和ε ˙分 別為實驗 應 變 率和參考 應 變 率，σ 和σ分別為對應的應力，本文中參考應變率取0.001 s。圖8 給出了動態(tài)載荷下FPUF 的應變率敏感性指數與應變之間的關系，可以看出，不同工況下均為正值且隨應變率的升高逐漸增大，表明材料具有明顯的應變率強化效應。此外，當應變率為40 和70 s時，在較小應變下FPUF 的應力升高較慢，此時隨應變的增大逐漸減小，當應變達到0.2 時，材料的應力隨應變的增大有較大幅度的提升，從而使得有所增大；當應變率為100 s時，材料的應力隨應變的增大顯著提高，導致隨應變的增大逐漸增大。高分子聚合物泡沫應變率效應產生的主要原因有3 個方面：(1)基體材料的應變率敏感性；(2)胞孔的微慣性效應；(3)胞內氣體的黏性流動。FPUF 的基體為高分子聚合物，是一種應變率敏感性材料，動態(tài)加載下其壓縮力學響應大于準靜態(tài)結果，導致FPUF 表現出應變率強化效應。此外，高應變率下胞孔的微慣性效應會抑制其屈曲變形，使得材料的應力升高。隨著壓縮速率的升高，泡沫材料在塑性變形過程中胞孔內的空氣迅速被壓縮，而壓縮空氣無法在短時間內從胞孔內全部流出，導致氣體的黏性流動阻力增大，該現象在閉孔泡沫材料內更顯著，宏觀上表現為高應變率下材料出現較高的壓縮應力。

圖8 動態(tài)壓縮下FPUF 的應變率敏感性指數與應變之間的關系Fig. 8 Relationship between strain rate sensitivity index of FPUF and strain under dynamic compression

2.3 能量吸收

泡沫材料的壓縮應力-應變曲線中通常存在低應力平臺，導致材料能夠在較低的應力水平下吸收大量能量，當應變?yōu)棣艜r單位體積材料吸收的能量可表示為：

圖9 為不同應變率下單位體積FPUF 吸收的能量隨應變的變化，可以看出，隨應變的增大不斷增大且表現出明顯的應變率強化效應。當泡沫材料壓縮至密實化應變后，其壓縮應力隨應變的增大迅速提高，因此當用于緩沖防護時通常希望材料在密實化應變之前吸收大部分沖擊能量。不同應變率下單位體積FPUF 在密實化應變時吸收的能量如圖10 所示，由圖可知，隨應變率的升高逐漸增大，表明高應變率下FPUF 的能量吸收值更大。

圖9 不同應變率下單位體積FPUF 吸收的能量隨應變的變化Fig. 9 Variation of energy absorbed per unit volume of FPUF with strain at different strain rates

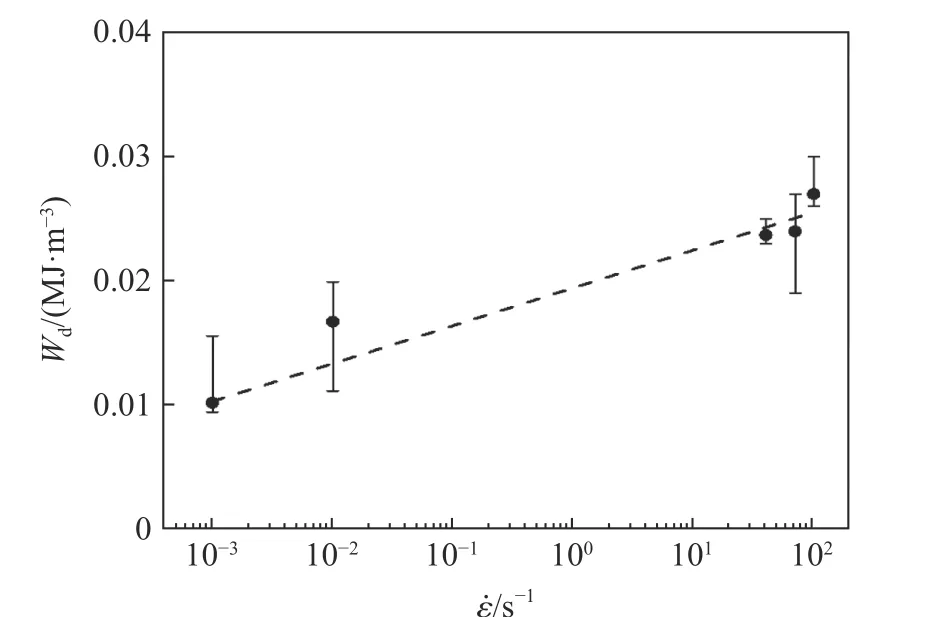
圖10 單位體積FPUF 在密實化應變時吸收的能量隨壓縮應變率的變化Fig. 10 Variation of energy absorbed per unit volume of FPUF at densification strain with compressive strain rates

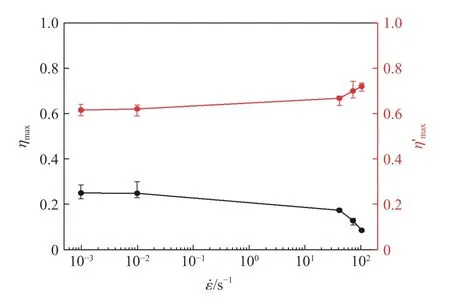
圖11 不同應變率下FPUF 的最大吸能效率和最大理想吸能效率Fig. 11 The maximum energy absorption efficiencies and the maximum ideal energy absorption efficiencies of FPUF at different strain rates

比吸能是評價泡沫材料吸能特性的另一個重要指標，定義為單位質量材料所吸收的能量：

式中：ρ 為材料的密度。

為了研究比吸能隨應變率的變化規(guī)律，本文中選擇應變?yōu)?.4 時材料的比吸能進行分析，如圖12 所示。可以看出，隨著應變率的升高，準靜態(tài)加載下FPUF 的比吸能相差不大，當應變率高于0.01 s時其比吸能顯著提高。此外，圖中還對比了以乙烯-醋酸乙烯聚合物（ethylene-vinyl acetate copolymer, EVA）、發(fā)泡聚乙烯（expanded polyethylene, EPE）、二氧化硅增強聚氨酯（silica reinforced polyurethane, PU/SiO）和陶瓷填充聚氨酯（ceramic filled polyurethane, PU/C）為基體泡沫材料在壓縮應變?yōu)?.4 時的比吸能。可以看出，由于不同材料壓縮力學響應具有不同的應變率敏感性，導致其比吸能隨應變率的變化趨勢有所不同。此外，與圖中其他材料相比，準靜態(tài)加載下FPUF 的比吸能相對較小。當應變率升至100 s時，由于此時FPUF 已進入密實化段，材料所吸收的能量迅速增大，導致其比吸能顯著提高。

圖12 不同泡沫材料的比吸能與應變率的關系Fig. 12 Relationship between specific energy absorption of different foams and strain rate

3 本構模型

泡沫材料通常具有細觀結構多樣、胞孔大小不均等特點，導致從微尺度層面構建其本構模型較復雜，目前研究者主要結合宏觀力學性能實驗來研究其本構關系。其中，以S-F 模型為代表基于實驗結果的經驗型本構模型和以Avalle 模型為代表半經驗型本構模型被廣泛使用。由圖8 可知，FPUF 具有應變率強化效應且應變率敏感性指數受應變和應變率的耦合影響，而S-F 模型中材料的應變率敏感性指數只與應變線性相關，Avalle 模型僅適用于準靜態(tài)加載工況，為了準確描述不同應變率下材料的應力-應變響應，需對模型進行修正。

3.1 Sherwood-Frost 修正模型

為了準確描述率溫耦合下泡沫材料的壓縮力學響應，在Nage 模型的基礎上，通過引入環(huán)境溫度和材料密度相關參量，Sherwood 等提出了考慮多因素影響的S-F 模型，材料的應力σ 為：

式中：、和分別為實驗溫度、參考溫度和環(huán)境溫度；、、、A、和為待定參數。因本文實驗均在室溫下開展且材料密度不變，()和(ρ)均取1。從式(12)可以看出，形狀函數(ε)為應變的級數，且越大擬合精度越高，但同時會增加計算量，因此使用該模型時應充分平衡精度和計算量之間的關系。利用最小二乘法，通過對應變率0.001 s時FPUF 的實驗結果進行擬合，發(fā)現當=8 時便達到很好的預測效果，如圖13 所示，此時形狀函數(ε)的參數值見表1。

表1 形狀函數 f(ε) 的參數Table 1 Fitting parameters of the shape functionf(ε)

圖13 S-F 模型的預測結果和實驗結果的對比Fig. 13 Comparison of the prediction by the S-F model with the experimental result

研究表明，利用式(13) 得到的擬合結果和FPUF 的實驗數據整體上差別較大。為了準確描述靜動態(tài)加載下材料的應力-應變響應，基于壓縮實驗結果，把應變率項修正為：

圖14 對比了模型預測和實驗結果，可以看出，修正后的S-F 模型可以很好地表征不同應變率下FPUF 的壓縮應力-應變響應。

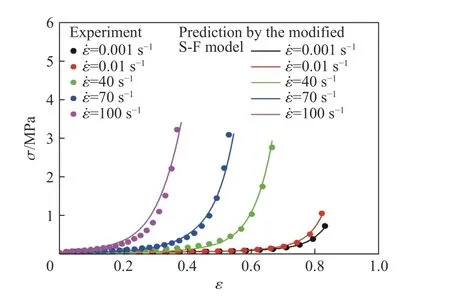
圖14 修正后的S-F 模型的預測結果和實驗結果的對比Fig. 14 Comparison of the predictions by the modified S-F models with the experimental results

3.2 Avalle 修正模型

式中：和分別為材料的彈性模量和平臺應力，、和為應變相關參數。以0.001 s為參考應變率，此時FPUF 的彈性模量和平臺應力分別為0.168 和0.019 6 MPa。利用最小二乘法，對實驗結果進行擬合，得到Avalle 模型的表達式（σ 的單位為MPa）為：

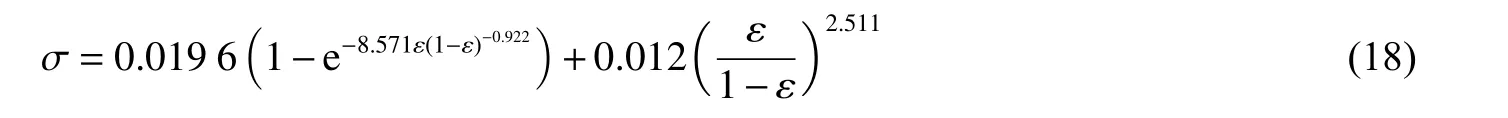
圖15 為準靜態(tài)加載下Avalle 模型的預測結果與實驗結果的對比，可以看出兩者吻合較好，然而該模型沒有考慮應變率的影響。為了準確描述不同應變率下FPUF 的壓縮應力-應變響應，通過在式(18)右側乘以式(14)所示的應變率項對Avalle 模型進行修正，并利用最小二乘法進行數據擬合，得到修正的Avalle 模型（ σ 的單位為MPa）：

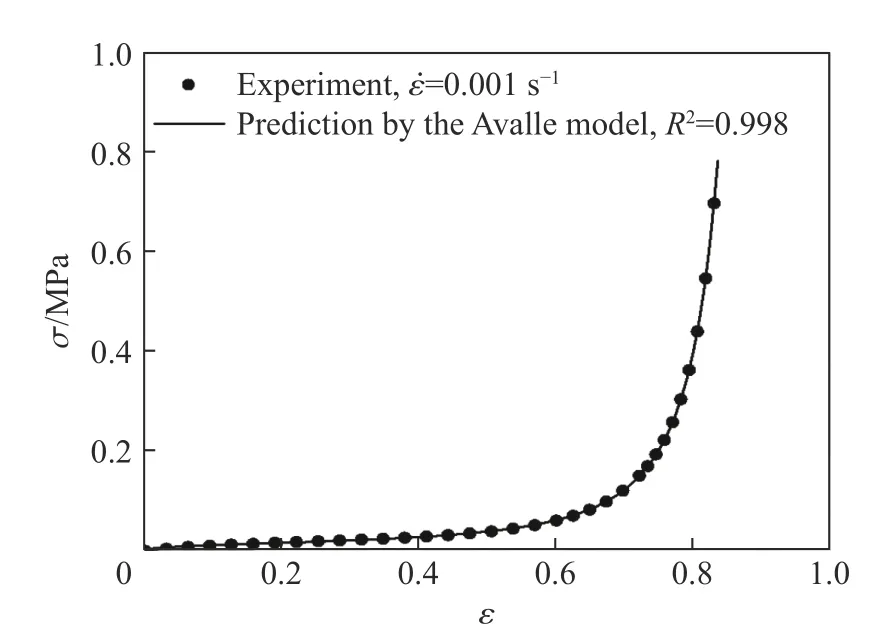
圖15 Avalle 模型的預測結果與實驗結果的對比Fig. 15 Comparison of the prediction by the Avalle model with the experimental result

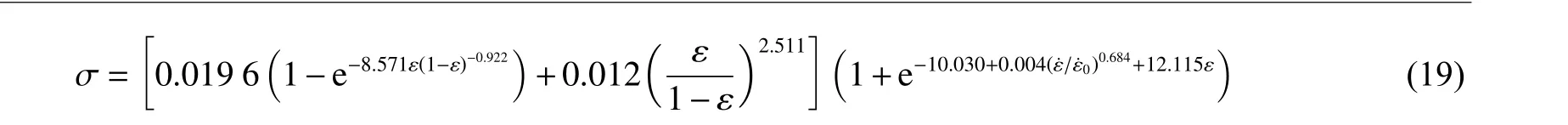
圖16 為修正的Avalle 模型的預測結果與實驗結果的對比，可以看出，修正后的Avalle 模型可以很好地表征應變率對FPUF 應力-應變響應的影響。與修正的S-F 模型相比，修正后的Avalle 模型參數較少且其中和的物理意義明確，便于工程應用。

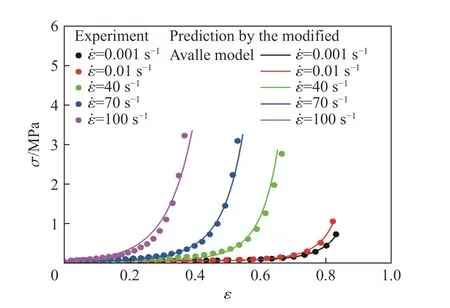
圖16 修正后的Avalle 模型的預測結果與實驗結果的對比Fig. 16 Comparison of the predictions by the modified Avalle model with the experimental results

4 結 論

利用萬能試驗機和落錘試驗機研究了0.001～100 s應變率范圍內軟質聚氨酯泡沫的壓縮力學性能，分析了其應力-應變響應特征和應變率敏感性，討論了應變率對其應變率敏感性指數和能量吸收特性的影響，建立了可準確表征材料靜動態(tài)壓縮力學響應的本構模型，獲得的主要結論如下。

(1)靜動態(tài)加載下，軟質聚氨酯泡沫的應力-應變響應表現出彈性段、平臺段和密實化段的三階段特征，材料具有明顯的應變率強化效應，且應變率敏感性指數受應變率和壓縮應變的耦合影響。

(2)準靜態(tài)加載下，軟質聚氨酯泡沫具有較高的能量吸收效率而能量吸收值較小，應變率對最大吸能效率和比吸能的影響較小；動態(tài)加載下，隨著應變率的升高，最大吸能效率逐漸降低而比吸能明顯升高，應變率為100 s時其比吸能顯著高于其他加載工況。

(3)通過引入應變率相關參量，修正后的S-F 模型和Avalle 模型均能夠很好地表征靜動態(tài)壓縮加載下軟質聚氨酯泡沫的力學響應，但修正后的Avalle 模型的參數較少，更便于工程應用。