金屬材料在復雜應力狀態下的塑性流動特性及本構模型*

秦彩芳，許澤建，竇 旺，杜雨田，黃風雷

（北京理工大學爆炸科學與技術國家重點實驗室，北京 100081）

金屬材料因其優異的力學性能而被廣泛應用于航空航天、交通運輸、能源、國防等重要工業領域，因此研究金屬材料在不同加載條件的力學行為具有重要意義。然而，要在數值模擬中準確預測材料的塑性變形和失效過程，就要對材料的塑性模型及屈服準則提出更高的要求。在塑性本構模型的研究中，研究者多采用與應變率和溫度有關的塑性流動模型，其中包括經驗型以及基于物理意義的模型。近年來，人們發現應力狀態對金屬材料的塑性變形也存在較大影響，因此要在工程計算中獲得精確的結構響應，必須建立考慮應力狀態效應的塑性本構模型。

有關應力狀態對材料塑性的影響目前已有較多研究。Spitzig 等在拉伸和壓縮兩種不同的應力狀態下得到了兩種調質鋼在不同靜水壓力下的應力-應變曲線，發現材料的屈服應力和流動應力均對靜水壓力敏感，表明了材料的力學特性與靜水壓力的相關性。Hu 等認為材料在拉伸和壓縮下的強度差不僅僅是靜水壓力引起的，應力狀態也是導致強度差的主要因素，從而提出了考慮應力狀態影響的各向同性材料屈服準則并用金屬和聚合物材料進行實驗驗證。Cazacu 等發現用應力偏量的主值表示屈服函數可以很好地描述各向異性和拉壓屈服不對稱性材料的塑性行為。Driemeier 等采用光滑和預制缺口的拉伸試樣和剪切試樣，研究了應力強度、應力三軸度和羅德參數對鋁合金材料塑性和失效行為的影響。Brünig 等采用實驗和數值模擬相結合的方法，提出了一種基于應力三軸度和羅德參數的塑性模型和損傷準則，并討論了應力三軸度對韌性金屬損傷起始和演化的影響。Bai 等提出了一種與靜水壓力和羅德角相關的非對稱金屬塑性模型的一般形式，并詳細討論了修正方法，而后通過鋁2024-T351 的實驗結果對新模型的準確性進行了驗證。Gao 等注意到應力狀態對鋁5083 合金的塑性響應和韌性斷裂行為有明顯的影響，提出了與靜水壓力和應力偏量的第三不變量相關的塑性失效模型，并發現應力三軸度主要影響材料的韌性斷裂應變，而羅德角對塑性的影響較大。

目前，考慮材料應力狀態效應的塑性特性及本構模型的研究大多是在準靜態條件下進行的，而在動態加載條件下的相關研究較少。這是因為在高應變率下，材料受到應變率效應和應力狀態效應的耦合作用，難以單獨區分。此外，在進行不同加載條件的力學性能測試時，研究者們采用的試樣類型和尺寸各異，導致實驗結果較為分散，這也給綜合考慮應變率和應力狀態效應的本構模型的建立帶來了困難。針對以上問題，許澤建等提出了一種新型雙剪切試樣，可以在準靜態和動態加載下獲得材料在接近純剪切條件下的流動應力曲線，從而實現了應力狀態效應的解耦。采用該試樣對多種金屬材料在廣泛應變率下的塑性流動、失效行為以及材料的剪切本構特性進行了研究，發現材料的流動應力水平和加工硬化效應明顯受到應力狀態的影響；同時發現剪切本構模型對剪切測試中應力波和流動應力曲線的預測更加精確，因此在工程應用中確定本構模型時必須考慮材料所處的真實應力狀態。

基于以上研究，本文中結合實驗測試提出一個綜合考慮應變率、溫度和應力狀態效應的塑性本構模型，并對其有效性進行驗證，從而實現在復雜應力狀態下準確預測金屬材料和結構的塑性流變及動態響應行為。

1 應力狀態表征

在主應力空間中，與3 個主應力坐標軸夾角相同且過原點的直線稱為等傾線，與等傾線垂直且過原點的面稱為π 平面，如圖1 所示。在等傾線上，任意一點對應一個靜水壓力，其應力偏量為零，各個方向受到相同的壓應力或拉應力。在π 平面上只有應力偏量，其靜水壓力為零，主要與物體的塑性變形相關。

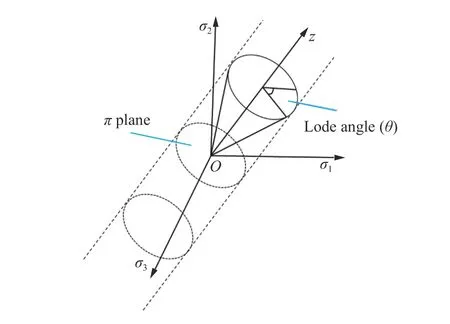
圖1 主應力空間幾何表示Fig. 1 Geometric representation of the principal stress space

應力偏張量與材料的塑性變形相關，表達式為：=σ-σδ， 其中 δ為 Kronecker 符號。應力偏張量的第二不變量和 第三不變量分別定義為：

2 實驗方法及結果

實驗材料為商用Ti-6Al-4V 鈦合金，其原始微觀組織形貌如圖2 所示。分別采用單軸拉伸、單軸壓縮和剪切3 種不同的加載條件進行實驗，獲取材料在廣泛應變率和溫度下的力學特性。單軸拉伸、單軸壓縮和剪切實驗分別采用光滑圓棒試樣、圓柱試樣和新設計的雙剪切試樣，幾何形狀和尺寸如圖3 所示。其中，準靜態實驗采用MTS 萬能試驗機，動態加載采用霍普金森壓桿和拉桿，詳細實驗裝置參見文獻[25]。

圖2 Ti-6Al-4V 材料的原始組織Fig. 2 Microstructure of Ti-6Al-4V material

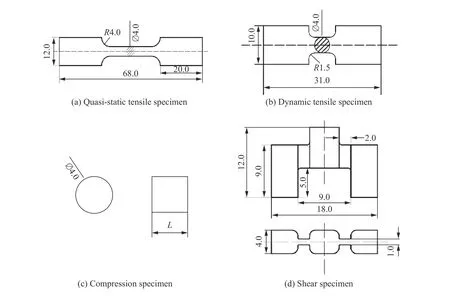
圖3 試樣結構示意圖（單位：mm）Fig. 3 Schematic diagram of the test specimens(unit: mm)

圖4 為準靜態和動態加載時材料在不同應力狀態下的等效應力-等效應變曲線對比圖。在剪切實驗中，假設試樣處于純剪切應力狀態，根據von-Mises 假定，采用下式將剪應力 τ 轉化為等效應力：

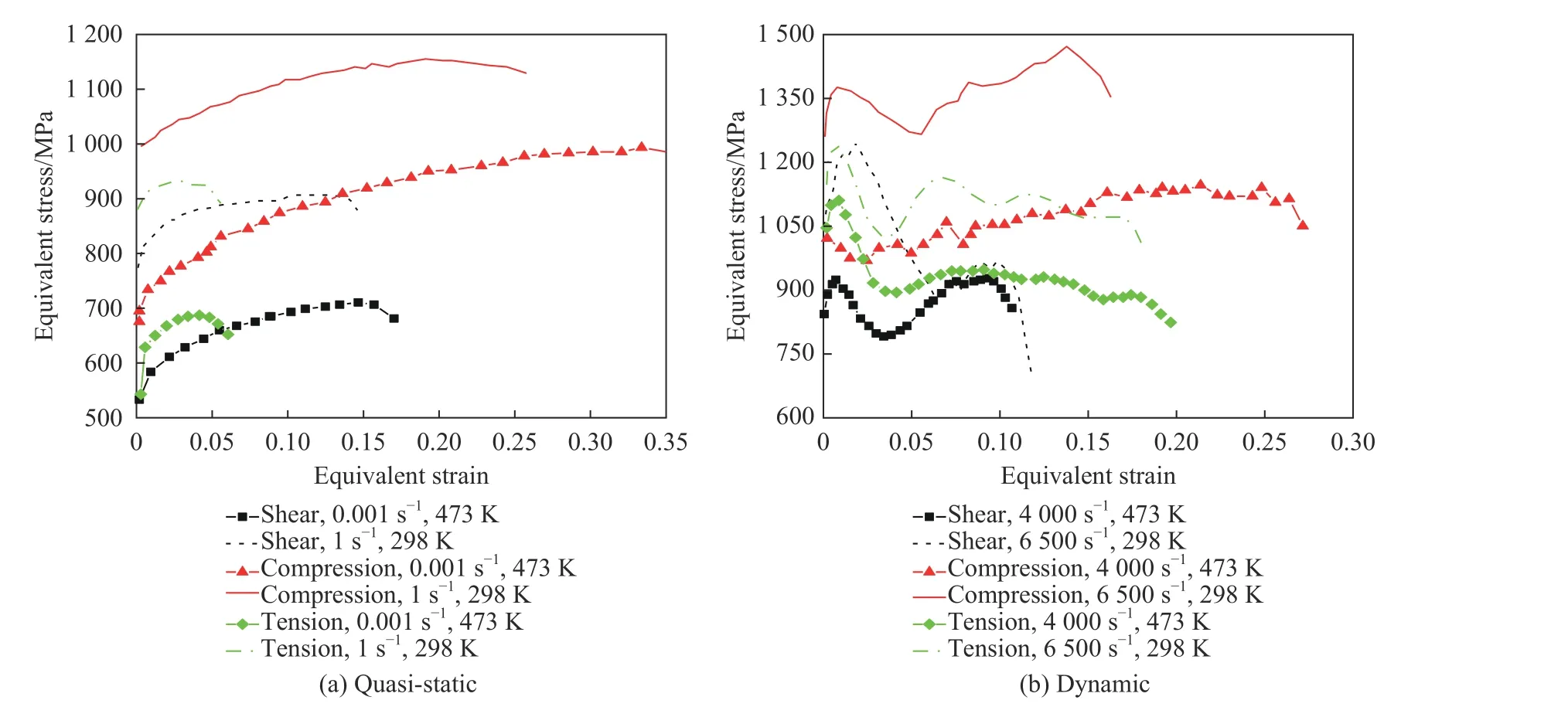
圖4 不同應力狀態下的等效應力-等效應變曲線Fig. 4 The equivalent stress-equivalent strain curves under different stress states

由圖4 可知，在不同的加載條件下，材料的加工硬化效應有所差別。準靜態加載時，Ti-6Al-4V 在拉伸、壓縮和剪切狀態下，隨著塑性應變的增加，材料的流動應力水平明顯增高，其加工硬化效應均較為明顯。然而在動態加載下，只在壓縮狀態下材料表現出明顯的加工硬化效應，可見材料的加工硬化效應與應力狀態相關。此外，無論準靜態還是動態加載等效應力幅值均存在明顯差別，且在純剪切狀態下流動應力水平最低，壓縮狀態下流動應力水平最高。Ti-6Al-4V 材料在拉伸和壓縮情況下的不對稱性與多種因素相關，比如加工方式、晶粒尺寸和材料取向等。在本研究中，所有試樣均沿棒材軸向方向取材，保證材料在拉伸、壓縮和剪切條件下等效應力幅值差別是由應力狀態引起的。因此，為了更好地表征材料的本構行為，應在塑性模型中考慮應力狀態效應的影響。

3 基于應力狀態的塑性本構模型

為了更準確地表征金屬材料的塑性行為，提出一種與材料應力狀態相關的塑性本構模型，即在基本塑性模型的基礎上將應力三軸度和羅德角參數的影響考慮在內。該模型中，材料的流動應力可表示為：式中： σ (ε,ε˙,) 為任意一個包含應變、應變率和溫度效應的塑性本構模型;和分別為應力三軸度和羅德角參數的函數，用于反映應力狀態的影響。根據獲得的實驗數據,和分別采用如下形式：

式中：和 η為與應力三軸度相關的材料參數,和為與羅德角參數相關的材料參數。

由式（11）～（13）可知，可以通過選取適當的模型參數使得 σ 在 η = θˉ=0 時接近于 σ=σ(ε,ε˙,) ，因此可以根據剪切實驗結果確定本構模型 σ=σ(ε,ε˙,) 。工程中常用Johnson-Cook（J-C）模型描述材料的應變率和溫度效應，因此在本工作中選用J-C 模型描述 σ (ε,ε˙,) 。J-C 模型的表達式為：

式中：、、、、為材料常數, ε ˙= ε˙/ε˙為無量綱塑性應變率, ε ˙為參考應變率,為參考溫度,為熔點溫度。在本工作中參考應變率為1 s，熔點溫度為1 941 K，參考溫度為93 K。

采用剪切實驗數據確定J-C 模型的材料參數后，結合拉伸和壓縮加載條件下的實驗結果，可確定模型的應力狀態參數、 η、和。在確定模型參數時，使用回歸分析和約束優化方法使模型的預測結果和實驗數據的誤差最小。在優化過程中，考慮了材料的絕熱溫升。本文中所確定的塑性本構模型參數見表1。

表1 新模型材料常數Table 1 Material constants of the new model

在主應力空間中，該模型的屈服面以及在π 平面上的屈服軌跡如圖5～6 所示，其中圖6 同時給出了Mises 和Tresca 準則的屈服軌跡以方便比較。從屈服軌跡可以看出，在該模型中，當應力狀態發生變化時，屈服面也隨之改變。

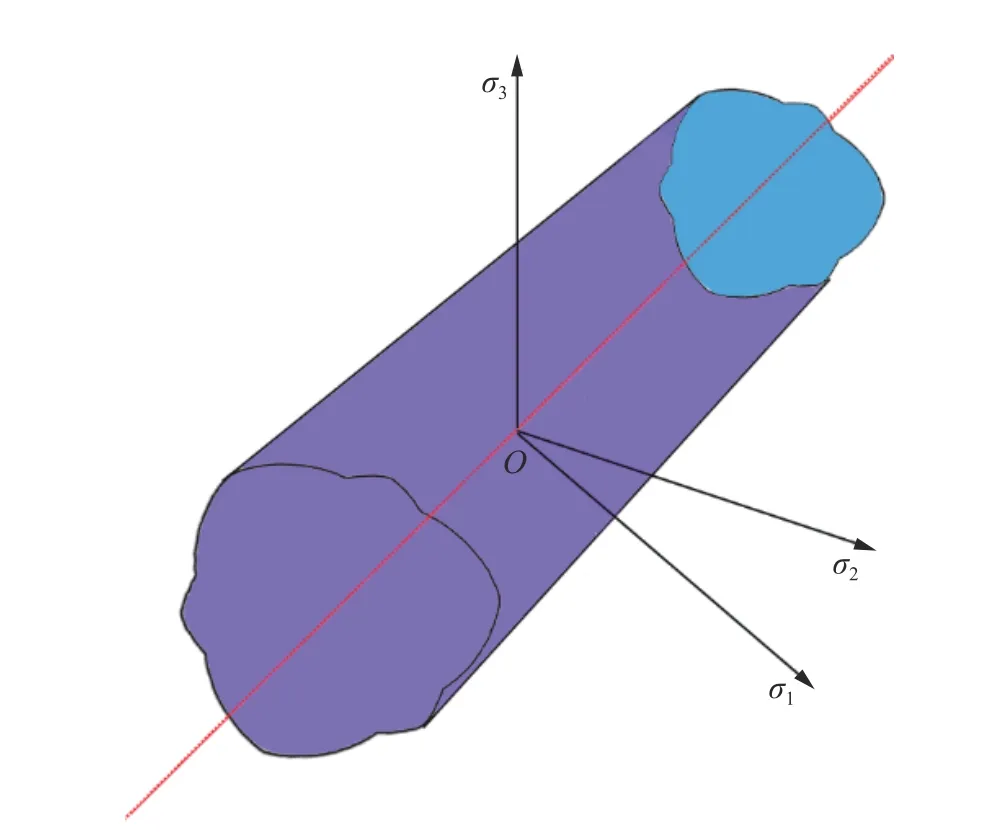
圖5 新模型屈服面Fig. 5 The yield surface of the new model

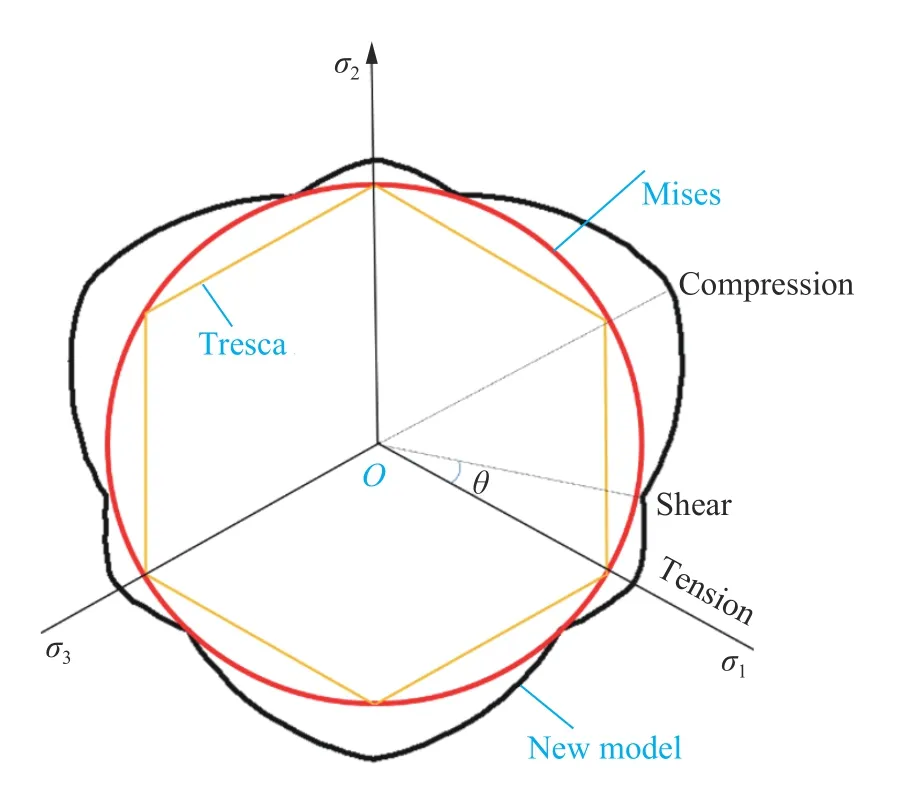
圖6 新模型屈服軌跡圖Fig. 6 The yield locus of the new model

由表1 可知，在簡單剪切狀態下，新提出的塑性本構模型與J-C 模型基本一致。將實驗得到的剪應力和剪應變曲線轉化為等效應力和等效應變曲線，并與模型計算結果進行比較，如圖7 所示。由圖可知，在準靜態加載條件下，該模型與實驗數據吻合較好。在動態加載下，當應變率為1 500 s、溫度為873 K時，模型計算結果稍高于實驗曲線，但誤差仍較小。當應變率進一步提高至6 500 s時，由于應力波的傳播和慣性效應，實驗曲線在初始階段出現較大的震蕩，但其流動應力與計算曲線較為接近。由以上分析可知，該模型可以準確反映剪切條件下材料的塑性流動特性。

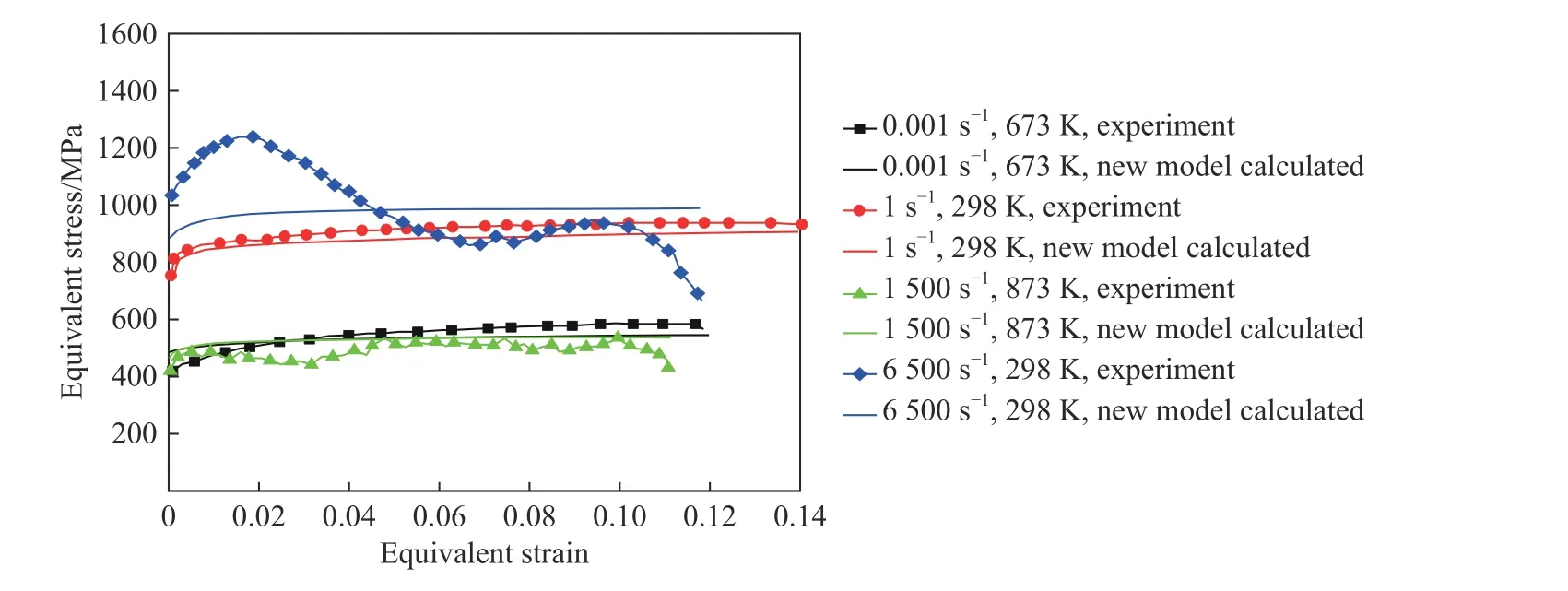
圖7 剪切試驗結果與新模型對比Fig. 7 Comparison of the shear test results with the new model

為了比較J-C 模型和新模型的預測效果，采用下式計算模型與實驗的誤差：

式中： σ為實驗測得的流動應力， σ為本構模型測得的流動應力。

圖8 為不同應變率和溫度下獲得的壓縮實驗曲線，圖中還同時給出了分別由剪切實驗擬合的J-C 本構模型和本文提出的模型所計算得到的應力-應變曲線。由剪切實驗擬合的J-C 模型得到的曲線在準靜態和動態加載情況下均明顯低于實驗曲線，模型與實驗曲線的平均誤差分別為25.2%和21.1%，這是由于J-C 模型未能考慮應力狀態效應對材料造成的影響，因此不能準確反映材料在不同加載條件下的塑性行為；在各應變率下，由新模型得到的應力-應變曲線均接近于實驗結果。在動態加載情況下，實驗曲線存在較大波動，但由新模型給出的兩條曲線均與實驗數據的整體應力水平吻合較好。新模型與實驗結果的平均誤差分別為3.7%、3.9%（見表2）。因此，應力狀態對材料力學性能的影響不容忽視；相比JC 模型而言，新模型可以更準確地預測材料在不同應力狀態下的等效應力-等效應變曲線。

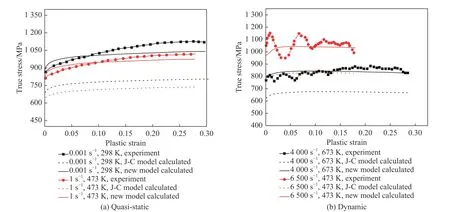
圖8 壓縮試驗結果與兩種模型（J-C 模型和新模型）結果比較Fig. 8 Comparison of the compression test results with the J-C model and the new model

圖9 為在單軸拉伸加載下，實驗結果和兩種模型計算所得應力-應變曲線的對比。在準靜態加載下，由剪切實驗得到的J-C 模型的流動應力水平比實驗值明顯偏低，該現象與單軸壓縮結果類似。在動態載荷下，J-C 模型曲線整體明顯低于實驗曲線；然而，隨著應變量的增加，其流動應力逐漸趨于實驗值。新模型無論在準靜態還是動態加載下，均能較好地反映材料的加工硬化情況和流動應力水平。兩種模型與實驗數據的平均誤差見表2。因此，在拉伸和壓縮載荷作用下，使用新模型能夠更加準確地預測材料的應力-應變曲線，說明該模型可以準確描述材料的應力狀態效應對其塑性流動特性的影響。

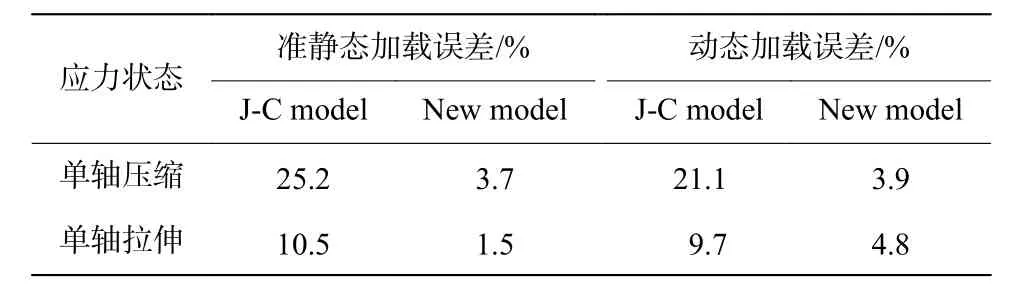
表2 不同應力狀態下新模型和J-C 模型（根據剪切試驗結果建立）與拉壓試驗結果的平均誤差Table 2 Average error of the new and J-C models under different stress states compared with the experimental results

圖9 拉伸試驗結果與兩種模型（J-C 模型和新模型）結果比較Fig. 9 Comparison of the tension test results with the J-C model and new model

4 模型的驗證

為了檢驗所提出的模型對于復雜應力狀態下材料流動特性的預測精度，設計了圖10 所示的壓剪復合試樣并開展動態測試。同時，通過編寫用戶自定義子程序將新模型嵌入ABAQUS 有限元軟件，并對壓剪實驗進行數值模擬。建模時，對入射桿、試樣和透射桿進行三維實體建模，試樣放置在入射桿與透射桿之間，且其端面接觸設置為“硬接觸”，不考慮各接觸面的摩擦效應。入射桿與透射桿均采用C3D8R 六面體縮減積分單元；由于要考慮試樣在加載過程中的絕熱溫升，試樣采用C3D10MT 溫度位移耦合單元。為了更好地模擬剪切區的應力應變場，在試樣剪切區進行局部加密。模型裝配圖如圖10（b）所示，模擬中各部分的材料和物理參數見表3。

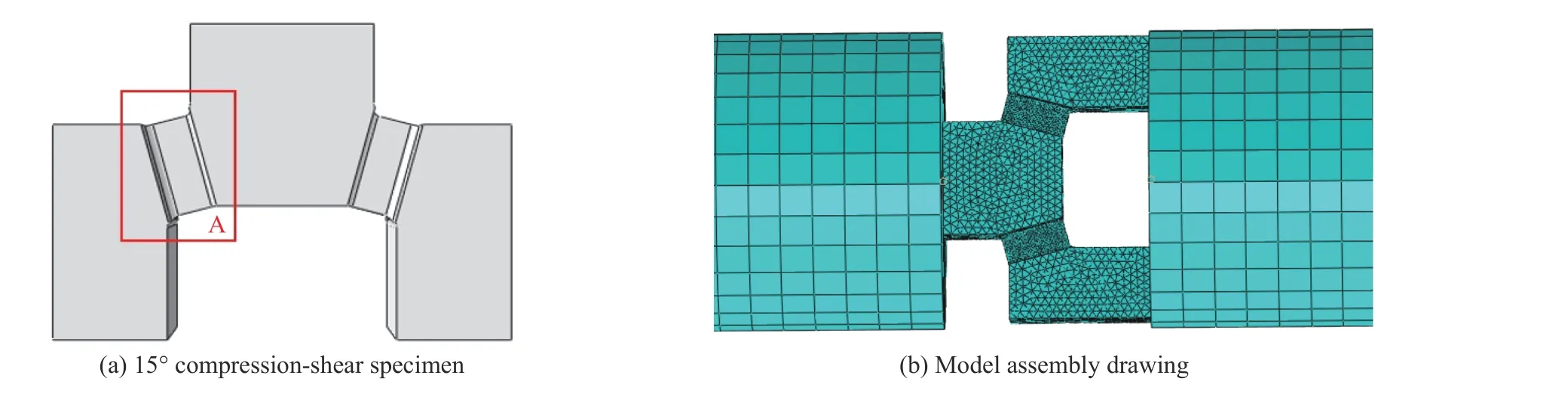
圖10 15°壓剪試樣和有限元模型示意圖Fig. 10 Schematic diagrams of a 15° compression-shear specimen and the finite element model

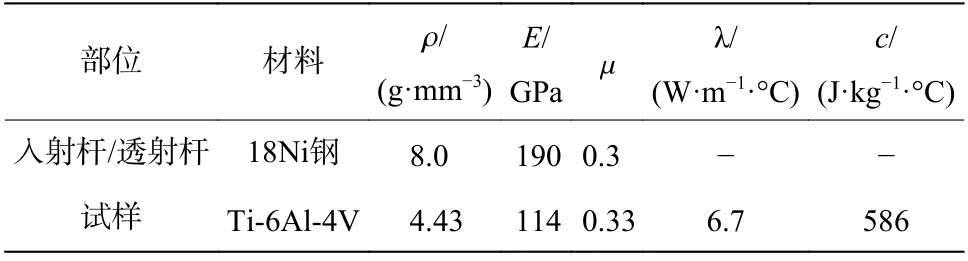
表3 有限元分析中各部件的物理參數Table 3 Physical parameters of each component in the finite element analysis

在數值模擬中分別采用J-C 模型和新模型時，所得到的透射應變脈沖及力-位移曲線與實驗結果的對比如圖11 所示。從壓剪試樣的模擬與實驗對比分析可知，兩種模型均能捕捉到應變波信號的變化趨勢，但J-C 模型明顯低估了實驗數據（見圖11（a））。由圖11（b）可知，J-C 模型和新提出的模型在載荷-位移曲線的上升沿均與實驗數據基本重合。隨著位移的不斷增加，由J-C模型所預測的載荷-位移曲線與實驗曲線出現明顯偏差，而新模型則始終與實驗數據吻合較好。這說明新模型能夠準確預測材料在復雜應力狀態下的塑性變形行為。此外，為了分別研究應力三軸度和羅德角參數對屈服應力的影響程度，圖12 給出了新模型只考慮應力三軸度（=0 ）或羅德角參數（=0 ）時的透射應變曲線和載荷-位移曲線。可以看到，當新模型只考慮羅德角參數的影響時，所得結果與新模型接近，基本可以正確反映材料的流動特性；當只考慮應力三軸度的影響時，其載荷-位移曲線和透射應變信號與實驗結果均相差較大。因此可以看出，對于本文所設計的壓剪試樣，材料的塑性流動特性主要受到羅德角參數的影響，受應力三軸度的影響不明顯。圖13 給出了新模型和J-C 模型在36 、96 、146 μs時所得到的試樣剪切區內部的等效應力分布情況（圖10（a）中紅色框所示的A 區域）。可以看出，在加載過程中，試樣剪切區除邊緣部分外，應力場始終均勻分布，且在相同時刻新模型的等效應力水平均高于J-C 模型，該結果與兩種模型預測的透射應變波信號和力-位移曲線情況相一致。這是由于在壓剪狀態下，材料的流動應力高于純剪切情況下的流動應力，新模型考慮了復雜應力狀態效應對材料塑性特性的影響，而J-C 模型未能考慮該應力狀態效應。因此，新模型可以更加精確地預測材料在高應變率、復雜應力狀態下的力學響應。

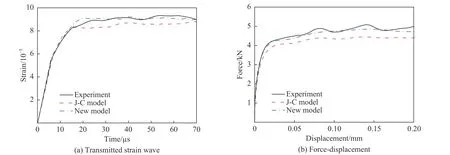
圖11 模擬結果（J-C 模型和新模型）與實驗曲線對比Fig. 11 Comparison of the experimental and simulation results (J-C model and new model)

圖12 模擬結果與實驗曲線對比Fig. 12 Comparison of the experimental and simulation results

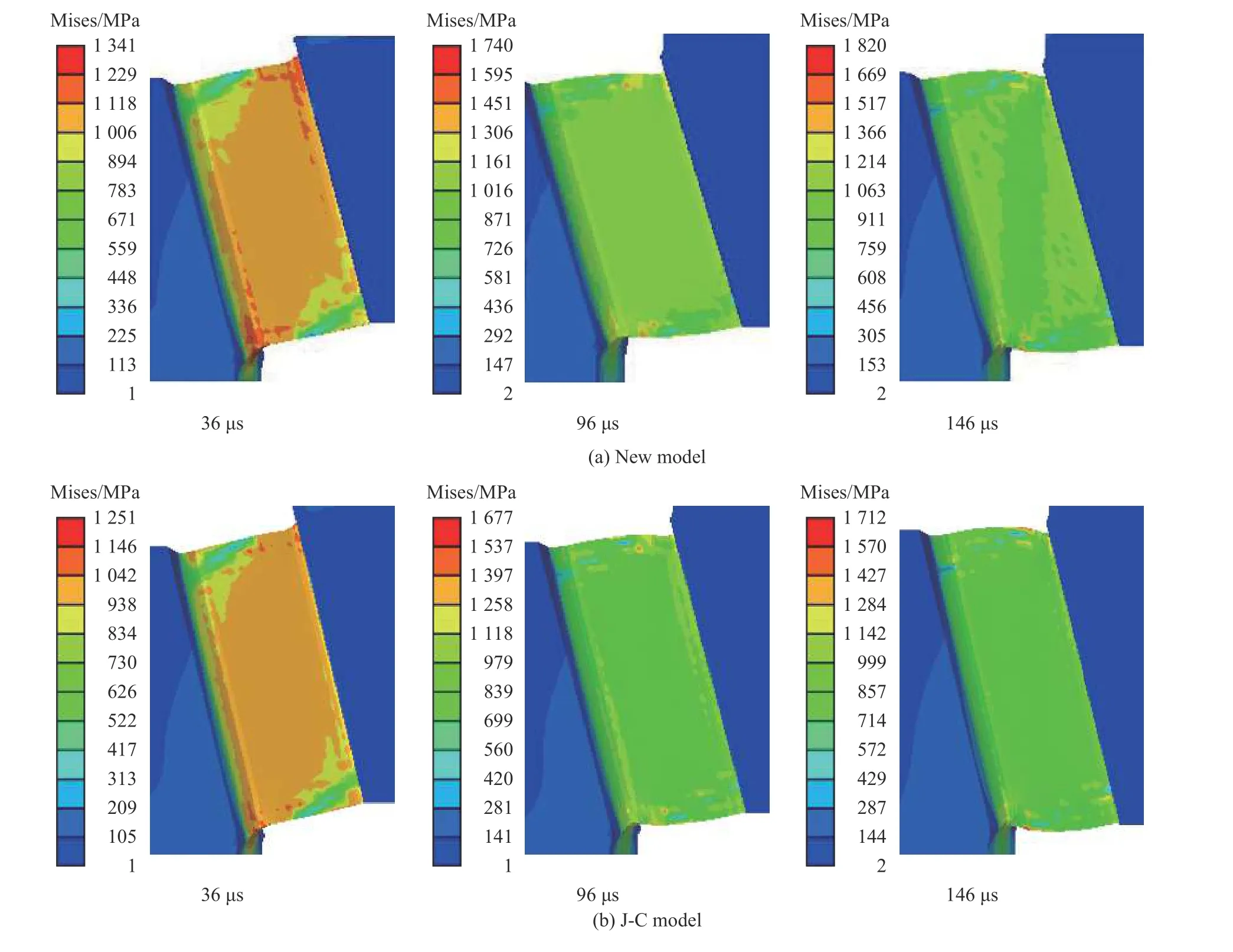
圖13 壓剪試樣在不同加載時刻的等效應力分布Fig. 13 Equivalent stress evolutions of the compression-shear specimen in the simulation

5 結 論

（1）通過對Ti-6Al-4V 鈦合金材料開展單軸拉伸、單軸壓縮和剪切加載下的力學性能測試發現材料的塑性流動應力水平存在明顯差異。壓縮實驗中其流動應力水平最高，剪切流動應力最低，表明應力狀態會影響材料的塑性行為。

（2）提出了一種考慮應力狀態效應的塑性本構模型。該模型考慮了應力三軸度和羅德角參數對流動應力的影響，因此可以對材料在不同溫度、應變率及應力狀態下的力學行為進行描述。

（3）基于Ti-6Al-4V 鈦合金實驗結果確定了新模型的材料參數，該模型對不同應力狀態下的應力-應變曲線的預測結果與實驗結果誤差小于5%。

（4）采用新型壓剪試樣獲得了材料在壓剪復合狀態下的實驗曲線。采用ABAQUS 中VUMAT 用戶子程序對壓剪實驗進行數值模擬，發現新模型的計算結果與實驗數據的吻合程度優于J-C 模型，表明該模型能夠準確描述材料在復雜應力狀態下的塑性行為。