S-LCC型無線電能傳輸系統補償網絡分析

張鵬飛， 龔立嬌,2*， 姚富元， 楊彤， 李紅躍

(1.石河子大學機械電氣工程學院， 石河子 832003； 2.農業農村部西北農業裝備重點實驗室(石河子大學)， 石河子 832003； 3.新疆天富檢測有限公司， 石河子 832000)

針對磁耦合諧振式無線電能傳輸(magnetic coupling resonant radio power transfer, MCR-WPT)系統，配置不同的原副邊側諧振結構，系統的傳輸性能有所不同。并且由于網絡階次的增加，系統的參數優化方法和特性分析也變得復雜[1-2]，因此需對復雜的補償網絡參數進行研究以提高復雜補償網絡的實用性。

文獻[3]詳細分析串聯-串聯(series-series,S-S)、串聯-并聯(series-parallel,S-P)、P-S和P-P 4種基本結構與系統特性，同時以最佳輸出功率為目標給出4種基本結構的原副邊側諧振電容計算公式，但沒有對高階補償網絡參數進行研究。

其次在自然恒流恒壓傳輸特性研究上，文獻[4]提出LCC-S補償拓撲結構下輸出電壓隨著負載電阻的變化而穩定不變。為適應負載在不同情況下的充電特性，文獻[5]在S-P諧振結構基礎上復合CLC型諧振電路，在動態調節中通過交流開關切換諧振結構，實現恒流恒壓傳輸特性；并且文獻[6]在LCL-S諧振結構中改變補償網絡參數，達到恒流恒壓的系統特性。而文獻[7]通過對原邊側諧振電容的改變，達到雙負載自然恒流恒壓的目的。為簡化WPT系統控制的復雜度，文獻[8]采用切換工作頻率的方式，達到切換恒流恒壓的目的，文獻[9-10]在系統電路中增加后級DC/DC單元，從而維持恒定的輸出電壓。

而在補償網絡分析策略上，文獻[11-12]為分析LCL型拓撲結構電路，采用阻抗匹配方法進行補償網絡參數配置，但難以分析副邊側高階補償網絡參數；文獻[13]將系統分成多個子系統，利用A參數描述系統外特性，得出在自然恒壓特性下的不同補償網絡結構，但忽視了系統元件所存在的寄生電阻的問題。而為消除收發線圈寄生電阻的影響，文獻[14-15]構建原邊側分數階電容，使得系統不僅能達到自然恒流特性，同時保證良好的傳輸效率。

在上述文獻研究的基礎上，考慮在實際條件下的電源內阻與元件寄生電阻等情況，現分析S-LCC型拓撲結構系統的傳輸特性，其次探討出在最佳輸出功率情況下原邊側諧振電容計算公式與副邊側諧振電容相互關系。利用原副邊側諧振元件關系簡化輸出功率表達式，確定副邊側諧振電容與諧振電感以及寄生電阻對于最佳負載電阻的影響情況，并分析系統輸出功率隨負載電阻的變化情況，最終通過實物實驗對于理論結果進行驗證。

1 系統數學模型

圖1 S-LCC型MCR-WPT傳輸系統等效電路Fig.1 Equivalent circuit of S-LCC MCR-WPT transmission system

S-LCC型拓撲結構系統的等效電路模型如圖1所示。系統在原邊側通過串聯諧振方式進行連接，其中L1和R1為發射線圈等效參數，C1為原邊側諧振電容，US和RS為高頻電源的等效電壓和內阻。當收發線圈在相同頻率狀態下能量將由發射線圈傳遞給接收線圈，其中L2與R2為接收線圈等效參數，C2、C3、L3和R3分別為副邊側補償網絡的諧振電容、諧振電感以及其寄生電阻。后續子系統采用整流電路和濾波電路對負載RLR進行供電，其中發射線圈阻抗Z1=R1+jωL1，接收線圈阻抗Z2=R2+jωL2，Z3=R3+jωL3為諧振電感的實際阻抗且收發線圈互感為M12;ω為電流頻率；j為虛數。

根據文獻[10]所知，系統的整流濾波電路與負載電阻RLR可以等效為電阻RL，即

(1)

(2)

式(2)為整個系統的回路電路方程，其中當電流頻率ω達到收發線圈諧振頻率點時，可得到輸入電流I1與輸出電流I3的有效值表達式，即

(3)

式(3)中:M12為兩側線圈互感值；Z1、Z2和Z3為兩側線圈阻抗和副邊側補償網絡阻抗；Δ為整體電路阻抗矩陣的行列式，其具體表達式為

(4)

搭配合適的整流濾波電路[7]根據輸出電流表達式，得到輸出功率表達式為

(5)

由式(5)可知S-LCC型拓撲結構下輸出功率P與電源等效電壓US、等效電阻RS、線圈互感M12、負載電阻RL和補償網絡參數有關。而本文在研究補償網絡對系統傳輸特性的基礎上，對補償網絡元件和最佳負載電阻的相互關系進行詳細討論。

2 恒流恒壓下補償網絡分析

由上述的分析結果可得系統的輸出電壓表達式為

(6)

式(3)和式(6)表明在互感M12與電源電壓US不變的條件下，要使系統的輸出電流I3與輸出電壓Uo保持恒定，就需要改變補償網絡參數。

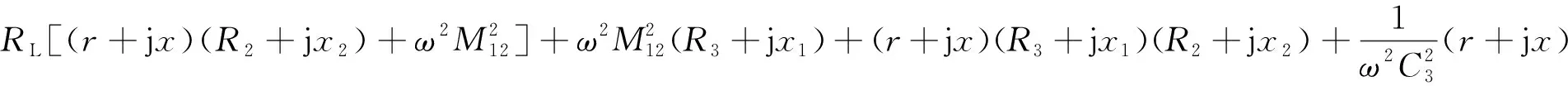
(7)

為分析系統外特性，將式(4)轉換為式(7)，式(7)中原邊側等效電阻r和等效電抗x與副邊側等效電抗為x1和x2表達式，如式(8)所示：

(8)

當阻抗矩陣行列式Δ的第一部分為零時系統可達到恒流狀態；當Δ的后續部分為零時系統可達到恒壓狀態。

2.1 恒流諧振參數

研究以恒流傳輸特性為目的的補償網絡時，相關文獻基本會忽略系統元件寄生電阻與電源電阻的影響，因此系統達到恒流特性的參數關系為

(9)

而在不可忽視系統電阻的條件下，由式(7)可知，當阻抗矩陣行列式Δ不含RL參數時，即滿足式(10)關系時，輸出電流I3才有達到恒定的可能。在參數表達式(11)中，由于原邊側等效電阻r、接收線圈等效電阻R2與收發線圈互感M12皆為正數，式中的第一組關系式要求電抗xx2>0；而第二組關系式要求xx2≤0。兩者相互矛盾，顯然S-LCC型拓撲結構不存在恒流特性。

(10)

2.2 恒壓諧振參數

同理在理想條件下，即不考慮收發線圈等效電阻與電源電阻，確定具有恒壓特性的補償網絡參數表達式為

(11)

而在實際條件下，若將式(8)中的后兩部分清零,輸出電壓Uo可不受負載電阻RL的影響。最終得出具備恒壓特性的參數表達式，即

(12)

式(12)中:R3為副邊側補償網絡中諧振電感的寄生電阻，而不論收發線圈處于諧振狀態還是接近諧振狀態下，R3值較小基本可以忽略。

需要注意是S-LCC型拓撲結構系統配置的原副邊側諧振電容參數含有三組，但式(12)僅含有兩組關系式，因此需要分情況進行說明。

(13)

(14)

其次考慮當原邊側等效電抗x不為零狀態下，系統具備恒壓特性的可能。當系統處于理想諧振狀態下，即收發線圈等效電阻R1=R2≈0時，利用假設條件得出式(14)。根據式(14)可得出副邊側等效電抗x1和x2相互矛盾，系統無法達到恒壓特性。

(15)

尤其處于高頻非諧振狀態下，線圈等效電阻遠大于補償電感的寄生電阻R3時，即線圈內阻R1=R2≠0，最終可得出具有恒壓特性的參數表達式:

(16)

化簡式(15)可得到式(16)，確定副邊側回路電抗x1=0，但與式(15)關系式組相矛盾。

最終確定在實際條件下，不論是原邊側等效電抗x是否為零，還是整個系統是否處于諧振狀態，整個S-LCC型無線電能傳輸系統都不具備自然恒壓特性。

一種意識的變革隱藏在這些藝術家一系列循序漸進的實踐中，在這一時期、這一領域的雕塑中，體積和容積不再是雕塑的唯一表現手段，從對動感的追求到真正使雕塑運動起來，成為當時藝術創作的重要元素。 拉茲洛·莫霍利·納吉(LaszloMoholyNagy)還在一則宣言中為活動的藝術提供了一套理論，他主張以能量間的關系取代傳統藝術觀念中形體間的關系，以“動態——解構”系統為手段使空間活動起來。至此，動態雕塑獲得了實踐與理論的支持，成為了一種新興的藝術形式。

3 最佳輸出功率下補償網絡分析

3.1 補償網絡參數分析

為確定最佳輸出功率下的原副邊側補償網絡參數，一般采用阻抗匹配方法將副邊側等效阻抗“反映”到原邊側回路中，進行原副邊側補償網絡參數的配置，但阻抗匹配策略適用于忽略電源電阻與元件電阻的情況。而在不可忽略線圈等效電阻與電源電阻的情況下，本節利用推導出的輸出功率表達式，確定最佳輸出功率下原邊側諧振電容計算公式與副邊側諧振電容之間相互關系。

首先求出原邊側諧振電容C1計算公式，由式(5)可得到輸出功率P與輸出電流I3的平方成正比關系,因此在固定負載情況下追求最大輸出電流，也是間接得到最佳輸出功率。由式(1)～式(5)可知在復雜拓撲結構下補償網絡參數確定比較困難。本文將阻抗矩陣行列式Δ轉化為式(17)，由式(3)可知Δ最小時，輸出電流達到峰值。

(17)

觀察式(17)可發現C1和發射線圈等效阻抗Z1具有“獨立性”，與副邊側補償網絡參數無關。由此可假設副邊側諧振電容參數C2與C3為“常量”，與原邊側諧振電容C1無關。因此要使Δ最小，則需要滿足：

(18)

最終可得：當處于最佳輸出功率下S-LCC型拓撲結構無線電能傳輸系統中原邊側諧振電容關系與S-S型拓撲結構系統關系[3]相同。

其次討論S-LCC型拓撲結構系統中副邊側諧振電容C2與C3關系。在固定諧振電感L3的情況下，諧振電容C2僅含于阻抗矩陣行列式Δ中，因此對于諧振電容C2的研究應轉化為對Δ的討論。

將原Δ表達式化簡為式(19)，其中部分參數意義與上節參數相同，新增參數意義為r1=RL+R3。將式(5)中阻抗矩陣行列式Δ2化簡為式(20)。

(19)

(20)

由于諧振電容C2僅存在阻抗矩陣行列式Δ的x2中，因此將對C2微分改為對x2的微分，即

(21)

化簡式(21)，得出副邊側諧振電容C2與C3的關系，如式(22)所示。由式(23)和式(24)得出在最佳輸出功率下系統輸出功率P與輸出電流I3的表達式。

根據下文所采用的系統參數，得出在固定負載電阻RL=200 Ω情況下，輸出功率P與輸出電流I3隨著諧振電容C3的變化情況如圖2所示。

圖2 輸出功率、輸出電流與諧振電容的關系Fig.2 Relationship between output power, output current and resonant capacitance

由圖2可知，隨著諧振電容C3的增加，輸出功率P會表現出先增加后減少再增加的趨勢，其中當諧振電容C3=7.6 pF時輸出功率達到最大值為3.51 W；輸出電流I3值|I3|隨著諧振電容C3的增加而表現出與輸出功率相同的趨勢，在同一諧振電容處輸出電流達到最大值為0.15 A，這可驗證3.1節所提出的間接追求最佳輸出功率的策略。

由此可知在固定負載電阻情況下配置合適的原副邊側諧振電路可使系統輸出最佳功率。而當補償網絡參數發生變化時就需要改變負載電阻，使得系統輸出最佳輸出功率。因此分析驗證最佳負載電阻隨補償網絡參數變化情況是十分有意義的。

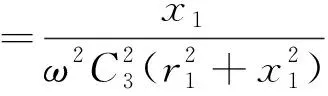
(22)

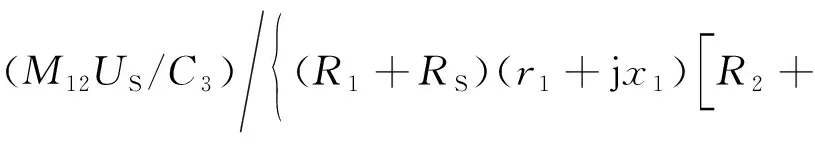
(23)

(24)

3.2 遠距離傳輸分析

3.1節中在固定負載電阻的情況下研究補償網絡中諧振電容的關系，而本節考慮在遠距離傳輸條件下，研究諧振電感的寄生電阻R3與諧振電容C3對最佳負載電阻RLo的影響情況。

系統在長距離傳輸能量過程中，根據上文補償網絡參數分析結果，可忽略輸出功率分母部分中線圈互感M12的影響，簡化輸出功率表達式，最終轉化為含有諧振電容C3、諧振電感L3與負載參數RL的公式為

(25)

參數λ表達式為

(26)

如圖3所示，采用系統仿真參數，可看出當整個S-LCC型拓撲結構系統配置不同的補償網絡時，需要“加載”的最佳負載電阻RLo會呈現出隨著諧振電阻R3的增加而增加，隨著補償網絡等效電抗值|x1|的增加而增加的趨勢。

根據這種現象，本節探討副邊側諧振電路中補償電感寄生電阻R3與諧振電容C3對整體系統的影響。首先假定收發線圈為理想線圈時，利用式(25)對負載電阻RL進行求導,得出最佳負載電阻所需參數表達式：

(27)

根據微分方程[式(27)]，令函數F為

(28)

其中函數F初值為

(29)

由式(30)可知，在固定負載電阻RL情況下，最優副邊側諧振電抗值|x1|會隨著補償網絡的寄生電阻R3增加而增加。

而研究諧振電感的寄生電阻R3對最優負載電阻RLo的影響時，利用式(28)對函數F進行微分操作，結果為

(30)

(31)

當負載電阻RL無窮大時，函數F必然大于零。根據式(29)與式(31)可知函數F存在兩個過零點，由求導公式(27)可知輸出功率會隨著負載電阻的增加而表現出先增加后減少再增加的趨勢。

由此在遠距離傳輸情況下，系統輸出功率會隨著負載電阻RL的增加而呈現出先增加后減少再增加或者一直增加的趨勢，如圖3中①和②所示(以右坐標數值為輸出功率)。

其次諧振電感的寄生電阻R3增加時，函數F初值變大，而從式(30)得出函數F減小趨勢變緩，因此最佳負載電阻RLo不斷增加。

(32)

圖3 不同參數條件下輸出功率變化情況Fig.3 Variation of output power under different parameter conditions

但隨著負載電阻的不斷增加，輸出功率分母中有關互感和負載電阻部分起著越來越重要的作用。因此為更全面分析系統的輸出功率變化趨勢與最佳負載電阻情況，就必須考慮系統中原副邊側互感M12，忽略諧振電感寄生電阻R3。

3.3 近距離傳輸分析

當系統處于強耦合狀態時，忽略諧振電感的寄生電阻R3，本節分析系統的輸出功率變化趨勢與諧振電容C3和諧振電感L3對最佳負載電阻RLo的影響。

可將輸出功率表達式轉化為

(33)

式(33)中：參數λ1表示為

(34)

與3.2節分析方法相同，利用式(33)建立微分方程，可得出最佳負載電阻RLo所需參數條件。建立函數F1，如式(35)所示。

(35)

函數F1的初值與終值為

(36)

利用式(38)建立微分方程為

(37)

當RL=|x1|時微分方程的最大值為

(38)

縮短傳輸距離使得互感M12為20 μH，如圖4所示。若原副邊側補償網絡參數滿足使式(38)小于零時，則表明函數F1會隨著負載電阻RL的增加而不斷減少，且當RL=|x1|時函數F1=0，說明整個系統存在最佳負載電阻且輸出功率P會隨著負載電阻的增加而呈現出先增加后減少的趨勢，如圖4中③和④所示(以右坐標數值為輸出功率)。

其次若補償網絡參數使式(38)大于零時，由上文可知F1(∞)<0，函數F1初值大于零且當RL=|x1|時函數F1等于零，說明整個系統存在負載電阻RL1小于|x1|和負載電阻RL2大于|x1|使得系統達到最佳輸出功率。

由此可看出系統輸出功率會隨著負載電阻的增加而表現出先增加后減少或者先增加后減少再增加又減少的趨勢。

分析諧振電容C3和諧振電感L3對于最佳負載電阻的影響情況，當式(38)小于零時最佳負載電阻RLo=|x1|，此時當副邊側等效回路電抗x1<0時最佳負載電阻呈現隨著諧振電感的減少而不斷增加，隨著諧振電容的減少而增加的趨勢。而當x1>0時最佳負載電阻隨諧振電感的減少而減少，隨著諧振電容的減少而減少。

圖4 不同參數條件下輸出功率變化情況Fig.4 Variation of output power under different parameter conditions

而當式(38)大于零時，最佳負載電阻需滿足式(35)等于零，因此設計函數與目標函數為

(39)

(40)

由式(38)可得出最佳負載電阻RL1與RL2應滿足：

(41)

在固定諧振電容的情況下函數M目標值Mg為穩定值。其中函數M最小值為2|x1|，而當諧振電感L3減少時，若x1>0時函數M最小值減少且函數前半段減少趨勢變緩，同時由式(41)可知較小的最佳負載電阻RL1隨著諧振電感的減少而不斷減少，最佳負載電阻RL2隨著諧振電感的減少而增加。

當x1<0時同理可知最佳負載電阻RL1隨著諧振電感L3的減少而增加，RL2隨著諧振電感L3的減少而增加。

而研究諧振電容C3對最佳負載電阻的影響時，設計和化簡函數T并在RL<|x1|對諧振電容C3進行求導，如式(42)所示:

(42)

在x1>0時可知隨著諧振電容C3的減少，在相同負載電阻情況下函數T相對變小，且|x1|值減少時函數T初值變小，由式(41)可得出最佳負載電阻RL1隨著諧振電容的減少而減少，RL2隨著諧振電容的減少而增加。同理在x1<0時最佳負載電阻RL1隨諧振電容的減少而增加。

4 仿真與實物實驗驗證

為驗證本文所提出的副邊側補償網絡諧振電容關系與不同補償網絡參數對輸出功率影響結果的正確性，利用阻抗分析儀對實物線圈進行測量，且在諧振頻率點處測出線圈參數，最終得出相關參數進行仿真實驗分析，具體仿真實驗參數如表1所示。

搭建實物實驗系統如圖5所示，采用信號發生器與功率放大器設計目標頻率的輸入電源與輸入電阻，利用電容C1、C2、C3與諧振電感組成原副邊側補償網絡元件，搭建合適的整流與濾波電路對負載電阻進行供電，圖5中示波器對輸出電壓進行檢測。

表1 S-LCC型拓撲結構系統參數Table 1 System parameters of S-LCC topology

圖5 S-LCC型拓撲結構系統實物實驗圖Fig.5 Physical experiment diagram of S-LCC topology system

4.1 副邊側諧振電容關系驗證

如圖6所示，在固定負載電阻RL=201.2 Ω情況下，當選擇不同組的諧振電容C2、C3時,輸出功率P都會隨著諧振電容C2的增加而表現出先增加后減少的趨勢。圖6中參考線①、②、③依次為公式得出在諧振電容C3依次減少時的最佳諧振電容C2值。其中可發現在不同諧振電容C3條件下通過實驗測出最佳諧振電容C2值與式(22)得出最佳諧振電容C2基本相同，從而驗證本文得出的副邊側諧振電容關系。

圖6 接收線圈諧振電容關系驗證Fig.6 Verification of the relationship between secondary side resonant capacitance

4.2 遠距離傳輸分析驗證

設定諧振電容C3=8 pF時，通過改變寄生電阻R3，如圖7(a)所示，隨著寄生電阻R3的增加，最佳負載電阻由142 Ω增加到155 Ω。同樣在C3=25 pF的情況下，如圖7c所示，最佳負載電阻會隨著寄生電阻的增加而由132 Ω增加到150 Ω，都呈現出緩慢上升的趨勢。

在寄生電阻R3=3.5 Ω時，設定諧振電容C3=10 pF基礎上不斷減少，如圖7(b)所示，最佳負載電阻從142 Ω增加到192 Ω。同理設定諧振電容C3而在25 pF基礎上不斷增加，如圖7(d)所示，最佳負載電阻也由132 Ω增加到190 Ω。這符合3.2節諧振電容與寄生電阻對最佳負載電阻影響結果的相關結論。

圖7 寄生電阻與諧振電容分析驗證Fig.7 Analysis and verification of parasitic resistance and resonant capacitance

4.3 近距離傳輸分析驗證

減少線圈間傳輸距離使得互感M12=6.38 μH，確定諧振電感L3=50 μH，如圖8(a)所示，依次減小諧振電容C3，輸出功率P都會隨著負載電阻RL的增加而出現先增加后減少的趨勢，清晰看出隨著諧振電容C3不斷減少，最佳負載電阻也從164 Ω增加到214 Ω。同理設置諧振電容C3在23.5 pF的基礎上不斷增加，如圖8(c)可看出最佳負載電阻由152 Ω增加至214 Ω。

如圖8(b)所示，設定諧振電容C3=10 pF時，通過減少諧振電感L3，最佳負載電阻也從164 Ω增加到210 Ω；當諧振電容為24 pF時，改變諧振電感由48 μH增加到51 μH，如圖8(d)所示，可發現最佳負載電阻從125 Ω增加到210 Ω。由實驗結論可驗證出3.3節諧振電容與諧振電感對最佳負載電阻影響結果的相關結論。

圖8 諧振電感與諧振電容分析驗證Fig.8 Analysis and verification of resonant inductance and resonant capacitance

5 結論

本文的研究目標是在S-LCC型拓撲結構無線電能傳輸系統的基礎上,以研究諧振參數關系來達到系統最佳特性為目的。最終得出以下結論。

(1)分析補償網絡中諧振電容的相互關系。最終確定在最佳輸出功率的情況下原邊側諧振電容的計算公式與副邊側諧振電容之間的相互關系。

(2)討論系統的恒壓恒流特性。在不同參數情況下確認S-LCC型結構電路不存在自然恒壓恒流的可能性。

(3)在研究諧振電容對系統最佳負載電阻影響的基礎上，依次考慮諧振電感以及其寄生電阻參數，最終得出：系統的輸出功率會隨著負載電阻的增加而先增加后減少再增加又減少或者先增加后減少；系統的最佳負載電阻隨著諧振電容C3的減少而先減少后增加，隨著諧振電感的減少而先減少后增加，隨著諧振電感寄生電阻R3的增加而增加。