改進非線性外源自回歸網絡的潮位實時預測

李連博， 武文昊， 章文俊， 尹建川， 朱振宇

(1.大連海事大學航海學院， 大連 116026； 2.廣東海洋大學海運學院， 湛江 524088)

潮汐是在月球和太陽引力作用下形成的海水周期性漲落現象，是重要的海洋物理要素之一，潮汐預報是港口與航道管理、水運資源開發、海洋資源利用、救生打撈和海上軍事活動等涉海人類活動的基礎數據支撐技術手段。隨著科學技術的發展，潮汐預報在航海中的影響逐漸增大。尤其是大型船舶，在進出港口、通過淺灘及架空障礙物等情況中，如果能及時準確地得到潮汐數據，船舶的運營效率和航行安全就能得到保障，從而避免船舶擱淺、刮碰橋梁或船體傾覆等危害海上安全的事故[1]。

關于潮汐的預測最常用的是數學統計方法，從最初的潮波微分方程到潮汐調和分析以及潮汐響應分析，不斷衍生出更精確的數學模型，近年來依然有新方法被提出。Tawil等[2]就潮汐預報提出了兩種方法，即基于全三維數值方法和基于潮流的線性逼近方法，其中前者對數據的需求量大，耗時長，但是結果精確，后者可以在很長一段時間內對潮流數據進行非常快速的評估，但準確性有所下降； Okwuashi等[3]根據偏最小二乘擬合回歸法 (partial least squares regression, PLSR) 建立模型來預測潮位，在傳統最小二乘模型 (LS) 基礎上進行了優化提升，通過減少回歸方程的數量并丟棄冗余系數，最終確定最有效系數，預測精度也較傳統LS模型得到了提升。王森等[4]提出了一種基于全球衛星定位系統的多路徑反射測量技術用于潮位預測，結果顯示所提出的方法與實測數據相關性為0.97，預測精度可達分米級，但是由于調和分析方法的局限性，無法克服非線性氣象因素的影響。可見數學方法計算步驟復雜，數據需求量大以及易受各種隨機干擾影響的缺陷。

近年來，人工智能技術迅猛發展，由于其較強的搜索，推理，規劃和自學習能力，在工程計算領域得到了廣泛的應用，如人工神經網絡(artificial neural network, ANN)、長短期記憶網絡(long short-term memory, LSTM)[5]、模糊神經網絡(fuzzy neural networks)[6]、小波神經網絡(wave neural networks, WNN)[7]、徑向基函數神經網絡(radial basis function, RBF)[8]等，同時在潮位預測方面出現了眾多成果，Raj等[9]利用ANN對澳大利亞北部海岸線周圍平均海平面進行了預測，在選取的4個站點均取得了良好效果，預測值的均方根誤差最低達0.04 m，但是不能證明該研究的普適性和泛用性；Tu等[10]提出了一種新的實時潮位預測方法，首先利用調和分析來預測天文潮汐，再通過LSTM網絡和逆距離加權及其插值算法對整體預測結果進行校正。實驗結果顯示預測相關系數為0.98，均方根誤差最低達0.05 m，由于模型僅考慮了風對結果的影響，可見預測精度可進一步優化；Granata等[11]提出了一種M5P回歸樹模型用于預測威尼斯城的潮位，結果表明預測相關系數可達0.99，相對絕對誤差 (RAE) 最低為5.98%，但是沒有考慮氣象因素；總的來看，目前針對潮汐預報的研究成果已相對完善，預測精度也相對較高，但仍存在一些不足，如預測結果不穩定、需求數據量過大、非線性因素干擾等問題。

在預報潮位時，潮位數據可以看作時間序列。NARX 神經網絡的結構特點使得它針對時間序列有更好的學習效率，并且有更高的預測精度。此前已有多個成功應用NARX神經網絡預測數據的實例[12-16]，其應用從工程計算領域到金融領域均有涉及，且針對動態時間序列預測效果尤為出色，但目前暫時沒有應用于潮汐預測領域。鑒于NARX神經網絡在預測方面的優勢，同時為了克服目前潮汐預測模型存在的缺陷，提出一種基于改進的NARX神經網絡的實時潮汐預報模型(MS-NARX)，其結構簡單，預測結果精確穩定，能充分結合非線性氣象因素進行預測，將該模型帶入實測潮位數據進行仿真預測，同時選取傳統NARX以及SAPSO-BP神經網絡的預測結果作為對照來驗證MS-NARX神經網絡預測的可行性。

1 潮位預測方法

1.1 傳統NARX神經網絡

NARX神經網絡是一種用于描述非線性離散系統的模型，全稱為非線性自回歸模型[17-19]，是非線性動態系統中，應用最廣泛的一種神經網絡,且適用于時間序列預測，并已被應用于解決多個領域的非線性序列預測問題，其對歷史數據的記憶作用增強了其對動態數據的處理能力，提高了對復雜序列的預測性能[20-23]。基本結構如圖1所示。

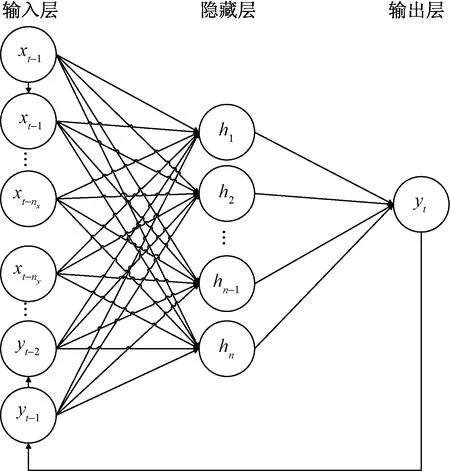
xt為神經網絡的外部輸入；h1, h2, …,hn為神經網絡內部隱藏層的各神經元；yt為神經網絡在t時刻輸出；xt-1和yt-1分別為t-1時刻的神經網絡的輸入和輸出圖 1 NARX神經網絡結構示意圖Fig.1 NARX neural network structure diagram

NARX神經網絡的模型為

yt=f(yt-1,yt-2,…,yt-ny,xt-1,xt-2,…,xt-nx)

(1)

式(1)中:nx和ny為輸入和輸出的最大時延階數；f為網絡擬合得到的非線性函數。由式(1)可知，NARX神經網絡的輸出受前一時刻輸入及輸出數據的影響，標準的NARX神經網絡結構中采用閉環模式，神經網絡的輸出反饋給輸入，如圖2所示，圖2中TDL(tapped delay line)表示時延階數。然而，由于NARX神經網絡訓練的預期輸出是已知的，因此建立了圖3所示的串并聯神經網絡的開環模型。在這種模式下，所需的輸出被反饋到輸入端。這種方法有兩個優點：一是NARX神經網絡的預測效果更準確；二是將NARX神經網絡轉化為一個簡單的前向神經網絡，可以利用靜態神經網絡的建模功能。由于NARX神經網絡的期望輸出是已知的，是實測潮位數據，因此采用串并聯模型進行訓練和預報[24]。

圖2 NARX神經網絡的兩種結構圖Fig.2 Two structural diagrams of NARX neural network

為了使預測結果更加穩定，在NARX模型的基礎上加入了模塊化潮汐預報方法，天文潮部分主要由天體引潮力引起，具有明顯的變化規律; 非天文潮部分受到環境因素影響，其變化沒有明顯規律，展現出很強的隨機性。該模型首先利用調和分析法的天文潮部分，獲得潮汐的整體變化規律，再利用NARX神經網絡結合滑動時間窗對非天文潮部分進行預測，修正預測結果，達到精確預報潮汐的目的。具體步驟框圖如圖3所示。

圖3 MS-NARX神經網絡的潮汐預報模型框圖Fig.3 Tidal prediction model block diagram of MS-NARX neural network

1.2 調和分析法

根據對于潮汐的長期觀測得知，潮汐是由一系列諧波振動，即分潮組成的。分潮的周期同引潮力各分力場的周期相互對應。潮位Yt計算公式[25]為

(2)

式(2)中：A0為平均潮位高度；N為分潮的總數；hi為各分潮的振幅；ωi為各分潮頻率；εi為各分潮相位。

為了簡化，相位通常近似為0，式(2)也可轉化為

(3)

Ai和Bi為分潮的兩個系數且與hi及εi有如下關系，可以從一個月以上的潮汐預報數據中求出。

(4)

(5)

調和分析法是潮汐預報方面最傳統的技術[26]，簡單實用，但也存在缺點。首先，調和分析通常使用18 a以上的歷史記錄來提取所有分潮數據，通常情況下，可用的歷史記錄數量很少，從而導致誤差增大；另外，分潮的選取與觀測時段的長度以及觀測記錄之間的時間間隔都有關系，如果與這兩者搭配不好的話，就可能得到不準確的結果，甚至可能計算不出結果[27-28]。本文選用了T-tide工具包來計算潮汐調和分析的數據，輸入參數包括要分析的潮位數據，數據的間隔設置為1 h，驗潮站的經緯度25° 43.9′N、80° 9.7′W，數據的起始時間是2020年6月1日GMT0000。輸出參數包括調和分析得到的分潮的名字，根據數據的長度確定，越長的數據得到的分潮越多。由于數據有限，本文在基礎的四大分潮 (M2，S2，K1，O1)之外僅額外取得了4個分潮 (M4, Q1, P1, K2)。另外輸出參數還包括分潮的角速率，分潮振幅以及振幅的誤差，分潮遲角以及遲角的誤差。通過信噪比(SNR)來衡量分潮是否顯著，計算公式為

(6)

式(6)中：hi為分潮振幅；Δhi為振幅誤差；一般情況下SNR>2的分潮是顯著分潮。綜合以上輸入和輸出參數，通過MATLAB軟件運行T-tide工具包最終可得到調和分析回報的天文潮位。

1.3 SAPSO-BP神經網絡

基本反向傳播BP(back propagation)神經網絡是一種按照誤差逆向傳播算法訓練的多層前饋神經網絡，是目前應用最廣泛的神經網絡。該網絡主要包括信號前向傳遞和誤差反向傳播兩個方面，即計算實際輸出時按從輸入到輸出的方向進行，而權值和閾值的修正從輸出到輸入的方向反向進行。如果輸出層得不到實際輸出，則轉入反向傳播，根據預測誤差調整整個網絡的權值和閾值，從而使BP神經網絡預測輸出逐漸向實際輸出靠攏[29]。

BP神經網絡在應用中由于采用了非線性規劃中的最速下降法，通常存在容易陷入局部極小狀態以及收斂速度慢，學習效率低等缺點，其預報結果還有很大提升空間，所以本文引入了自適應粒子群(SAPSO)算法對BP神經網絡進行優化。粒子群算法源于模擬鳥群捕食的行為，鳥群中的每只鳥代表每個粒子，食物代表優化解，算法的運算原理如下：首先隨機生成一組作為隨機解的粒子，以及各自在搜尋空間中的位置和速度，每個粒子都有對應的由所優化的問題決定的適應度函數值。每一次迭代循環過程中，每個粒子以一定的速度通過跟蹤個體極值和群體極值來更新自身的位置，個體極值是粒子在尋優過程中自身所尋找到的最優值，而群體極值則是整個種群在尋優過程中獲得的全局最優值。為了加強優化性能，借鑒了遺傳優化算法中的變異方法(simple mutation)，在基礎粒子群優化的基礎上引入了自適應變異算法SA(self-adaptive)，即在每次粒子更新之后，以一定概率重新初始化粒子，構成了動態化的SAPSO-BP神經網絡。

2 預測數據選取

選用美國比斯坎灣(Miami Biscayne Bay,25°43.9′N，80°9.7′W)的潮汐數據作為驗證預測模型性能的樣本。經驗表明，進行相對較精確的潮汐預報，需要對潮位數據進行長時間的觀測和采樣，并對其進行仿真訓練。本文選取了2020年6月1日GMT0000至2020年7月30日GMT2300，共60 d的港口實測潮汐數據進行仿真試驗，實測數據值每隔1 h取樣一次，所以觀測數據共1 440組，將數據列出可得到該時段的潮位時間序列，另外數據集還包括與時間對應的其他非線性氣象因素數據(風速、風向、陣風速、氣溫、氣壓)，以上數據皆可通過NOAA網站(https://tidesandcurrents.noaa.gov/)查詢并下載。其中前1 200組數據用于調和分析及神經網絡的仿真訓練，后240組數據則用于仿真預測。由圖4可見，實測潮位雖有一定周期性，但周期之間的差距較大，由于理論計算過程中只考慮了天體引力以及地球自轉等線性因素，在實際觀測中，存在許多影響潮位的非線性因素，如風、浪、流以及人類活動等對潮位造成的隨機影響，另外，受季節影響的海平面變化及全球氣候變化等因素的影響也會導致實測潮位的不確定波動。

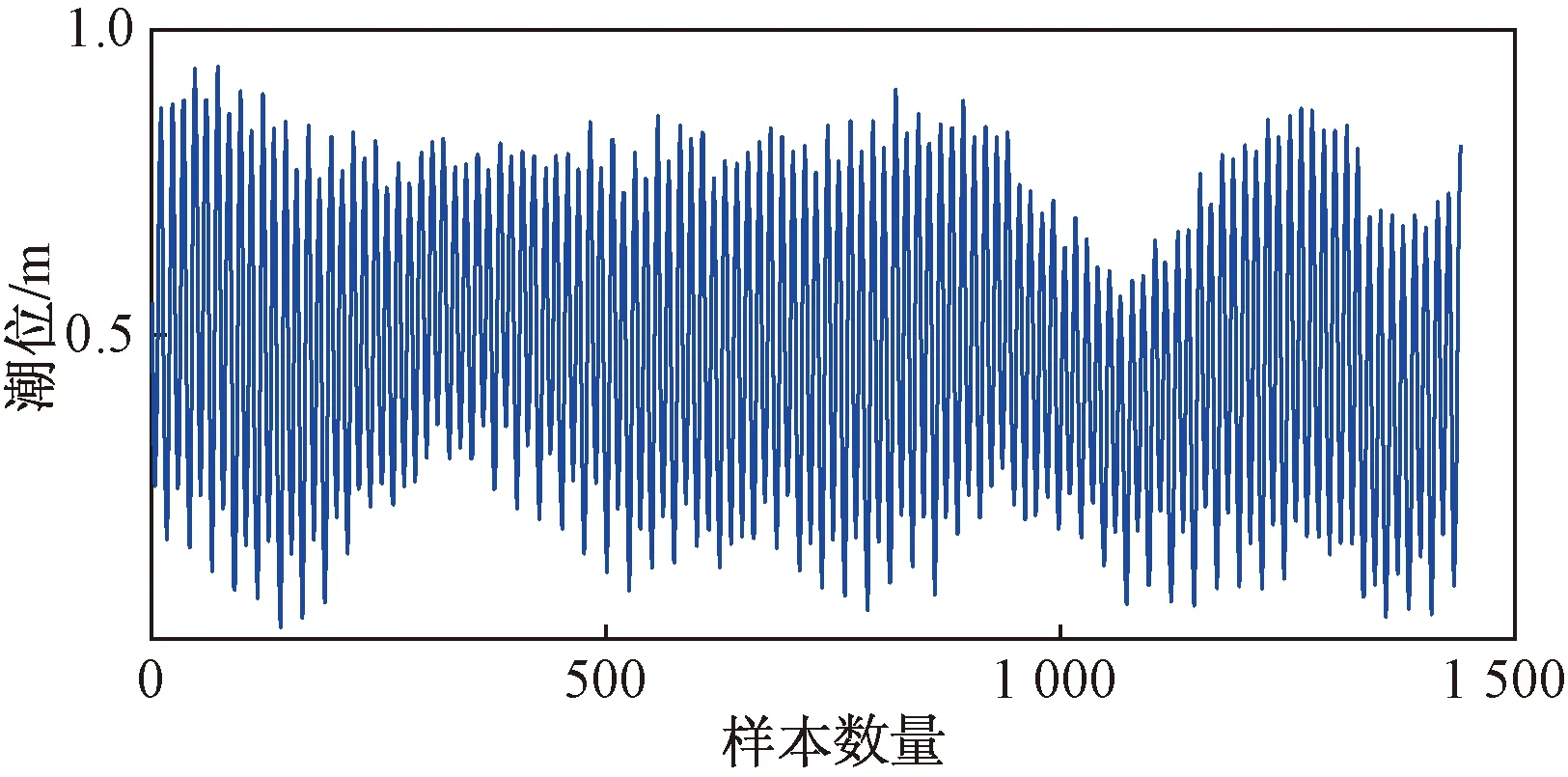
圖4 潮位實測數據Fig.4 The tide level observation data

為了更加直觀地對預測數據進行對比，引入了平均絕對誤差MAE(mean absolute error)，均方誤差MSE(mean square error)及均方根誤差RMSE(root mean square error)三個指標作為判斷預測效果的主要依據。

MAE是預測誤差的絕對值的平均，能更好地反映潮位預測值誤差的實際情況， 計算公式為

(7)

式(7)中：xi為第i個數據的預測誤差。

MSE是指參數估計值與參數真值之差平方的期望值，可以評價數據的變化程度，在誤差對比分析中，其值越小，說明模型預測潮位數據具有更高的精確度，計算公式為

(8)

RMSE是均方誤差的算術平方根，計算公式為

(9)

式中：n為數據個體數。

3 潮位預測仿真及分析

3.1 NARX神經網絡預測分析

在預測之前，需要對NARX神經網絡的輸入初始參數進行設定，其主要內容包括NARX神經網絡的輸入層節點數、隱藏層節點數、輸出層節點數及時延階數，等等。針對NARX神經網絡輸入層的設置與BP神經網絡不同是因為 NARX模型為動態神經網絡，善于通過分析動態數據來擬合物理模型，且能夠儲存之前時刻的記憶，對于非線性擬合有著更強的映射能力，所以針對影響潮位數據的眾多非線性因素，包括風速、風向、陣風速、氣溫、氣壓共5組輸入參數，每一時刻的輸入數據為包含5組參數的元胞(cell)數組，所以此NARX神經網絡預測模型即輸入節點個數為5，輸出層節點個數為1，隱含層的神經元個數由于沒有針對性的公式，所以采取了多次模擬實驗，通過比較帶入不同隱含層神經網絡的預測效果來確定最終輸入的值，結果表明隱含層節點取10時，NARX模型效果最好。輸入和輸出的時延階數按潮汐周期設定為12，運行預測模型，最終得出的預測結果如圖5所示。

圖5 NARX神經網絡預測結果Fig.5 The NARX neural network prediction result

由圖5可見，預測結果基本與實際潮位數據保持一致，只有在潮位峰值以及谷值前后這種變化量較大的時刻，預測誤差相對較大，但對數據整體精確度影響不大。

3.2 MS-NARX神經網絡預測分析

MS-NARX神經網絡在傳統NARX的基礎上引入了模塊化調和分析以及滑動時間窗方法，輸入數據集不變，將輸出數據集替換為非天文潮位數據。輸入和輸出的延時階數根據滑動時間窗長度確定，滑動時間窗是一種用于時間序列操作的重要用法，是使用滑窗(sliding window)來對時間序列進行統計值計算和其他一些函數計算，對于消除噪聲或有缺陷的數據效果顯著，為了確定時間窗口的長度，引入了相關性分析的概念，選用前1 200組潮汐的實測數據計算數據的自相關性值，與t時刻相鄰的不同時刻觀測數據和t時刻觀測數據的相關性由自相關標準值限定，自相關標準值取值較小可以得到更多的相鄰時刻觀測數據，進而可以得到更精確的結果。因此選取0.09自相關值為標準來決定模型的輸入結構，由分析得出，在時間t時刻的數據與其前12 h的數據具有較大的相關性，所以在模型中時間窗長度(window) 及時延階數為12，表示下一個輸出層的模擬數據參考了前12個輸入層的數據，并根據時間步長移動數據窗口。將設置好的參數帶入MS-NARX神經網絡，在MATLAB環境中運行，得到的MS-NARX神經網絡預測結果如圖6所示。

圖6 MS-NARX神經網絡預測結果Fig.6 MS-NARX neural network predictionresult

較于傳統NARX神經網絡，MS-NARX在預測精度及穩定度上有了進一步提升，由誤差數據可見誤差基本穩定保持在±6 cm以內。由于引入滑動時間窗，可以在不增加累計誤差的前提下儲存之前時刻的記憶并將其運用在之后的預測中，同時對輸入數據的模塊化處理又使得MS-NARX神經網絡可以針對復雜的氣候變化對潮位做出更加準確的預測。

3.3 SAPSO-BP神經網絡預測分析

為了完成潮位預測，需要對神經網絡的輸入初始參數進行設定，其主要內容包括神經網絡的層數、對應的輸入層節點數、隱藏層節點數、輸出層節點數及粒子群優化算法的初始參數，等等。

(1)采用經典的三層BP神經網絡。

(2)輸入層的節點數由輸入參數的數量決定。在尋找最優方案過程中，曾采用輸入非線性氣象因素數據的方法進行模型預測，輸入層節點取5(風速、風向、陣風速、氣溫、氣壓)，但在該次實驗中所得預測輸出與實際數據偏差過大，二者相關性R=0.56，預測誤差在±0.4 m之間波動，無法準確對潮位數據做出預測，出現這種情況是因為首先該站點缺乏長時間的系統觀測，只通過即時數據難以表現出其規律；其次，氣象數據對于潮汐的影響是一種復雜的映射關系，單獨將其納入BP神經網絡的結構作為輸入得不到精確的預測結果。為了解決這個問題，采用以調和分析數據作為輸入，最終確定輸入層節點數取12。

(3)隱藏層節點數主要影響BP神經網絡的性能，選取的隱藏層節點數過大或過小，神經網絡預測輸出數據的精度都很難達到預期，所以采用如下經驗公式，即

(10)

式(10)中：M為隱藏層節點數；m為輸入層節點數；n為輸出層節點數；a為0～10的一個隨機自然數。通過經驗公式的計算結合多次試驗預測結果對比，最終確定隱藏層節點數為10個。

(4)對于使用的BP神經網絡模型而言，輸出數據為某一時刻的預測潮位，因此輸出層節點個數設為1個。

(5)SAPSO優化算法的參數：學習因子c1=c2=1.55，迭代次數設為 200，種群規模設為 20，每個粒子的初始速度設置為[-3，3]，每個粒子的初始位置設置為[-5，5]。

本次預測以前1 200組數據進行訓練，后240組數據作為預測輸出。得到的預測潮位與實際潮位數值對比圖如圖7所示。

圖7 SAPSO-BP 神經網絡預測結果Fig.7 SAPSO-BP neural network prediction result

4 預測結果對比及分析

分別針對三種模型的預測輸出及預測誤差進行了對比分析，預測輸出對比圖及誤差對比圖如圖8和圖9所示。

圖8 三種模型預測輸出對比Fig.8 Comparison of prediction results of three models

圖9 誤差對比Fig.9 Comparison of errors

由圖8和圖9可見，優化后的BP神經網絡在時間序列預測上仍不如動態神經網絡，而相比于傳統NARX神經網絡，MS-NARX在潮位預測精確度上又有所提升。SAPSO-BP在BP神經網絡基礎上添加了兩種優化手段，但作為靜態神經網絡不能對時間序列整體的周期性變化及時作出反應，從誤差圖像也能看出，在預測后半部分數據時誤差增大，對于潮位峰值前后的大幅改變，傳統NARX預測模型通常不能及時對預測結果做出調整，以至于在這些時間點的預測輸出繼續增大，在輸出圖像上形成尖角狀曲線；而對于MS-NARX神經網絡預測模型，預測輸出能夠準確、及時地做出調整，使輸出數據盡可能符合實際數據，在潮位峰值前后的時間段，輸出誤差也只是較其他時間段稍有增大，對整體預測結果幾乎沒有影響，且仿真實驗結果同時驗證了MS-NARX模型的泛化能力和適用性。

另外通過計算并比較三種模型的平均絕對誤差MAE，均方誤差 MSE及均方根誤差RMSE可以更加直觀的對比預測效果。將誤差數據分別代入式(7)～式(9)計算，所得結果如表1所示。

表1 MAE，MSE，RMSE對比Table 1 Comparison of MAE, MSE and RMSE

由表1可知MS-NARX模型的三種誤差明顯最小，說明 MS-NARX 模型的預測輸出在離散性，預測差異程度及誤差波動程度上都要優于傳統NARX和 SAPSO-BP 模型。經計算分析，MS-NARX 預測模型的綜合預報精度相對于傳統NARX神經網絡提高了46.5%，相對于SAPSO-BP 預測模型提高了82.0%。

5 結論

基于 NARX 神經網絡，提出了一種改進的實時潮位預測模型MS-NARX，通過選用美國比斯坎灣2020年6月1日GMT0000至2020年8月25日GMT0900的潮汐觀測數據作為驗證預測模型性能的樣本，與SAPSO-BP神經網絡預測模型及傳統NARX進行對比，試驗并證明了使用 MS-NARX 神經網絡預測潮位的可行性，得到以下結論。

(1)MS-NARX模型在動態神經網絡基礎上進行改進，通過輸入數據的模塊化處理針對非天文潮部分進行預測，且引入滑動時間窗降低誤差。

(2)MS-NARX模型的預測潮位和實際觀測潮位之間的最大誤差穩定在±6 cm，RMSE小于0.02 m，吻合情況明顯要優于傳統方法，體現出較高的精度及魯棒性。

(3)MS-NARX 模型對于非線性擬合有著更強的映射能力，更加適用于復雜時間序列數據的分析預測，而且其結構簡單，易于實現，為潮汐水位的實時預報提供了一種有效途徑。

(4)盡管本文利用取自比斯坎灣的數據集進行預測仿真，但所提出的方法不局限于此類數據集，因此，所提出的模型將適用于為其他區域建立潮汐預報模型甚至可以應用于潮汐預報之外的時間序列預測問題中。