基于PCA-IBAS-ELM的海底多相流管道內(nèi)腐蝕速率預測

駱正山, 李蕾

(西安建筑科技大學管理學院， 西安 710055)

近年來中國海洋油氣資源不斷開發(fā)，海底管道建設持續(xù)增長，混輸管道逐漸成為海底管道主流[1-2]。相比于單向流管道而言，混輸管道能帶來更大的經(jīng)濟效益，但輸送介質(zhì)復雜，極易引發(fā)腐蝕泄漏進而造成環(huán)境和財產(chǎn)損失[3]。因此，有效預測海底多相流管道內(nèi)腐蝕速率具有重大現(xiàn)實意義。

中外學者對海底管道腐蝕開展了大量研究。在管道腐蝕機理及影響因素層面，叢軍等[4]通過X射線對海底管道腐蝕產(chǎn)物進行了衍射分析，結果表明其管道內(nèi)壁主要發(fā)生了CO2腐蝕，并對CO2腐蝕機理進行闡述，但未對其腐蝕影響因素的相關性進行深入研究；馬璐等[5]通過掛片實驗，電感探針，顯微鏡等手段對海底管道內(nèi)腐蝕現(xiàn)狀進行研究，分析了其腐蝕類型及可能存在的腐蝕因子，但未對海管內(nèi)部腐蝕趨勢進行預測；馮勝等[6]對海底混輸管道回收管段進行實驗，實驗結果表明管段內(nèi)腐蝕嚴重，以CO2腐蝕為主，同時伴隨有垢下及細菌腐蝕，但未對CO2這一主要腐蝕因素進行深入分析，腐蝕影響程度有待進一步探討；文獻[7]對由CO2引發(fā)的腐蝕進行研究，但影響規(guī)律結果并不穩(wěn)定，未形成定論。

在管道腐蝕預測層面，隨著機器學習算法的快速發(fā)展，越來越多學者將其應用于腐蝕研究，并取得進展。靳文博等[8]利用廣義回歸神經(jīng)網(wǎng)絡預測了海底腐蝕管道的極限承載力，雖然得到的預測值與計算值吻合程度較好，但該網(wǎng)絡的關鍵性能指標——光滑因子采用人為調(diào)試的方法確定具有局限性，且一定程度上增加了運算時間；張新生等[9]基于馬爾科夫理論構建海底管道剩余壽命預測模型，但海底管道數(shù)據(jù)獲取困難，馬爾科夫預測又對原始數(shù)據(jù)依賴過大，導致使用受限；駱正山等[10]提出使用蝗蟲算法(grasshopper optimization algorithm, GOA)優(yōu)化相關向量機(relevance vector machine, RVM)對海底管道腐蝕速率進行預測，但RVM參數(shù)選擇復雜，核函數(shù)要求嚴格，GOA收斂速度慢，因此組合使用效果不佳； Kamrunnahar等[11]使用神經(jīng)網(wǎng)絡作為數(shù)據(jù)挖掘工具對腐蝕行為進行預測，然而神經(jīng)網(wǎng)絡目標函數(shù)復雜、訓練效率低，預測效果不佳。

綜上所述，目前針對海底管道腐蝕問題研究，大多局限于腐蝕現(xiàn)象、腐蝕類型，對于腐蝕機理及腐蝕因素相關性缺少系統(tǒng)分析，同時現(xiàn)有預測所采用的機器學習算法存在弊端。基于此，現(xiàn)深入分析海底多相流管道內(nèi)腐蝕頻發(fā)的根本原因，對影響腐蝕速率的主要因素進行討論，并提出構建PCA-IBAS-ELM組合模型，通過PCA定量篩選腐蝕因素，針對甲蟲天牛須算法(beetle antennae search，BAS)存在的缺陷進行改進，改進后的IBAS算法用于優(yōu)化極限學習機(ELM)關鍵參數(shù)，最后應用于工程實例以檢驗所組合模型的預測效果。

1 理論基礎

1.1 腐蝕機理及影響因素

海底多相流管道介質(zhì)中含有的CO2是引發(fā)腐蝕的主要原因，CO2遇水形成酸性溶液，與金屬表面接觸產(chǎn)生化學反應，生成金屬鹽沉積[12]。

已有研究表明，溫度、pH、流體流速、壓力、CO2分壓和持液率等是影響腐蝕的主要因素[13]。當溫度在40～60 ℃時，CO2腐蝕速率提升，鋼管表面產(chǎn)生碳酸亞鐵，出現(xiàn)較為嚴重的點蝕、坑蝕，當溫度大于60 ℃時，鋼管表面易形成保護膜[14]，從而減緩腐蝕，在60～70 ℃時，腐蝕達到峰值；酸性條件下，產(chǎn)生的H+加劇陽極反應，腐蝕加速；管道內(nèi)腐蝕速率隨流體流速的增加而提升，流體流速增加導致管道承受的切向力加大，切向力會破壞管道表面形成的保護膜，從而加快腐蝕；壓力對腐蝕速率的影響也較為明顯，壓力增大時，管道內(nèi)腐蝕表面受到的應力加大，同時伴隨化學腐蝕產(chǎn)生，腐蝕加速；CO2分壓對腐蝕速率的影響與溫度有關，當溫度在60 ℃以下時，隨CO2分壓加大腐蝕加快，當溫度在60 ℃以上時，隨CO2分壓加大，管道內(nèi)表面將形成腐蝕產(chǎn)物膜，阻礙腐蝕發(fā)生；在多相流管道中，持液率越大，越容易在管道表面形成水膜，酸性氣體溶解其中，生成酸性介質(zhì)，從而加速腐蝕,持液率越小，管道表面越干燥，腐蝕不易發(fā)生。

1.2 算法原理

(1)主成分分析法。主成分分析(PCA)[15-17]算法是通過對原始數(shù)據(jù)集進行一系列矩陣變換，在信息損失最小的前提下實現(xiàn)降維。其重點是求解協(xié)方差矩陣的特征值及特征向量，根據(jù)特征值對主、次位置進行排序，提取位置靠前的因子作為主因子。算法詳解參見文獻[18]。

(2)極限學習機。極限學習機(ELM)[19-20]是一種簡單易用且高效的單隱層前饋神經(jīng)網(wǎng)絡。該方法的輸入權值w和隱層閾值b隨機設置，輸出權值 通過公式計算得到，在預測過程中只需要調(diào)整隱層神經(jīng)元節(jié)點的數(shù)量，選擇適當?shù)膫鬟f函數(shù)。ELM具有學習速度快，泛化性能好等優(yōu)點。算法詳解參見文獻[21]。

(3)甲蟲天牛須算法。甲蟲天牛須算法(BAS)是一種生物啟發(fā)式智能優(yōu)化算法，其過程是對甲蟲覓食行為的模擬[22-23]。甲蟲通過左右兩須對氣味強弱進行判斷，決定行進方向，逐步接近食物所在位置。BAS具有結構簡單、初始參數(shù)少、收斂速度快等優(yōu)點。算法詳解參見文獻[24]。

2 甲蟲天牛須優(yōu)化算法改進

2.1 拓展種群改進

原始甲蟲天牛須算法(BAS)是單個個體的尋優(yōu)過程，在面對復雜問題時尋優(yōu)能力有限，故將其拓展為種群活動。將k維空間中的天牛群按比例分為搜索者，追隨者和探索者。搜索者搜尋最優(yōu)解，追隨者在其周圍尋找潛在解，探索者全局活動，三者協(xié)作可有效避免系統(tǒng)陷入局部最優(yōu)。改進后的甲蟲群朝向和左、右須位置定義同BAS為

(1)

式(1)中：b為甲蟲朝向；rands為隨機函數(shù)；k為空間維度。

(2)

式(2)中：xrt為天牛右須第t次迭代時的位置坐標；xlt為天牛左須第t次迭代時的位置坐標；xt為天牛第t次迭代時的質(zhì)心坐標；dt為天牛第t次迭代時兩須之間的距離，有dt+1=dt×0.95。

迭代過程由單一甲蟲特定移動方式改進為三個子群體遵循不同軌跡協(xié)作進行。搜索者以式(3)更新位置，即

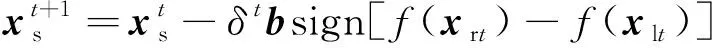
(3)

追隨者在當前最優(yōu)解周圍小范圍移動，尋找潛在解，以式(4)更新位置，即

(4)

探索者以固定的步長隨機移動，以式(5)更新位置，即

(5)

2.2 自適應步長改進

甲蟲行進過程步長迭代的關鍵是步長因子，決定了收斂速度的快慢。原始天牛須算法的步長因子為固定值(0.95)，為了獲得更好的優(yōu)化能力，提出了一種改進動態(tài)步長因子的方法。在優(yōu)化初始階段，為了擴大搜尋范圍，加快尋優(yōu)速度，采用較大步長因子；在優(yōu)化的后期，搜索趨于穩(wěn)定，為了提高解的精度，減小了步進因子。基于以上考慮，作出如下調(diào)整。

(6)

3 模型構建

3.1 PCA-IBAS-ELM模型構建

首先，將腐蝕因素通過主成分分析降維得到主要因素，過程如下。

(1)消除因素之間量綱影響，按式(7)作歸一化處理，即

(7)

(2)歸一化數(shù)據(jù)構成矩陣X，矩陣X的協(xié)方差矩陣R計算公式為

(8)

(3)最后計算R的特征值及特征向量，并按式(9)計算貢獻率，按式(10)計算累計貢獻率，累計貢獻率85%以上的因素定為主因素，分為訓練集及測試集。

(9)

式(9)中：ei為單個因素的貢獻率；λi為R的特征值。

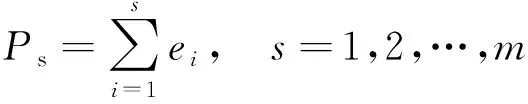
(10)

式(10)中：Ps為各因素累計貢獻率。

其次，將訓練集代入IBAS搜尋最優(yōu)權值閾值，過程如下。

(1)初始參數(shù)設定。選取10個個體組成的天牛群，初始步長δ0為10，最小步長δmin為0.01，兩須初始距離d0為0.05。

(2)種群位置初始化，比較適應度值大小。隨機初始化甲蟲位置，在初始位置對搜索者左右兩須適應度值進行比較,綜合判別最佳行進方向，以式(3)移動，追隨者、探索者遵循2.1節(jié)所講方式協(xié)助尋優(yōu)。

(3)步長更新。迭代完成，將當前最優(yōu)適應度函數(shù)值和歷史最優(yōu)進行比對，根據(jù)比較結果按式(6)更新步長因子。

(4)當適應度值達到預設精度或迭代次數(shù)達到上限，終止運算，輸出最優(yōu)解。

最后，將優(yōu)化后的wj、bj代入ELM，模型目標轉(zhuǎn)為按式(11)計算輸出權值β，進而得到預測值。

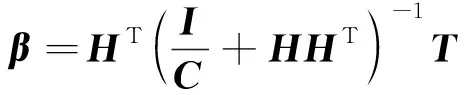
(11)

式(11)中：C為懲罰參數(shù)；H為隱含層輸出矩陣；HT為H的轉(zhuǎn)置；T為輸出矩陣；I為單位矩陣。

在得到輸出權值β后，預測值可表示為

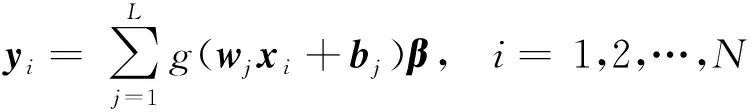
(12)

式(12)中：xi為輸入?yún)?shù)；yi為輸出參數(shù)；wj為輸入權值；bj為隱含層神經(jīng)元閾值；g(x)為激勵函數(shù)；L為隱含層節(jié)點數(shù)；N為任意樣本數(shù)。

3.2 模型驗證指標

選取以下三項指標評價模型性能，即平均絕對誤差(MAE)、平均絕對百分誤差(MAPE)及均方根誤差(RMSE)，與平均誤差相比，平均絕對誤差更能反映預測值誤差的真實情況，均方根誤差可反映出預測的穩(wěn)定性。計算公式為

(13)

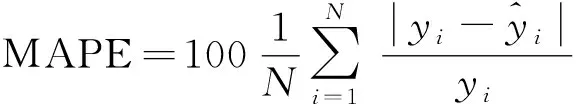
(14)

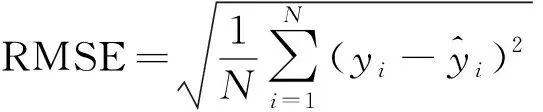
(15)

4 實證分析

4.1 數(shù)據(jù)準備

本文數(shù)據(jù)來自中國海南東部的某海底油氣管道，選取其中50個位置點的腐蝕影響因素及腐蝕速率進行研究，如表1所示。

表1 內(nèi)腐蝕速率及影響因素數(shù)據(jù)Table 1 Internal corrosion rate and influencing factors data

續(xù)表1

4.2 PCA因素提取

根據(jù)PCA算法原理，通過MATLAB軟件，得到上述因素的貢獻率ei及累計貢獻率Ps，如表2所示。

表2 PCA算法處理結果Table 2 PCA processing results

由表2可知，溫度對多相流海底管道內(nèi)腐蝕的影響較大，貢獻率達到38.57%，壓力對其影響較小，貢獻率僅為4.94%。選取累計貢獻率85%以上的因素為主要因素展開下一步研究，即溫度、pH、流體流速和CO2分壓。

4.3 模型訓練

將PCA篩選后的數(shù)據(jù)代入IBAS-ELM模型進行訓練，其中40組為訓練集，10組為測試集。甲蟲種群中的30%、60%、10%分別設為搜索者、追隨者和探索者，最大迭代次數(shù)為200，適應度函數(shù)如式(16)所示，模型激活函數(shù)為Sigmoid函數(shù)如式(17)所示。

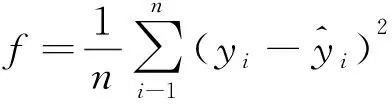
(16)

(17)

迭代過程如圖1所示，由圖1可見IBAS算法尋優(yōu)效果良好，在45次迭代之后趨于穩(wěn)定，此時適應度函數(shù)值為0.033 47。

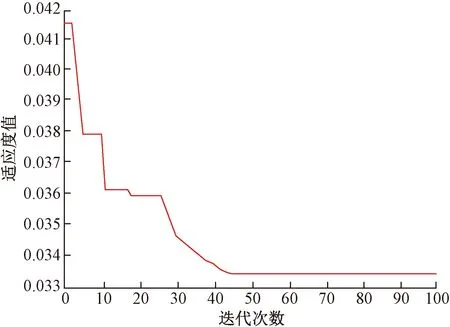
圖1 IBAS-ELM迭代過程Fig.1 IBAS-ELM iterative process

4.4 模型結果對比

將測試數(shù)據(jù)集代入IBAS-ELM模型中，得到預測值，選用BAS-ELM和ELM兩個模型與之對比，結果如圖2所示。分析可知，PCA-IBAS-ELM的預測值與真實值差距較小，擬合效果更佳。

為檢驗模型預測精度，采用相對誤差作為評判標準，對比結果如圖3和表3所示。

圖2 預測結果對比圖Fig.2 Comparison of prediction results

圖3 相對誤差對比圖Fig.3 Comparison of relative errors

結合圖3和表3分析可知， PCA-IBAS-ELM除第5組數(shù)據(jù)外其余誤差均小于其他兩種模型，其相對誤差的平均值為1.132%，低于PCA-BAS-ELM的2.604%和PCA-ELM的6.887%。為進一步評價模型性能，采用3.2節(jié)中的指標對以上3種模型再次對比，結果如表4所示。

由表4可知，PCA-IBAS-ELM模型的MAE、MPAE、RMSE均小于其他兩種模型，三種模型的預測精度從高到低分別為PCA-IBAS-ELM、PCA-BAS-ELM、PCA-ELM，說明采用算法對ELM的輸入權值和隱層閾值進行優(yōu)化可提升預測效果，同時IBAS的優(yōu)化性能高于BAS。

5 結論

提出了以PCA-IBAS-ELM組合模型對海底多相流管道內(nèi)腐蝕速率進行預測，在分析腐蝕機理，介紹模型算法的基礎上，結合中國海南東部某海底油氣管道的50組數(shù)據(jù)實際驗證，得出以下結論。

(1)PCA提取出保留原有樣本信息89.85%的4個關鍵因素，作為ELM的輸入指標，消除了疊加信息的影響，減小了計算壓力，同時采用IBAS對ELM的輸入權值及隱藏層閾值進行優(yōu)化，克服了其隨機設定帶來的不穩(wěn)定性，提高了預測精度。

(2)將PCA-IBAS-ELM與PCA-BAS-ELM進行對比，均方根誤差(RMSE)、平均絕對誤差(MAE)及平均絕對百分誤差(MAPE)分別減小了0.043、0.041、1.513%，表明將單個甲蟲的尋優(yōu)拓展為種群協(xié)作，同時將固定步長因子做自適應改進提升了優(yōu)化算法的性能。

表3 預測相對誤差結果分析Table 3 Analysis of relative error results

表4 模型預測結果性能指標值Table 4 Performance index values of the prediction results