一種基于改進慣性權重的粒子群優化算法*

錢江波 張佳星 姚大偉 李巖 王巧珍

（華北電力大學 保定 071003）

1 引言

粒子群優化（PSO）算法是Kennedy 等［1］提出的一種基于迭代的進化算法。粒子群優化算法具有需要調整的參數少、編程易實現、收斂速度快等優勢，因此被廣泛應用于電力系統中的最優潮流計算、機器人路徑規劃、交通路線規劃等領域［2～5］。

但是粒子群算法也有缺點，當適應度函數比較復雜或參數選擇不合適時，容易陷入局部收斂，其中慣性權重這一參數對算法的收斂性影響最大。慣性權重比較大時，粒子的全局搜索能力較強，此時收斂速度雖然很快，卻不容易得到精確解；慣性權重比較小時，粒子的局部搜索能力強，但是容易陷入局部收斂［5～6］。因此如何尋找一個合適的慣性權重來協調搜索的精度和速度成為當下研究的熱點。

針對上述局限性，姜長元等［8］提出了一種慣性權重正弦調整策略；南杰瓊等［9］提出了一種改進慣性權值的優化策略，在正弦調整的基礎上加入隨機擾動因子調整慣性權值；吳靜等［10］將差分進化算法與余弦函數結合，進而調整慣性權值；趙志剛等［11］提出了一種隨機慣性權重遞減策略；武少華等［12］在簡化PSO 算法的基礎上引入了自適應局部搜索因子，拓寬了搜索范圍并提高了搜索精度；姜建國等［13］提出了一種基于余弦的非線性慣性權重遞減策略。牛仲新等［14］通過把慣性權值設為由粒子位置、個體最優值和全局最優值影響的參數組，使得每個粒子的每一維度都有其對應的慣性權值參數，提高了計算精度。本文提出了一種非線性遞減動態權重策略，并且用四種標準的測試函數作為適應度函數，并與相關文獻中的改進粒子群算法進行對比。結果表明改進后算法不僅在精度上有所提升，穩定性也得到了提高。

2 標準粒子群算法

基本PSO算法是根據鳥群覓食規律提出的，核心思想是隨機初始化一群沒有體積和質量的粒子，把每個粒子看做優化問題的一個可行解，每個粒子在可行解空間內運動，并有一個速度變量決定其方向和距離［15］。在每一次的迭代中，粒子將追隨當前最優的粒子pbest，和群體最優值gbest進行搜索，直到滿足結束條件。標準PSO 算法則是在基本PSO算法的基礎上，通過慣性權重w協調全局搜索和局部搜索能力［7～8］。

式中1 ≤i≤M，c1和c2為學習因子；w為慣性權重；r1和r2為［0-1］范圍內的均勻隨機數；D為搜索空間的維數，1 ≤d≤D；piD和pgD分別為個體極值和全體極值。

其中標準粒子群算法中慣性權重w的計算公式如下：

式中wstart為慣性權重的初始值，一般取0.9；wend為迭代結束的慣性權重值，一般取0.4；t為當前迭代次數；tmax為最大迭代次數。

3 改進權重的粒子群算法

針對標準PSO 算法容易陷入局部最優解導致得到的結果準確性不高，難以達到全局最優，文章結合現有的優化算法提出了一種非線性遞減權重方法，能夠有效平衡局部搜索和全局搜索能力，表示為

式中wstart、wend、t、tmax的含義同式（3），文章中與其他改進粒子群算法作比較時，取ωstart=0.9，ωend=0.4，tmax=1000。同標準粒子群算法中的線性遞減權重相比，改進的慣性權重在迭代初期下降緩慢，從而保持了較好的全局搜索能力，不易陷入局部最優解。在迭代后期慣性權重能夠較快的降低，從而保持了算法的局部搜索能力。

改進算法的實現步驟：

1）初始化。設定初始參數，包括最大迭代次數，學習因子，慣性權重的最大值最小值，種群維數和規模；初始化的隨機位置xi和速度vi，并且將當前位置記為每個粒子的pi，從所有個體極值中找出全體極值，記為pg。

2）評價粒子。計算粒子的適應度值，如果優于當前個體極值，則將pi設置為該粒子的位置。如果所有個體極值中最優解優于當前的全局極值，則將pg設置為該粒子的位置。

3）粒子的更新。根據式（1）和式（2）更新粒子的速度與位置，當速度超過設定的邊界值時取邊界值。

4）檢驗是否符合結束條件。如果當前的迭代次數達到了設定值，或適應度值的增量小于預定的值，則停止迭代，否則跳轉步驟2）。

4 仿真驗證

為了驗證改進后算法的性能，選用了四個標準的測試函數進行檢驗［16］，并與文獻［9］和文獻［13］的改進算法進行對比。基本參數設置為：c1、c2均取2，種群數量PopSize取40，種群維數取30，最大迭代次數為500次。

四個測試函數如下：

1）F1：Sphere函數

該函數是非線性的、對稱的單峰函數。該函數的全局最優點的函數值F1(x)=0。

2）F2：Rosenbrock函數

該函數是一個單峰函數，函數變量之間具有很強的相關性，且函數的搜索方向容易受梯度信息的誤導，不易找到全局最優。該函數的全局最優點的函數值F2(x)=0。

3）F3：Rastrigin函數

該函數為多峰函數，此函數增加了一個余弦函數來產生大量的最優點。因此在計算時容易陷入局部最優。該函數的全局最優點的函數值F3(x)=0。

4）F4：Griewank 函數

該函數為多峰函數，存在很多局部最小點。由于變量之間具有顯著的相關性，因此算法在計算時容易陷入局部最優。該函數的全局最優點的函數F4(x)=0。

對以上四個函數分別用三種不同的算法各運行50 次，并記錄不同方法所對應的最大值、最小值、平均值和方差，結果如表1所示。

表1 函數測試結果

為了能更加直觀地看到對比情況，用Matlab軟件將四種函數分別用三種不同算法得到的的最優值變化曲線畫出來，如圖1～4所示。

圖1 Sphere函數最優值變化趨勢

從表1 可以看出，用本文的改進方法后測試函數F1、F2、F3和F4的最優值相對于文獻［9］和文獻［13］的改進算法在精確度上有著明顯的提升，更加接近真實值，平均值均有較為明顯的下降，且方差也均有明顯下降，說明改進后算法的穩定性有著進一步提高。并且同其他兩種改進粒子群算法相比，用本文改進后的粒子群算法發現四個測試函數的均值和方差結果相似，誤差相對較小，證明了改進是有意義的。

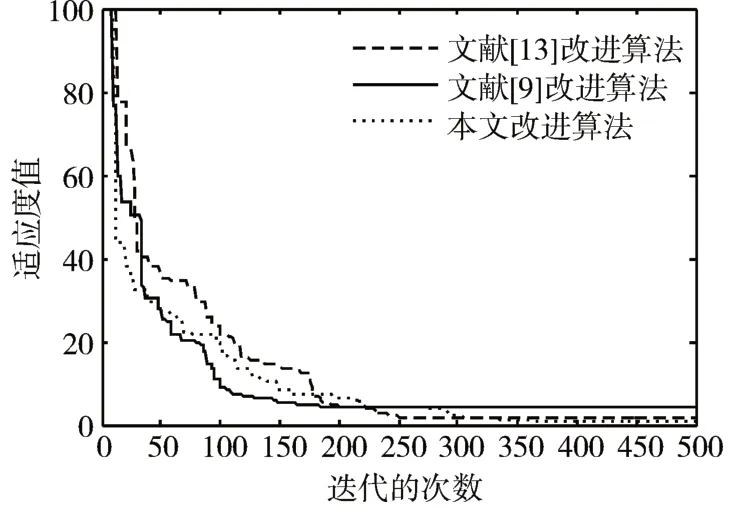
圖2 Rosenbrock函數最優值變化趨勢

圖3 Rastrigin函數最優值變化趨勢

圖4 Griewank函數最優值變化趨勢

通過圖1～4 可以看出，本文的改進算法在計算后期曲線有著階梯狀彎曲下降，說明能夠在后期更好的避免早熟現象，從而跳出局部收斂。同時通過對圖1～3 的觀察發現，對于Sphere、Rosenbrock 和Rastrigin 函數文獻［9］和文獻［13］的收斂時間早于本文改進算法，說明在收斂時間上有待改善。

5 結語

本文通過對標準粒子群算法和其他兩種改進粒子群算法的分析，提出了一種新的慣性權重遞減策略，并且通過對四種標準測試函數的仿真實驗，可以看出提出的改進算法較其他兩種算法具有更高的計算精度，較好的算法穩定性。能夠更好地跳出局部最優點，避免早熟，計算結果更加接近真實值，具有較好的效果。