一種基于小生境的自適應(yīng)入侵野草優(yōu)化算法*

馬躍 杜先君 程生毅

（蘭州理工大學(xué)電氣工程與信息工程學(xué)院 蘭州 730050）

1 引言

自遺傳算法提出以來(lái)，智能算法的發(fā)展如火如荼，成為了人工智能技術(shù)最為活躍的分支之一。粒子群優(yōu)化［1］、蟻群算法［2］、布谷鳥搜索算法［3］和蝙蝠算法［4］等受各種生物習(xí)性所啟發(fā)的元啟發(fā)式智能算法先后被提出。這些算法作為強(qiáng)有力的數(shù)值優(yōu)化工具，被廣泛用于模式識(shí)別［5］、系統(tǒng)辨識(shí)［6］、參數(shù)估計(jì)［7～8］和故障診斷［9］等領(lǐng)域。

小生境思想起源于生物學(xué)概念，最早用于遺傳算法中，顯著提高了遺傳算法的全局收斂能力和收斂速度。小生境思想可以根據(jù)不同的判斷標(biāo)準(zhǔn)，將遺傳算法的種群劃分為若干類，能顯著提高算法的種群多樣性。

入侵野草優(yōu)化（IWO）算法是一種新型的智能優(yōu)化算法，于2006 年由Mehrabian 等提出［10］。IWO通過模仿田間雜草的生長(zhǎng)、繁殖、擴(kuò)散和競(jìng)爭(zhēng)的繁衍習(xí)性，模擬了野草強(qiáng)大的殖民統(tǒng)治能力，已經(jīng)被廣泛應(yīng)用于工程優(yōu)化［11～12］、故障診斷［13］和算法混合優(yōu)化［14］等領(lǐng)域。在IWO 算法中，隨著迭代次數(shù)的增加，產(chǎn)生下一代種子的空間分布范圍會(huì)逐步縮小，這樣可以保證算法前期具有較強(qiáng)的全局搜索能力，而后期則有較強(qiáng)的局部搜索能力。然而，這也導(dǎo)致了算法在前期的局部搜索能力不足，后期又會(huì)缺乏種群多樣性。為了獲得更好的優(yōu)化效果，有必要對(duì)標(biāo)準(zhǔn)IWO 算法進(jìn)行適當(dāng)?shù)母倪M(jìn)和融合。Cuevas 等［14］提出了一種混合進(jìn)化方法，該方法將IWO與估計(jì)分布算法相結(jié)合，結(jié)合了IWO 的搜索能力和估計(jì)分布算法的概率模型，使得產(chǎn)生的混合方法具有更高的精度、效率和魯棒性。LIU 等［12］在IWO算法中引入簡(jiǎn)化二次逼近，在陣列天線的方向圖合成方面的應(yīng)用顯示了對(duì)IWO算法改進(jìn)的有效性。

針對(duì)上述缺陷，本文將小生境思想和自適應(yīng)機(jī)制引入IWO 算法中，提出一種基于小生境思想的自適應(yīng)野草入侵算法（NAIWO）。小生境思想用來(lái)增加算法的種群多樣性；自適應(yīng)機(jī)制中引入周期算子和自適應(yīng)算法，使野草個(gè)體的空間擴(kuò)散的標(biāo)準(zhǔn)差不僅隨迭代次數(shù)變化，而且可以根據(jù)周期算子的參數(shù)和個(gè)體的適應(yīng)度值來(lái)動(dòng)態(tài)變化。在對(duì)多個(gè)測(cè)試函數(shù)的尋優(yōu)過程中，表明了NAIWO 算法在收斂能力和收斂速度方面的優(yōu)勢(shì)。

2 入侵野草優(yōu)化

IWO 算法［10］模仿田間雜草擴(kuò)散、生長(zhǎng)、繁殖和競(jìng)爭(zhēng)性生存的基本過程，‘野草’表示所求問題的一個(gè)可行解，‘種群’表示所有野草個(gè)體的集合。

IWO算法的基本步驟可以表示如下：

1）種群初始化。在解空間（D 維）上隨機(jī)產(chǎn)生P0個(gè)野草（可行解）。通常可根據(jù)實(shí)際情況調(diào)整P0的大小。

2）生長(zhǎng)繁殖。種子生長(zhǎng)、開花后分別根據(jù)自己的適應(yīng)度產(chǎn)生新一代的種子，父代所產(chǎn)生的種子數(shù)量與父代的適應(yīng)度有關(guān)。具體關(guān)系如式（1）所示：

式中，F(xiàn)N和SN分別表示第N個(gè)父代的適應(yīng)度值和其應(yīng)產(chǎn)生的種子數(shù)；Fmax和Fmin分別表示父代中的最大、最小適應(yīng)度；Smax、Smin分別表示野草個(gè)體產(chǎn)生種子數(shù)目的最大、最小值。產(chǎn)生的種子數(shù)為SN向下取整。

3）空間擴(kuò)散。產(chǎn)生的種子按正態(tài)分布在其父輩附近的D 維空間中。該正態(tài)分布的均值為0，標(biāo)準(zhǔn)差為σiter。其中標(biāo)準(zhǔn)差隨迭代次數(shù)的變化如公式（2）所示：

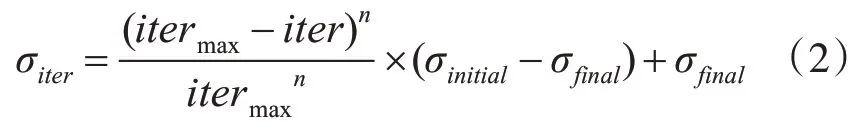
式中，iter 和itermax表示當(dāng)前迭代次數(shù)和最大迭代次數(shù)；σinitial表示起始標(biāo)準(zhǔn)差值，σfinal表示最終標(biāo)準(zhǔn)差值；n 表示非線性調(diào)和系數(shù)。一般保證σfinal大于σfinal。

4）競(jìng)爭(zhēng)排斥。若干代的繁殖后，環(huán)境資源將無(wú)法承受產(chǎn)生的后代數(shù)目，將最大種群大小確定為預(yù)先設(shè)定的最大種群數(shù)目Pmax，達(dá)到Pmax時(shí)先按之前步驟自由繁殖，然后以種群上限要求為標(biāo)準(zhǔn)，將父代和子代一起按適應(yīng)值大小進(jìn)行淘汰。

5）重復(fù)步驟2）至4），直到達(dá)到最大迭代次數(shù)或者找到滿足條件的解。

3 基于小生境的自適應(yīng)野草入侵優(yōu)化

由式（1）和式（2）可知，在標(biāo)準(zhǔn)IWO 算法中，每一代的野草個(gè)體根據(jù)適應(yīng)度大小決定產(chǎn)生下一代的數(shù)量，這樣就可以保證把優(yōu)良的個(gè)體基因遺傳給下一代。并且隨著迭代的進(jìn)行，產(chǎn)生下一代種子的擴(kuò)散范圍（即標(biāo)準(zhǔn)差σiter的大小）逐漸減小，這樣就保證了算法在前期具有較強(qiáng)的全局搜索能力，后期也有較強(qiáng)的局部尋優(yōu)能力。但是這樣也同樣導(dǎo)致了算法前期的局部搜索能力不足，而后期只在適應(yīng)度較高的種子附近搜索，導(dǎo)致算法后期缺乏多樣性。針對(duì)上述問題，本文引入小生境思想和自適應(yīng)機(jī)制，提出一種基于小生境的自適應(yīng)入侵野草優(yōu)化算法（Niche based Adaptive Invasive Weed Optimization，NAIWO）。

3.1 動(dòng)態(tài)自適應(yīng)機(jī)制

在標(biāo)準(zhǔn)IWO 算法步驟3）中，每一個(gè)父代所產(chǎn)生的下一代種子的分布服從同一個(gè)正態(tài)分布，其散步標(biāo)準(zhǔn)差為σiter，σiter是隨迭代次數(shù)而減小的。這種分布方法雖然考慮了迭代前期的全局搜索和后期的局部搜索能力，但也會(huì)導(dǎo)致算法后期的種群多樣性不足，使算法容易陷入局部最優(yōu)。本文引入動(dòng)態(tài)自適應(yīng)機(jī)制到標(biāo)準(zhǔn)IWO 算法的空間擴(kuò)散步驟中，來(lái)平衡算法的全局和局部尋優(yōu)能力。

在動(dòng)態(tài)自適應(yīng)空間擴(kuò)散機(jī)制中，每一個(gè)父代產(chǎn)生的子代的空間分布σj如式（4）和式（5）所示。在式（4）中引入了余弦周期函數(shù)，T 為周期參數(shù)，K 為伸縮因子。通過調(diào)整K 和T 值的大小可以調(diào)整動(dòng)態(tài)擴(kuò)散標(biāo)準(zhǔn)差σiter在［1/K，K］之間以周期T 變化。對(duì)于第j 個(gè)父代‘野草’，其產(chǎn)生的子代分布情況σj還與其在種群中的適應(yīng)度大小有關(guān)，如式（5）所示。在每一次迭代中，F(xiàn)max、Fmin為父代種群的中的最大、最小適應(yīng)度值；Fj為第j 個(gè)父代的適應(yīng)度值。每一代種群的分布情況不僅與迭代次數(shù)iter 有關(guān)，還會(huì)與父代在種群中的適應(yīng)度大小呈現(xiàn)函數(shù)關(guān)系。在迭代過程中，適應(yīng)度越高的野草，產(chǎn)生的下一代種子的數(shù)量也越多，而其下一代的分布也更加集中，使得種子不斷向高適應(yīng)度集中；而適應(yīng)度低的父代，產(chǎn)生的種子數(shù)也較少，但其分布范圍反而更大，使其能搜索更大的范圍，從而提高發(fā)現(xiàn)全局最優(yōu)解得可能。

3.2 小生境思想

小生境思想來(lái)源于生物學(xué)，是指特定環(huán)境下的一種生存環(huán)境，生物在其進(jìn)化過程中，一般總是與自己相同的物種生活在一起，共同繁衍后代。將每一代個(gè)體按適應(yīng)度值劃分為若干類，每一個(gè)類都可以代表一個(gè)小生境。小生境思想與智能算法的結(jié)合的過程中顯示了強(qiáng)大的效用［15～16］。本文中將小生境思想引入IWO 算法的競(jìng)爭(zhēng)排斥步驟中，借助小生境的分類競(jìng)爭(zhēng)特點(diǎn)進(jìn)行種群繁殖，以此來(lái)增加種群多樣性，提高算法的全局尋優(yōu)能力。小生境的半徑R的確定以式（6）為依據(jù)：

式（6）中，dni表示第iter次迭代中，第i個(gè)野草到適應(yīng)度最高的野草之間的歐式距離。a、b 和k 為可調(diào)整參數(shù)，調(diào)整其值可以相應(yīng)調(diào)整小生境的半徑R的變化速率和始、終值。

劃分小生境的過程表述如下：

1）根據(jù)適應(yīng)度的大小，對(duì)種群中的野草個(gè)體進(jìn)行降序排列。若種群數(shù)量大于最大種群數(shù)目Pmax，則取前Pmax個(gè)野草個(gè)體。

2）以適應(yīng)度最高的野草為第一個(gè)小生境的H1中心，R 為其半徑。若種群中的其他個(gè)體距離小生境H1的中心的歐氏距離d1i小于R，則其屬于小生境H1。反之，則不屬于。

3）以不屬于小生境H1的其余個(gè)體中適應(yīng)度最高的的野草為中心，標(biāo)記第二個(gè)小生境H2。方法同2）。以此類推，直到種群中所有個(gè)體都被標(biāo)記。

基于小生境的自適應(yīng)野草入侵算法（NAIWO）的步驟可描述如下：

步驟1）：種群和參數(shù)初始化。

步驟2）：計(jì)算各個(gè)野草個(gè)體的適應(yīng)度，按上述小生境分類方法對(duì)各個(gè)野草個(gè)體劃分小生境。

步驟3）：對(duì)于各小生境內(nèi)的個(gè)體，根據(jù)方程（1）的方法生長(zhǎng)繁殖，產(chǎn)生種子。

步驟4）：按照方程（3）、（4）和（5）進(jìn)行根據(jù)適應(yīng)度的自適應(yīng)空間擴(kuò)散。

步驟5）：判斷是否找到符合要求的解，若是，則結(jié)束，輸出最優(yōu)解；若否，則繼續(xù)。

步驟6）：判斷是否達(dá)到最大迭代次數(shù)。若是，則結(jié)束，輸出最優(yōu)解；若否，則繼續(xù)。

步驟7）：判斷當(dāng)前野草個(gè)體數(shù)Piter是否大于最大種群數(shù)Pmax，若是，則繼續(xù)；若否，轉(zhuǎn)至步驟2）。

步驟8）：競(jìng)爭(zhēng)排斥。從每個(gè)小生境中挑選出一定數(shù)量的野草個(gè)體，作為父代進(jìn)入下一次迭代。每個(gè)小生境中挑選的作為的個(gè)體數(shù)量與小生境中的個(gè)體數(shù)量占種群個(gè)體總數(shù)的比值有關(guān)。如式（7）所示：

Pmax為設(shè)定的最大種群數(shù)量，X（i）表示第i 個(gè)小生境中的個(gè)體數(shù)量，sum（X）為所有小生境個(gè)體數(shù)量之和。

步驟9）：重復(fù)步驟2）至步驟8），直到找到最優(yōu)解或達(dá)到最大迭代次數(shù)。

4 仿真實(shí)驗(yàn)

為了評(píng)估所提出的NAIWO 算法的優(yōu)化性能，本節(jié)設(shè)計(jì)了兩部分仿真實(shí)驗(yàn)。第一部分通過尋找3個(gè)2維數(shù)學(xué)基準(zhǔn)函數(shù)的全局最小值來(lái)對(duì)比IWO和NAIWO 算法的尋優(yōu)效果。第二部分測(cè)試對(duì)3 個(gè)更高維度的數(shù)學(xué)基準(zhǔn)函數(shù)的尋優(yōu)效果，并與遺傳算法（GA），蝙蝠算法（BA）和IWO 進(jìn)行對(duì)比。這些數(shù)學(xué)基準(zhǔn)函數(shù)被廣泛應(yīng)用于新提出的智能算法或其改進(jìn)算法的性能測(cè)試中［17～18］，其基本信息如表1所示。

表1 數(shù)學(xué)基準(zhǔn)函數(shù)信息

在第一部分仿真時(shí)，IWO 算法和NAIWO 算法的初始搜索范圍σinitial一般為xi定義域的1%，最終搜索范圍σfinal=1e-5；初始種群數(shù)量P0=25，最大種群數(shù)量Pmax=100；最大迭代次數(shù)itermax=300；在NAIWO 算法中，小生境的半徑的確定參數(shù)a=3，b=1.05，k=0.6；自適應(yīng)空間擴(kuò)散參數(shù)K=5，周期T=10。

圖1 顯示了在對(duì)每個(gè)基準(zhǔn)函數(shù)進(jìn)行尋優(yōu)測(cè)試時(shí)，兩種算法的適應(yīng)度曲線。在測(cè)試時(shí)，選擇的最大迭代次數(shù)為300，而兩種算法的全局搜索則主要體現(xiàn)在前100 代，后邊的迭代過程主要是局部搜索以便獲得更好的收斂精度。故在生成適應(yīng)度曲線時(shí)，為了更好地顯示對(duì)比性，選擇前100 代的數(shù)據(jù)。圖1 的3 個(gè)曲線顯示了相對(duì)于IWO 算法，本文提出的NAIWO算法不管是全局收斂能力還是收斂速度上都有明顯的優(yōu)勢(shì)。

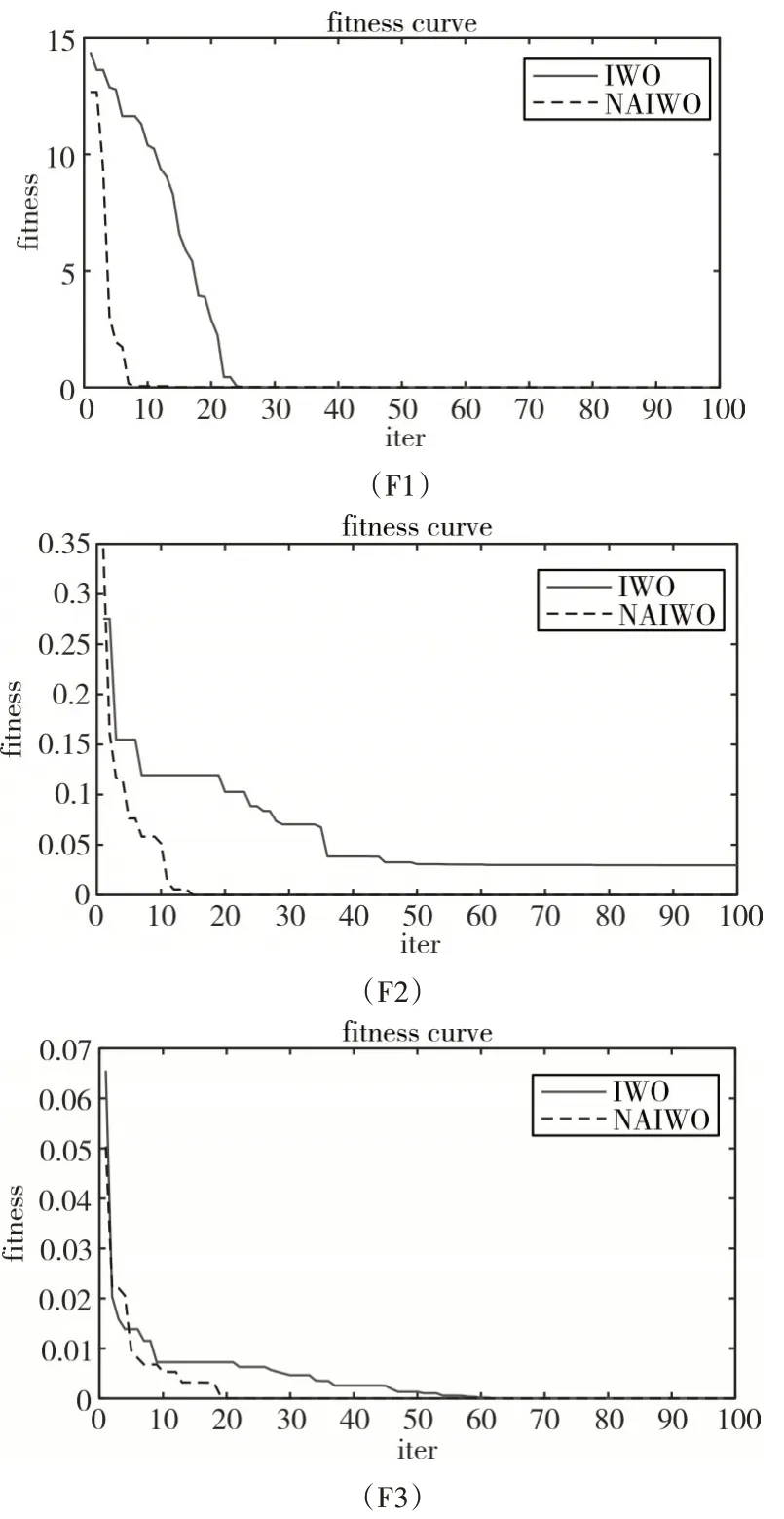
圖1 IWO和NAIWO的適應(yīng)度曲線

為了獲得更公允的數(shù)據(jù)，對(duì)每個(gè)函數(shù)都進(jìn)行30 次測(cè)試，分別計(jì)算每個(gè)函數(shù)測(cè)試的收斂結(jié)果的平均值，最小值和30次測(cè)試的方差，如表2所示。

對(duì)比表2 中兩種算法的最小收斂值，可以看出在多數(shù)情況下，NAIWO 算法比IWO 算法具有相當(dāng)或者更高的收斂精度。與此同時(shí)，收斂均值則更能反應(yīng)算法的總體收斂情況，這個(gè)指標(biāo)的運(yùn)行數(shù)據(jù)反映了相比于IWO，NAIWO 具有更高的收斂概率。方差數(shù)據(jù)則體現(xiàn)了兩種算法的穩(wěn)定性，這一組數(shù)據(jù)的對(duì)比顯示NAIWO算法收斂到全局最優(yōu)解的穩(wěn)定性遠(yuǎn)高于IWO。

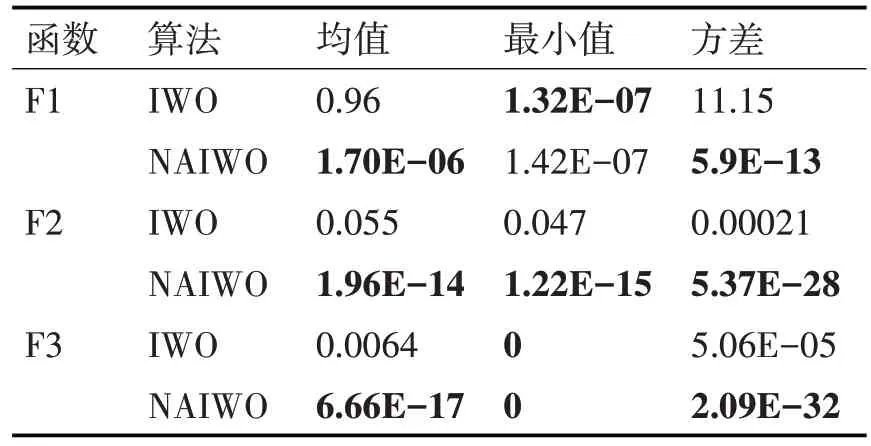
表2 IWO和NAIWO的統(tǒng)計(jì)學(xué)數(shù)據(jù)對(duì)比

為了進(jìn)一步驗(yàn)證所提出NAIWO算法的尋優(yōu)能力，以及對(duì)比其他智能算法的優(yōu)越性，在第二部分測(cè)試中，加入了GA 和BA 兩種著名的優(yōu)化算法，對(duì)四種優(yōu)化算法的優(yōu)化能力進(jìn)行對(duì)比。迭代次數(shù)為500，其他參數(shù)值選取方法同上。

表3 所示為4 種算法的30 次運(yùn)行的統(tǒng)計(jì)學(xué)數(shù)據(jù)。在對(duì)F4函數(shù)的30次運(yùn)行中，BA算法的最小收斂精度是4 種算法中最高的，但是其收斂的平均值和方差都高于NAIWO 算法一個(gè)或多個(gè)數(shù)量級(jí)，說(shuō)明其收斂概率和穩(wěn)定性遠(yuǎn)不如NAIWO 算法。F4-F6 這3 個(gè)高維函數(shù)的統(tǒng)計(jì)學(xué)數(shù)據(jù)對(duì)比顯示NAIWO 算法在穩(wěn)定性和收斂精度上，相對(duì)于其他三種算法都有較大優(yōu)勢(shì)，再次驗(yàn)證了所提出算法的有效性和優(yōu)越性。

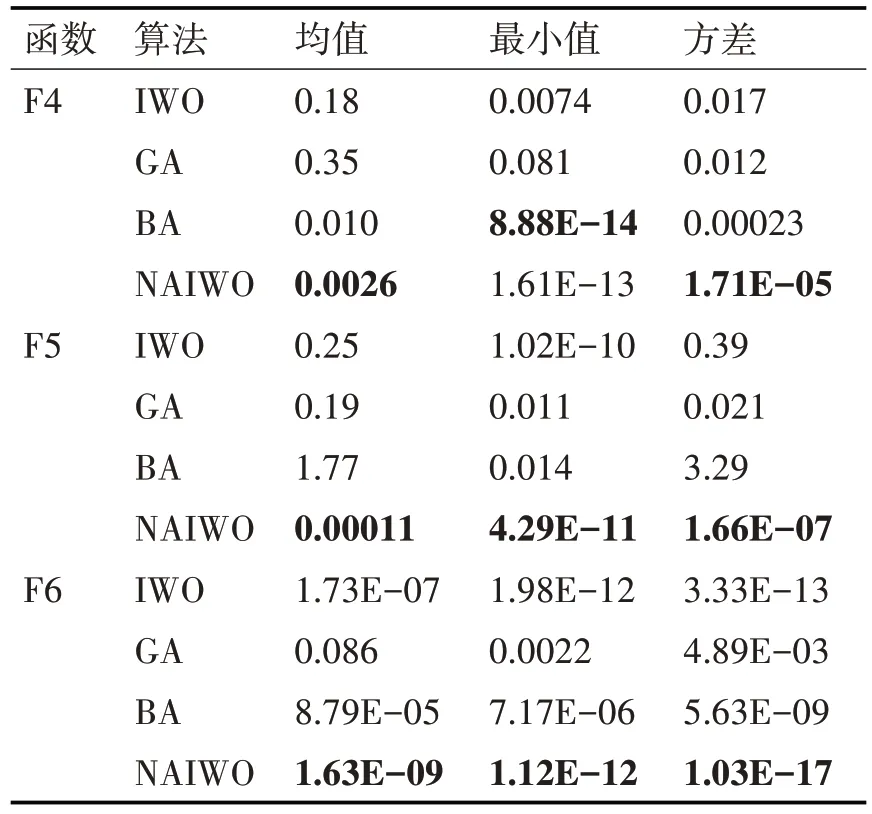
表3 GA、BA、IWO和NAIWO的統(tǒng)計(jì)學(xué)數(shù)據(jù)

5 結(jié)語(yǔ)

本文針對(duì)入侵性野草優(yōu)化（IWO）算法在迭代前期局部搜索能力不足，后期種群多樣性不足等缺點(diǎn)，提出了一種基于小生境的自適應(yīng)入侵性野草優(yōu)化（NAIWO）算法。通過尋找6 個(gè)數(shù)學(xué)基準(zhǔn)測(cè)試函數(shù)的最小值，驗(yàn)證了NAIWO 算法的有效性。與GA、BA 和IWO 算法的對(duì)比顯示了NAIWO 算法在獲得較高的收斂精度的基礎(chǔ)上，做到了算法的全局收斂能力和和收斂速度的均衡，并提高了算法的穩(wěn)定性。