有限域上一類對合多項式的計數

張召輝, 廖群英

(四川師范大學 數學科學學院, 四川 成都 610066)

1 序言及主要結果

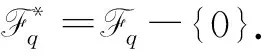
鑒于對合多項式的重要性,目前已經有一部分關于對合多項式的研究.Charpin等[7]在討論偶特征域上的Dickson多項式時,開啟了關于對合多項式顯性表達式及其不動點的研究.自此,人們開始關注這個問題:Charpin等[8]討論了偶特征域上的對合單項式個數以及線性對合多項式;Castro等[9]給出Fq上的單項式在Fq上對合的充要條件,以及具有特定個數不動點的單項式在Fq上對合的充要條件;Fu等[10]證明了目前已知的四差分一致置換多項式中,大部分都不是對合多項式;Zheng等[11]利用分圓多項式的思想給出一類特殊形式的多項式是對合的充要條件;Niu等[12]基于AGW準則給出另一類特殊形式的多項式是對合的充要條件;張召輝等[13]通過討論有限域上兩個對合多項式的不動點集合與非不動點集合之間的關系,給出了兩個對合多項式復合后仍然對合的充要條件等.

本文基于文獻[13]給出的充要條件,在給定對合多項式f(x)∈Fq[x]的情況下,對任意g(x)∈Fq[x],通過討論f(x)與g(x)不動點集合與非不動點集合之間的交集合,確定了使得復合函數f°g(x)和g(x)均對合的g(x)的計數公式.

為方便,記Af表示多項式f(x)∈Fq[x]在Fq中的不動點集合.

引理 1.1[12]設f(x)∈Fq[x]為Fq上的對合多項式,|Af|=n(n∈N),則q-n為偶數.特別地,當q為奇數時,|Af|≤1.

由引理1.1可知,如果f(x)∈Fq[x]為對合多項式,則|Fq-Af|為偶數,不妨設為

|Fq-Af|=2h,h∈N,

而Fq-Af為f(x)在Fq上的非不動點集合,故可設βi=f(αi)(i=1,2,…,h),并以(αi:βi)(i=1,2,…,h)表示2-輪換(即對換).

對Fq中的對合多項式f(x),記

Bf={(α1:β1),…,(αh:βh)};

Mf={g(x)∈Fq[x]|g(x),f°g(x)均為Fq上的對合多項式,|Af∩Ag|=|Af|,Bf?Bg};

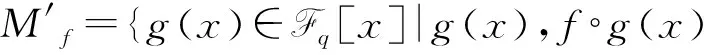
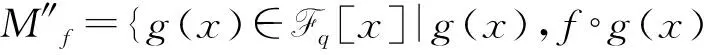
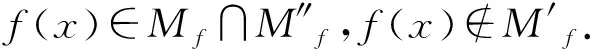
引理 1.2[13]設f1(x),f2(x)∈Fq[x]為Fq上的對合多項式,則f1°f2(x)為Fq上的對合多項式當且僅當對任意x∈Af1,有f2(x)∈Af1,并且對(x:f1(x))∈Bf1,以下條件之一成立:

1)x,f1(x)∈Af2;

2) (x:f1(x))∈Bf2;

3) 存在(x1:x2)∈Bf1,使得(x1:x2)≠(x:f1(x)),且(x:x1),(f1(x):x2)∈Bf2.

本文利用上述充要條件,通過討論Fq上兩個對合多項式f(x)與g(x)的不動點集合與非不動點集合之間的交集合,確定了一類特殊的對合多項式的計數公式,即證明了如下主要結果.

定理 1.3設f(x)∈Fq[x]為Fq上的對合多項式,|Af|=n(n∈N),則:

1)Mf={f(x)},即|Mf|=1;

3)

其中

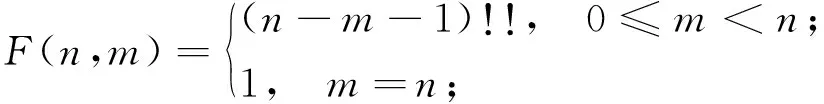
2 主要結果的證明

證明定理1.3.

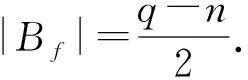
任取g(x)∈Mf,由Bf?Bg可知

|Bf∩Bg|=|B

即Ag?Af.

因為g(x)∈Mf,所以|Af∩Ag|=|Af|,但是Ag?Af,從而|Af|=|Ag|=n,即Af=Ag.

所以，由Af=Ag,Bf=Bg，可知g(x)=f(x),即Mf={f(x)},|Mf|=1.

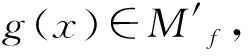
注意到Bf?Bg,所以Ag?Af,從而

m=|Af∩Ag|=|Ag|.

因為f(x)、g(x)和f°g(x)均為Fq上的對合多項式,所以由引理1.2可知，對任意x∈Af,有g(x)∈Af.下面對任意x0∈Af,分以下兩種情形討論.

情形 1 當x0∈Ag時,有g(x0)=x0∈Ag?Af.

情形 2 當x0∈Af-Ag時,由x0?Ag可知g(x0)≠x0.

若g(x0)∈Ag,由g(x0)為Fq上的對合多項式及對合多項式的定義,易得x0∈Ag,此與x0?Ag矛盾,故g(x0)?Ag,即g(x0)∈Af-Ag-{x0}.

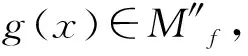
|Af∩Ag|=m, 0≤m≤n,

|Bf∩Bg|=j.

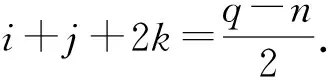
對于任意x0∈Ag,有情形3和4.

情形 3 當x0∈Af時,有x0∈Af∩Ag.

情形 4 當x0∈Fq-Af時,有(x0:f(x0))∈Bf.又x0∈Ag,故由引理1.2中1)可知f(x0)∈Ag.

又Bf中有i個2-輪換滿足引理1.2中的1),|Af|=n,且|Af∩Ag|=m(0≤m≤n),故

|Ag|=m+2i.

再由引理1.1可知q-m-2i和q-n均為偶數,從而n、m與q同奇偶.

對于x0∈Fq-Ag,可知g(x0)≠x0,(x0:g(x0))∈Bg.有情形5和6.

情形 5 當f(x0)=x0時,有x0∈Af,因為x0∈Fq-Ag,所以x0∈Af-Ag,又因為f°g(x)為Fq上的對合多項式,所以由引理1.2可知g(x0)∈Af,而g(x0)≠x0,故g(x0)∈Af-Ag-{x0}.

情形 6 當f(x0)≠x0時,有(x0:f(x0))∈Bf.

(Ⅰ) 若(x0:f(x0))=(x0:g(x0)),則f(x0)=g(x0),從而(x0:f(x0))∈Bf∩Bg.

(Ⅱ) 若(x0:f(x0))≠(x0:g(x0)),因為f°g(x)為Fq上的對合多項式,所以,由引理1.2可知,存在(x1:x2)∈Bf,使得(x1:x2)≠(x0:f(x0)),且(x0:x1),(f(x0):x2)∈Bg.

又Bf中有2k個2-輪換滿足引理1.2中的條件3),故

|B

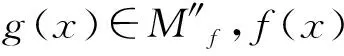
|Af|=n,n∈N, |Af∩Ag|=m,

0≤m≤n, |Bf∩Bg|=j,

且Bf中有i個2-輪換滿足引理1.2中1),2k個2-輪換滿足3),則滿足條件的g(x)的個數為:

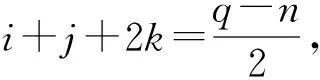
事實上,不妨設

Af={al1,al2,…,alm,alm+1,…aln},

B1={(b1:f(b1)),(b2:f(b2)),…,(bi:f(bi))},

B2={(d1,1:f(d1,1),(d2,1,f(d2,1),…,

(dk,1:f(dk,1)}(當k=0時,B2=?),

B3={(d1,2:f(d1,2)),(d2,2:f(d2,2)),…,

(dk,2:f(dk,2))}(當k=0時,B3=?),

B4={(c1:f(c1)),(c2:f(c2)),…,(cj:f(cj))},

B當k=0時,B

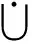
B5={(alm+e:aln+1-e)|1≤e≤n-m-1}

(當n=m時,B5=?).

由拉格朗日插值公式可知,存在Fq上的對合多項式g(x),使得

Ag={al1,al2,…,alm,b1,f(b1),b2,f(b2),…,bi,f(bi)},

B

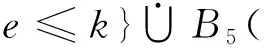
且

|Af∩Ag|=m, 0≤m≤n,

|Bf∩Bg|=j.

于是,對任意x∈Af,有g(x)∈Af,并且對(x:f(x))∈Bf,以下條件之一成立:

1)x,f(x)∈Ag;

2) (x:f(x))∈Bg;

3) 存在(x1:x2)∈Bf,使得(x1:x2)≠(x:f(x)),滿足(x:x1),(f(x):x2)∈Bg.

從而,由引理1.2可知f°g(x)為對合多項式.所以,若f(x)∈Fq[x]為Fq上的對合多項式,|Af|=n,n∈N,則

其中

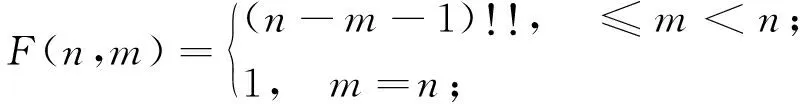
3 應用舉例

本節通過實例進一步驗證定理1.3.例3.1是對應于定理1.3中2)的例子,例3.2是對應于定理1.3中3)的例子.首先通過枚舉法得出F7上的所有對合多項式的真值表,然后通過MATLAB利用拉格朗日插值公式得出每個真值表對應的多項式形式,其結果如附錄表1～8所示.

例 3.1取f(x)=x5-x4+x3-x2+2x-1∈F7[x],則f(x)的真值表如下.

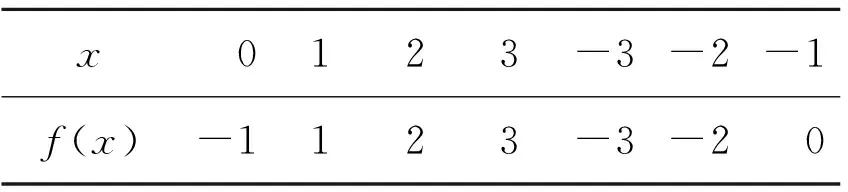
x0123-3-2-1f(x)-1123-3-20

由真值表可知:f(x)為F7上的對合多項式,且

Af={1,2,3,-3,-2},

Bf={(0:-1)}.

一方面,若g(x)為F7上的對合多項式,由定理1.3的2)可知

通過枚舉法將所有結果羅列出來后,再利用拉格朗日插值公式得到這些g(x),如附錄表9所示,共25個.

另一方面,F7上的所有對合多項式如附錄表1～8所示.經一一驗證可知,僅有表9中的對合多項式與f(x)復合后仍為對合多項式.

例 3.2取f(x)=x5∈F7[x],則f(x)的真值表如下.

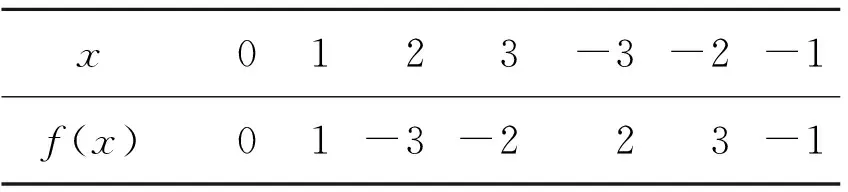
x0123-3-2-1f(x)01-3-223-1

由真值表可知:f(x)為F7上的對合多項式,且

Af={0,1,-1},

Bf={(2:-3),(3:-2)}.

一方面,若g(x)為F7上的對合多項式,則由定理1.3中的3)可知

通過枚舉法將所有結果羅列出來后,再利用拉格朗日插值公式得到這些g(x),如附錄表10所示,共24個.

另一方面,F7上的所有對合多項式如附錄表1～8所示.經一一驗證可知,僅有表10中的對合多項式與f(x)復合后仍為對合多項式.