臨床研究中交互作用、效應修飾的識別和評價

王瑞平 李斌

（上海市皮膚病醫院臨床研究與創新轉化中心 上海 200443）

臨床醫學研究尤其是在病例對照研究和隊列研究設計中，研究者在評估“暴露與結局”的關聯強度時，往往須要控制其他因素的影響，進而得到“暴露與結局”的真實關聯強度。影響臨床研究“暴露與結局”評估的因素主要有兩大類，一類是包括混雜偏倚在內的各種系統誤差所導致的偏倚，研究者應對此進行識別和控制；而另一類是交互作用和效應修飾，是兩個或多個因素相互依賴發生作用而產生的一種效應，對暴露因素作用于結局變量的效應起到“增強”“協同”“拮抗”等作用，研究者應對此進行識別和評估。本文將介紹交互作用和效應修飾的概念，交互作用的識別方法，以及評估交互作用和效應修飾的策略等內容，以期為研究者今后開展交互作用和效應修飾評價提供參考。

1 交互作用/效應修飾的概念

臨床研究中，交互作用一般指兩個或多個因素相互依賴發生作用而產生的一種效應。在生物學上是指兩個或多個因素相互依賴發生作用而引起疾病或預防控制疾病；而在統計學上，交互作用說明兩個因素在數量上的關聯。交互作用的識別和分析有利于描述疾病的特征，探索疾病的病因，在公共衛生領域和臨床上均具有重要意義。如果人群中的交互作用是由兩個因素引起，稱為效應修飾，主要變現為協同作用和拮抗作用。協同作用（synergism）是指兩個因素的聯合作用大于他們單獨作用之和；而拮抗作用（antagonism）是指兩個因素的聯合作用小于他們單獨作用之和。通常，可以通過分層分析對交互作用和效應修飾進行識別。

2 交互作用/效應修飾的識別

如本刊2022年第43卷第15期“臨床研究中混雜偏倚的識別和控制策略”[1]一文中所述，在臨床研究中，研究者須要識別并控制潛在的混雜偏倚；而對于交互作用，研究者則須要識別并對其進行描述和評價，而不是進行控制。同樣，分層分析是識別交互作用的常用方法。為方便研究者理解，本文仍引用“一項口服避孕藥（oral contraceptive, OC）和心肌梗死（myocardial infarction,MI）病例對照研究”[2]并對數據進行適當調整，以舉例說明。

在該項研究中，考慮到年齡與OC有關，也與MI有關，即考慮年齡是潛在的混雜因素。因此，將年齡按照＜40歲和≥40歲分為兩層，由此來判定年齡是否為OC與MI關聯的潛在混雜因素。如圖1所示，首先，根據提供的原始數據計算出OC與MI之間的關聯強度，即比值比（odd ratio, OR）＝2.20，95%置信區間（confidence interval, CI）：1.26～3.84。隨后，根據混雜因素判定的3個條件：①先判定年齡是否與OC有關，摘取兩層對照組患者數據（圖1中實線框數據），計算出年齡與OC之間的關聯強度OR為3.91；②其次再判定年齡與MI是否有關，摘取兩層未服用OC患者數據（圖1中虛線框內數據），計算出年齡與MI之間的關聯強度OR值為0.24；③最后，結合年齡不是OC與MI發病的中間環節。由此可以得出，年齡是潛在的混雜因素。

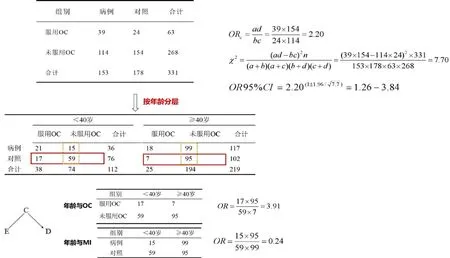
圖1 應用分層分析識別交互作用

進一步分別計算兩層中OC與MI之間的關聯強度。在＜40歲年齡層，OC與MI之間的關聯強度OR＝（ad）/（bc）＝（21×59）/（17×15）＝4.86；在≥40歲年齡層，OC與MI之間的關聯強度OR＝（ad）/（bc）＝（18×95）/（99×7）＝2.47，兩層之間的關聯強度（4.86＞2.47）相差明顯，說明年齡在OC與MI發病之間不均衡可比，年齡與OC之間可能產生了交互作用，共同導致MI的發生。

3 交互作用的評價

臨床研究中，發現不同因素之間的交互作用后應進行描述和評價。而評價一項研究中是否存在交互作用，以及交互作用的大小均依賴于模型，這主要包括了相加模型和相乘模型。為方便理解，本文將以圖示的方式進行說明。

如圖2所示，假設A和B是某人群中與疾病D有關聯的2個危險因素。A0B0表示A和B兩個因素均不存在；A1B0表示A因素存在B因素不存在；A0B1表示B因素存在A因素不存在；A1B1表示A因素和B因素均存在。同理，R00表示某人群既不暴露于A因素也不暴露于B因素的發病概率；R10表示某人群暴露于A因素而不暴露于B因素的發病概率；R01表示某人群暴露于B因素而不暴露于A因素的發病概率；R11表示某人群同時暴露于A和B兩個因素的發病概率。

圖2 應用分層分析識別交互作用

相加模型是評價基于同時起作用的A、B兩個因素的超額風險等于A因素的超額風險加上B因素的超額風 險。 當（R11－ R00） ＝（R10－ R00）+（R01－ R00）時，說明基于相加模型A、B兩個因素無交互作用；當（R11－R00）≠（R10－R00）＋（R01－ R00），說明基于相加模型的交互作用存在。在“一項吸煙與肺癌的隊列研究”中，研究對象同時暴露于吸煙和石棉后的肺癌發病率明顯高于僅暴露于吸煙的研究對象，以及僅暴露于石棉的研究對象。研究結果如圖3所示，現應用相加模型評估吸煙和石棉在肺癌發生過程中的交互作用。根據相加模型理論，首先計算同時暴露于石棉和吸煙的肺癌發病風險（R11－R00）＝1 500－60=1 440；隨后，分別計算僅暴露于石棉的肺癌發病風險（R01－R00）=300－60=240，僅暴露于吸煙的肺癌發病風險（R10－R00）＝300－60＝240；由此可得（R11－R00）＞[（R10－R00）＋（R01－R00）]。因此，基于相加模型，吸煙和石棉對肺癌的發生有交互作用，根據大小可判定為協同作用。須說明的是，在進行交互作用評價時，除發病率外，相對危險度（relative risk, RR）和OR同樣也適用。兩者判定公式分別為（RR11＋ RR00）＝（RR10＋ RR01）和（OR11＋ OR00）＝（OR10＋ OR01）。

圖3 基于相加模型描述和評價交互作用/效應修飾

與相加模型相似，相乘模型是評價同時起作用的A、B兩個因素的相對風險等于A因素的相對風險乘以B因素的相對風險。即當（R11/R00）＝（R10/R00）×（R01/R00）時，說明A、B兩個因素基于相乘模型無交互作用；當（R11/R00）≠（R10/R00）×（R01/R00），說明基于相乘模型的交互作用存在。仍以“一項吸煙與肺癌的隊列研究”為例，研究結果如圖4所示，現應用相乘模型評估吸煙和石棉在肺癌發生過程中的交互作用。根據相乘模型理論，首先計算同時暴露于石棉和吸煙的肺癌發病相對風險（R11/R00）＝1 500/60=25；隨后，分別計算僅暴露于石棉的肺癌發病相對風險（R01/R00）＝300/60＝5，僅暴露于吸煙的肺癌發病風險R10/R00＝300/60＝5；由此可得（R11/R00）＝（R10/R00）×（R01/R00）。因此，基于相乘模型，吸煙和石棉對肺癌的發生無交互作用。同樣地，在進行交互作用評價時，除發病率外，還可以運用RR或OR進行判定。兩者判定公式分別為（RR11×RR00）＝（RR10×RR01）和（OR11×OR00）＝（OR10×OR01）。

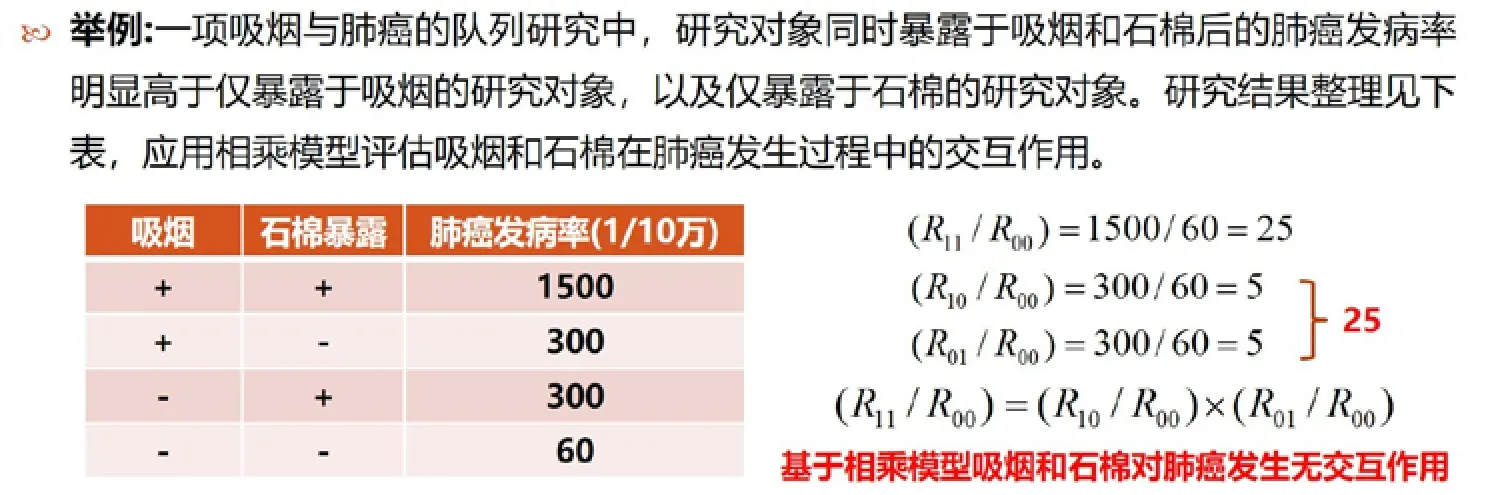
圖4 基于相乘模型描述和評價交互作用/效應修飾

綜上所述，相加模型是評價同時起作用的A、B兩個因素的超額風險等于A因素的超額風險加上B因素的超額風險，而相乘模型是評價同時起作用的A、B兩個因素的相對風險等于A因素的相對風險乘以B因素的相對風險。須注意的是，在臨床研究中，相加模型適用面更廣，而相乘模型多數用于基因相關的研究。另外，研究交互作用可以幫助人們了解這些因素的生物學特征，但是混雜因素并不是一個因素的固定不變的特征，其在一項研究中可能起到混雜的作用，卻也可能在另一項研究中，起到的是交互作用。因此，臨床研究中可能會出現以下4種情況：①有混雜，但無交互作用；②無混雜，僅為交互作用；③混雜和交互作用同時存在；④混雜和交互作用均不存在。研究者在評價時應根據具體情況進行分析。

至于在前文所提到的“一項OC與MI病例對照研究”中，運用分層分析初步識別年齡和OC對MI存在潛在的交互作用后，接下來即可開展交互作用的描述和評價。如圖5所示，首先根據分層后的數據進行叉生分析，計算OR11、OR10、OR01、OR00；然后分別用相加模型和相乘模型進行評價：基于相加模型，得到（R11－R00）≠（R10－R00）＋（R01－R00），即年齡和OC對MI基于相加模型存在交互作用；基于相乘模型，同樣得到（R11/R00）≠（R10/R00）×（R01/R00），即年齡和OC對MI基于相乘模型也存在交互作用。

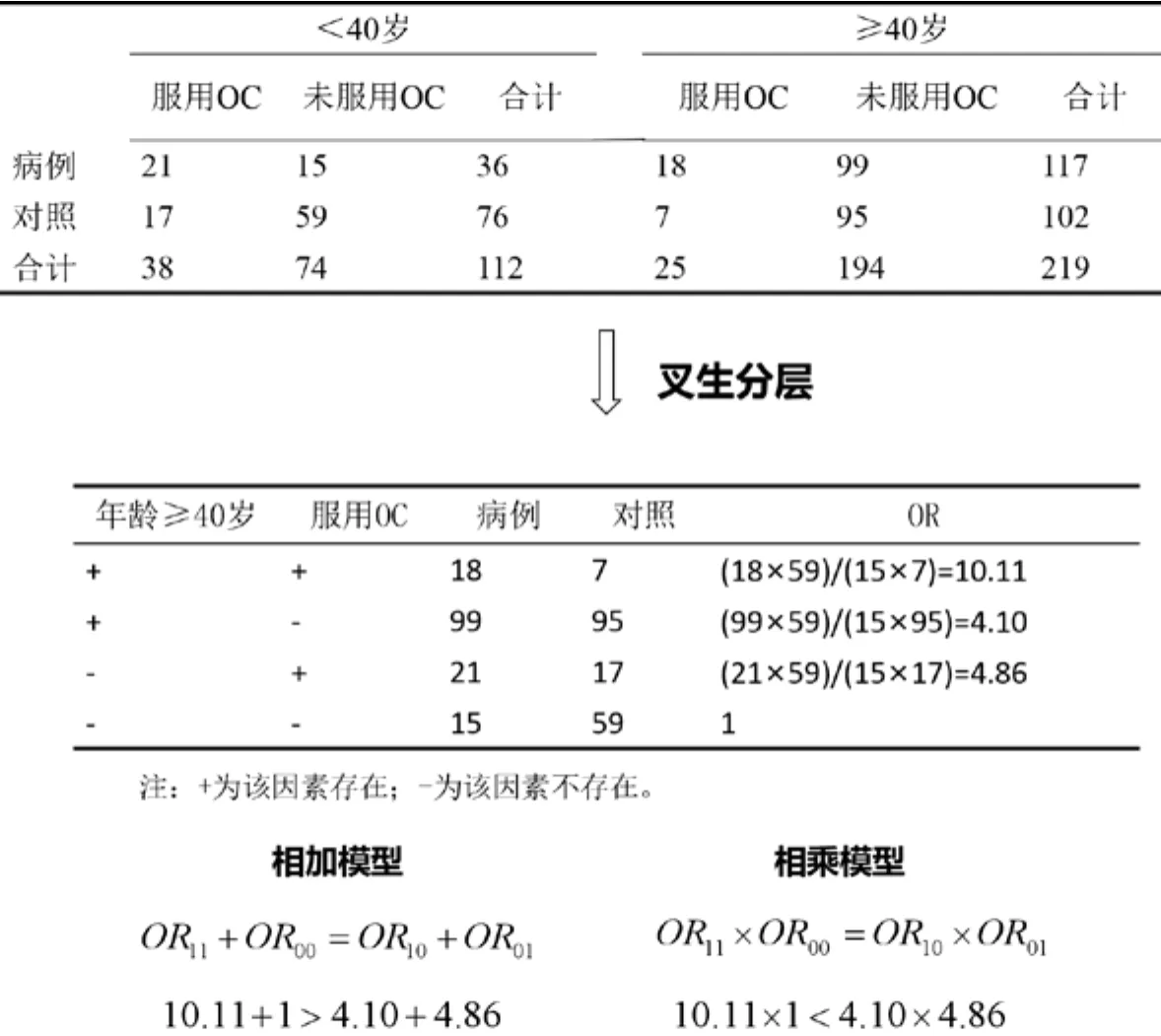
圖5 年齡和OC對MI影響的交互作用評價