求多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

◎馬 悅 傅 勤

(江蘇省蘇州市蘇州科技大學(xué)數(shù)學(xué)科學(xué)學(xué)院，江蘇 蘇州 215009)

一、引 言

多元函數(shù)微分學(xué)是高等數(shù)學(xué)和數(shù)學(xué)分析課程中的重要內(nèi)容，其中的復(fù)合函數(shù)微分法主要討論了復(fù)合函數(shù)的可微性、偏導(dǎo)數(shù)與全微分在研究復(fù)合函數(shù)的一般求導(dǎo)法則時(shí)，教材中運(yùn)用了鏈?zhǔn)椒▌t的求導(dǎo)方法但是在計(jì)算較復(fù)雜的復(fù)合函數(shù)時(shí)，簡(jiǎn)單地運(yùn)用鏈?zhǔn)椒▌t會(huì)使問題的解決變得煩瑣文后的參考文獻(xiàn)給出了多元函數(shù)求偏導(dǎo)數(shù)的一般公式，并沒有給出求多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式為了解決此類問題，本文將從推導(dǎo)求二重復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式出發(fā)，研究求三重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式，并進(jìn)一步研究求多重任意元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

二、求二重、三重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

(一)文后參考文獻(xiàn)中的已有公式

若(,…,)在點(diǎn)(,…,)可微，而=(,…,),=1,2,…,在點(diǎn)(,…,) 具有關(guān)于(=1,2,…,)的偏導(dǎo)數(shù)，則復(fù)合函數(shù)

((,…,),(,…,),…,(,…,))

關(guān)于自變量的偏導(dǎo)數(shù)是

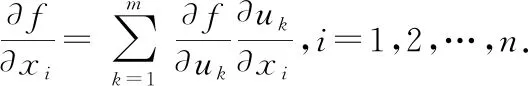
我們注意到：上述方法中每個(gè)函數(shù)的變量個(gè)數(shù)是相同的那么能否將此公式推廣到更為一般的形式，即考慮到每個(gè)函數(shù)的變量個(gè)數(shù)不相同的情況呢？

文后的參考文獻(xiàn)[3]～[7]提出了運(yùn)用叉樹表示元函數(shù)偏導(dǎo)數(shù)關(guān)系的樹型法則，使得相應(yīng)的計(jì)算過程可簡(jiǎn)化為：遍歷各枝(子)，最后到葉；兄弟用加，下輩用乘這個(gè)方法對(duì)之后研究多重多元復(fù)合函數(shù)的偏導(dǎo)數(shù)有很大的啟發(fā)相應(yīng)地運(yùn)用三元樹型法則計(jì)算三重復(fù)合函數(shù)偏導(dǎo)數(shù)的過程如下所示

函數(shù)是關(guān)于函數(shù),,的復(fù)合函數(shù)，函數(shù),,是分別關(guān)于自變量,,的函數(shù)，寫出表達(dá)式如下：

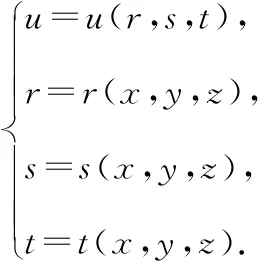
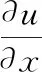
當(dāng)天夜里秦川將她占有，或者說當(dāng)天夜里她將秦川占有，她認(rèn)為后者或許更恰當(dāng)一些。她不是隨便的女人，她無比保守，可是見到秦川，她就想將自己交付出去。她不是淫蕩的女人，她無比清純，可是見到赤裸的秦川，她甚至想跪下去親吻秦川的腳趾。那幾天里，她認(rèn)為自己是世界上最合格的充氣娃娃。

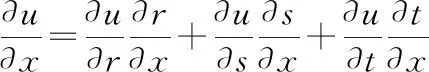
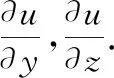
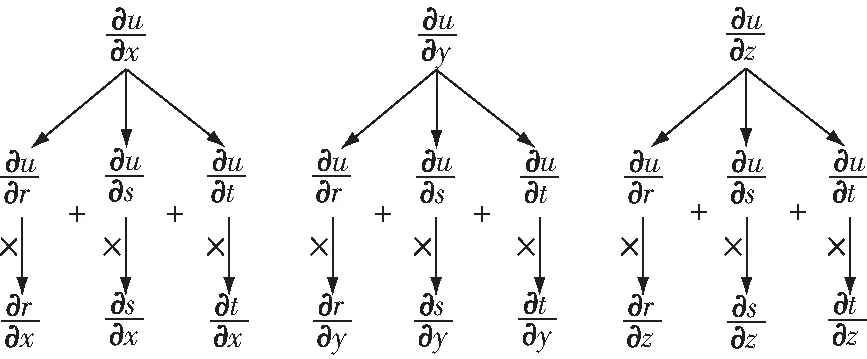
我們注意到：這些文獻(xiàn)對(duì)樹型法則的相關(guān)研究為多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的計(jì)算提供了很好的方法，但并沒有給出求多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式本文將針對(duì)求多重任意元函數(shù)偏導(dǎo)數(shù)的一般公式進(jìn)行更深入的研究

(二)求二重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

1若=(,…,)在點(diǎn)(,…,)可微，=(,…,),=1,2,…,,=1,2,…,在點(diǎn)(,…,)具有關(guān)于(=1,2,…,)的偏導(dǎo)數(shù)，則復(fù)合函數(shù)

((,…,),(,…,),…,(,…,))

關(guān)于自變量的偏導(dǎo)數(shù)是

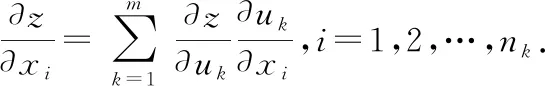
由定理?xiàng)l件可知

①

其中,,…,,,,…,,,,…,為當(dāng)Δ,Δ,…,Δ趨于零時(shí)的無窮小又由=(,…,)在點(diǎn)(,…,)可微，所以

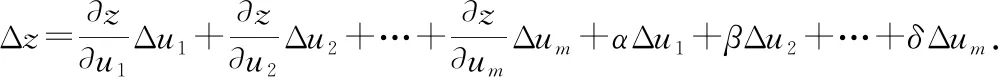
②

其中,,…,為當(dāng)Δ,Δ,…,Δ趨于零時(shí)的無窮小將①代入②，可得

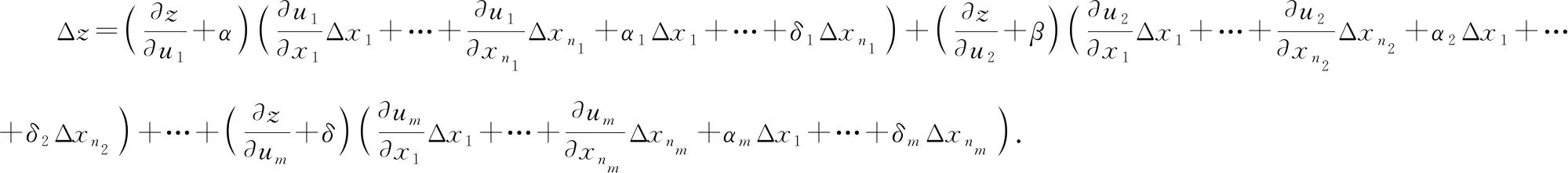
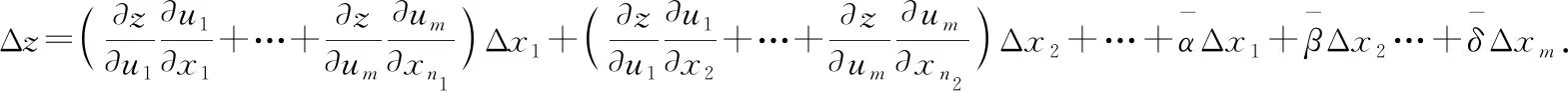
其中,

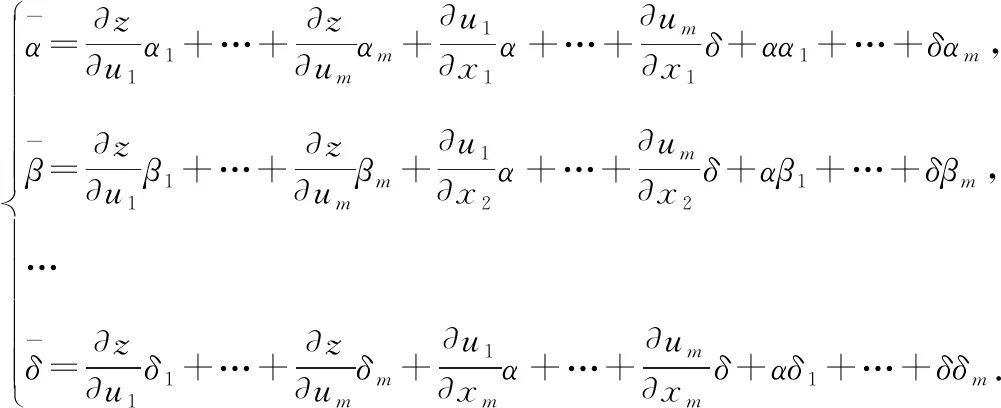
由此可以得到關(guān)于自變量的偏導(dǎo)數(shù):

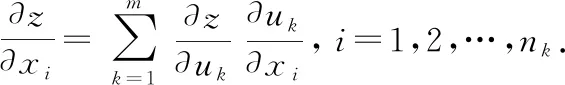
(三)求三重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

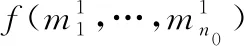
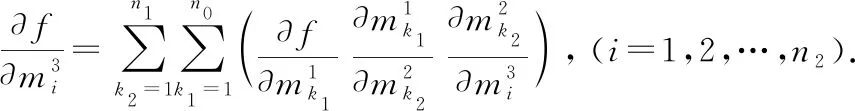
由定理?xiàng)l件可知

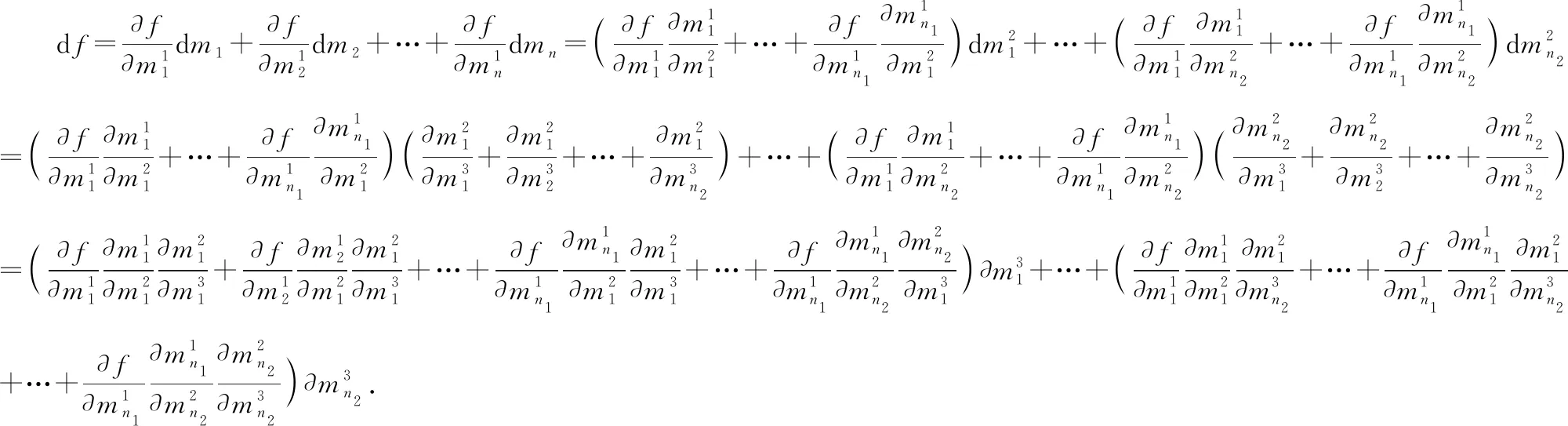
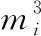
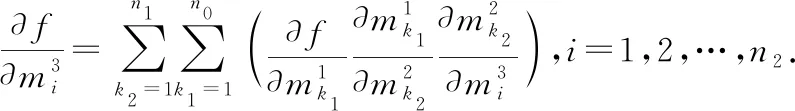
三、求多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式

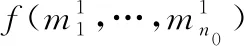
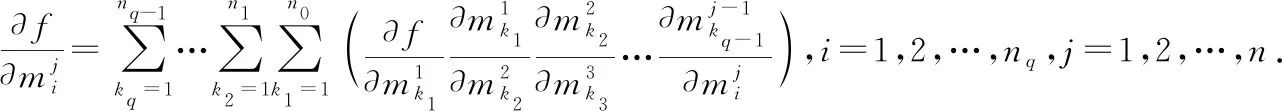
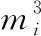
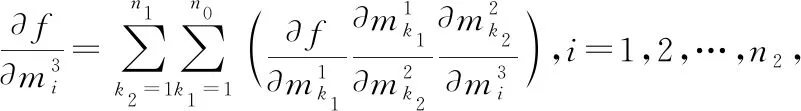
即結(jié)論成立

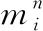
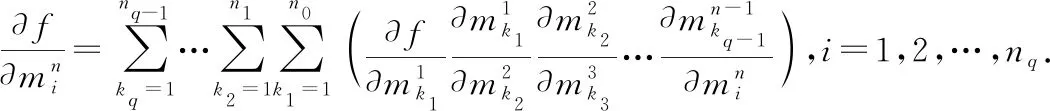
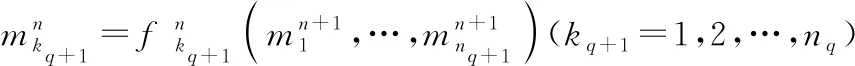
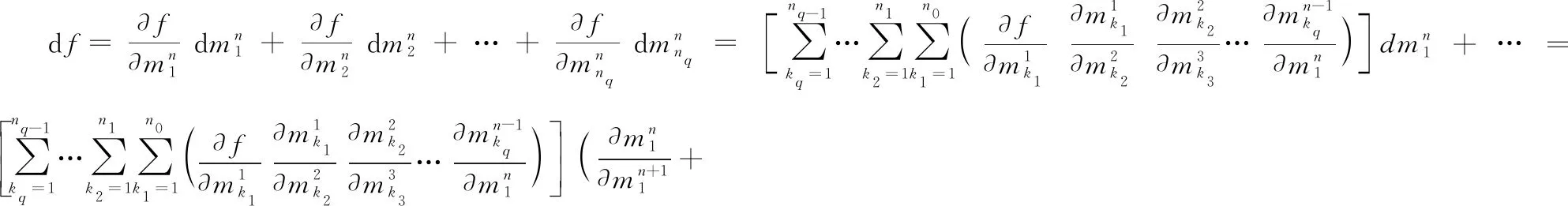
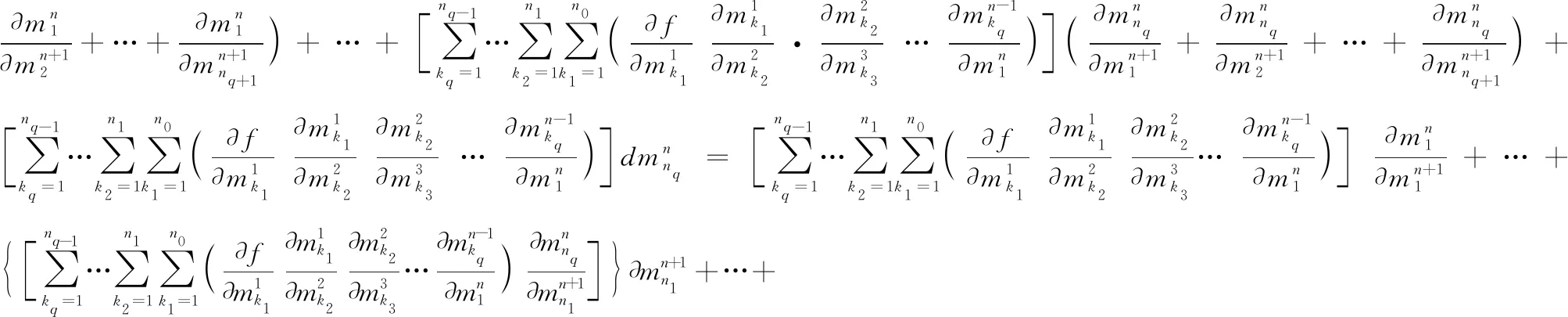
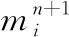
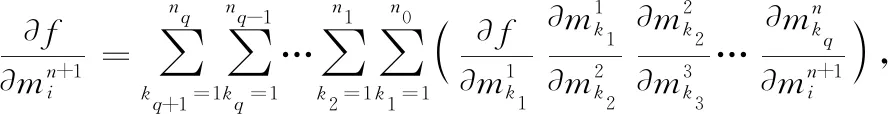
=1,2,…,+1

因此，對(duì)于+1重(為任意自然數(shù))元復(fù)合函數(shù)，結(jié)論也成立證畢

四、結(jié) 語

本文從教材上已有的二重復(fù)合函數(shù)求偏導(dǎo)數(shù)的計(jì)算方法入手，嘗試運(yùn)用樹型法則對(duì)多元多重函數(shù)進(jìn)行偏導(dǎo)數(shù)的求解，通過研究得出求三重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式，然后利用數(shù)學(xué)歸納法進(jìn)一步推導(dǎo)出了求多重多元復(fù)合函數(shù)偏導(dǎo)數(shù)的一般公式