基于組合預(yù)測(cè)模型下某區(qū)碳排放的預(yù)測(cè)研究

陳莎莎

（廣東一方環(huán)保科技有限公司，廣東 廣州 510000）

0 引言

為完成對(duì)區(qū)域內(nèi)碳排放的有效預(yù)測(cè)，國(guó)內(nèi)外相關(guān)研究人員提出了較多的預(yù)測(cè)模型。在碳排放影響因素解析方面，現(xiàn)階段常用的模型算法主要有LDMI（對(duì)數(shù)平均迪式分解法）、Kaya（卡亞不等式）等，為碳排放量的預(yù)測(cè)奠定了基礎(chǔ)。在碳排放預(yù)測(cè)方面，相關(guān)研究人員提出了CSO（雞群算法）、FLN（快速學(xué)習(xí)網(wǎng)）等很多模型算法，但單一的模型存在預(yù)測(cè)精度方面的缺陷，為解決該問(wèn)題，該文對(duì)CSO與FLN兩種算法模型進(jìn)行組合應(yīng)用，旨在解決區(qū)域內(nèi)碳排放的精準(zhǔn)預(yù)測(cè)難題。

1 碳排放計(jì)算方法與影響因素

1.1 碳排放計(jì)算方法

碳排放的計(jì)算涉及的碳源包括能源消費(fèi)、秸稈燃燒、工業(yè)生產(chǎn)、廢水排放、糞便發(fā)酵以及甲烷排放等內(nèi)容，需要核算的碳匯包括城市綠地、耕地林與果園等區(qū)域，碳排放結(jié)果即為碳源與碳匯的差值，相關(guān)技術(shù)參數(shù)見(jiàn)表1、表2。

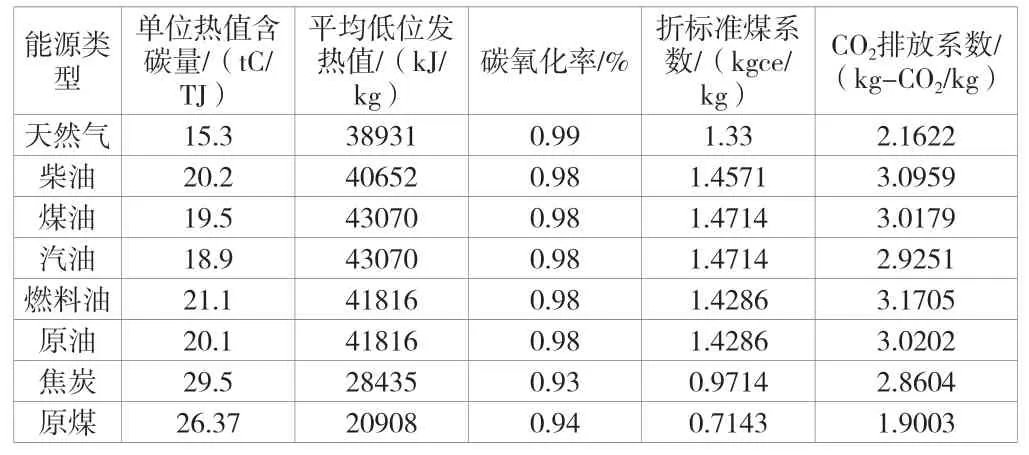
表1 各類(lèi)能源碳排放的相關(guān)系數(shù)

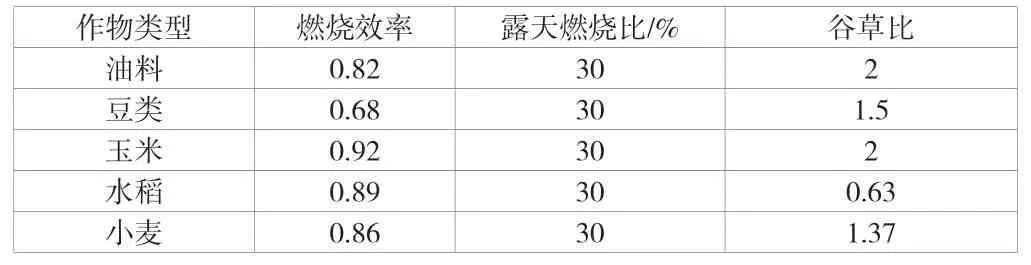
表2 秸稈燃燒碳排放計(jì)算主要參數(shù)

1.2 碳排放影響因素

為研究影響區(qū)域內(nèi)碳排放的影響因素，該文通過(guò)STIRPAT模型進(jìn)行評(píng)估分析。該模型能夠?qū)Νh(huán)境壓力、技術(shù)、富裕度以及人口之間的聯(lián)系進(jìn)行分析，如公式（1）所示。

式中：為常數(shù)；為誤差；為估算指數(shù)。通過(guò)兩邊取對(duì)數(shù)得到公式（2）。

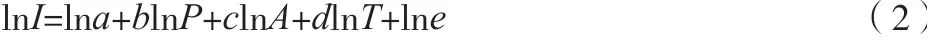
基于STIPRAT模型對(duì)上述公式進(jìn)行擴(kuò)展，將產(chǎn)業(yè)結(jié)構(gòu)、能源結(jié)構(gòu)、對(duì)外開(kāi)發(fā)納入模型，如公式（3）所示。

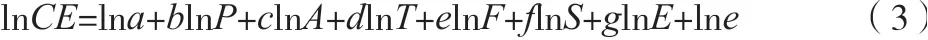
式中：即為碳排放量；為能源結(jié)構(gòu)；為產(chǎn)業(yè)結(jié)構(gòu)；為對(duì)外開(kāi)放；人口為年末常住人口；技術(shù)取決于能源強(qiáng)度；富裕度為人均GDP。……