對高中數學新教材一道三角恒等變換習題的拓廣探索

張靜元

(云南省昆明市教育科學研究院 650000)

1 問題呈現

題目(人民教育出版社《普通高中教科書數學必修第一冊A版》第230頁，簡單的三角恒等變換習題5.5拓廣探索第18題)觀察以下各等式

分析上述各式的共同特點，寫出能反映一般規(guī)律的等式，并對等式的正確性作出證明.

2 問題解決方法

2.1 從角的特征探索發(fā)現共同規(guī)律

綜合考查三個等式中的角發(fā)現共同規(guī)律：

60°=30°+30°；45°=30°+15°；50°=30°+20°.

以第三個等式為例證明：

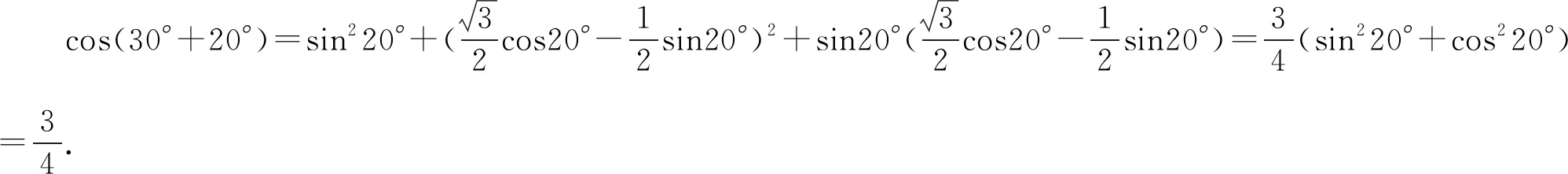
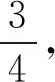
2.2 寫出反映一般規(guī)律的等式

三個等式中給出的兩個角60°，30°；45°，15°；50°，20°都滿足β=30°+α，則一般規(guī)律的等式為：

2.3 從不同的角度證明等式的正確性

思路1 和差角公式.

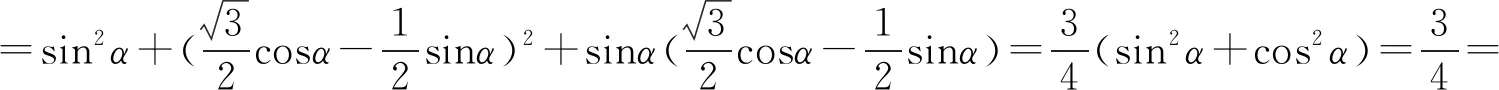
思路2 降冪擴角公式.

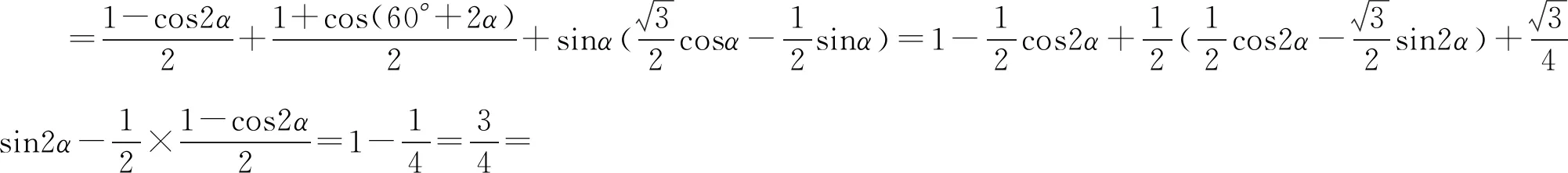
思路3 三角函數在單位圓上的定義.

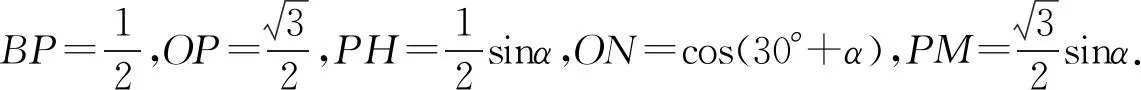
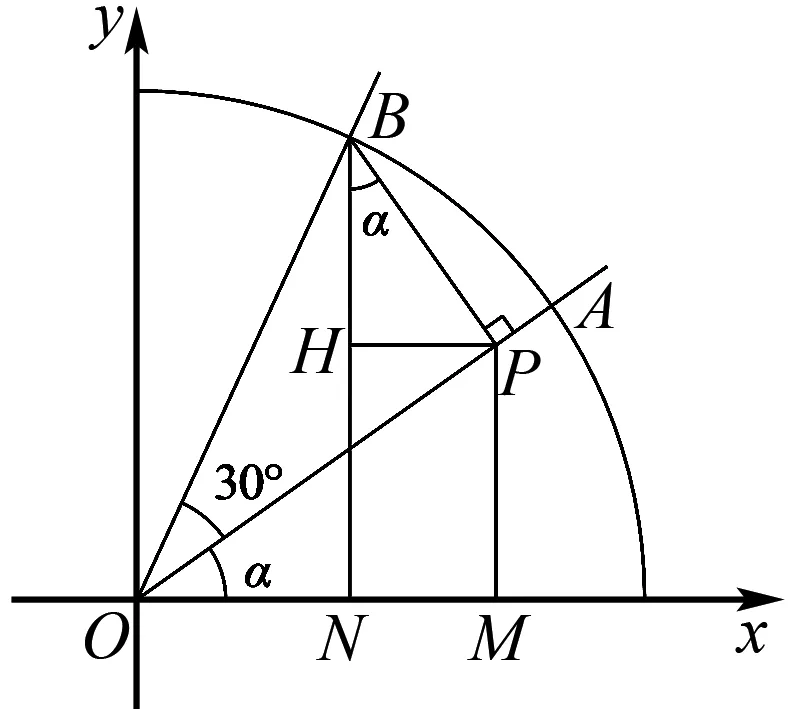
圖1

思路4解直角三角形.

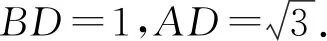
圖2 圖3

當α為鈍角時，如圖3，同理可證.同理，當α為特殊角或大于180°，等式成立.

思路5解三角形.

在△ABC中，A=α，B=30°，則C=150°-α.設b=1，由正弦定理,得a=2sinα，c=2sin(150°-α).

由余弦定理，得c2=a2+b2-2abcosC，則4sin2(150°-α)=4sin2α+1-4sinαcos(150°-α).

3 問題探索

3.1 統(tǒng)一函數名

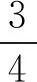
思考1 對于等式中的60°，能改為任意角嗎？

猜想：對任意的角β，sin2α+sin2(β-α)+sinαsin(β-α)=sin2β.下面取特值驗證：

當β=90°，等式左邊=sin2α+cos2α+sinαcosα=1+sinαcosα，等式右邊=1，顯然對任意角α等式不正確.所以，對于任意的角β，sin2α+sin2(β-α)+sinαsin(β-α)≠sin2β.

既然對任意角β等式不成立，那么角β能取到哪些值才能使等式成立？

思考2 探索角β取何值能使猜想正確.

把β作為自變量，構造函數f(x)=sin2α+sin2(x-α)+sinαsin(x-α)-sin2x，其中α為參數，用計算機作出函數f(x)的圖象，考查函數f(x)的零點，即為等式成立的情況：

如圖4,函數f(x)部分零點從左至右依次為：

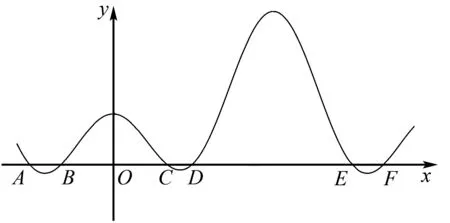
圖4

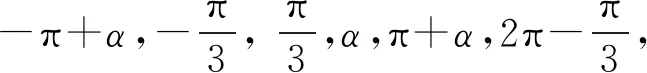
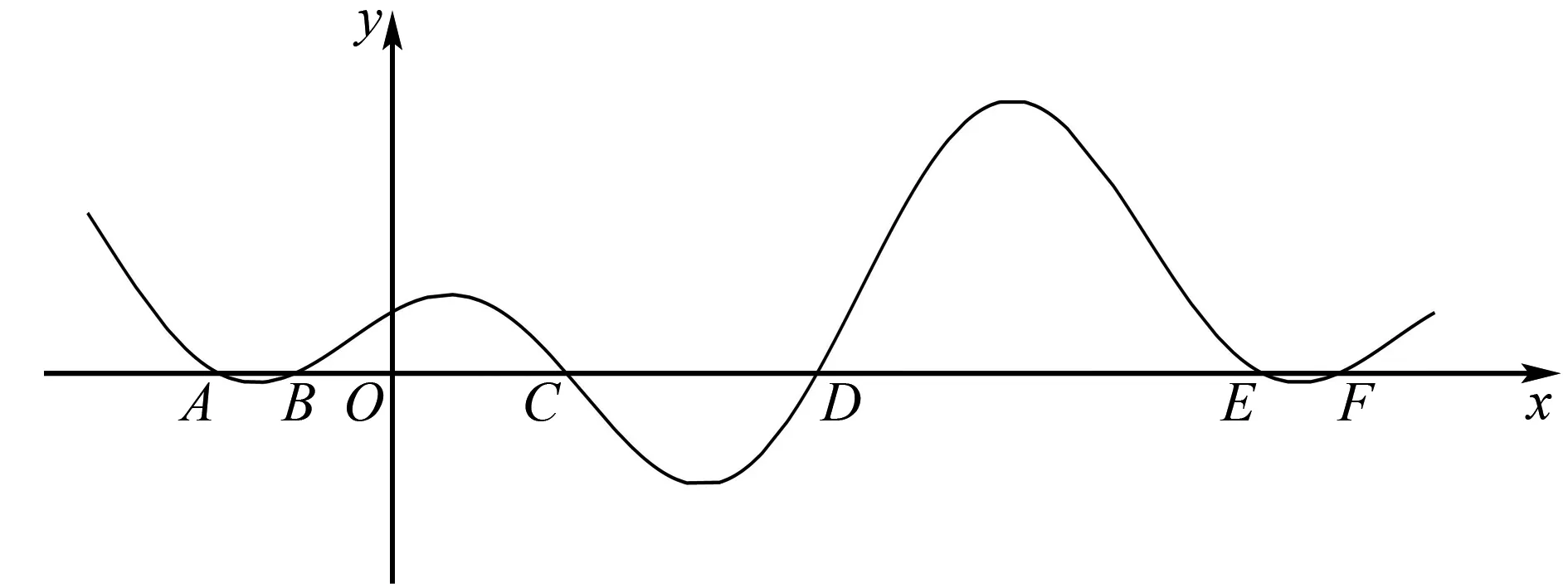
圖5

3.2 探索角的特征

由于sin260°=sin2120°，等式寫成sin2α+sin2(60°-α)+sinαsin(60°-α)=sin2120°，發(fā)現α+(60°-α)+120°=180°，如果規(guī)定這三個角在(0°,180°)內，聯想這三個角為△ABC的內角，猜想sin2A+sin2B+sinAsinB=sin2C，其中A+B+C=180°.由于上面的探索，等式不能對任意的角C都成立，下面探索在△ABC中，滿足什么條件，等式sin2A+sin2B+sinAsinB=sin2C能成立.

3.3 拓廣問題

通過探索發(fā)現，在三角形中，由余弦定理a2+b2-2abcosC=c2變形公式可得：sin2A+sin2B-2sinAsinBcosC=sin2C.教科書中的三個等式，就是余弦定理變形公式中C=120°，A+B=60°的情形.歸納為：sin2A+sin2B-2sinAsinBcos120°=sin2120°，其中A+B=60°.

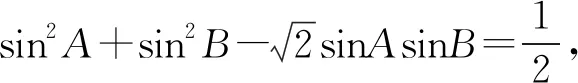
通過以上的探索，追溯等式成立的源頭，這一類等式是余弦定理在一定條件下的情況，通過統(tǒng)一函數名，發(fā)現三個角恰好為一個三角形的三個內角，借助正、余弦定理得到一般情況都能成立的條件.將問題拓廣，對鍛煉學生思維，培養(yǎng)探究意識，學會用不同路徑去探索數學問題，有較好的示范性.