對一道清華測試題的探究、變式及反思總結

劉海濤

(安徽省蕪湖市第一中學 241000)

《中國高考評價體系》指出：高考要求學生能夠觸類旁通、融會貫通，既包括同一層面、橫向的交互融合，也包括不同層面之間、縱向的融會貫通.高考要從“知識立意”轉向“能力立意”，考查學生的“關鍵能力”和“核心素養”.這就要求學生在學習中，學會靈活運用所學知識分析、解決問題，達到從“解題”向“解決問題”的轉變，對于一些典型問題，能夠從不同角度思考，尋求不同的解法，以一題多解的方式尋求知識間的內在聯系，構建知識的網絡體系，加深對問題的本質認識，從而拓寬解題視野，發散解題思維，提升學習興趣，提高解題能力.在清華大學2021年11月舉辦的中學生標準學術能力測試中，有一道二元分式函數最值問題，筆者結合學生的作答情況整理成文，現與讀者分享交流，以期拋磚引玉.

1 試題呈現與分析

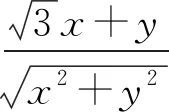
分析該題形式上以圓的方程(二元二次方程)為背景命題，主要考查分析、解決二元二次問題的能力，強化對轉化與化歸、函數與方程、消元與不等式求最值等數學思想方法的考查，體現了邏輯推理、數學運算、直觀抽象等數學核心素養.試題結構雖簡單、明了，但內涵豐富，值得研究，以發揮該題的最大價值.

2 解法探究

角度1分式齊次化，比值換元,化二次函數為一次函數.

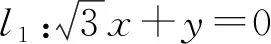
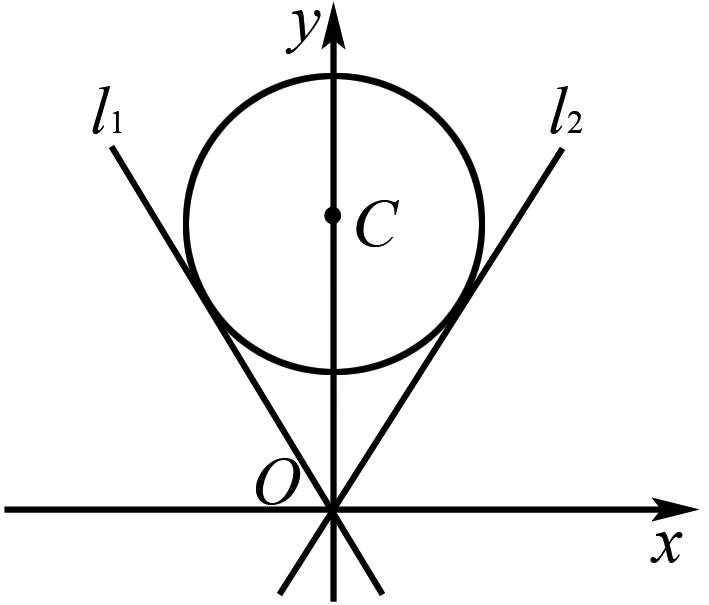
圖1

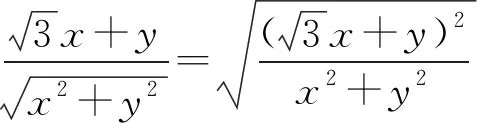
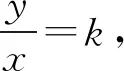
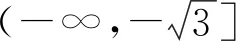
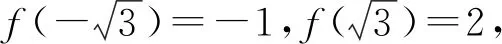
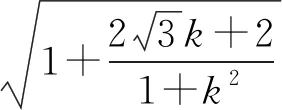
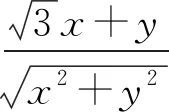
角度2聯想點到直線距離和兩點間距離公式，轉化為直角三角形內角的正弦值問題.

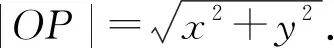
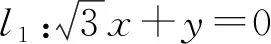
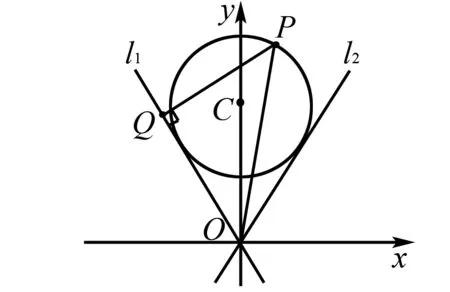
圖2

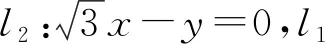
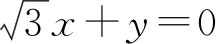
角度3聯想點到直線距離公式，轉化為距離問題.

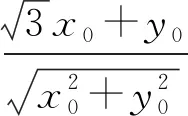
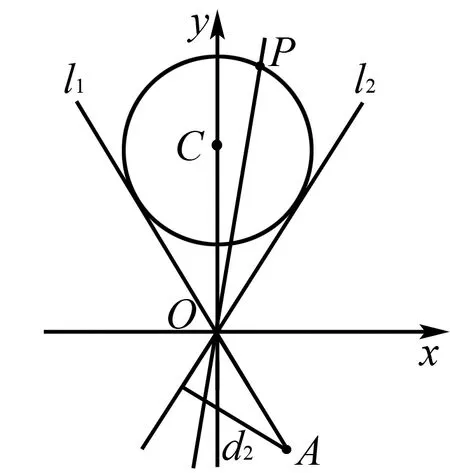
圖3

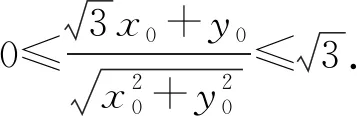
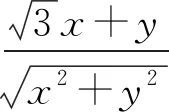
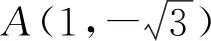
角度4聯想向量夾角余弦公式，轉化為余弦函數問題.

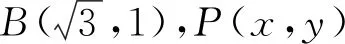
圖4

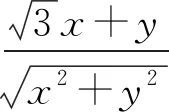
角度5聯想三角函數定義，轉化為三角函數問題.

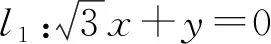
圖5

根據三角函數的定義，有

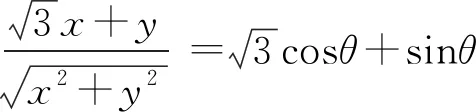
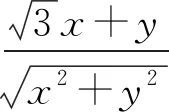
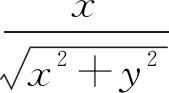
角度6極坐標換元，轉化為三角函數問題.

解法6如圖5，以坐標原點為極點，x軸非負半軸為極軸建立極坐標系，設P(ρ,θ)為圓C上一點，則θ∈[60°,120°].

評注極坐標換元法是解決二次函數問題的常用解法，文[3]對極坐標換元在二元函數問題中的應用做了詳細的介紹，讀者可以參考.

3 變式訓練

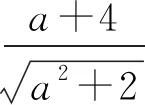
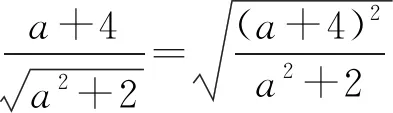
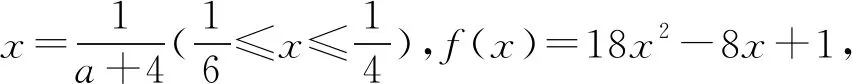
上述計算分析表明，高架橋、地鐵站同期同位分離式合建結構在靜力工況下安全可靠。為分析其抗震性能，采用MIDAS大型巖土隧道有限元軟件GTS建立三維有限元模型(見圖9)，進行抗震動力時程計算分析。

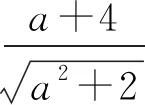
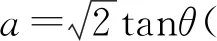
=3sin(θ+φ),

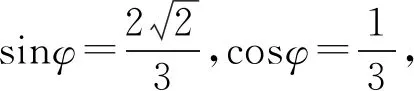
由φ≤θ+φ≤θ0+φ，

sin(θ0+φ)=sinθ0cosφ+cosθ0sinφ

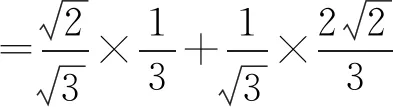
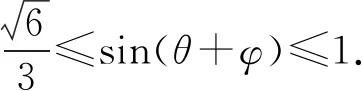
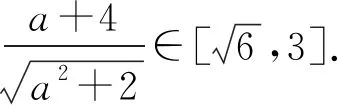
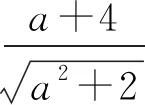
解法3(利用導數判斷單調性法)

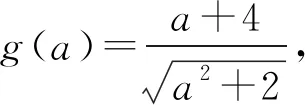
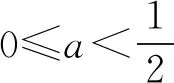
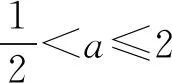
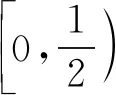
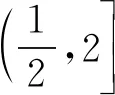
所以g(a)min=min{g(0),g(2)}

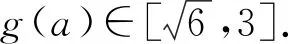
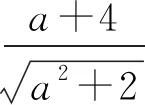
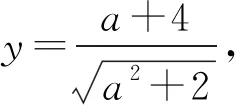
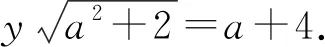
即(y2-1)a2-8a+2y2-16=0.

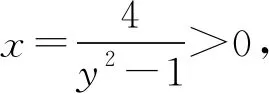
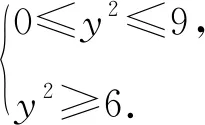
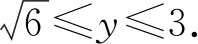
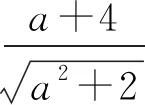
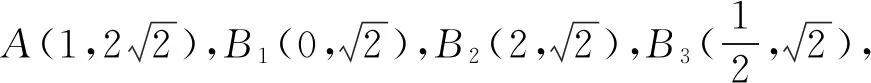
圖6

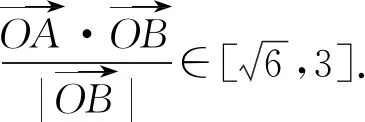
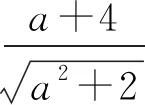
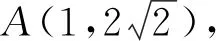
由于0≤a≤2，

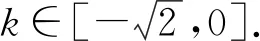
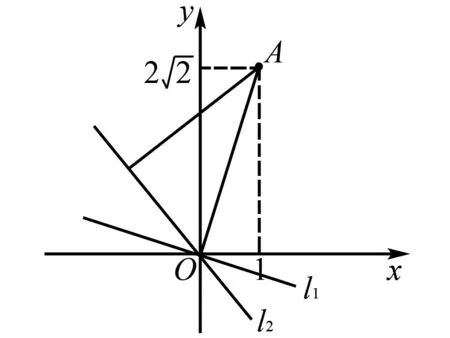
圖7

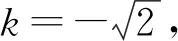
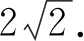
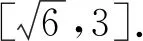
4 反思總結

4.1 一題多解，提高解題能力

數學離不開解題，數學研究的過程就是解決問題的過程，掌握數學的一個重要標志就是善于解題.可見，解題是一名教者的必備技能，技能的形成并非一朝一夕，而在于日積月累.數學解題是鞏固基礎知識、落實基本技能、感悟思想方法、提升思維敏銳度的系統活動，所以對一道典型問題進行多角度的分析與解答是非常必要的.筆者從六個角度對一道清華測試題予以分析，給出六種不同的解法，解法1是在觀察出分式的齊次化特征后，比值換元為一次函數，再以導數為工具求函數最值.解法2至5是基于函數式的結構特征，聯想所學的基本概念、公式，構造出函數式的幾何意義解題，其中解法2和3聯想點到直線的距離公式，分別將函數式轉化為直角三角形內角的正弦值問題和距離問題；解法4聯想向量夾角余弦公式，轉化為余弦函數問題；解法5聯想三角函數定義，轉化為三角函數問題.解法6通過極坐標換元法，同樣將問題轉化為三角函數問題，與解法5異曲同工.用多種方法解答同一道數學題，不僅能更牢固地掌握相關的數學知識，還能更靈活地運用所學知識，加強對數學整體性的理解與認識．通過一題多解，分析、比較各種解法，可以找到最佳的解題途徑，從而發散學生的思維能力，對鞏固數學知識和提高解題能力大有裨益．

4.2 夯實基本知識，強化通性通法

《普通高中數學課程標準(2017年版)》指出：在數學高考命題中，考查內容應圍繞數學內容主線，聚焦學生對重要數學概念、性質、方法的理解和應用，強調基礎性；注重數學本質和通性通法.因此，筆者認為在日常的解題教學中，教師應加強基礎知識、基本技能和基本數學思想方法的訓練，以提高學生解題的基本活動經驗.我們尋求一題多解，但不能滿足于一題多解，更不能為了一題多解而多解，而是要在解答的過程中總結出哪種方法適合哪類題型，選擇哪個方法更加合理、高效，對于一些常考題型，甚至于必考題型，教師要指導學生總結該類問題的“通性通法”，形成解題模型.通過文中對問題的多種解法不難看出，六種解法間的計算量和思維深度都有差別，但也都是解決類似分式函數的通法，那如何進行“通性通法”的訓練呢？筆者認為，所謂“通性通法”一定是建立在對問題形式、結構、特征等有著深刻理解的基礎之上，在有多種方法選擇的情況下，能快速找到最合理、高效的方法來完成解答.在日常的解題教學中，教師要指導學生分析每一種解法的優與劣，打破總是求導判斷單調性的類似經驗解題的慣性思維，如解法1就是最常規解法，雖思路順暢，但過程冗長、計算量大；解法2至5根據函數式結構特征，聯想點到直線距離公式、向量數量積、三角函數定義式、數形結合解出題目；解法6直接極坐標換元，轉化為三角函數問題，直接了當，干凈利落.因此，教師在解題教學中要指導學生如何根據問題特征，設計最合適的算理，選擇最佳的解法，這樣在平常的考試及最終的高考中才能“以不變應萬變”，順利完成考試.