運用相位差解決機械波中的疑難問題

周國慶

(江蘇省金壇區第一中學 213200)

人教版選擇性必修第一冊P37，“做簡諧運動的物體處于一個周期中的哪個狀態叫相位；兩個頻率相同的簡諧運動相位之差叫相位差.當φ1>φ2時，Δφ=φ1-φ2此時，我們說1的相位比2超前Δφ，或2的相位比1滯后Δφ”.筆者認為這種超前或滯后本質上體現的是質點振動過程中的“時空性”，即質點振動時間的先后或質點平衡位置距波源的前后(遠近).以下是筆者分別從時間和空間兩個維度對相位差(Δφ)和它們的關系進行的歸納.

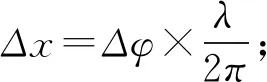
例1(2021·甲卷)均勻介質中質點A、B的平衡位置位于x軸上，坐標分別為0和xB=16cm.某簡諧橫波沿x軸正方向傳播，波速為v=20cm/s，波長大于20cm，振幅為y=1cm，且傳播時無衰減.t=0時刻A、B偏離平衡位置的位移大小相等、方向相同，運動方向相反，此后每隔Δt=0.6s兩者偏離平衡位置的位移大小相等、方向相同.已知在t1時刻(t1>0)，質點A位于波峰.求：

(1)從t1時刻開始，質點B最少要經過多長時間位于波峰；

(2)t1時刻質點B偏離平衡位置的位移.

解(1)t1時刻(t1>0)，質點A位于波峰，波形沿x軸正方向傳播，該波形傳播到B經歷的時間：

則質點B最少要經歷0.8s時間位于波峰；

(2)t=0時刻A、B偏離平衡位置的位移大小相等、方向相同，運動方向相反，此后每隔Δt=0.6s兩者偏離平衡位置的位移大小相等、方向相同.因為每經過半個周期質點運動到與該點對稱的位置，所以可得出：

波長：λ=vT=20×1.2cm=24cm

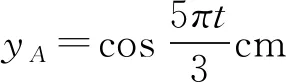
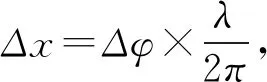
B滯后A振動，所以B的振動方程：

在t1時刻(t1>0)，質點A位于波峰,即yA=1cm, 不難求得此時yB= -0.5cm

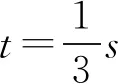
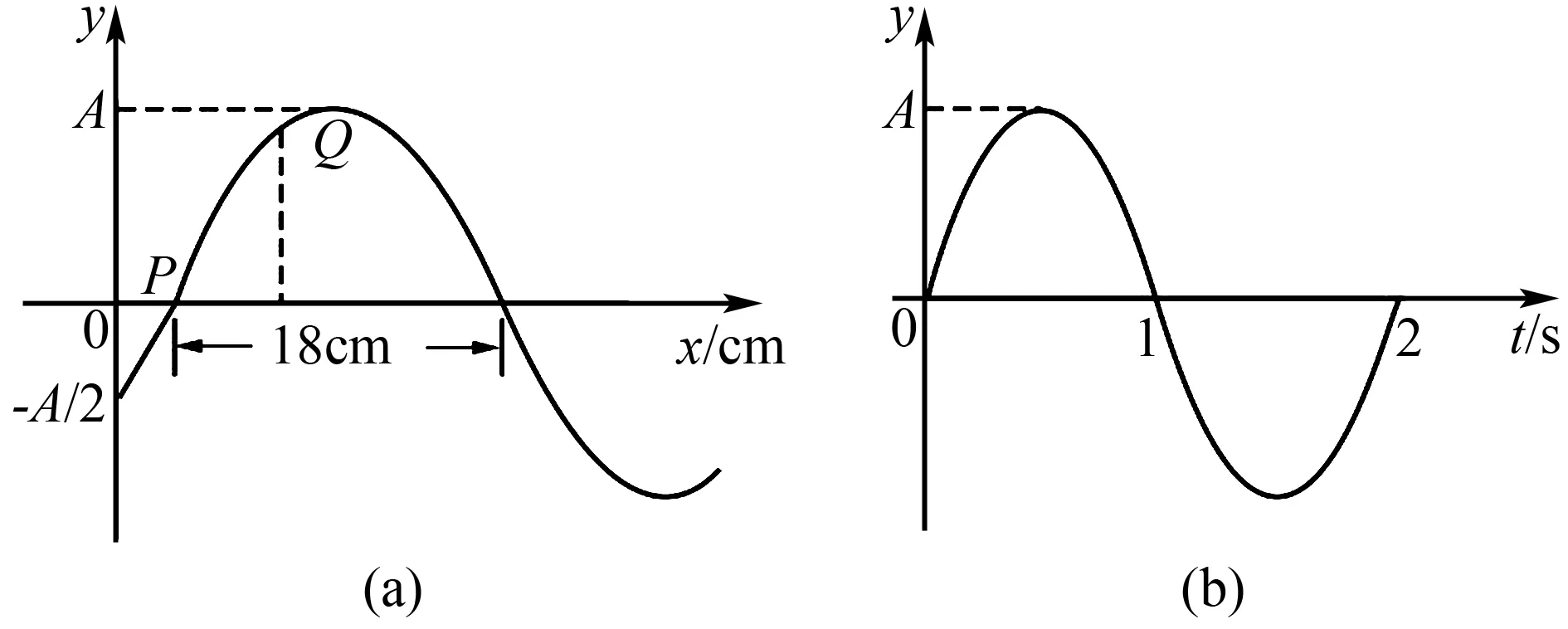
圖1

解略

例3甲、乙為一列沿x軸方向傳播的簡諧橫波上的兩個質點，兩質點平衡位置的間距為x=3m，圖2中的實線和虛線分別為質點乙和質點甲的振動圖像.如果波由質點甲向質點乙傳播，求該波的傳播速度.

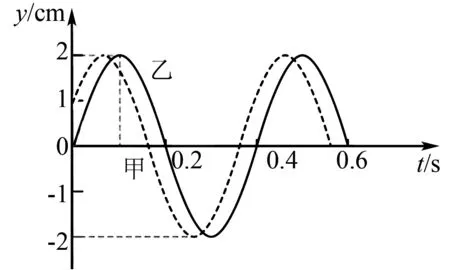
圖2

解由圖像可得，兩質點的振幅均為A=2 cm，周期為T=0.4 s

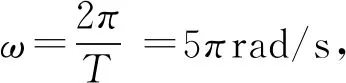
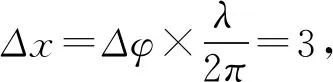
例4如圖3所示，圖3(a)為一列沿x軸傳播的簡諧橫波在某時刻的波形圖，P為平衡位置在x=17.5cm的質點，圖3(b)為此波中平衡位置坐標x=10cm的質點從該時刻起的振動圖象，求從該時刻起，P點第一次回到平衡位置通過的路程.

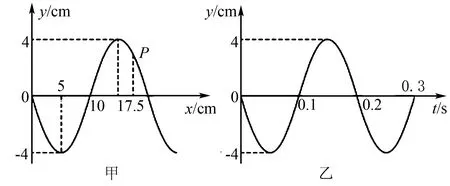
圖3

解由圖3(a)、圖3(b)兩圖知λ=20cm,T=0.2s得V=1m/s.由圖3(b)還可判斷x=10cm的質點該時刻振動方向向下，因此波以1m/s沿x軸正方向傳播.

設x=15cm處的質點為Q點，此時振動方程：

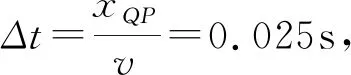
要注意的是，用相位差解決問題時，初相位的確定是關鍵，很多學生會忽視初相位與質點振動方向的關系而造成錯解，下面以2016年天津高考第7題為例.

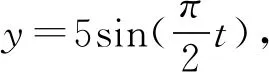
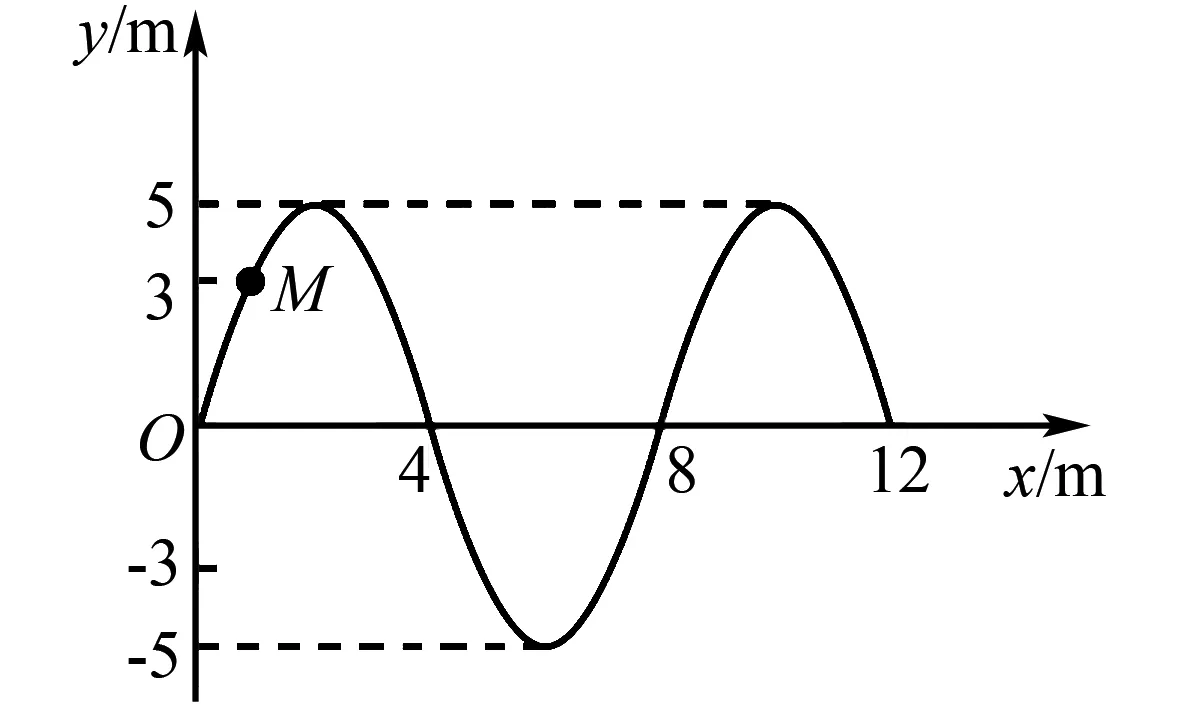
圖4

A．此后再經6 s該波傳播到x=24 m處

B．M點在此后第3 s末的振動方向沿y軸正方向

C．波源開始振動時的運動方向沿y軸負方向

D．此后M點第一次到達y=-3 m處所需時間是2 s

對于A、B、C選項這里不再重復，較易得到AB正確.對于D選項，以下是筆者列出學生錯解過程供參考.

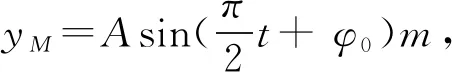
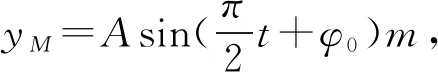
當機械波中質點某時刻處于波峰、波谷或平衡位置時，這類型題學生撐握起來比較容易，但質點不處于上述位置時，運用“相位差”求解這類疑難問題是一種符合學生認知的好方法.通過課堂教學實踐，絕大部分學生能很快理解并應用，以上是筆者教學中的一點體會.