秒解“動態平衡問題”的技巧

熊高云

(江西省南康中學北校區 341400)

1 “一恒一定向”

“一恒一定向”即為物體所受的三力中有一個力恒定，一個力的方向恒定.如圖1所示，OA、OB、OC為三根細繩，保持O點不動，B繩順時針旋轉，分析兩繩中的拉力變化情況？

圖1 圖2

(1)常規解法—圖解法，對O點受力分析如圖2所示.

觀察圖形可知，B繩的拉力先減小后增大，A繩中的拉力一直減小.

(2)方法升級理解(口決：不轉的力隨方向變化的兩力的夾角增大而增大，減小而減小，當方向變化的兩力垂直時轉動的力最小，往兩邊都增大)

認真分析可知，隨著B繩順時針旋轉，兩繩的夾角減小，同時觀察A繩的力也在減小，而當B繩也A繩垂直時，B繩中的拉力最小，所以可以得到規律，A繩的拉力(即不轉的力)隨兩繩夾角的增大而增大(或夾角的減小而減小)，B繩的拉力(轉動的力)在B繩也A繩垂直時最小，只要分析B繩轉動過程中會不會出現垂直即可判斷，用此方法則不用畫三角形而快速解決此類問題.

例1如圖3所示，把一個光滑圓球放在兩塊擋板AB和AC之間，AB與AC之間的夾角為30°．現將AC板固定，而使AB板沿順時針方向緩慢轉動90°，則( ).

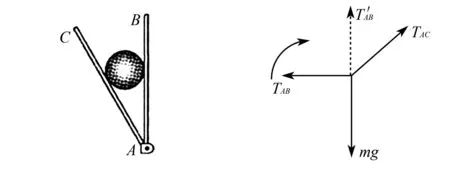
圖3 圖4

A.球對AB板的壓力逐漸減小

B.球對AB板的壓力先減小后增大

C.球對AC板的壓力逐漸增大

D.球對AC板的壓力先減小后增大

解析畫出小球的受力如圖4

由題意可知TAB從水平方向轉到豎直方向，TAB與TAC夾角一直減小，則不轉的力TAC一直減小，TAB在轉動過程中一定經歷與TAC垂直的位置，垂直時最小，則TAB先減小后增大，故選B.

2 “兩變力恒定夾角”

“兩變力恒定夾角”即為兩個變力的夾角恒定，如圖5所示，三根細繩連接同一點O，且在C繩上吊一個重物，保持A、B繩夾角α不變，A、B兩繩順時針轉動30°過程中，A、B繩上的拉力變化情況？

圖5 圖6

(1)常規解法——“拉密定理”，如圖6

由“拉密定理”可知

(2)方法升級理解(口決：“對角垂直時拉力最大”)

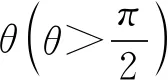
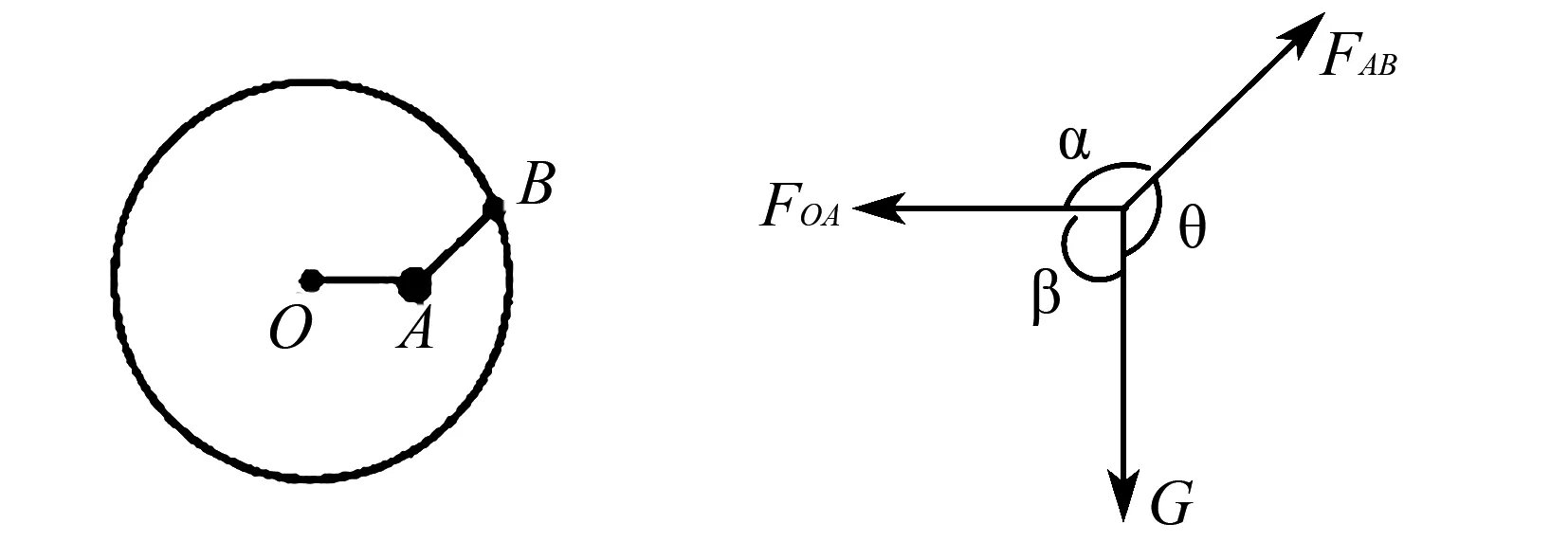
圖7 圖8

A.OA上的張力逐漸增大

B.OA上的張力先增大后減小

C.AB上的張力逐漸增大

D.AB上的張力先增大后減小

解受力分析如圖8

在轉動過程中β從90°→180°，由對角垂直時拉力最大可知，FAB一直減小，同理θ從鈍角變成銳角，其間一定經歷直角的狀態，由對角垂直時拉力最大可知，FOA先增大后減小，故選B.

3 “大Y模型”

“大Y模型”即為晾衣服模型，如圖9所示，一根細繩A、B兩端分別栓在兩根固定的桿上，兩桿間的距離為d，重物的重力為G

圖9 圖10

(1)常規解法：

對O點受力分析如圖10所示

由平衡可知

2Tcosα=G

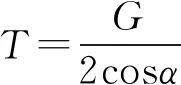
由幾何關系可知LOAsinα+LBOsinα=d

根據題意逐步分析解答.

(2)方法升級理解(口決：“近小遠大，縱不變”)

分析總結規律

①縱移，即A點或B點上、下移動時，由于d不變，繩長不變，則α不變，則繩中拉力不變；

②遠離，即兩桿距離增大，α變大，繩中拉力變大;

③靠近，即兩桿距離減小，α變小，繩中拉力變小；

口決：對于α和T的變化情況滿足：“近小遠大，縱不變”，其中“近”和“遠”指的是距離d，d小，α小，繩中拉力小；d大，α大，繩中拉力大，“縱”指的是A點或B點上、下移動，此時繩中拉力不變.

例3(2017·天津·高考真題)如圖11所示，輕質不可伸長的晾衣繩兩端分別固定在豎直桿M、N上的a、b兩點，懸掛衣服的衣架鉤是光滑的，掛于繩上處于靜止狀態．如果只改變一個條件，當衣架靜止時，下列說法正確的是 ( ).

圖11

A．繩的右端上移到b′，繩子拉力變小

B．繩的兩端高度差越小，繩子拉力越大

C．將桿N向右移一些，繩子拉力變大

D．若換掛質量更大的衣服，則衣服架懸掛點右移

解ABC.利用口決：“近小遠大，縱不變”可知，繩的右端上移到b′，即為縱移，則繩子拉力不變，將桿N向右移一些，即遠離，則繩子拉力變大，繩的兩端高度差越小，即縱移，則繩子拉力不變，故AB錯誤，C正確；D．若換掛質量更大的衣服，仍然平衡，則位置不變，只是繩子拉力變大，故D錯誤.