極限思維厘清人造衛星的發射、運行與環繞

霍良平

(陜西省安康市旬陽第二中學 725741)

極限思想是用極限概念分析、解決實際問題的思維加工過程，是一種科學思維方法.借助極限思想，我們能從有限認識無限，從"不變"認識"變"，從直線認識曲線，從量變認識質變，從近似認識精確.極限問題的物理思想是物理過程量的連續漸變累積；極限問題的數學思想是微積分.人造衛星發射、運行與環繞的理論探究是學生開啟航空航天大門的鑰匙，如果在教學過程中只引導學生對人造地球衛星軌道環繞完成公式推理應用，而對人造衛星的發射及其環繞前的運行過程少有分析，這樣的物理課堂只是做了物理知識教學；如果借助人造衛星的教學幫助學生開鎖航空航天的的好奇心與理論技能，這樣的物理課堂是做好物理教育.

1 極限放大思想造“人造衛星”

以水平拋出的粉筆為例.粉筆以初速度v0沿水平拋出，不計空氣阻力，粉筆做平拋運動.學生分析完成平拋運動的規律：

水平方向：

X=v0t

豎直方向：

師：保持粉筆拋出時的高度不變，如果不斷增大拋出時的初速度v0，平拋運動的水平位移X會怎么變化？

生：會不斷增大

師：如果v0足夠大，請同學們大膽猜想水平位移會……

生：水平位移指向無限遠，平拋運動的曲線運動趨近沿水平方向的直線運動，即粉筆回不到地球上.

師：如果你擁有和這只粉筆一樣大的速度v0，并隨拋出的粉筆方向沿地面跟著粉筆走，以你為參考系，粉筆做什么運動？

生：靜止

師：你繞地球走了一圈，粉筆呢？

生：粉筆繞地球轉了一圈，哦，粉筆做勻速圓周運動.

師：同學們，此時的粉筆就不叫粉筆啦，物理學家把它叫人造衛星！

受平拋運動到圓周運動的極限思維啟發，平拋運動可以看做是近心運動：即重力提供以速度為v0，半徑近似等于地球半徑R的圓周運動所需要的向心力有多余，多余的這部分重力使粉筆做豎直方向的加速直線運動，即平拋運動是勻速圓周運動和豎直方向加速直線運動的合運動.重力的作用效果分為兩部分：

兩個分運動的運動類型：勻速圓周運動和加速直線運動.

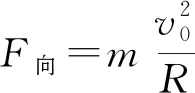
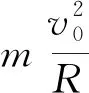
得出人造衛星成果發射的最小速度

2 極限思想造“脫軌”人造衛星

建構衛星發射模型：如圖1所示，衛星在地面附近一次性加速獲得初速度v0，進入高空軌道做勻速圓周運動.衛星離開地面的初速度v0與水平方向之間的夾角越大，衛星飛行的高度就越高.極限思維：當h趨向無窮大時，衛星從地面上發射的最小初速度v0是多少？

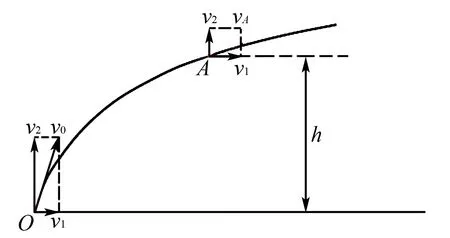
圖1

(G=6.67×10-11N·m2/kg2,M=5.96×1024kg,R=6.37×106m.)

理論分析：無窮遠處的引力趨于零，無法提供做圓周運動所需的向心力.即無窮遠高度處不能做圓周運動，取速度等于零，衛星初始動能就等于克服引力對衛星做的功.

(當α趨近90°時，v2=v0)

聯立兩式得：

v0=v2=11.2 km/s

當發射速度大于11.2 km/s，即該物體不再是地球的人造衛星.

故人造衛星的發射速度7.9 km/s≤v0≤11.2 km/s.

3 極限理論推理地球同步衛星的發射速度和發射角

以地球同步衛星為例，如圖1，設初速度v0與水平方向成α角，同步衛星要上升至距地面高度為h0的高空做勻速圓周運動，線速度為v1，求同步衛星的發射速度？

(已知：G=6.67×10-11N·m2/kg2,M=5.96×1024kg,R=6.37×106m，h0=3.6×107m,ω地=7.29×10-5rad/s)

綜合分析：同步衛星在距離地面高度為h0過A位置的面內以線速度v1，半徑為R+h0做勻速圓周運動，此高度處的v′2=0，衛星受到的吸引力全部提供向心力，即

①

v1=(R+h0)ω地

②

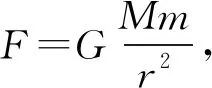
③

④

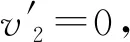
⑤

人造衛星發射速度

⑥

聯立②⑤⑥式得

v0=8.5km/s

⑦

人造衛星的發射角

⑧

聯立②⑦⑧式得

α≈68.65°

⑨