反例教學(xué)法在高中數(shù)學(xué)教學(xué)中的應(yīng)用

江蘇省梁豐高級中學(xué)

施冬芳

美國數(shù)學(xué)家蓋爾鮑姆提出：“數(shù)學(xué)由證明和反例構(gòu)成，并朝著證明與反例構(gòu)造發(fā)展.”反例是指通過變換事物的屬性，引發(fā)思辨，從反面凸顯出事物的本質(zhì)屬性的例證.證明是通過已知為真來確定某一事物的真實(shí)性，反例則是用已知為真揭露另一個判斷是虛假的，兩者的目的都是為了揭露事物的本質(zhì)屬性，它們呈相輔相成的關(guān)系.

新課標(biāo)明確提出：“數(shù)學(xué)教學(xué)應(yīng)用實(shí)例進(jìn)行合情推理，讓學(xué)生在猜測、探索、演繹推理中確定結(jié)論的正確性，或構(gòu)造反例來駁回錯誤的猜想.”反例的構(gòu)造能凸顯概念及定理的本質(zhì)特征，讓學(xué)生在反思中發(fā)現(xiàn)錯誤，加深對知識的理解與掌握程度；同時，構(gòu)造反例還可打開學(xué)生的逆向思維，幫助學(xué)生從反面理解所學(xué)知識，培養(yǎng)學(xué)生解決問題的能力.

1 反例法在分類討論中的應(yīng)用

任何一個結(jié)論的成立都離不開一定條件的輔助，每種數(shù)學(xué)思想方法的應(yīng)用也有其相應(yīng)的范圍.高中數(shù)學(xué)相對復(fù)雜，不少問題的結(jié)論并不唯一，分析時需根據(jù)問題的特點(diǎn)，從若干類出發(fā)，將一個大問題轉(zhuǎn)化為一個個小問題.這種根據(jù)實(shí)際情況分類，再逐個突破研究的數(shù)學(xué)思想就是常見的分類討論思想.

然而，當(dāng)我們遇到的命題似真似假時，利用反證法常會出現(xiàn)分類不全或假設(shè)錯誤，導(dǎo)致解題失敗.而反例的構(gòu)造，則能凸顯問題的本質(zhì)，快速解決問題.解題中，學(xué)生常會遇到一些問題無法直接求解，此時巧妙地從問題的反面進(jìn)行分析，可使問題變得更加簡單.

例1已知關(guān)于x的方程x2+2ax+2a2-1=0至少有一個負(fù)實(shí)數(shù)根，則實(shí)數(shù)a的取值范圍是什么？

解析：此題若從正面來論證，需分別從三種情況來分析.①存在兩個負(fù)實(shí)數(shù)根；②正、負(fù)實(shí)數(shù)根各一個；③存在一個零根，一個負(fù)實(shí)數(shù)根.

若分別討論以上三種情況，不僅過程繁瑣、冗長，還容易出現(xiàn)失誤.本題若構(gòu)建反例，設(shè)方程無負(fù)實(shí)數(shù)根時實(shí)數(shù)a的范圍為A，則方程至少有一個負(fù)實(shí)數(shù)根時a的范圍即為A的補(bǔ)集.

點(diǎn)評：本題若從正面論證，需耗費(fèi)大量的時間與精力，而從反例的角度去分析，則使繁雜的問題變得簡捷很多.因此，遇到分類討論的問題時，不要受思維定式的影響，應(yīng)從多角度去思考、分析問題，必要的情況下通過反例的構(gòu)造，能讓冗長的問題變得短小、精煉.

2 反例法在概念教學(xué)中的應(yīng)用

高中數(shù)學(xué)概念比較抽象，有些學(xué)生在學(xué)習(xí)概念時不得法，憑借死記硬背來掌握概念，因?qū)Ω拍畹膬?nèi)涵缺乏深刻理解，而導(dǎo)致在概念的表達(dá)或應(yīng)用時錯誤百出.倘若在概念形成的教學(xué)階段，能讓學(xué)生從深層次剖析概念的內(nèi)涵，辨析常見錯誤產(chǎn)生的原因，則能幫助學(xué)生從反面或側(cè)面挖掘出概念的本質(zhì)，建構(gòu)完整的認(rèn)知.將反例法應(yīng)用到概念教學(xué)中，對一些基礎(chǔ)薄弱的學(xué)生而言，能改變他們所存在的概念模糊或認(rèn)識不完整的狀況.

比如，對韋達(dá)定理的認(rèn)識，學(xué)生的思維受原有認(rèn)知經(jīng)驗(yàn)的束縛，常認(rèn)為兩根之和為一次項(xiàng)系數(shù)的相反數(shù)，兩根的積為常數(shù)項(xiàng).妥妥地忽略了定理中一個很重要的條件：平方項(xiàng)的系數(shù)未必是1.

這是一個可以避免的錯誤，教師在教學(xué)時，可向?qū)W生提出：ax2+bx=c=0兩根的和是-b，積為c，這種說法對嗎？

若學(xué)生認(rèn)為這種說法是錯誤的，教師就趁機(jī)追問，錯在哪兒？

通過反例的構(gòu)造，不僅能彌補(bǔ)學(xué)生思維中對韋達(dá)定理認(rèn)識不全的問題，還能讓學(xué)生對概念學(xué)習(xí)產(chǎn)生新的認(rèn)識，為后期的學(xué)習(xí)奠定基礎(chǔ).

3 反例法在錯題教學(xué)中的應(yīng)用

教學(xué)中，不少學(xué)生受慣性思維的影響，解題時會想當(dāng)然地按照自己的意愿給出相應(yīng)的結(jié)論.為了避免思維定式帶來的副作用，教師可引導(dǎo)學(xué)生在適當(dāng)?shù)臅r候應(yīng)用反例，激發(fā)學(xué)生的認(rèn)知沖突，通過矛盾的解決來獲得問題的本質(zhì).

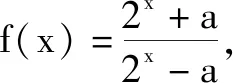
不論f(0)=0還是f(-x)=-f(x)的計(jì)算，這些錯誤發(fā)生的關(guān)鍵性因素，還是因?yàn)閷W(xué)生對于奇函數(shù)的定義沒有達(dá)到深刻理解的程度，對f(0)=0的適用范圍沒有產(chǎn)生足夠的認(rèn)識.為了讓學(xué)生找到錯誤產(chǎn)生的根源，避免此類問題的再次發(fā)生，筆者構(gòu)造了反例問題，達(dá)到幫助學(xué)生糾錯，提升思維的作用.

問題(1)a=1是怎么得到的？(根據(jù)f(0)=0得來.)

(2)是不是奇函數(shù)就一定有f(0)=0？(f(x)是奇函數(shù)時，f(-x)=-f(x)?f(-x)+f(x)=0，f(0)=0.)

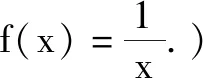
(4)回顧第(2)個問題，來分析另一個學(xué)生的答案.(函數(shù)f(x)定義域?yàn)镈，如果0∈D，根據(jù)f(0)=0可以得到a=1；如果0?D，根據(jù)20+a=0?a=-1；也可以利用特殊值f(1)+f(-1)=0?a=±1.)

通過以上環(huán)環(huán)相扣的問題，容易發(fā)現(xiàn)，函數(shù)f(x)定義域?yàn)镈，如果0∈D，就一定存在f(0)=0；而0?D，f(x)為奇函數(shù)時，就一定存在20+a=0，a=-1.

隨著設(shè)問、追問，以及反例的應(yīng)用，學(xué)生經(jīng)歷了探究錯誤根源的過程，并在不斷的思考、分析與推理中更進(jìn)一步理解問題的本質(zhì).

正例與反例是相互對立又統(tǒng)一的關(guān)系，教學(xué)中若想單純地憑借正例解決一切問題，這是不現(xiàn)實(shí)的.很多時候，反例能襯托出知識的核心，讓不易發(fā)現(xiàn)的錯誤暴露于學(xué)生的思維中.因此，筆者常將反例法應(yīng)用到錯題教學(xué)中，以激活學(xué)生的思維，幫助學(xué)生提煉知識，達(dá)到融會貫通的目的.

4 反例法在特殊情況中的應(yīng)用

特殊與一般是相互對立又相互依賴的關(guān)系，有些問題可把它們的特殊情形作為突破口，從獨(dú)特的性質(zhì)或變化規(guī)律中，找出解題途徑，實(shí)現(xiàn)從特殊中發(fā)現(xiàn)一般的規(guī)律，又用特殊來否定一般的目的.因此，將反例應(yīng)用于特殊情況中，是實(shí)現(xiàn)問題突破的重要方法之一.

例3判斷正誤：如果函數(shù)f(x)與其反函數(shù)f-1(x)的圖象存在交點(diǎn)，那么此交點(diǎn)一定在直線y=x上.

面對此題，若從正面去判斷比較麻煩，而反例的應(yīng)用，則能使判斷過程變得清晰，簡潔.本題若用“函數(shù)y=-x”作為反例，即可判斷，問題也就得以解決.但不少學(xué)生遇到此題時，并不能一下子就想到用反例法，這就需要教師在日常教學(xué)中多加引導(dǎo)，讓學(xué)生有更多機(jī)會接觸到類似的問題.如此，對培養(yǎng)學(xué)生的創(chuàng)新意識與逆向思維具有深遠(yuǎn)的影響.

其實(shí)，反例教學(xué)法除了應(yīng)用于以上幾種情況，還有更多、更廣泛的應(yīng)用范圍，在此就不一一舉例說明，但它對數(shù)學(xué)教學(xué)的重要影響有目共睹.教學(xué)中，教師應(yīng)引導(dǎo)學(xué)生在恰當(dāng)?shù)臅r候，靈活應(yīng)用反例，以增強(qiáng)學(xué)生對知識的理解，提高解題能力的同時形成良好的數(shù)學(xué)思想.

總之，反例教學(xué)法對數(shù)學(xué)概念、定義、解題等教學(xué)具有重要影響.它能提高學(xué)生對謬誤的識別能力，錘煉學(xué)生的數(shù)學(xué)思維，為抽象邏輯思維與逆向思維的發(fā)展奠定基礎(chǔ)，還能幫助學(xué)生形成辯證統(tǒng)一的思維品質(zhì)，為學(xué)生的可持續(xù)性發(fā)展與數(shù)學(xué)核心素養(yǎng)的形成夯實(shí)基礎(chǔ).