重視核心素養(yǎng) 凸顯數(shù)學(xué)本質(zhì)
——以2022年新高考數(shù)學(xué)Ⅰ卷為例

江蘇省如東高級(jí)中學(xué)

葛張勇

“2022年高考數(shù)學(xué)落實(shí)立德樹(shù)人的根本任務(wù)，促進(jìn)學(xué)生德智體美勞全面發(fā)展，體現(xiàn)高考改革的要求.”教育部教育考試院命題專(zhuān)家對(duì)今年高考數(shù)學(xué)試題進(jìn)行了評(píng)價(jià).同時(shí)指出，試卷在考查學(xué)生基礎(chǔ)知識(shí)和學(xué)科能力的同時(shí)，尤其突出對(duì)數(shù)學(xué)核心素養(yǎng)和學(xué)習(xí)能力的考查，體現(xiàn)了很好的選拔功能.

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017版2020修訂)》指出：“引導(dǎo)教學(xué)更加關(guān)注育人目的，更加注重培養(yǎng)學(xué)生核心素養(yǎng)，更加強(qiáng)調(diào)提高學(xué)生綜合應(yīng)用數(shù)學(xué)知識(shí)解決實(shí)際問(wèn)題的能力，把握教學(xué)的深度和廣度，為階段性評(píng)價(jià)、學(xué)業(yè)水平測(cè)試和升學(xué)考試命題提供重要依據(jù).”下面以2022年全國(guó)新高考數(shù)學(xué)Ⅰ卷為例，談?wù)勑赂邤?shù)學(xué)試卷核心素養(yǎng)的考查，旨在拋磚引玉.

1 重視本質(zhì)，把握數(shù)學(xué)抽象的思維方式

數(shù)學(xué)抽象是根據(jù)研究對(duì)象的數(shù)量及圖形關(guān)系，結(jié)合已有的數(shù)學(xué)知識(shí)抽象出數(shù)學(xué)概念及數(shù)學(xué)模型，進(jìn)而用數(shù)學(xué)知識(shí)、數(shù)學(xué)思維分析解決問(wèn)題.其抽象方法有性質(zhì)抽象、關(guān)系抽象、變換抽象、類(lèi)比抽象等，數(shù)學(xué)抽象是數(shù)學(xué)產(chǎn)生和發(fā)展的思維基礎(chǔ)，凸顯了數(shù)學(xué)本質(zhì).

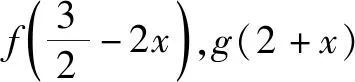
C.f(-1)=f(4) D.g(-1)=g(2)

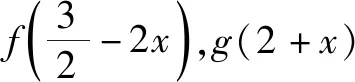
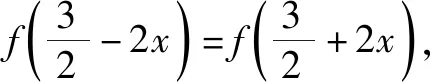
所以g(-1)=g(1)=-g(2)，故選項(xiàng)D錯(cuò)誤；

若函數(shù)f(x)滿足題設(shè)條件，則函數(shù)f(x)+C(C為常數(shù))也滿足題設(shè)條件，所以無(wú)法確定f(x)的函數(shù)值，故選項(xiàng)A錯(cuò)誤. 故選：BC.

解法二：化抽象為具體，令函數(shù)f(x)=sin πx+1，則g(x)=πcos πx，符合題意.故選：BC.

點(diǎn)評(píng)：解法一的關(guān)鍵是轉(zhuǎn)化題干條件為抽象函數(shù)的性質(zhì)，準(zhǔn)確把握原函數(shù)與導(dǎo)函數(shù)圖象間的關(guān)系，把握函數(shù)的奇偶性等性質(zhì)(必要時(shí)結(jié)合圖象)即可得解；解法二是從一般到特殊.

2 歸納演繹，培養(yǎng)邏輯推理的探索品質(zhì)

邏輯推理是指借助問(wèn)題的條件以及數(shù)學(xué)概念、定理，通過(guò)條件之間的關(guān)聯(lián)從而得到新的結(jié)論或者新的命題.它包括從特殊到一般以及從一般到特殊兩類(lèi)推理方式，是數(shù)學(xué)學(xué)習(xí)中不可缺少的一種素養(yǎng).

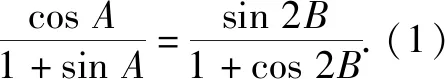
點(diǎn)評(píng):三角函數(shù)化簡(jiǎn)的核心邏輯是“化同”，即角的“化同”和函數(shù)名的“化同”.既要知道公式、定理、解法是什么，還要知道解題的動(dòng)機(jī)和時(shí)機(jī)、解題邏輯是什么，以邏輯馭解法，以解法促邏輯.

3 創(chuàng)設(shè)情境，構(gòu)建數(shù)學(xué)建模的應(yīng)用意識(shí)

數(shù)學(xué)建模是根據(jù)所學(xué)數(shù)學(xué)知識(shí)解決實(shí)際問(wèn)題的素養(yǎng)，它是數(shù)學(xué)抽象、邏輯推理、數(shù)據(jù)分析和運(yùn)算等其他核心素養(yǎng)的集中體現(xiàn)和升華.數(shù)學(xué)建模通常包括模型分析、模型建立、模型求解、模型檢驗(yàn)等步驟.

A.1.0×109m3B.1.2×109m3

C.1.4×109m3D. 1.6×109m3

解析:依題意可知棱臺(tái)的高為MN=157.5-148.5=9(m)，所以增加的水量即為棱臺(tái)的體積V.

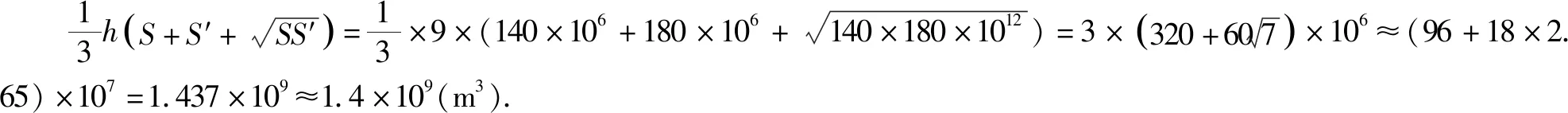
故選：C.

點(diǎn)評(píng):本題建模容易.兩點(diǎn)易錯(cuò)，一是棱臺(tái)的體積公式，二是棱臺(tái)的高與什么關(guān)系最密切.在題干的提示下估算還可以優(yōu)化估算的次數(shù).《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017版2020修訂)》第27頁(yè)明確提出，知道球、棱柱、棱錐、棱臺(tái)的表面積和體積的計(jì)算公式，能用公式解決簡(jiǎn)單的實(shí)際問(wèn)題.

4 數(shù)形結(jié)合，提升直觀想象轉(zhuǎn)化能力

《新課程課程標(biāo)準(zhǔn)》指出:“直觀想象是指借助幾何直觀和空間想象感知事物的形態(tài)與變化，利用空間形式特別是圖形，理解和解決數(shù)學(xué)問(wèn)題的素養(yǎng).”直觀想象的素養(yǎng)體現(xiàn)的是數(shù)形結(jié)合的重要數(shù)學(xué)思想.以形助數(shù)，挖掘圖形性質(zhì)，是高考數(shù)學(xué)常見(jiàn)的優(yōu)化運(yùn)算策略.

例4(2022年新高考Ⅰ卷第14題)寫(xiě)出與圓x2+y2=1和(x-3)2+(y-4)2=16都相切的一條直線的方程.

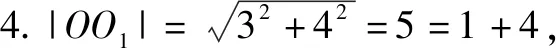
圖1

點(diǎn)評(píng):本題挖掘圖形性質(zhì)，優(yōu)化解題策略.教學(xué)中引導(dǎo)學(xué)生探索數(shù)學(xué)知識(shí)的幾何背景，增強(qiáng)運(yùn)用幾何直觀解決問(wèn)題的意識(shí)，提高學(xué)生數(shù)形結(jié)合解決問(wèn)題的能力，從而提升直觀想象的核心素養(yǎng).考場(chǎng)上處理此類(lèi)開(kāi)放性試題選擇一個(gè)最簡(jiǎn)單結(jié)果即可.

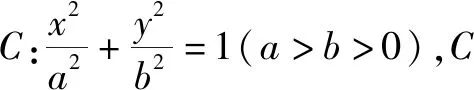
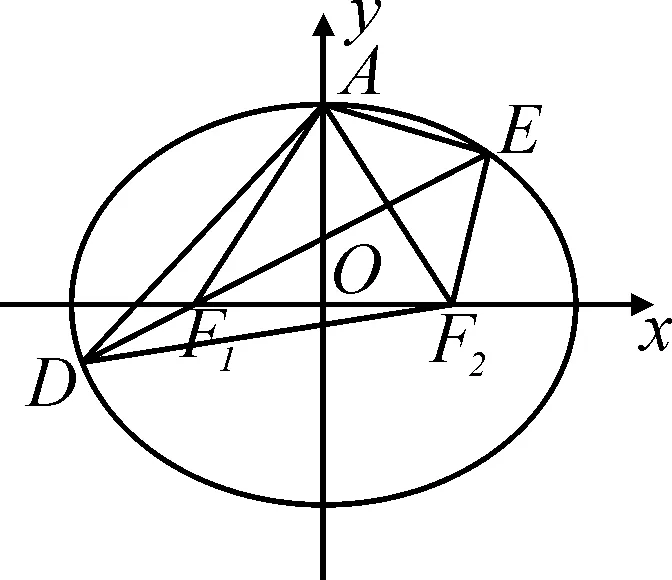
圖2

點(diǎn)評(píng):本題的幾何法，即對(duì)稱(chēng)性+橢圓定義將挖掘圖形幾何性質(zhì)體現(xiàn)得淋漓盡致.

5 數(shù)據(jù)分析，助力數(shù)學(xué)運(yùn)算的核心素養(yǎng)

數(shù)據(jù)分析是從研究對(duì)象中獲取關(guān)鍵數(shù)據(jù)，應(yīng)用數(shù)學(xué)方法對(duì)數(shù)據(jù)進(jìn)行量化分析，形成研究對(duì)象的定量分析結(jié)果.數(shù)據(jù)分析是研究隨機(jī)現(xiàn)象的重要數(shù)學(xué)技術(shù)，與數(shù)學(xué)抽象、數(shù)學(xué)建模、邏輯推理、數(shù)學(xué)運(yùn)算等核心素養(yǎng)之間密不可分.

數(shù)學(xué)運(yùn)算是六大核心素養(yǎng)中極其重要的一個(gè)，在數(shù)學(xué)學(xué)習(xí)中起著重要作用，它是解決數(shù)學(xué)問(wèn)題的重要手段.數(shù)學(xué)運(yùn)算不是簡(jiǎn)單的數(shù)學(xué)計(jì)算，它反映了一定的綜合能力，需要在解決問(wèn)題中確定運(yùn)算目標(biāo)，探究運(yùn)算思路，設(shè)計(jì)運(yùn)算程序，依據(jù)運(yùn)算法則正確解答.

(1)求l的斜率；

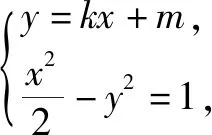
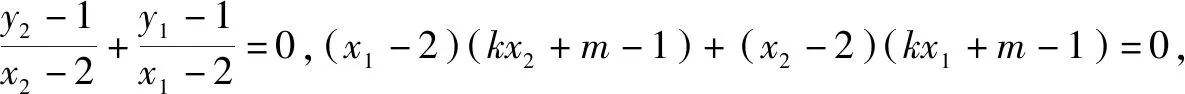
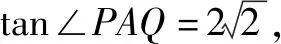
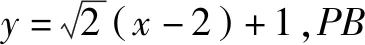
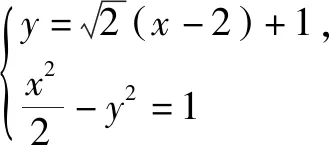
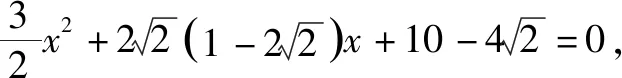
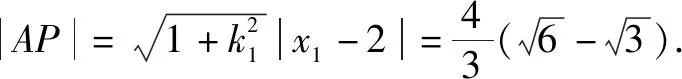
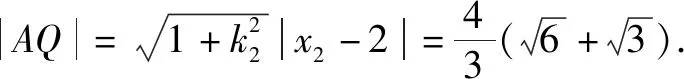
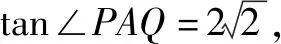
點(diǎn)評(píng):無(wú)運(yùn)算不數(shù)學(xué)，數(shù)學(xué)運(yùn)算是解決數(shù)學(xué)問(wèn)題的關(guān)鍵環(huán)節(jié).高考對(duì)數(shù)學(xué)運(yùn)算要求越來(lái)越高.本題無(wú)論用什么方法解決，較復(fù)雜的運(yùn)算都不可避免.教師在教學(xué)中既要注重解題思路、方法的探究和設(shè)計(jì)，也要在具體運(yùn)算過(guò)程中做示范和引領(lǐng)，幫助學(xué)生感受反思解題運(yùn)算的方法和技巧，優(yōu)化解題運(yùn)算，培養(yǎng)學(xué)生處理數(shù)學(xué)運(yùn)算的耐心、細(xì)心及必勝的信心.