基于改進蟻群算法的打磨機器人路徑規劃

蔡改貧，陳永康，周小云，李宇達，曾常熙

(江西理工大學機電工程學院，江西贛州 341000)

0 前言

打磨機器人是從事打磨加工的工業機器人，在機器人的末端安裝抓取工具，進行運動控制，使抓取的工件可以到達并固定于刀具的特定位置，根據工件打磨形狀的需要，機器人抓取工件進行相應的軌跡運動，完成工件弧形曲面的加工。打磨機器人路徑規劃目的是在空間環境中按照一定的規則，規劃出由起點到終點用時最短或最光滑的路徑，有利于深入研究機器人應用領域。

自20世紀以來，路徑規劃技術的研究已經取得了許多重要成果。許多二維路徑規劃建模方法沿用至今，如網格法、拓撲法、可見圖法等。隨著軌跡規劃領域不斷發展，出現了更多復雜的路徑規劃算法，如Dijkstra算法、Prim算法、模擬退火算法、蟻群算法、A算法、人工勢場法和模糊邏輯控制算法，它們在工程實踐中得到了廣泛應用。其中，蟻群算法是一種分布式智能仿生算法，主要模擬蟻群在尋找食物過程中協同合作搜尋最佳路徑的過程，搜尋過程具有正反饋性、并行性及較強的魯棒性等優點。蟻群算法已廣泛應用于車間調度、旅行規劃、網絡路由、機器人路徑規劃、電力系統、聚類分析、數據挖掘和圖像處理等領域。在機器人路徑規劃領域，LEE等利用遺傳算法優化蟻群算法參數，實現動態路徑規劃。邱莉莉和鄭建立改進信息素初始化和狀態轉移概率，但該方法只能降低螞蟻陷入死鎖的可能性，不能完全避免死鎖的發生。趙華東等提出相應的死角表，當螞蟻陷入死鎖時，可以使用罰函數來更新軌跡。

基于以上分析，根據打磨機器人工作方法的有效性和實時性的要求，針對具體打磨機器人的構型，對機器人進行D-H建模分析，再進行運動學分析與驗證。針對路徑規劃問題，通過改進蟻群算法的信息素更新方法，將新的自適應計算方法應用于狀態轉移規則中，并通過引入阻尼系數改進啟發式信息函數，在MATLAB中進行模擬實驗，尋找到一條最優路徑，驗證該方法的可行性。

1 打磨機器人運動學分析

1.1 正運動學模型分析

當需要確定機器人在空間中的位置關系時，可以在機械手的三維空間中固定一個坐標系，然后分析該坐標系的原點位置與、、軸的位置關系，即建立D-H坐標系，分析得出各個連桿D-H參數；從第一個關節開始依次進行變換，直到最后一個關節被確定，這樣就確定了機械手的總變換矩陣。圖1所示為打磨機器人結構簡圖，圖中右側為打磨刀具。

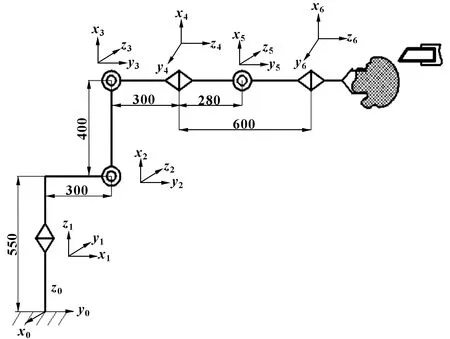
圖1 打磨機器人模型簡圖

各關節D-H參數如表1所示。

表1 各關節D-H參數

(=1,2,…,6)表示各個關節的D-H矩陣，則得出運動學方程如下：

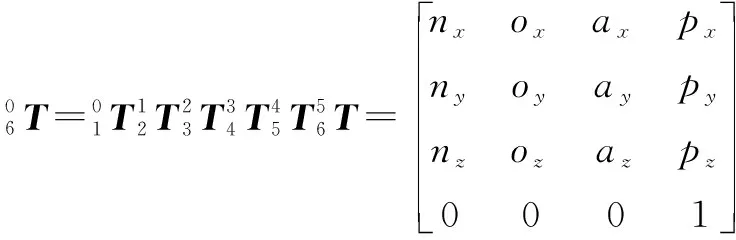
(1)

其中：、、分別表示機械手末端坐標系的3個坐標軸上的單位向量投影到基座坐標系的方向余弦;表示末端坐標原點在基座坐標系的坐標值。

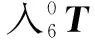
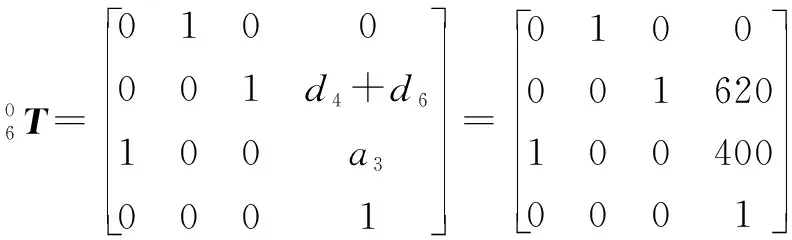
(2)

1.2 逆運動學分析

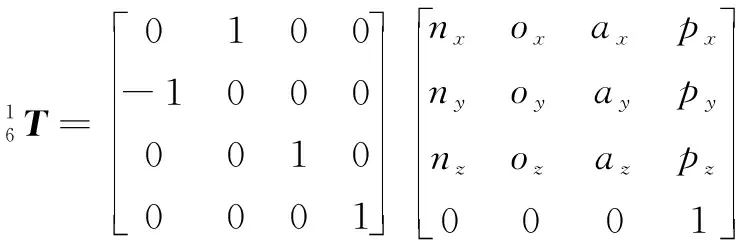
(3)

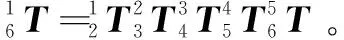
(4)

其中：

=sin=cos

=-[(+)-(-)]-

(-)

=[(+)-(-)]-

(-)

=-(+)-(-)

=-(+)-[(+)+

(-)]

=(+)-[(-)+

(+)]

=[(-)+(+)]+

(+)

=(+)-(-)

=--(-)-[(-)-

(+)]

令式(4)左右兩邊(2,3)和(2,4)元素對應相等，則有-=和-=。解該方程組得tan=(-)(-)，得的表達式為

=arctan[(-)(-)]

(5)

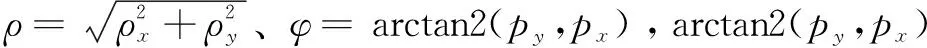
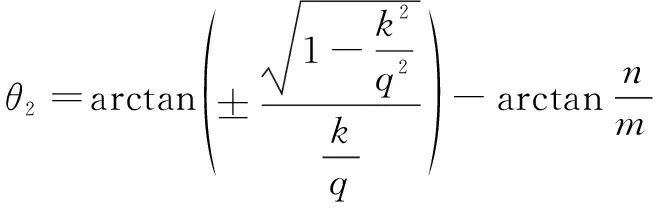
(6)

=-=

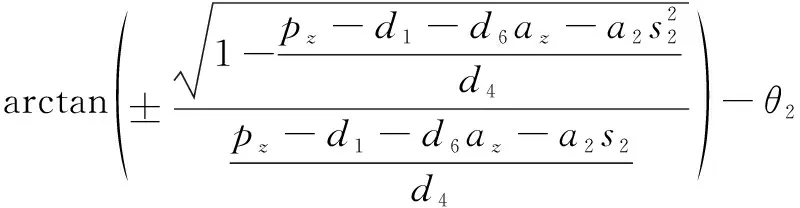
(7)

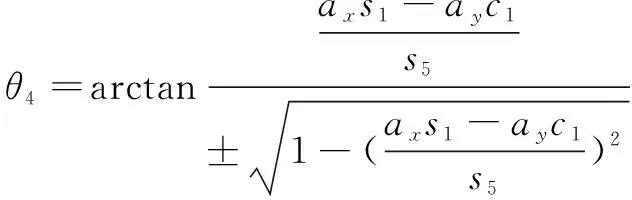
(8)

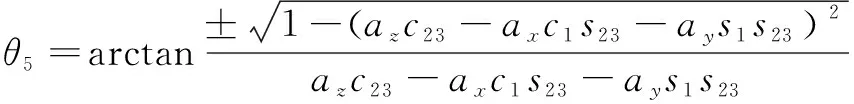
(9)

(10)

其中：

=sin(+)=cos(+)

=++-+

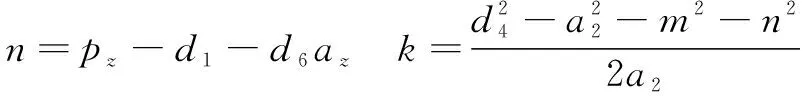
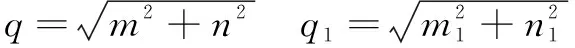
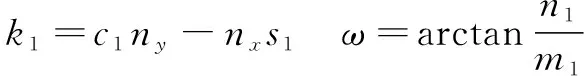
=cos==sin=

驗證過程：設連桿參數=300 mm、=320 mm、=400 mm，并設6個關節角度均為30°，從而由運動方程求解得：

(11)

則可得、、、、、、、、、、、，將各數據代入各關節角度表達式，使用MATLAB得計算結果：=30004 9°、=30010 3°、=20931 3°、=29999 8°、=30006 4°、=30006 6°。

2 改進蟻群算法的路徑規劃

2.1 三維環境建模

路徑規劃中傳統的環境建模方法包括可視圖法、單元樹法和二維柵格法，此類柵格法可推廣到三維空間中。本文作者采用山峰式環境模型模擬機器人工作環境，將真實的機器人三維環境用抽象的山峰圖形表示。為簡化蟻群算法路徑規劃，以機器人自身基坐標系為基礎，建立環境模型坐標系-。

實驗環境是Window 10系統、MATLAB 2016a、RobotStudio6.0、英特奔騰CPU 1.70 GHz,內存12 GB,64位操作系統。圖2所示為機器人工作環境，將工作空間中的其他設備與障礙物以山峰代替。如圖3所示，在MATLAB 2016a中繪制立體抽象的山峰圖形模擬機器人的工作環境。(0～100 km)軸表示經度方向距離，(0～100 km)軸表示緯度方向距離，(0～2 500 m)軸表示海拔高度。地形中的非平面部分可以理解為障礙物，凸起的曲面障礙物為斜坡，凹陷的曲面障礙物為溝渠。

圖2 機器人工作環境

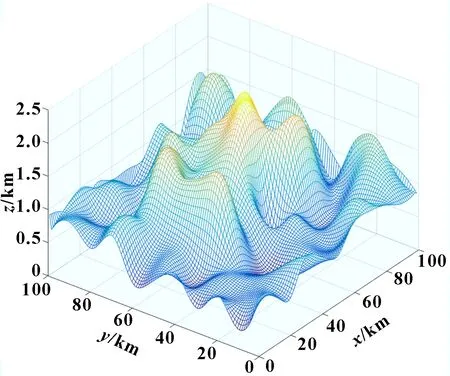
圖3 三維環境模型

2.2 蟻群算法介紹

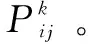
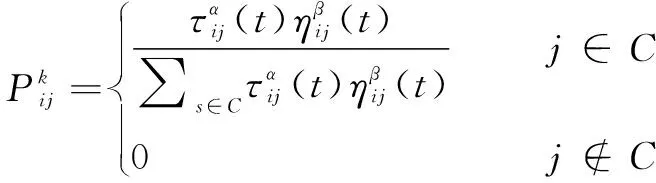
(12)

其中:是下一節點集合；()是路徑(，)的信息素值；是信息素激勵因子;是期望的啟發式因子。啟發式因子計算公式：

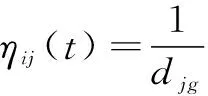
(13)

式中：為節點到目標節點的歐氏距離。

局部信息素會在螞蟻搜尋下一個節點時進行更新：

(+1)=(1-)()

(14)

式中:()表示信息素在離散點(，，)上的濃度值；表示更新的次數；(0<<1)為全局信息素更新系數。

2.3 改進蟻群算法

利用蟻群算法進行路徑規劃時，要找到全局最優路徑，搜索空間必須足夠大，而且該算法搜索機制具有較強的不確定性，特別是在初始階段，隨機搜索使得它不可避免地產生大量的局部交叉路徑、圓形路徑和鋸齒形路徑，得出的規劃曲線并不能達到預期的效果。對此，作出如下改進：

(1)改進信息素更新規則

當螞蟻利用公式(14)完成局部信息素更新后，加入全局信息素更新，在已完成搜索的路徑中，只更新最短路徑中節點的信息素，減少信息素更新時所需的時間，提高了搜索效率。全局信息素更新規則如下：

(+1)=(1-)()+Δ

(15)

(16)

式中：()表示三維環境中離散點的信息素濃度；{()}表示螞蟻(=1，2，…,)搜索的路徑長度集;為常數。

(2)改進狀態轉移規則

為提高搜索效率和算法質量，采用偽隨機狀態轉移規則。設螞蟻在時位于節點，則在+1時的位置為

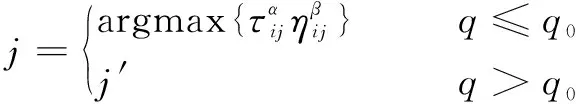
(17)

式中：為過渡比的基準速率,在(0，1)范圍內；為一個隨機數。

當<時，下一個節點直接由信息素濃度的最大值和啟發式信息的實現決定；然后，采用輪盤賭方式確定節點。具體實現過程：根據公式(17)計算出所有允許路徑的轉移概率，將轉移概率從大到小排序，用輪盤賭選擇方法確定下一個節點。

(3)改進啟發式信息函數

基本蟻群算法的啟發式信息值與下一個節點到目標點的距離呈反比，但是在不考慮當前節點和下一個節點位置的情況下，選擇的路徑不一定是最短的，在搜索后期，為加快收斂速度，應該弱化啟發式信息對路徑選擇的影響。為此，提出一種改進啟發式信息函數的方法，通過引入阻尼系數，新的啟發式信息函數如式(18)所示：

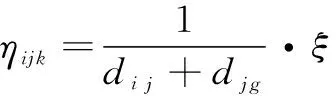
(18)

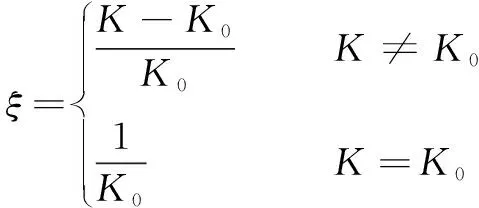
(19)

其中:為當前節點與下一節點之間的歐氏距離；為最大迭代次數；為當前迭代次數。

2.4 改進蟻群算法步驟

(1)參數初始化。初始化初始點位置、目標點位置、迭代次數、螞蟻數、信息素啟發式因子、期望啟發式因子、全局信息素更新系數和阻尼系數。

(2)開始迭代，進行路徑探索。發動螞蟻開始正向搜索，根據公式和輪盤賭法選擇下一個路徑點。

(3)局部信息素更新。當螞蟻搜尋到某一個點時，先進行局部的信息素更新，進而判斷當前螞蟻是否進入死鎖狀態。死鎖狀態時返回上一節點，更改下一節點位置；非死鎖時進入下一步驟。

(4)路徑搜索。根據偽隨機狀態轉移規則確定節點后，螞蟻持續進行搜索，最終判斷當前螞蟻是否完成路徑搜索，若當前螞蟻完成路徑搜索，則下一只螞蟻開始進行搜索。

(5)全局信息素更新。當所有螞蟻完成搜索后，需要找到該迭代過程中所有完整路徑中的最優路徑和最差路徑，并根據公式加強最優路徑上的信息素以及減弱最差路徑上的信息素。

(6)搜索結束。判斷是否滿足結束條件，如果滿足，則輸出最佳路徑；否則繼續循環執行，直到滿足結束條件或達到最大迭代次數時終止。

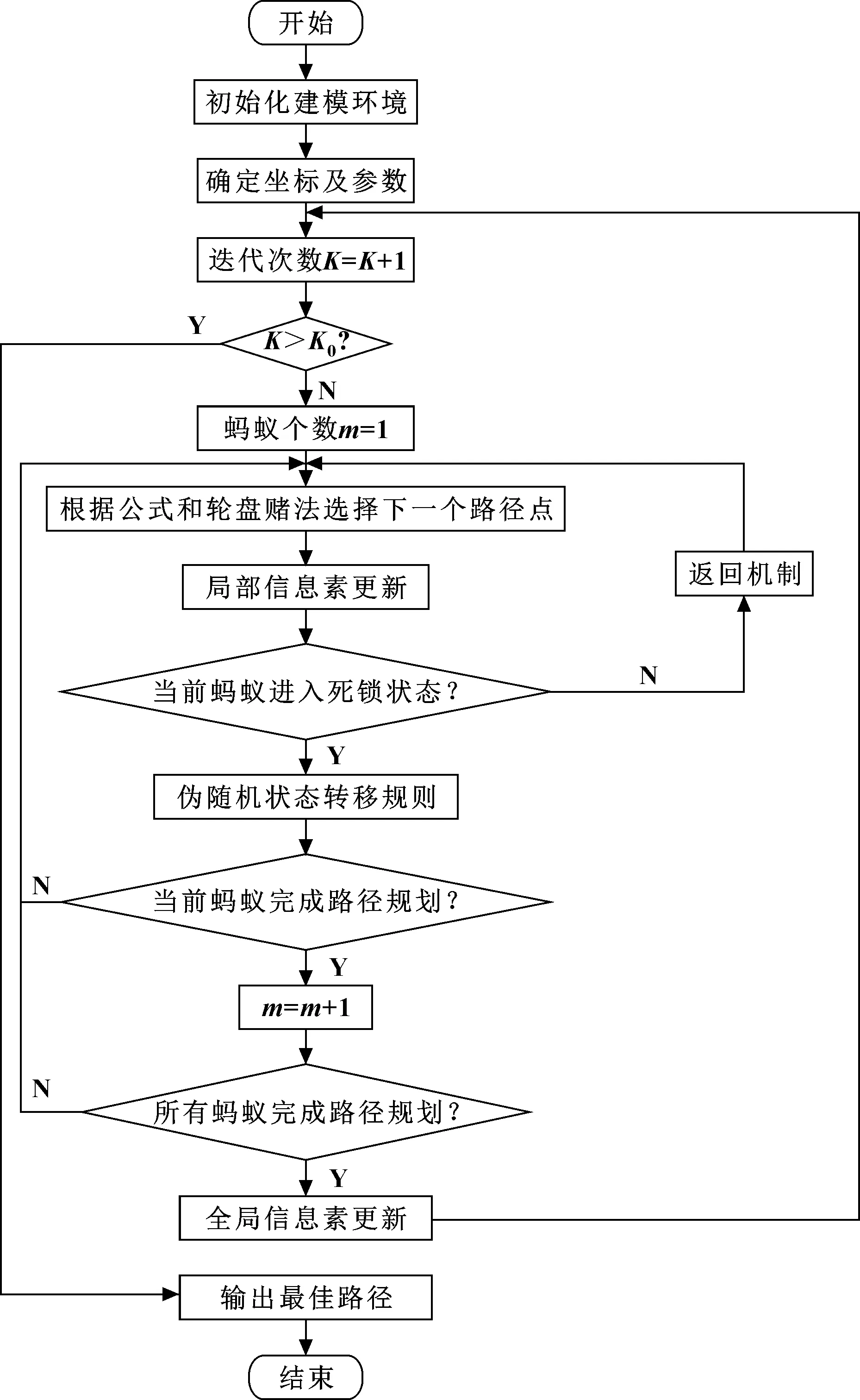
圖4 改進算法流程

3 仿真結果與分析

3.1 算法參數的選擇與分析

蟻群算法中的參數選擇對路徑規劃的效果有很大影響。仿真中采用經驗和實驗相結合的方法，通過設置不同的參數進行仿真實驗，并分析實驗結果的優缺點，選擇最佳參數組合。當螞蟻數量過多時，會削弱信息素濃度的影響。而當算法收斂速度過快時，則將削弱算法對全局搜索能力的影響。因此，在仿真實驗中，在保持其他參數不變的情況下，不斷比較和分析不同螞蟻數量得出的仿真運算結果，最終設置螞蟻數=100。

、是算法的重要參數，是信息素激勵因子，反映信息素濃度對路徑選擇的重要性，是期望的啟發式因子，反映啟發式信息對路徑的重要性。當大于時，經驗因素占主導地位，螞蟻可能重復行走路徑，進而削減搜索的隨機性；當小于時，確定性因素占主導地位，螞蟻急于綜合選擇路徑成本最小的路徑，無法實現全局最優。同樣，全局信息素更新系數和阻尼系數直接關系到全局搜索能力和算法收斂速度。在實際情況下，、、和不是獨立的，而是相互影響、綜合作用的。因此，通過嘗試各種組合模擬，并分析所得結果，最終設置參數為=1、=6、=05、=0.8。

3.2 基本蟻群算法與改進蟻群算法的比較仿真

打磨機器人通常運用于大型工件的打磨，并且在實時環境中隨時需要避開障礙物。因此,在抽象的山峰圖形中模擬機器人的環境進行仿真實驗時，采用2種蟻群算法對2組不同的初始點和目標點進行實驗，并分析仿真結果。在實驗1中設置初始點為(0 m，42 km，570 m)，目標點為(100 km，39 km，600 m)；在實驗2中設置起始點為(20 km，0 m，530 m)，目標點為(33 km，100 km，730 m)。圖5—圖8所示為基本蟻群算法和改進蟻群算法的路徑規劃水平。

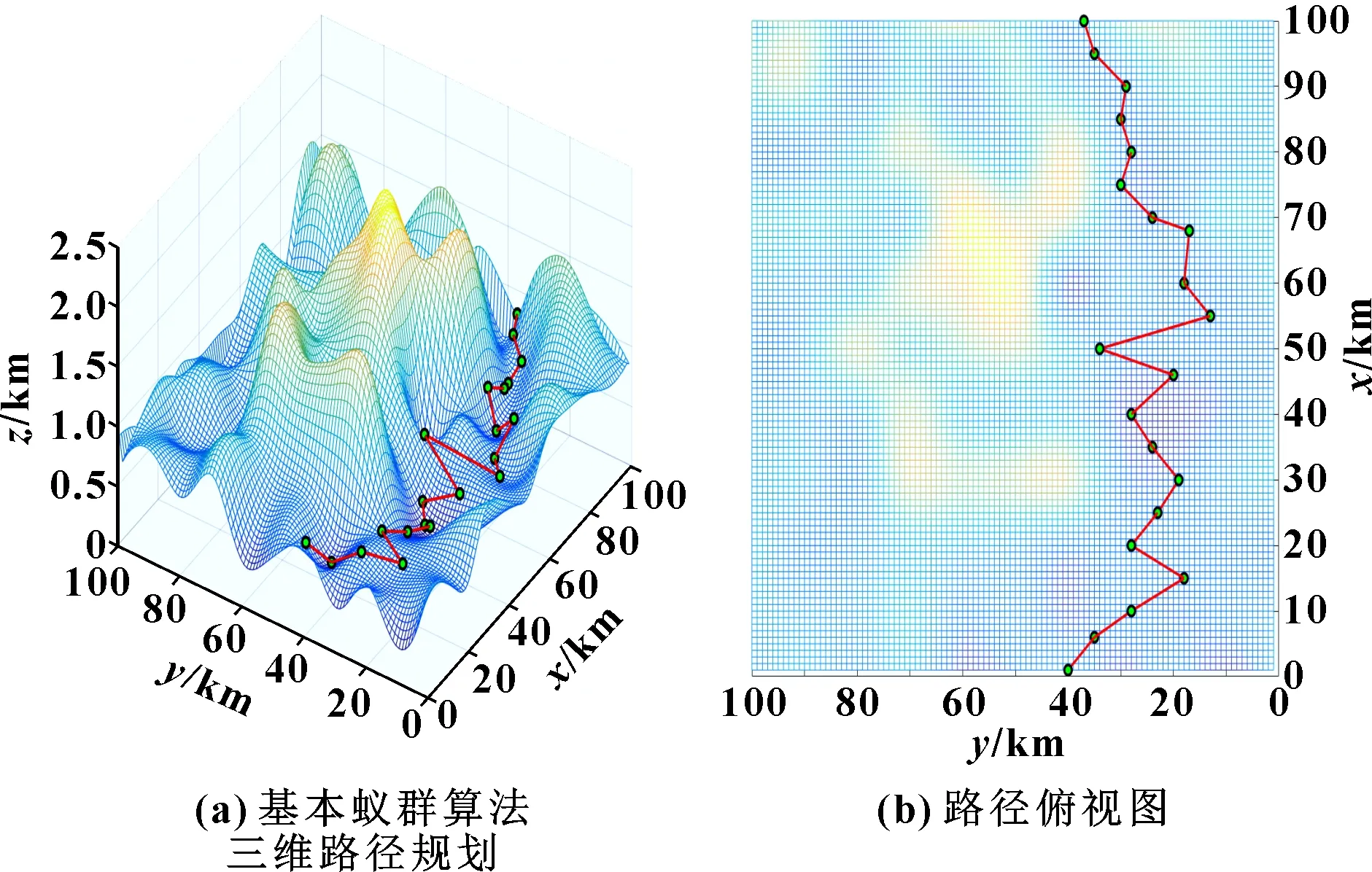
圖5 實驗1基本算法路徑

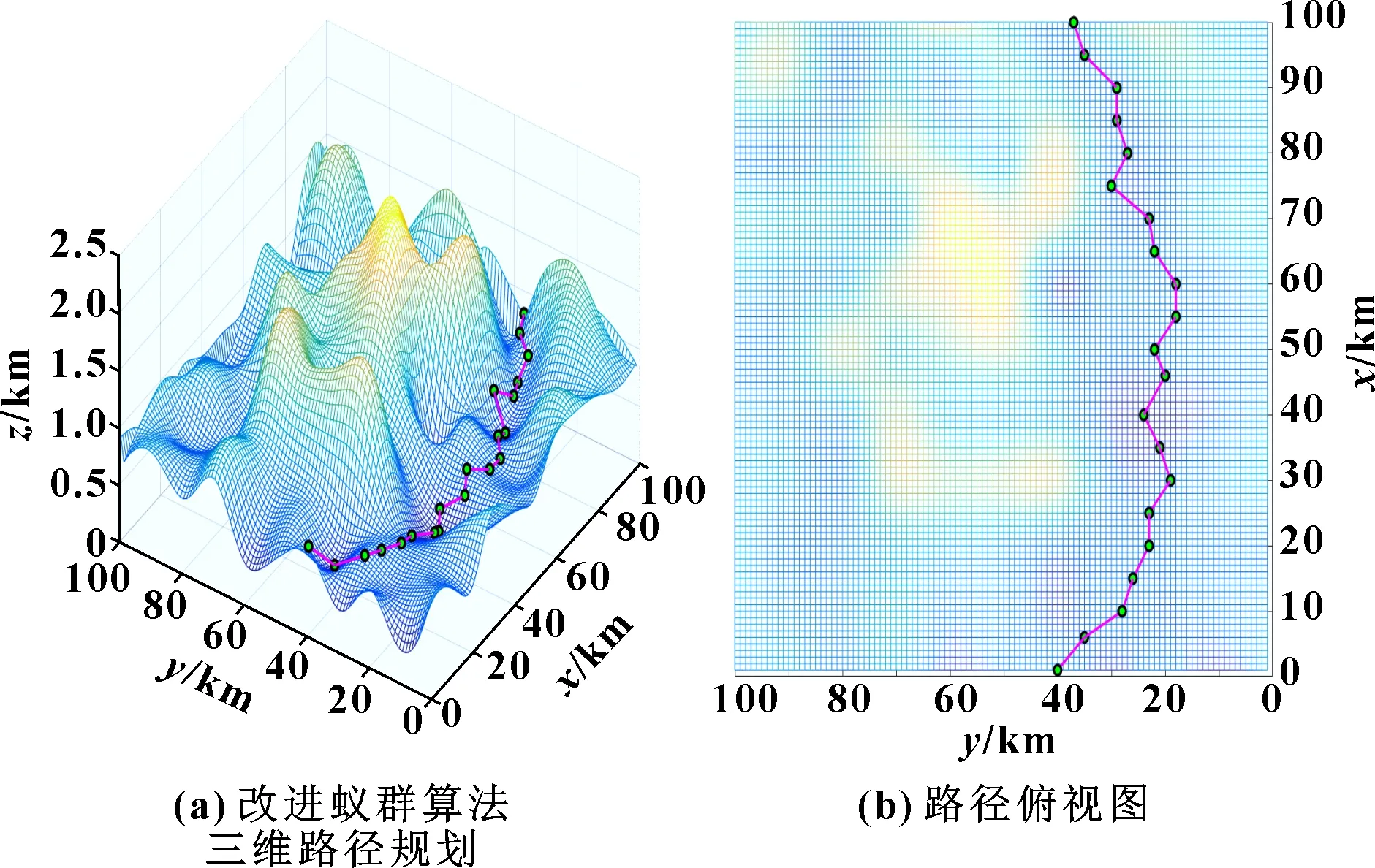
圖6 實驗1改進算法路徑

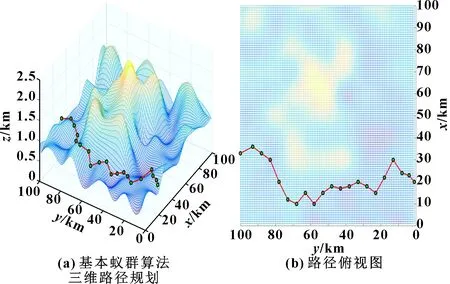
圖7 實驗2基本算法路徑

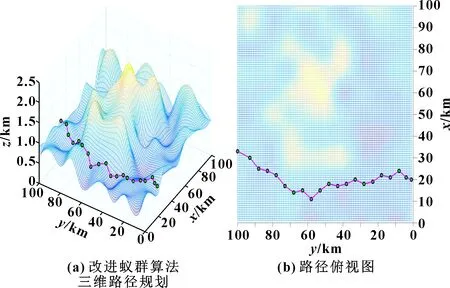
圖8 實驗2改進算法路徑

可以直觀地看到:改進的蟻群算法路徑更短，軌跡曲線更平滑。為對仿真結果作出更全面的分析，分析最佳路徑長度與迭代次數的關系，結果如圖9—圖12所示。

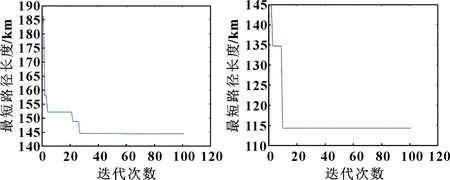
圖9 實驗1基本算法最短路徑長度變化曲線 圖10 實驗1改進算法最短路徑長度變化曲線

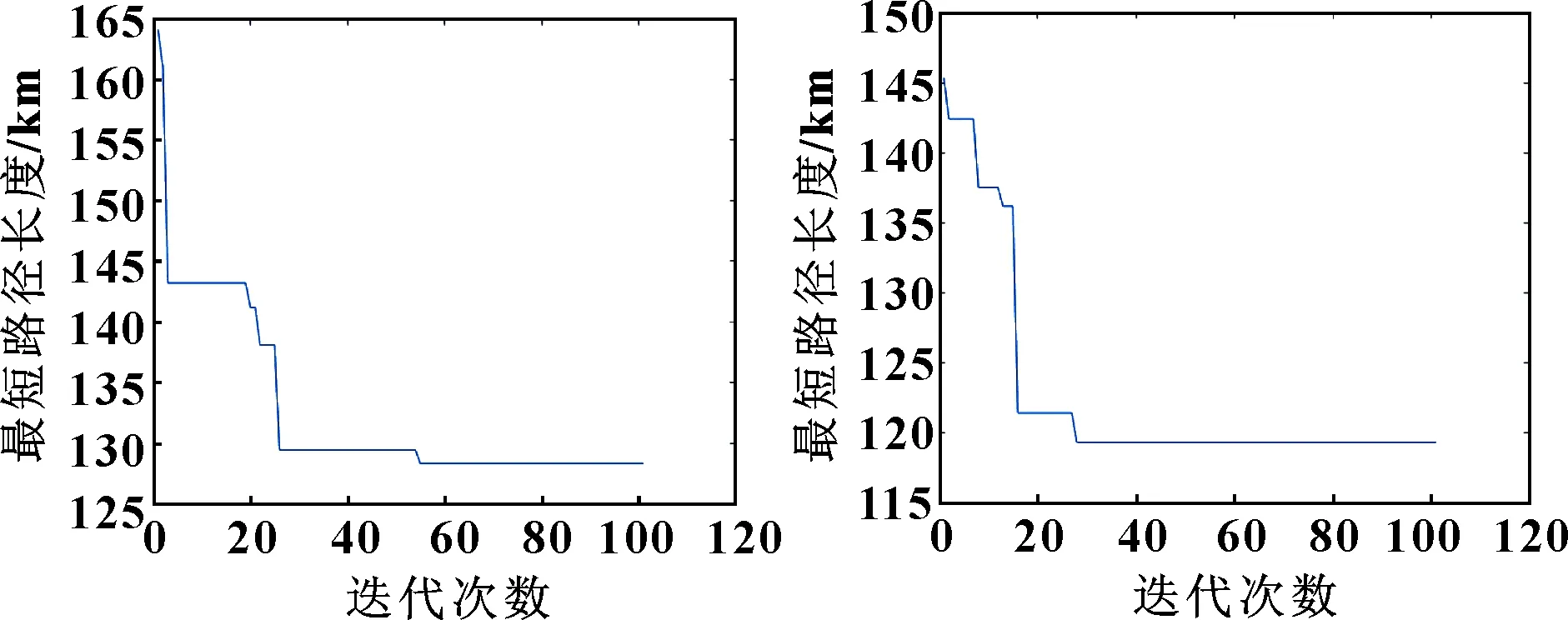
圖11 實驗2基本算法最短路徑長度變化曲線 圖12 實驗2改進算法最短路徑長度變化曲線

實驗1中,基本蟻群算法在迭代26次時得到最佳路徑長度145 km，改進蟻群算法在迭代10次時得到最佳路徑長度115 km，相比基本蟻群算法，改進蟻群算法迭代次數減少了61.5%，路徑長度減少20.7%。實驗2中，基本蟻群算法在迭代53次時得到最佳路徑長度128 km，改進蟻群算法在迭代27次時得到最佳路徑長度118 km，改進蟻群算法相比基本蟻群算法,迭代次數減少了49.1%，路徑長度減少7.8%。由上述數據可知，改進后蟻群算法的最短路徑長度平均減少了14.3%，迭代次數平均減少了55.3%。

由2組實驗結果可以看出，最佳路徑關系曲線迅速下降到某個最佳值后，迭代次數增加，最佳路徑長度不變，曲線呈水平趨勢。結果表明：改進后的蟻群算法能夠在有效避開障礙物的同時縮短迂回路徑；與此同時，搜索策略的改進有效提高了算法搜索能力。該方法可行、有效，具有重要的實際應用意義，可用于打磨機器人的路徑規劃。

4 結論

為解決打磨機器人在復雜環境下的路徑規劃存在收斂速度慢、準確性低等問題，運用改進蟻群算法進行路徑規劃。根據打磨機器人的實際結構建立了其運動學連桿模型；對其進行正逆運動學分析并驗證，改進信息素更新規則，縮短信息素更新時間，從而有效提高效率；采用偽隨機狀態轉移規則，將輪盤賭方式確定節點作為新的自適應計算方法，加快收斂速度進而弱化啟發式信息對路徑選擇的影響；通過引入阻尼系數改進啟發式信息函數。在MATLAB中進行模擬實驗，得出最佳參數組合，利用基本和改進蟻群算法進行仿真實驗，得出不同運動路徑。結果表明：與基本蟻群算法相比，利用所提出的改進蟻群算法能夠得到更短更平滑的運動路徑，最短路徑長度平均減少了14.3%，迭代次數平均減少了55.3%；結合打磨機器人刀具位置等特點，可以獲得一條路徑最短且平滑的規劃曲線，滿足打磨機器人實際應用需求。