Delta并聯機器人機構多目標優化設計

孔凡國，李肇星，柯子旭

(五邑大學智能制造學部，廣東江門 529000)

0 前言

Delta系列機器人的工業需求日益增大，使其研究與應用呈現輕量化、高速、高精度、高靈活性等趨勢。由于設計時要同時考慮的各項性能指標數量較多，基于Pareto 排序的傳統算法在處理目標數為4個或以上的問題時(即高維目標)效果并不理想，并且會產生較高的計算費用。

文獻[2]基于雅克比矩陣，對機器人運動性能的影響因素進行了研究，并分析了工作空間的主要影響因素。文獻[3]針對三自由度Delta機器人控制精度問題進行研究，詳細分析了機器人各結構誤差源對控制精度的影響。文獻[4]對三自由度 Delta 并聯機構的設計空間、空間點位置及雅克比矩陣條件數3個目標建立懲罰函數，并采用遺傳算法進行尺度綜合。文獻[5]研究了三自由度Delta并聯機構的運動學和定向能力，定向能力與尺寸參數之間的關系表明，尺寸參數不會影響奇異位置運動的輸出運動特性。文獻[6]根據工作空間、速度、加速度和慣性力的要求，建立了4個目標函數，選取NSGA-2 算法，基于iSIGHT平臺DOE方法，對3-PUU并聯機構進行了多目標優化設計，最終得到了Pareto解集。

本文作者針對運動學、動力學的多個目標，考慮機構關節的影響，選取合理的優化策略，在滿足性能要求的基礎上對機械結構進行尺度綜合，在控制計算費用的同時，使機器人具有良好的性能。

1 Delta并聯機構

以3-DOF Delta機器人為例，對如圖1(a)所示的三維模型進行抽象與簡化，建立其機構簡圖，如圖1(b)所示。將靜、動平臺簡化為2個等邊三角形，外接圓半徑分別為、。以靜平臺中心為原點建立靜坐標系-，以動平臺中心′為原點建立動坐標系′-′′′；兩坐標系軸均為豎直向上,軸指向中點,軸指向中點。

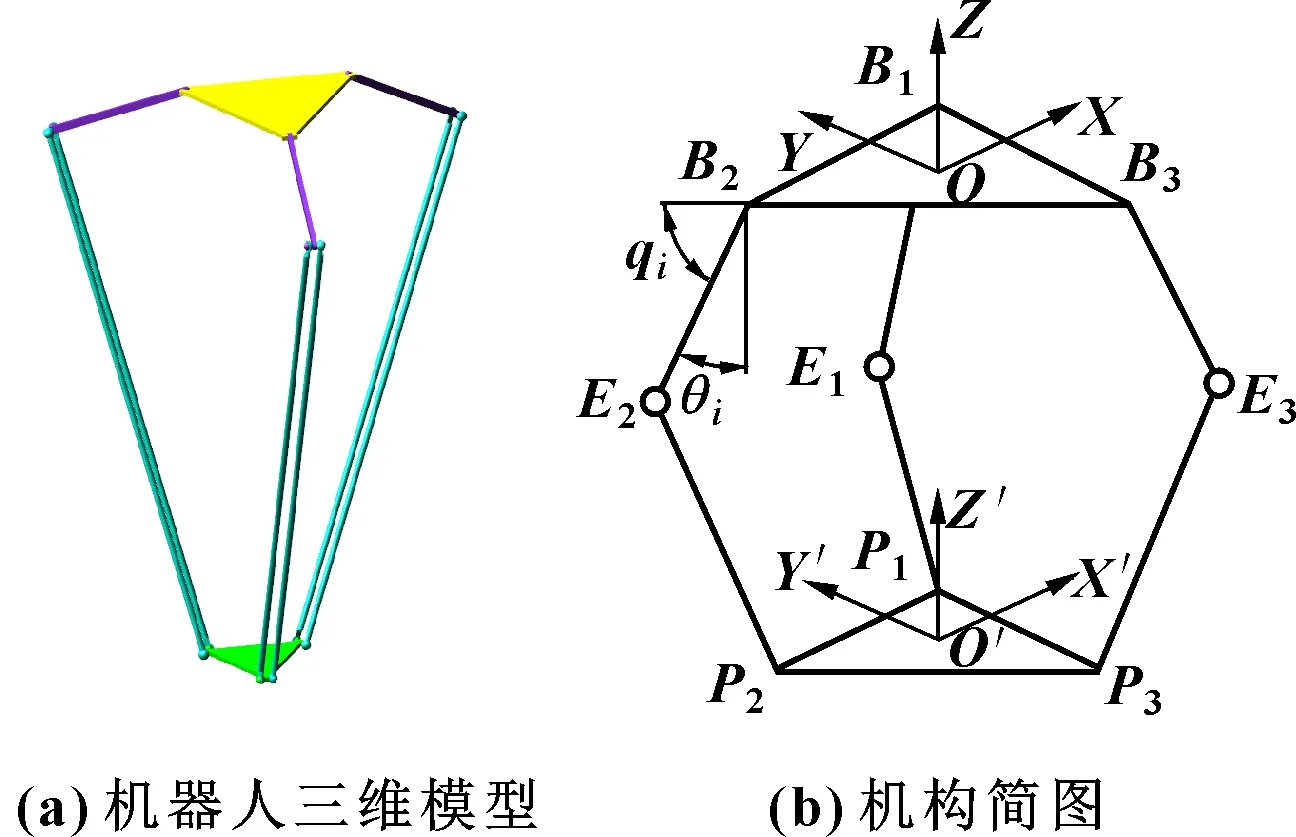
圖1 Delta機器人模型及機構簡圖

設為各主動臂長度，為各從動桿長度，為從動桿直徑,為主動臂與靜平臺軸銳角夾角，(=1,2,3)為各驅動關節的驅動角度。

2 動力學模型

計算閉鏈機構動力學模型的經典方法：考慮等效樹結構，使用Lagrange乘數或D′ Alembert原理實現運動學約束。

常用動力學建模方法包括虛功原理法、拉格朗日法、密哈爾頓原理法和牛頓-歐拉法。其中，建立牛頓動力學方程需要分析質點系的約束力，消去非獨立坐標，然后消去未知的約束力，以求得一個盡可能簡單的微分方程組。

對于并聯機構而言，動力學模型通常比較復雜不易求解，且坐標間的耦合程度會影響其運動性能和控制性能，因此需對模型進行簡化以消除桿件之間的耦合。將從動桿的質量慣量分為2份，1份分給主動臂，1份分給動平臺。將從動桿的慣量分為3份，2份分配給主動臂，1份分配給動平臺。由虛功原理可知系統受力包括動平臺受力和主動臂受力，所有非慣性力之和等于慣性力。如圖2所示，動平臺僅平動，受到自身重力和慣性力的影響；主動臂僅轉動，受到自身重力、電機轉矩和主動臂自身轉動慣量的影響。

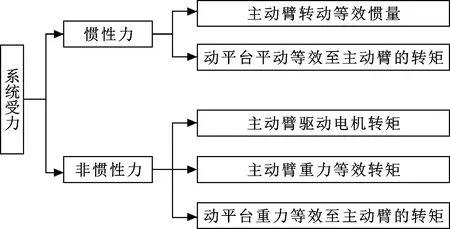
圖2 Delta機器人系統受力樹狀圖

簡化后動平臺等效平動慣量及等效慣性質量分別表示為

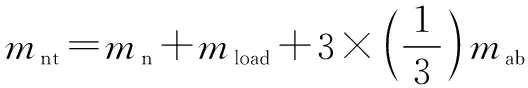
(1)

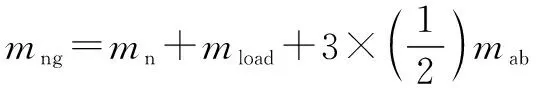
(2)

式中：為動平臺質量；為動平臺負載質量；為從動桿質量。

簡化后主動臂等效質量為

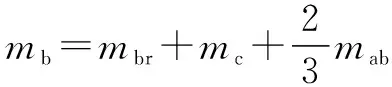
(3)

式中：為主動臂質量；為主動臂上的球鉸質量。

模型簡化后，主動臂慣性質量的質心位置為

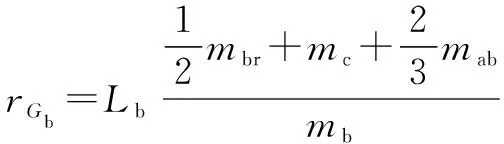
(4)

主動臂重力等效轉矩為

=···[cos]

(5)

主動臂總轉動慣量b為輸出軸轉動慣量與主動臂自身轉動慣量的和：

b=+=1，2，3

(6)

=(+)

(7)

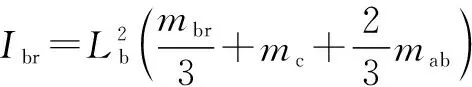
(8)

式中：為電機轉動慣量;為減速器轉動慣量;為減速器減速比。

令主動臂等效轉動慣量為

(9)

由虛功原理可得Delta并聯機構逆動力學方程為

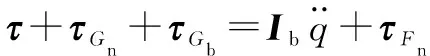
(10)

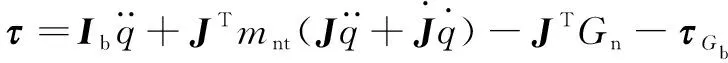
(11)

3 優化策略

對于低速并聯機構，僅考慮工作空間、雅克比條件數、奇異值等基本動力學指標即可得到較好的優化結果。上述指標可經基本代換變為單目標問題解決，優化過程較簡單。

由于機械手不停向高速度、高精度方面發展，機械手的設計優化既要滿足運動學要求，還需有良好的動態特性。對于運動構件的慣量、逆動力學方程中坐標間的耦合程度以及驅動機構運動所需的驅動力矩與驅動功率等性能指標，要建立準確的動力學方程進行優化。

考慮到機構所處的位形不同，桿件的長度、截面積不同均會影響上述指標，高速并聯機構的優化問題常常較為復雜。

本文作者以非支配排序遺傳算法NSGA-II 對Delta并聯機器人結構尺寸進行優化。優化策略：進行試驗設計，依據試驗結果規定設計變量及其取值范圍；選取試驗結果中趨勢相似的響應變量，整合后建立新的目標函數；在加以約束的情況下，借助NSGA-II完成機構運動學、動力學多目標尺度綜合。

3.1 設計變量

為研究多因子與響應變量之間的關系，進行試驗設計。選取最優拉丁超立方試驗設計方法獲得數據樣本，設置樣本為1 000組，令為局部剛度,為局部動力學靈巧度,+為驅動力矩和功率的和,為最小奇異值,為可操作度，得出自變量、、、、與響應變量的關聯度如表1所示。

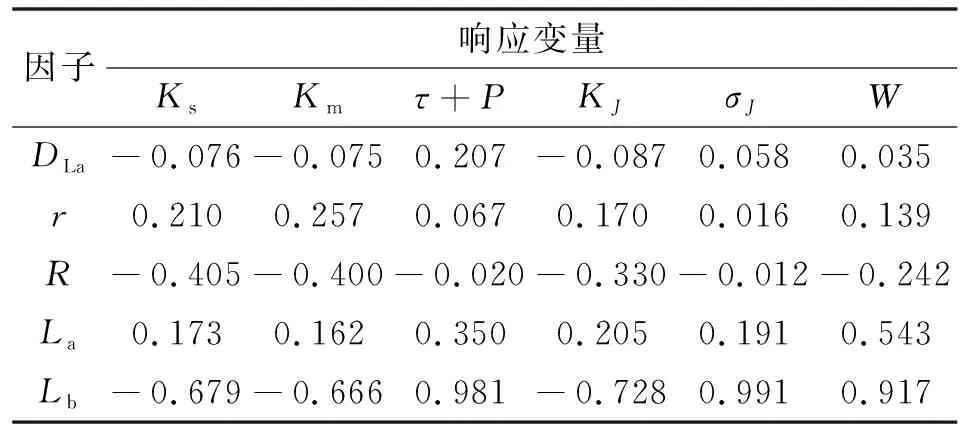
表1 因子與響應變量的關聯度

假設各桿截面形狀規則，桿質量與桿長、截面尺寸成正比關系，依據試驗結果選取動平臺半徑、靜平臺半徑、驅動臂長度、從動桿長度、從動桿直徑作為設計變量，以使機械手在給定范圍的工作空間中整體尺寸最小。

3.2 優化目標

由于具有高維目標的最優解求解時不易收斂，且可視化較差，所以本文作者將Delta并聯機構運動學、動力學的常見性能指標綜合為3個優化目標。所涉及到的指標包括：可操作度、全局剛度、全局動力學靈巧度、功率及力矩、雅克比全局條件數。

3.2.1 運動學目標

在機械手的優化設計中，由于可達工作空間的體積并不能成為評價機器人在工作空間中的整體運動學性能的唯一判據，需引入其他性能指標。對于一個并聯機構，其靈巧度可以用來反映輸入輸出運動或力之間的傳遞精度，通過求解機構速度雅克比矩陣可得出3種可影響靈巧度的指標：全局條件數指標、最小奇異值指標1/()、可操作度指標1/。將3個指標歸一化處理后求和形成綜合指標，用于評價機構全局靈巧度特性。

(1) 全域條件數指標。GOSSELIN等定義了全局指標全域條件數指標(Global Condition-number Index,GCI)評估機械手在工作區上的條件數分布，當=1時，機構處于運動學各向同性狀態。表達式為

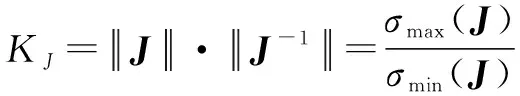
(12)

為局部條件數(Local Condition-number Index,LCI)，在可達工作空間內的均值，反映機構條件數在全域范圍內的各向同性。

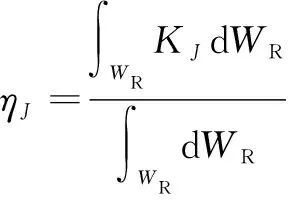
(13)

(2)最小奇異值指標。雅克比矩陣的最小奇異值()體現了輸入與輸出之間的最小傳遞放大倍數。()越大執行端對運動傳遞越快。令最小奇異值指標為1()。

(3) 可操作度指標。按YOSHIKAWA的定義，機器人雅克比矩陣與其轉置矩陣乘積的行列式值的開方體現了機構距離奇異形位和不定形位的程度，為機器人的可操作度：

(14)

當=0，機構處于奇異形位；當=∞，機構處于不定形位；當≠0且≠∞時，機構處于非奇異形位。令1/為可操作度指標。

(4)綜合靈巧度指標。先將、1()、1/進行歸一化處理；再根據該機構的各向同性和響應速度，配置權重系數，設定=0.4、=0.4、=0.2，構造綜合評價指標：

=[+()+]→min

(15)

3.2.2 動力學目標

對Delta機構的動力學逆解進行數值分析，假設動平臺運動軌跡為典型門字軌跡，對機構剛度和靈巧度進行分析。

(1)剛度指標。當外力作用在末端執行器上時，機構發生形變，形變量關系著機器人動力學性能和位置精度，尤其對于并聯機床或某些需要高精度的并聯機械手，靜態剛度(或剛度)是設計時的首要考慮因素。

在文中，僅考慮驅動機構的剛度(其他部分看作是剛體)，通過應用動態和靜態方程，得到局部剛度指標(Local Stiffness Index,LSI):

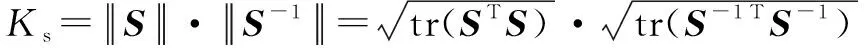
(16)

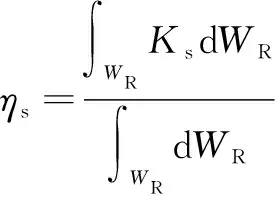
(17)

其中:為并聯機器人的剛度矩陣。為全局剛度指標(Global Stiffness Index,GSI)；由LSI在可達工作空間內的均值表示。優化時應滿足：→min。

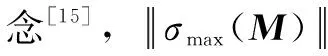
質量矩陣為

=()

(18)

設定局部動力學靈巧度指標(質量矩陣條件數)在可達工作空間內的均值，為全局動力學靈巧度指標,→min。、表達式為

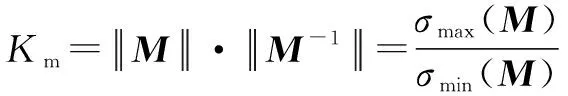
(19)

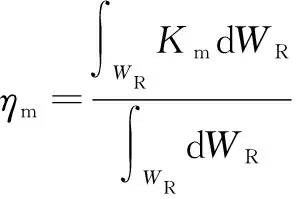
(20)

(3) 綜合動力學指標。根據DOE的結果，、趨勢相近，則令動力學目標函數為

=(+)→min

(21)

(4)控制性能指標。在執行門字形軌跡運動時，機器人驅動力矩和功率的最大值越小越好。令性能控制目標函數為

=(+)→min

(22)

3.3 約束條件

3.3.1 結構尺寸約束

Delta并聯機構的可達工作空間受到靜平臺和動平臺鉸接點分布圓半徑差、主動臂、從動桿直徑以及關節轉角范圍的約束。本文作者采用極坐標搜索法對進行取點，由圖3可知，為頂部帶有尖角的不規則幾何體。

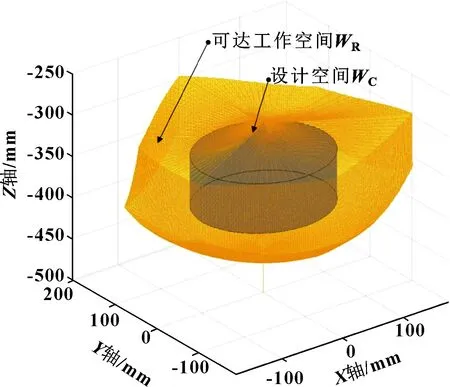
圖3 Delta機器人可達工作空間

對旋轉副轉角進行約束：

min ≤≤max =1,2,3

(23)

對球副轉角進行約束：

min≤≤max=1,2,3

(24)

連桿的干涉約束：

≥

(25)

其中：為任意相鄰兩桿間最短距離。

在實際應用中，所要求的設計工作空間一般是規則的(如長方體、圓柱體等)，文中以圓柱體為設計空間，要求設計空間包含于可達工作空間,即∈。

3.3.2 運動學約束

在可達工作空間內，給定≤5且≥0.2的約束條件，以保證機構的各向同性，提高末端動平臺的響應速度，同時避免奇異位形。

3.3.3 動力學約束

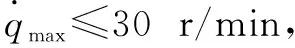
3.4 優化模型

該機構的優化數學模型可表述為

設計變量：,,,,

目標函數：

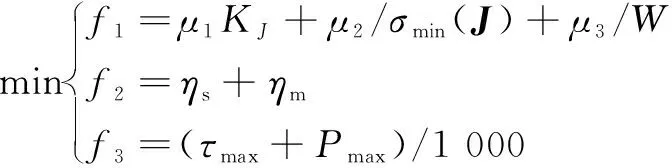
約束條件1：

約束條件2：

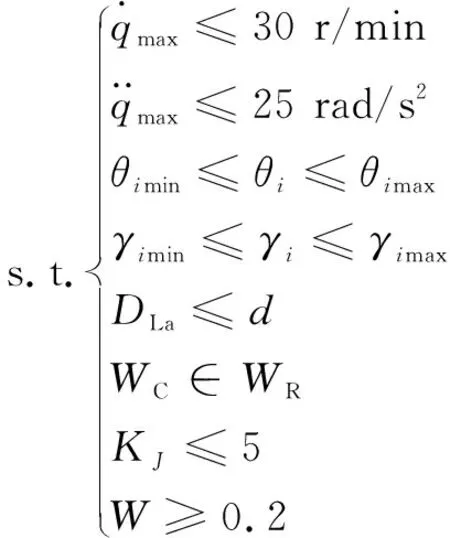
4 非支配排序遺傳算法(NSGA-Ⅱ)

4.1 多目標優化問題

NSGA-II算法多用于解決多目標問題，NSGA-II在NSGA的基礎上，增加了精英保留策略、計算擁擠距離值作為密度估計策略和快速非支配排序策略。該算法比NSGA效率更高，且不必選取參數。

4.2 算法流程

NSGA-II算法流程如圖4所示。

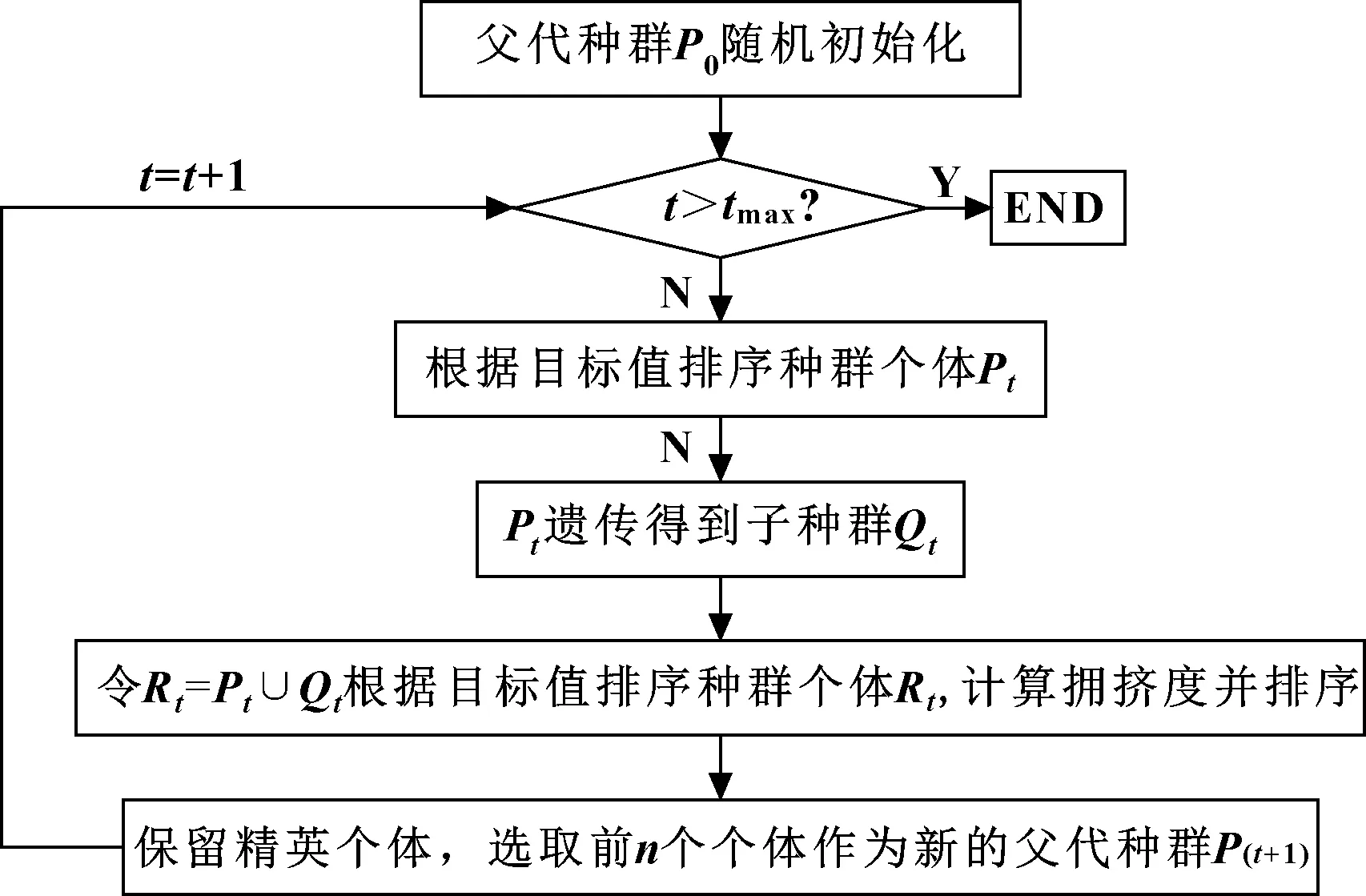
圖4 NSGA-II算法流程

5 優化結果

5.1 具體應用過程

NSGA-Ⅱ算法流程中參數設定：種群大小為24，運行代數為200代，交叉概率0.9，變異概率0.1。

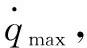
步驟4中機器人各構件均質且為剛性,運動過程中不考慮摩擦因素影響，采用5次多項式構造門運動軌跡函數如圖5所示。圖中，起點(-100,0,-380)、中間點(-100,0,-330)、中間點(100,0,-330)、終點(100,0,-380)。

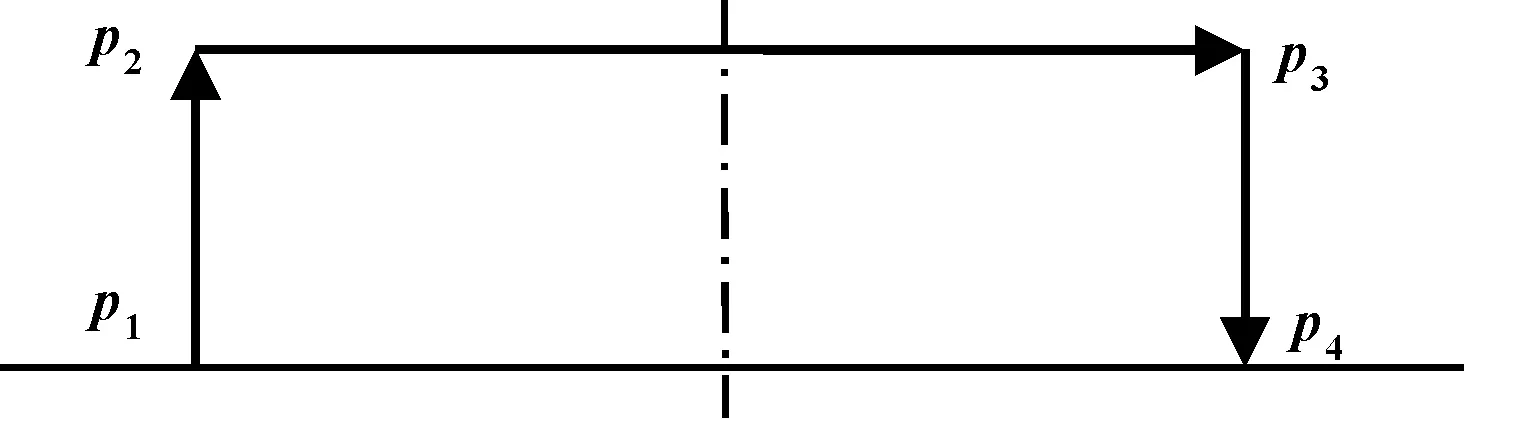
圖5 末端動平臺的運動軌跡

5.2 運算結果

通過iSIGHT軟件迭代計算后得到Pareto前沿解，如圖6所示。如表2所示，選取其中各項目標值較優的8組解，其中第0組為初始值作為參考；第1組為軟件給出的最優解。

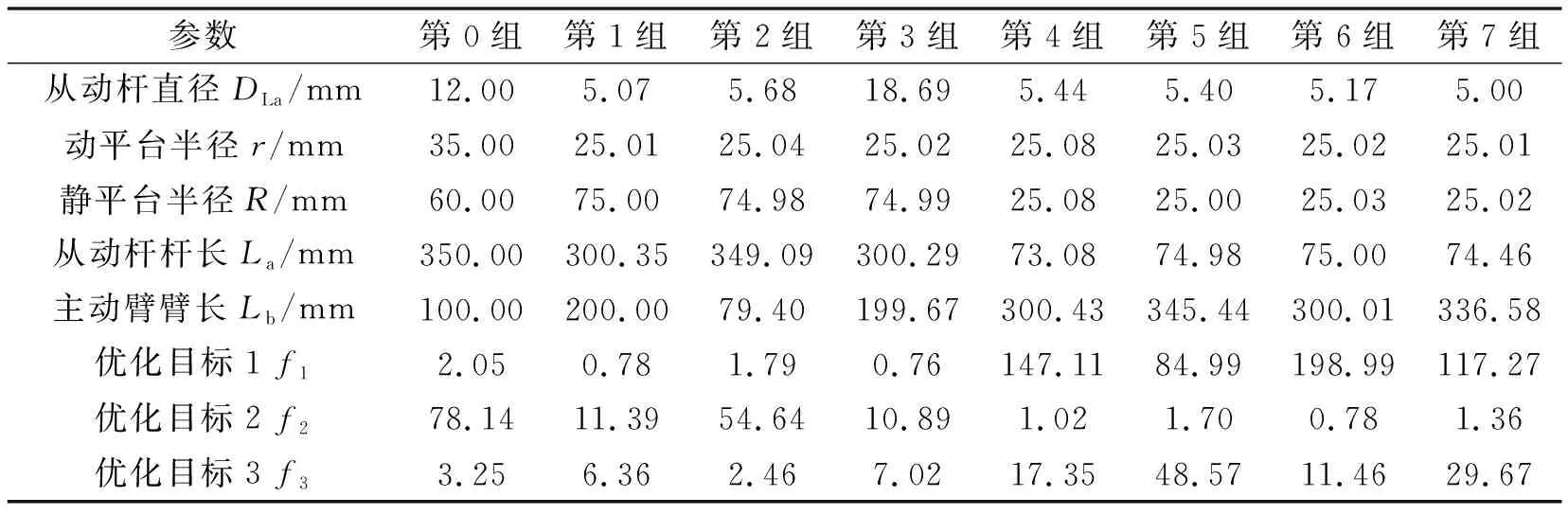
表2 多目標優化結果

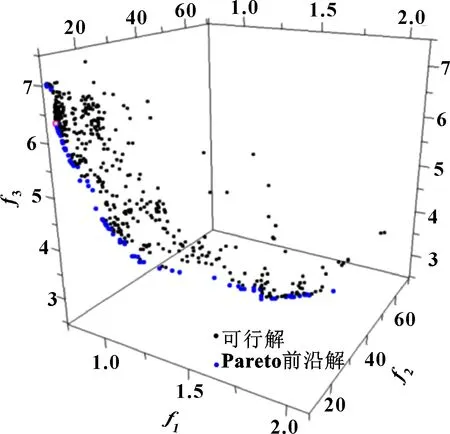
圖6 Pareto 最優解

為驗證優化策略的可行性，設計不同維度的目標函數,對比的優化解集，對比方案中僅將拆分為2個單獨目標=、=。結果表明：在使用同種算法、相同迭代次數下，方案1(3個目標函數)生成可行解624個、最優解13個，方案2(4個目標函數)生成可行解62個、最優解1個。

6 結論

本文作者通過DOE選定設計變量并建立目標函數，利用控制關鍵變量控制整體優化過程；通過整合趨勢相近的目標，將目標數降為3個，相對于更高維度的目標數，文中的優化策略收斂性好，可視化程度強，計算費用大大降低，驗證了優化策略的合理性。Pareto前沿圖表明NSGA-Ⅱ算法在此次設計優化過程中，在保證機構滿足設計空間和特定軌跡的條件下，能保持良好的綜合性能，減小了整體尺寸，體現了優化策略的有效性。給出了部分Pareto前沿解供設計人員參考，后續還可加入模態分析、誤差分析等使優化策略更加完善。