石材雕刻機械臂運動學性能的分析與優化

尹方辰，史宏偉，紀清智，陳寅昊，王柴志，黃國欽，崔長彩

(華僑大學制造工程研究院，福建廈門 361021)

0 前言

在石材產業中，石雕作為一門藝術，是石材與雕刻藝術的完美結合，一直記錄著世界文明的發展歷程，是人類文化及藝術傳承的主要載體之一，具有較高的藝術價值和文化價值。立體石雕更是以其整體形狀與輪廓構造復雜、曲面繁多等特點成為附加經濟值較高的石材制品。在立體石雕產業中，加工是產業核心，立體石雕加工是離散制造形態，無法像鞋帽服裝一樣流水化生產，不能通過擴充設備數量、提高工人數量來降低單價成本，且產品的質量完全取決于專業工人的技術積累，因此新技術的引入是行業命脈。近年來，以機械臂為代表的智能加工裝備，可以最大限度地代替人工勞動，降低人力成本，同時可以在各種復雜的環境中完成加工作業，在工件尺寸、加工效率與造型靈活性等方面已經表現出傳統石材數控雕刻中心無法比擬的優勢。在國內，廈門大學、山東大學與華僑大學等單位相繼投入力量研發石材雕刻機械臂，在機械臂雕刻系統的總體設計、雕刻刀位軌跡生成與雕刻過程的仿真上取得了大量的研究成果。在國際上，ANDERSSON和JOHANSSON研究了機械臂雕刻過程中的力控方法，從而保證了機械臂雕刻過程的穩定性；HU和CHEN提出了一種機械臂雕刻復雜曲面的軌跡優化方法，為機械臂雕刻復雜曲面的軌跡設計提供了新的思路。

石材雕刻機械臂是六自由度串聯機構，在其工作空間內運動性能的變化相當復雜，且立體石雕的工件毛坯尺寸通常較大，雕刻機械臂通常在較大的工作空間內進行加工，因而石材雕刻機械臂在其可達工作空間內運動性能的優劣直接影響立體石雕產品的加工質量。本文作者針對這一問題，對石材雕刻機械臂的運動性能進行分析與優化，并給出其最優工作空間的選取方法。為分析石材雕刻機械臂的運動性能，需要建立能描述石材雕刻機械臂運動性能的指標。機械臂雅克比速度矩陣具有奇異性，其求解逆矩陣精度較低，只可以定性地描述石材雕刻機械臂的運動性能。然而，石材雕刻機械臂的工作空間不僅要避開奇異區域，而且由于雕刻實際操作和控制精度的要求，工作空間應該盡量遠離奇異區域。靈巧度是定量描述石材雕刻機械臂運動性能優劣的一個有效指標，它是指機器人沿任意方向運動并施加力和力矩的能力的難易程度。靈巧度越高，機械臂執行器末端越遠離奇異點，可加工范圍和控制精度都能顯著提高，該指標在研究機械臂的連桿尺寸設計、軌跡規劃和避障等問題時具有重要的指導作用。國內外許多研究機構對機械臂本體和機械臂加工系統進行了靈巧度分析及其加工空間優化。王偉和贠超優化了磨削機接觸輪相對于機械臂基坐標系的位移偏移量，獲得了機械臂砂帶磨削系統具有最高靈巧度的磨削工作空間。郭肖鵬和張志利建立了排爆機械臂在工作空間內的靈巧度優化目標函數，并通過遺傳算法對目標函數進行求解，實現了排爆機械臂靈巧度的優化。菅奕穎以工作空間與靈巧度為約束條件,對不同構形的六軸工業機械臂進行構形優化設計,對相同構形的機器人進行尺寸參數優化設計。肖華等人對一種六自由度壓力容器檢測機械臂的靈巧度進行仿真分析，并給出指定操作點的機械臂靈巧度仿真結果。對于石材的機械臂雕刻加工而言，如果石材工件毛坯能夠擺放在合理的位置上，使得機械臂能夠運動在其靈巧度最優的工作空間內，機械臂的運動性能與加工精度將得到顯著提高。

本文作者基于D-H方法建立石材雕刻機械臂的運動學模型；提出一種適用于石材雕刻機械臂的靈巧度指標，并推導出它在工作空間內任意一點的計算方法；通過對石材雕刻機械臂加工軌跡進行仿真，分析機械臂在關節空間和操作空間坐標下靈巧度的變化規律。采用Dijkstra優化理論，以靈巧度最大為目標函數，在石材雕刻機械臂可達工作空間內，尋優得到其最優工作空間，并采用ADAMS仿真軟件驗證優化結果的有效性。

1 石材雕刻機械臂的運動學建模

1.1 D-H參數建模

本文作者所研究的石材雕刻機械臂如圖1所示，其主體部分由德國庫卡(KUKA)公司所生產的KR240-R2900高精度機械臂與意大利HSD公司生產的高速電主軸(30 kW,12 000 r/min)構成,并配備專用的石材雕刻刀具。由于石材雕刻機械臂中所有關節軸都是旋轉副，使用D-H參數建立KR240-R2900機器人每個連桿的坐標系，如圖2所示。此外，末端執行器的裝載也會影響機械臂的運動學性能，為標定末端執行器參數與機械臂的負載參數，在圖2中建立虛擬關節坐標系{}與腕關節坐標系{6}相連。根據圖1所示的石材雕刻機械臂機械結構參數，確定石材雕刻機械臂各連桿D-H參數如表1所示。

圖1 石材雕刻機械臂結構

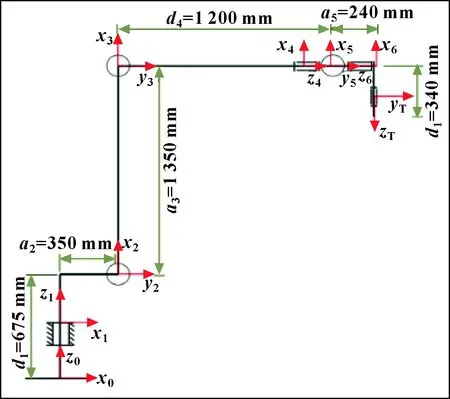
圖2 石材雕刻機械臂D-H參數坐標系

表1 石材雕刻機械臂D-H參數

-1、-1、和為連桿參數。其中，連桿長度是沿-1方向從-1軸到軸的距離；連桿扭角-1是繞-1軸從-1軸旋轉到軸的轉角；關節距離是沿方向從-1軸到軸的距離；關節轉角是繞軸從-1軸旋轉到軸的轉角。

1.2 石材雕刻機械臂的正逆運動學建模

根據圖2與表1,將所有的齊次變化矩陣相乘可得到石材雕刻機械臂末端位姿的變換矩陣。齊次變換矩陣已由D-H參數給出，因此正運動學方程可表示為

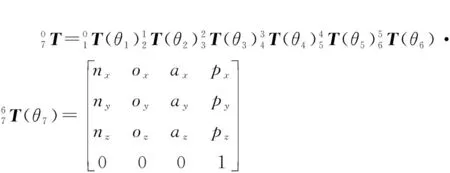
(1)

式中:[ ]表示變換矩陣中坐標系相對于軸的旋轉向量，同理[ ]、[ ]分別表示變換矩陣中坐標系相對于、軸的旋轉向量；[ ]表示機械臂末端刀具的位置向量。

根據每個坐標系的建立步驟，可將相鄰坐標系變化的表達式描述為

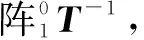
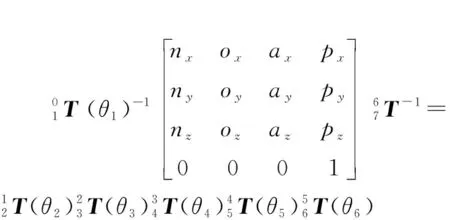
(2)

從等式(2)可以推導出下式：

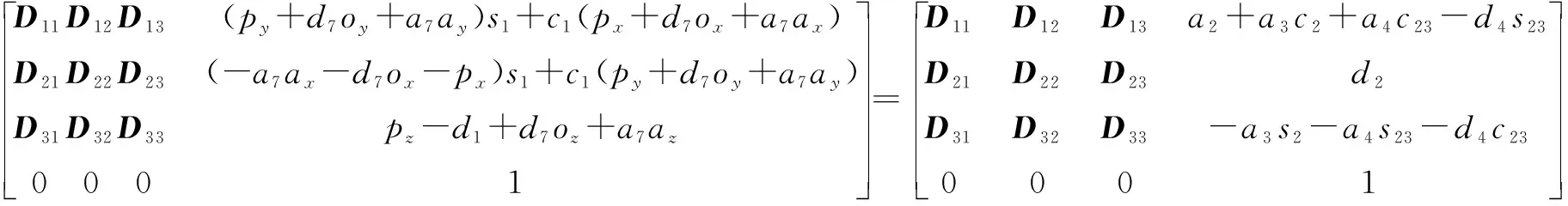
(3)

式中：為sin(+)；為cos(+);—為石材雕刻機械臂末端刀具姿態的矩陣。

令等式(3)左右兩側矩陣第二行第四列元素相等，得等式(4)如下：

(---)+(++)=

(4)

由等式(4)可得，關節角的逆運動學方程如下：

=arctan(++,++)-

arctan[,(-1)·

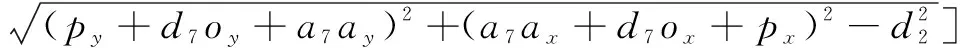
(5)

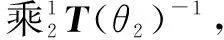
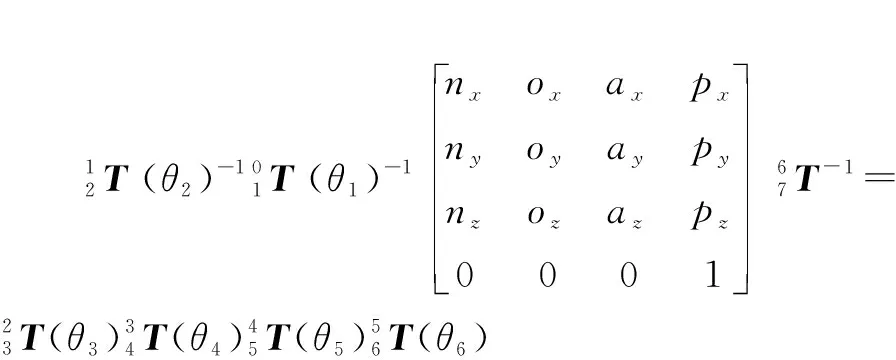
(6)

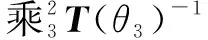
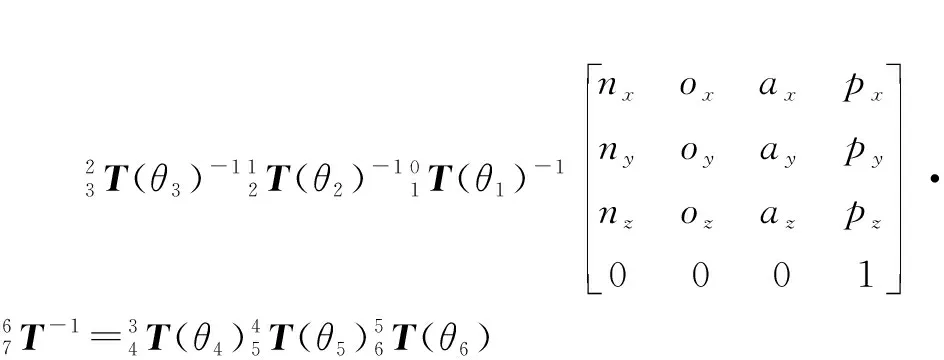
(7)

在等式(7)中只有3個未知量，因此求解等式(7)便可得到剩余的3個關節角、和的逆運動學方程。由建立的逆運動學方程可知，求解得到的石雕機械臂姿態解不是單一解而可能存在多個解。這表明當石材雕刻機械臂的末端執行器到達加工空間中的任意位置時，會存在不同的加工姿態。因此，石材雕刻機械臂能以不同的姿態到達同一個加工位置，并且其在不同的姿態下的運動性能也不相同。因此在實際的石材雕刻加工中，機械臂需要以具有最優運動性能的姿態來雕刻石材，以保證加工質量。

2 石材雕刻機械臂的靈巧度

在機械臂運動學中，機械臂雅克比矩陣反映了操作空間機械臂末端速度與關節空間的關節角速度之間的關系，如式(8)所示：

=()d

(8)

式中:()表示機器人的雅克比矩陣；表示末端執行器的速度。

對于文中所研究的石材雕刻機械臂，其雅克比矩陣為6×6階方陣，當存在一組關節角度，使得雅克比矩陣行列式為0，此時機械臂有一個或者多個關節的軸線重合，機械臂就會喪失一到多個自由度。此時，末端執行器的坐標稱為奇異點，奇異點的速度反解不存在，機械臂不具有可操作性，并且其運動性能指標都會變差。因此，在選擇機械臂加工位姿時，應盡量遠離奇異點。

機械臂的運動學性能指標是一個標量，用于衡量機械臂沿任意方向運動并施加力和力矩的能力。雅克比矩陣的條件數()的倒數可以作為運動性能指標來衡量機械臂末端執行器距離奇異點的距離，它被稱為機械臂的靈巧度。其中，石材雕刻機械臂的雅克比矩陣條件數()可表示為

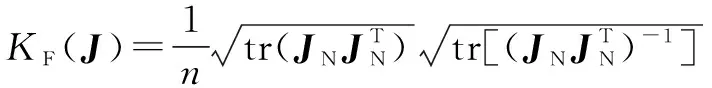
(9)

其中:tr()表示雅克比矩陣的跡；表示雅克比矩陣的維數。

則石材雕刻機械臂的靈巧度可表示為

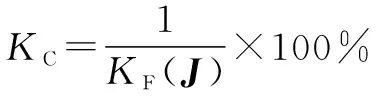
(10)

對于石材雕刻機械臂，為7。需要注意的是，這里的不是公式(8)中的雅克比矩陣()，而是雅克比矩陣的規范標準型。 規范標準類型的引入是為了解決雅克比矩陣的內部單位不一致的問題，其定義為

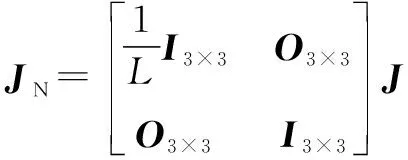
(11)

其中:、、分別是3×3的單位矩陣、3×3的零矩陣和雅克比矩陣。

特征長度的定義：確保雅克比矩陣的所有元素都有相同物理單位的歸一化長度，計算公式為

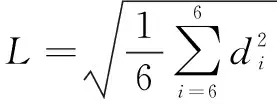
(12)

當條件數()為最小值時，石材雕刻機械臂的特征長度為一個關節點的轉軸與末端點的轉軸之間距離的均方根值。為獲得石材雕刻機械臂的特征長度，建立目標函數如下：

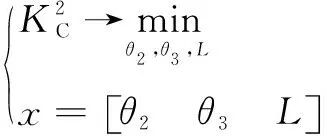
(13)

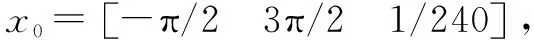
=-1.314 rad= 2.127 rad= 233.14 mm

根據公式(10)與式(11)可知，0<()≤1。當()=1時，雅克比矩陣的所有奇異值都相等，其對應的石雕機械臂運動性能最好。相反，當()趨于0時，雅克比矩陣的最小奇異值趨于零或者最大奇異值趨于無窮大。此時，末端執行器接近奇異點，其對應的石雕機械臂運動性能會顯著降低。因此，為使石雕機械臂具有良好的運動性能，理論上應盡可能選擇在()值大的區域運動。

3 石材雕刻機械臂運動性能分析

在使用石材雕刻機械臂進行雕刻加工時，常用走刀軌跡有回字形軌跡和工字型軌跡兩種。文中以回字形走刀軌跡為例，在雕刻機械臂的可達工作空間內，對其進行運動學性能分析。在石材雕刻機械臂加工路徑的離線仿真中，設定末端刀具姿態垂直于工件表面，在機器人末端刀具的姿態(，，，，，)中，只有、兩個方向會隨著加工路徑而發生變化,如圖3所示。將機器人操作空間坐標系的原點定義為，當石材雕刻機械臂在-平面上以不同的高度進行加工時，根據上文所提出的靈巧度指標()，可以獲得石材雕刻機械臂在其可達工作空間內的運動學性能的分布。

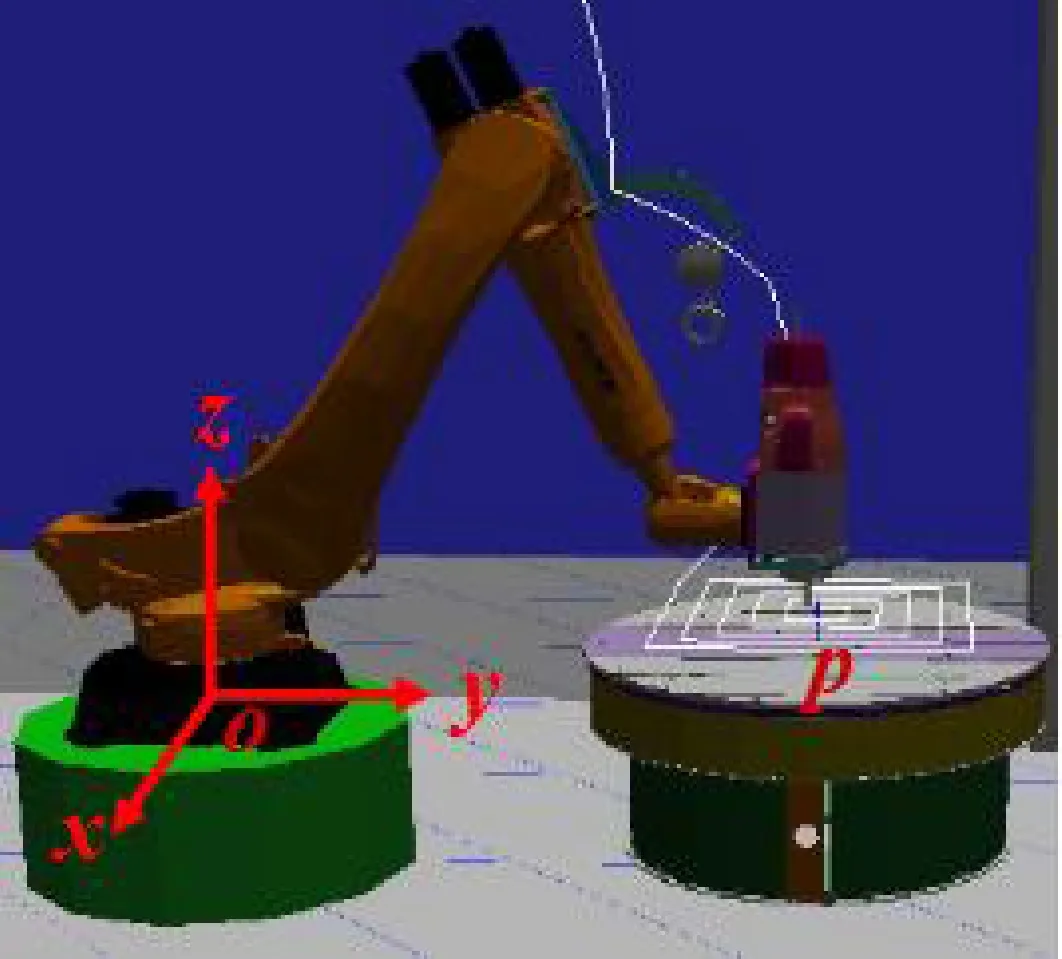
圖3 石材雕刻機械臂加工空間區域示意

3.1 關節空間下的運動性能分析

如圖3所示，工作臺中心的坐標為(0,2 000,0)，軸的加工范圍為-500～500 mm，軸的加工范圍為1 500～2 500 mm。將軌跡位移每100 mm定義為一個單位步距，在石雕機械臂走回字形軌跡的過程中，軌跡的步數與-平面軌跡之間存在如下關系：

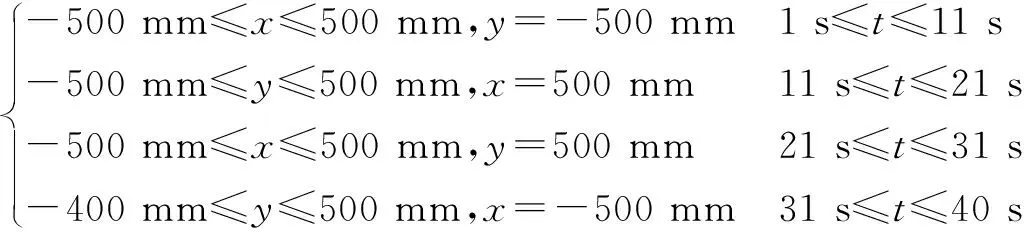
(14)

在石雕機械臂走回字形軌跡過程中，、和軸僅有微小變化，而機械臂軸不影響其加工性能，和軸主要影響機械臂末端位置的變化。因此,為分析石雕機械臂在其關節空間下的運動學性能，設定、、和為常數，通過改變和來分析石雕機械臂在關節空間內運動學性能的變化規律。變量條件設置如下：

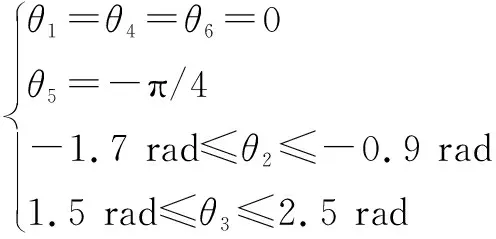
(15)

石雕機械臂在操作空間內和軸可達角度范圍分別為[-1.7 rad,-0.9 rad]和[1.5 rad,2.5 rad]。在關節空間內計算得出石雕機械臂運動學性能隨和軸角度變化分布，如圖4(a)所示。在第1.1節機械臂D-H參數建模中提到，機械臂末端執行器的質量也會影響其運動學性能。因此，本文作者以相同的角度約束條件分析石雕機械臂在未裝載末端執行器情況下的關節空間運動性能分布情況，結果如圖4(b)所示，與裝載電主軸情況下的機械臂運動性能進行比較。

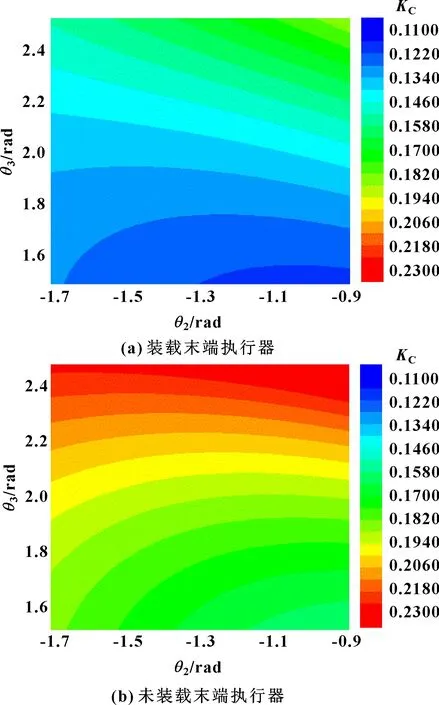
圖4 石雕機械臂在關節空間下的運動性能圖譜

由圖4可知：石雕機械臂未裝載末端執行器時靈巧度指標在0.16～0.24范圍內分布，裝載末端執行器時靈巧度指標在0.12～0.19范圍內分布，兩者具有類似的變化趨勢。末端執行器的裝載降低了機械臂的靈巧性能，石雕機械臂整體運動性能下降。同時，石雕機械臂在其工作空間內，其運動性能隨著和的增大逐漸增強。因此，在末端軌跡點不變的條件下，石雕機械臂應該選擇和角度較大的姿態進行加工。

3.2 操作空間下的運動性能分析

石雕機械臂在實際雕刻加工中，逐層向下走回字形軌跡，在操作空間中可視為在不同方向高度上進行加工。為研究石雕機械臂在操作空間下運動性能分布，將-平面中的工作區域按每100 mm分成11×11=121個步數點,計算出石雕機械臂在不同高度下，每個步數點位置下的靈巧度指標()，擬合得出靈巧度的等高線，即運動性能圖譜，如圖5所示。

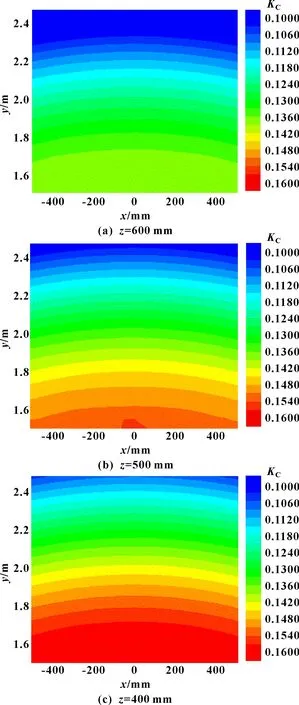
圖5 不同高度z下的x-y截面運動性能圖譜

由圖5可以看出:在方向不同高度上，石材雕刻機械臂的運動性能分布均關于軸對稱。這是由于石雕機械臂軸的變化不會影響機械臂的運動性能，且靈巧度指標是以同心圓形狀向外擴散，而不是以平行線形式遞減，同樣驗證了第3.1節中所述的軸不會影響機械臂的運動性能的假設。同時，在相同的方向高度上，隨著方向的位移不斷增加，即機械臂不斷向外延伸加工，其運動性能逐漸降低。當加工高度為600 mm時，石雕機械臂在-截面上靈巧度分布范圍為0.087～0.139，在=500 mm和=400 mm高度下靈巧度分布范圍分別為0.096～0.156、0.104～0.162。可以發現，隨著雕刻過程的進行，即末端執行器垂直工件表面向下運動時，石雕機械臂在不同高度下時，-截面的整體運動性能也隨之逐漸增強。

進一步地，選取二維空間平面-，其中軸范圍是-500～500 mm，軸范圍是100～1 100 mm，方向選取1 500、2 000、2 500 mm 3個位置，以同樣的加工姿態，分析在方向不同位置上-截面石雕機械臂運動性能分布情況，如圖6所示。

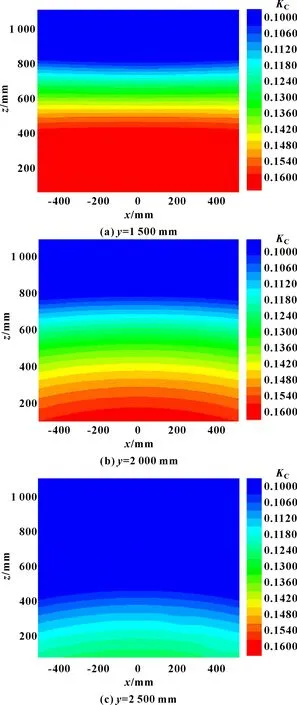
圖6 y方向不同位置處x-z截面運動性能圖譜

由圖6可知：在方向不同位置處，石雕機械臂的運動性能均隨著高度的減小而增強；當=1 500 mm時，機器人在-截面上靈巧度分布范圍為0.076～0.175；當=2 000 mm和=2 500 mm時，-截面上石雕機械臂靈巧度分布范圍分別為0.053～0.160、0.027～0.126。可以發現，隨著石雕機械臂向外伸展加工，它在方向不同位置處-截面的整體運動性能隨之逐漸減弱。

4 基于Dijkstra優化理論的石雕機械臂工作空間優化

一般石雕工件毛坯多為規則幾何體形狀，而毛坯位置的擺放大多遵循人為經驗選擇，對毛坯工件的擺放尚未有理論的指導依據。根據前文的分析可知，石雕機械臂在不同的關節空間與操作空間下，其運動性能有很大差別。因此，需要對石雕機械臂的固有靈活工作空間進行優化，使得機械臂的作業對象完全布局在該優化空間內，這樣石雕機械臂在進行雕刻加工時，才會具有更好的運動性能。文中所研究的石材雕刻機械臂的可達工作空間為工作臺中心上方1 000 mm×1 000 mm×1 000 mm的立方體空間區域。石材雕刻機械臂在其可達工作空間中的靈巧度分布如圖7所示。其中，預設的工件毛坯尺寸為500 mm×500 mm×500 mm，以其靈巧度最大的加工區域為優化目標進行優化。

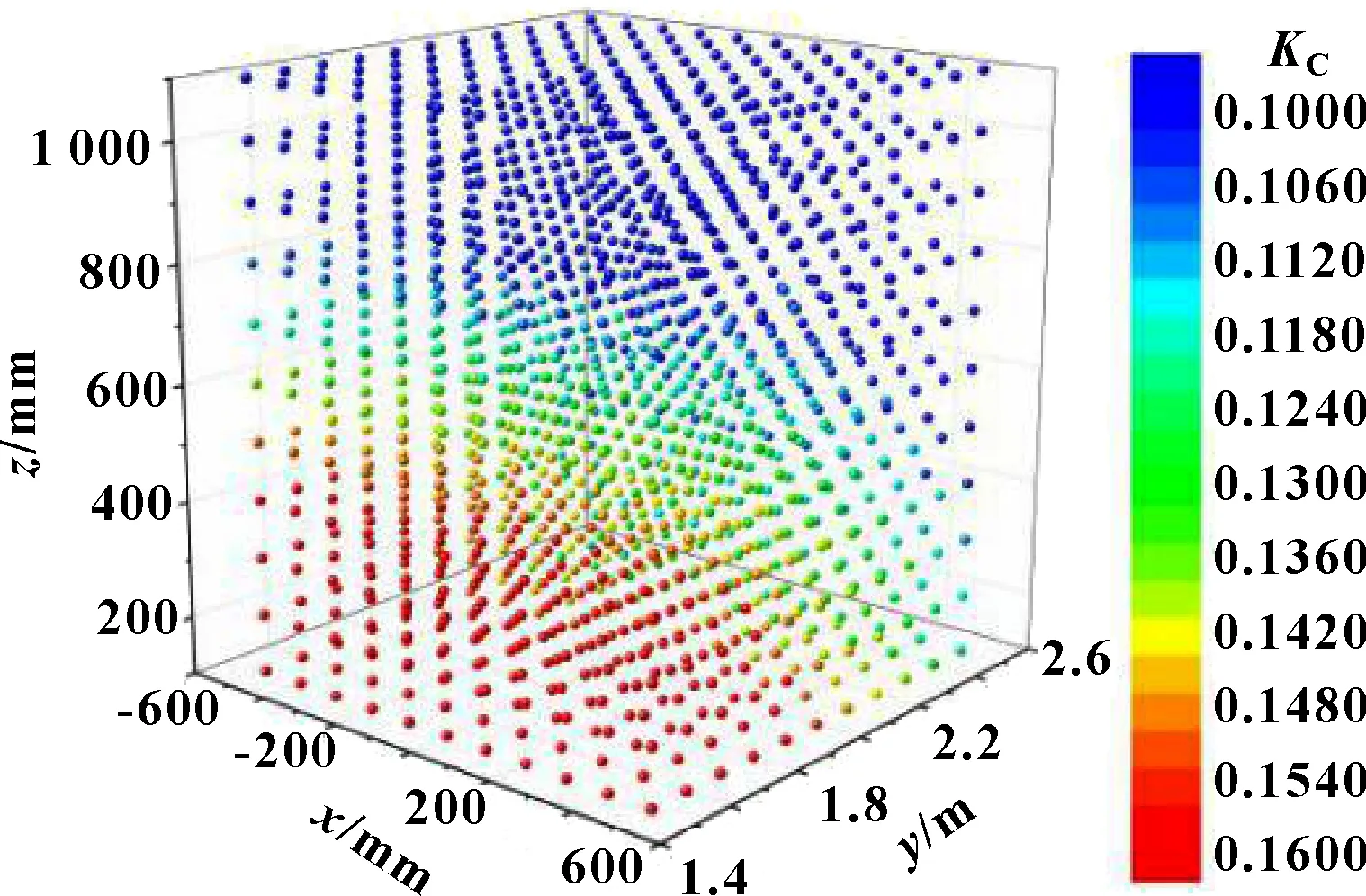
圖7 石材雕刻機械臂在工作空間下的運動性能圖

4.1 基于Dijkstra理論的優化過程

Dijkstra優化理論是典型的單源最短路徑算法，用于計算一個節點到其他所有節點的最短路徑，其主要特點是以起始點為中心向外逐層擴展，直到擴展到終點為止，其搜索優化過程如圖8所示。在圖8中，通過建立的二維數組(見圖9) 將具有某種關系的任何兩個頂點連接在一起。數組dis表示起點和其他點之間的距離，其初始值為[0，2，6，4]。數組簿表示是否數組dis所對應的距離是最短，其初始值為[1，0，0，0]。Dijkstra優化理論的目的是獲得起點與其他點之間的距離，選擇距離點1最近的點2作為下一個搜索點。在圖9所示的二維數組中，所有項都是正數，如果選擇另一個點作為下一個搜索點，則距離一定會比點2和點1之間的距離更長。數組簿更新為[1，1，0，0]，然后檢查是否存在通過點2到達起點1的任何其他點間的距離短于點2與點1之間的距離。可以發現，dis[3]=6，dis[2]+edge[2][3]=5<6，dis更新為[0，2，5，4]。重復上述更新過程，可以在每次迭代計算后獲得中間點和起點之間的距離。因此，最多執行3次更新過程，便可得到優化結果。

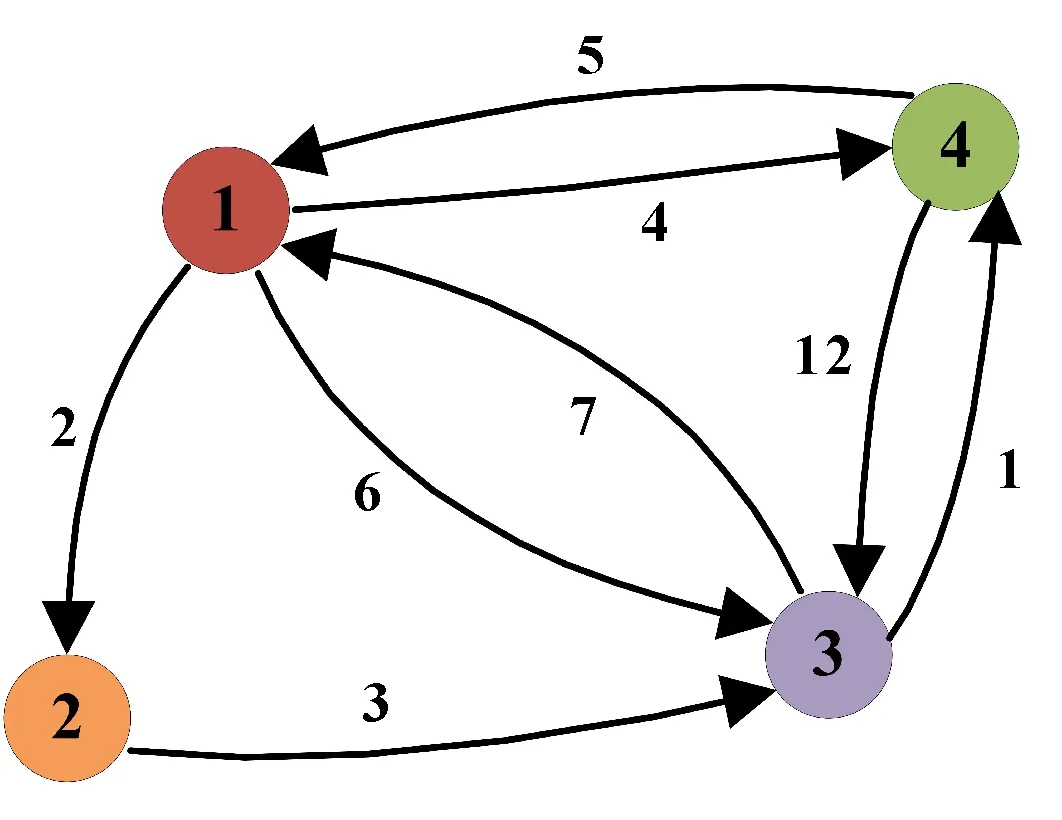
圖8 Dijkstra優化理論的搜索優化過程示意

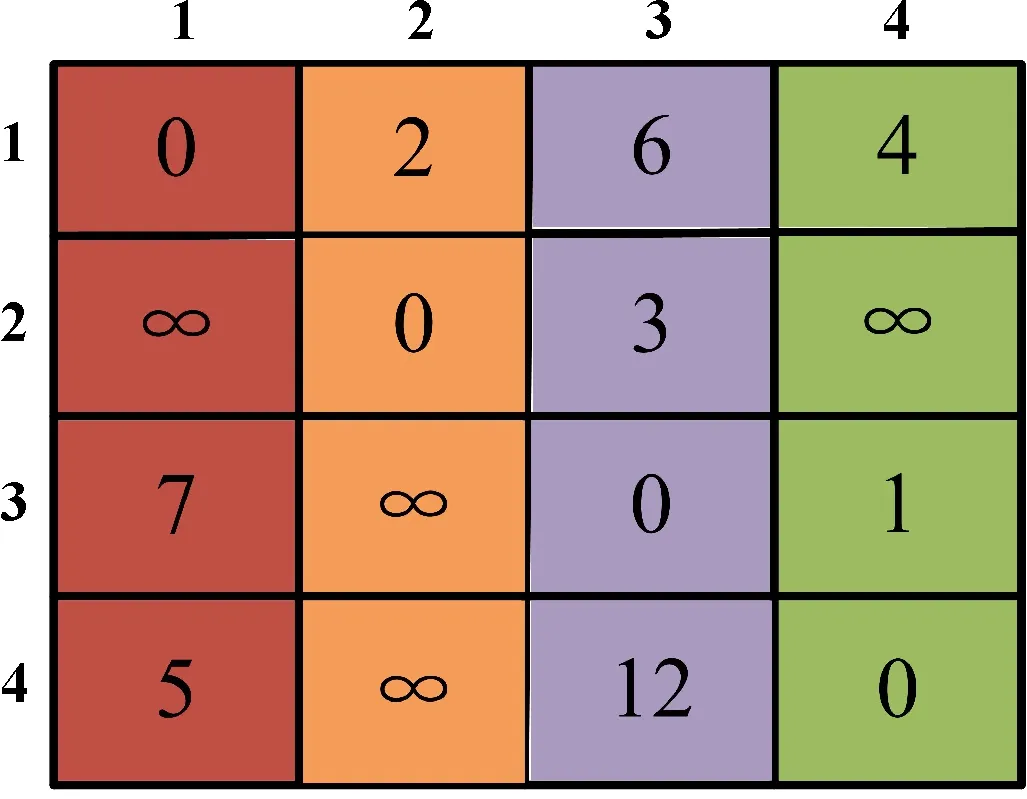
圖9 Dijkstra優化理論中的數組

為在石材雕刻機械臂可達工作空間內，尋優得到運動性能最優的工作空間，設計Dijkstra優化理論的執行流程如圖10所示。

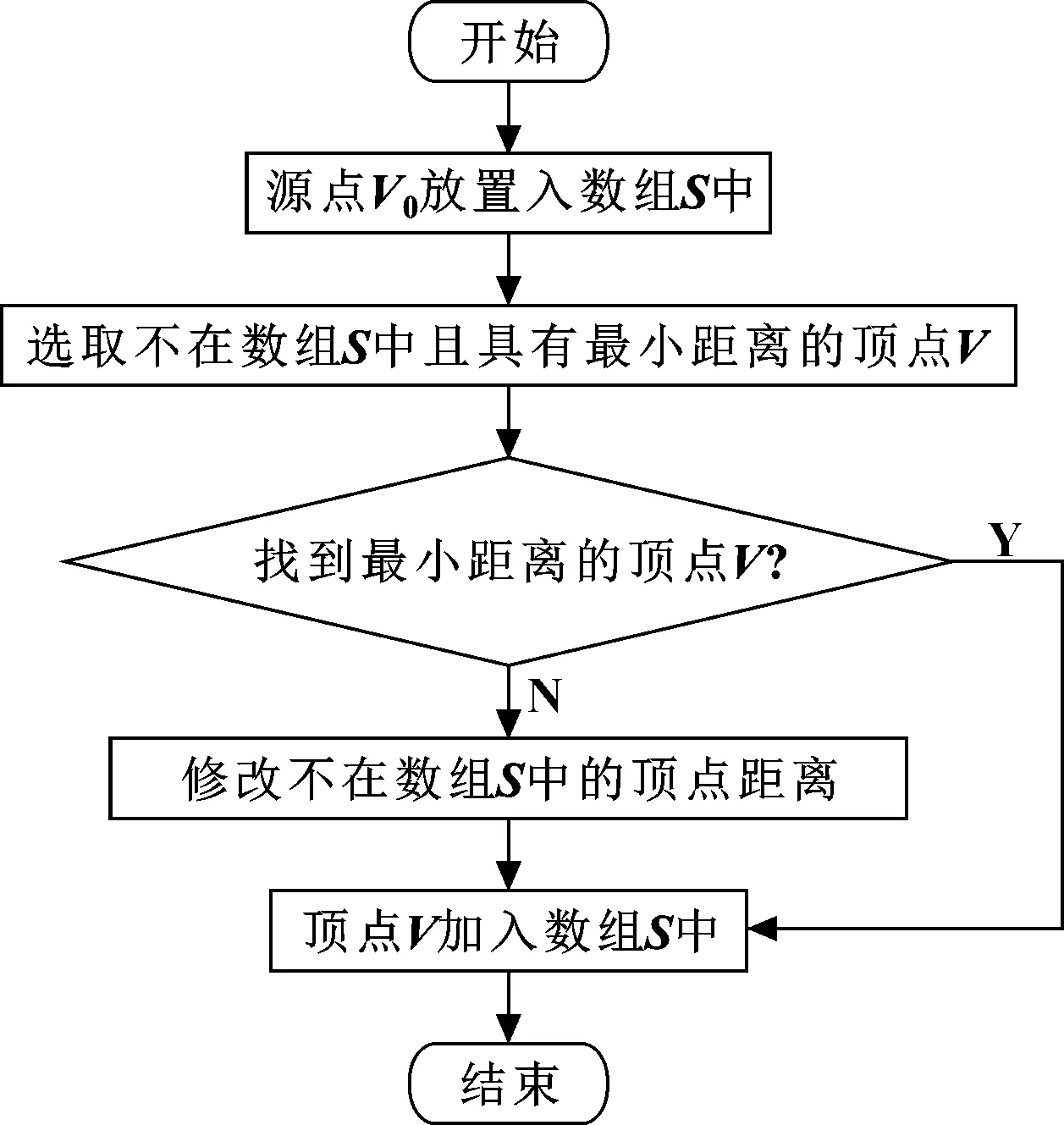
圖10 Dijkstra優化理論的執行流程

步驟1，初始時，數組只包含源點，即={}，與其他頂點的距離為0。數組包含除外的其他頂點，即={其余頂點}，若與中頂點有共邊，則<,>正常有權值，若不是的共邊鄰接點，則<,>權值為∞;

步驟2，從數組中選取一個距離最近的頂點，把加入中(該選定的距離就是到的最短路徑長度);

步驟3，以為新考慮的中間點，修改中各頂點的距離；若從源點到頂點的距離(經過頂點)比原距離(不經過頂點)短，則修改頂點的距離；

步驟4，重復步驟(2)和(3)，直到所有頂點都包含在數組中。

根據上述設計步驟，將石材毛坯內216個步數點的靈巧度逐步累加求和得到區域靈巧度，經過尋優得到值最大的區域即為目標加工區域。經過尋優計算得到，石材雕刻機械臂在其可達工作空間內靈巧度最大的5個點分別為(500,1 500,100)、(400,1 500,100)、(300,1 600,100)、(0,1 600,100)、(0,1 600,100)，其靈巧度分別為0.174 57、0.174 53、0.174 51、0.174 50、0.174 45。將這5個點 (=1,2,3,4,5)作為源點，可達空間內其余1 326個點作為數組；選取中相對中靈巧度兩者差值最小的點加入中，以此類推，將每個源點逐漸擴展至與預優化空間幾何形狀和大小相同的點集，計算每個的值。經過計算，石材毛坯內216個步數點，最大靈巧性值=33.475 65，位于∈[-300 mm,200 mm]、∈[1 500 mm,2 000 mm]、∈[100 mm,600 mm]的幾何區域，如圖11所示。

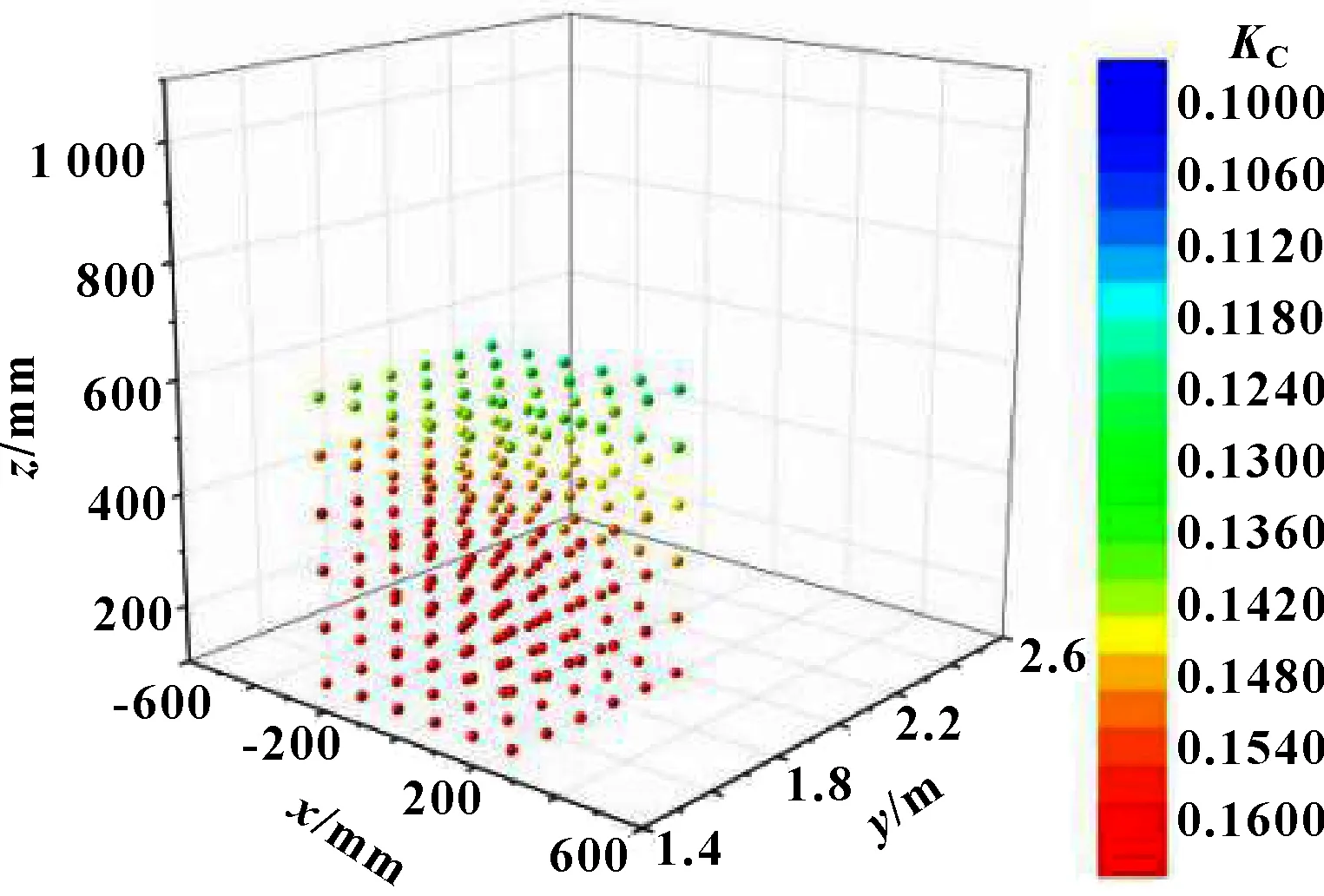
圖11 石材雕刻機械臂最優工作空間

4.2 優化結果驗證

石材雕刻機械臂是一個復雜的非線性系統，每個關節都會相互作用，因此很難直接在ADAMS軟件中建立其3D模型。為驗證優化結果的正確性，在3D設計軟件SolidWorks中建立KR240-R2900機械臂模型和HSD末端執行器模型，并將所建立的模型以特定格式導入到ADAMS中。最后，建立一個可正確表征雕刻機械臂在石材雕刻過程中運動性能的動態模型。模型建立的具體過程如下：

(1)石材雕刻機械臂模型裝配

末端執行器的實物如圖12(a)所示，根據實際尺寸，在SolidWorks中設計的末端執行器的三維模型如圖12(b)所示。將機械臂主體與設計的末端執行器裝配在一起，如圖13所示，將裝配配合約束添加到石雕機械臂的相鄰組件中(機械臂基座，腰關節，大臂關節，小臂關節，肘關節和末端執行器)。為使石雕機械臂裝配模型可導入ADAMS中，在SolidWorks中將其模型保存為parasolid (*.x_t)格式。

圖12 石雕機械臂末端執行器模型

圖13 石材雕刻機械臂的裝配模型

(2)ADAMS中的仿真參數設置

①仿真環境設置

HSD末端執行器是由45鋼制成。經過多次相關標定試驗后，將末端執行器的材料密度設為7.801×10kg/mm，將其彈性模量設為2.07×10N/mm，泊松比設為0.29。然后，基于建立的裝配模型，計算其各組成部分的動態特性參數，并對各關節進行校正試驗，表2所示為石材雕刻機械臂的最終動態特性參數。該表包含了仿真所用到的石材雕刻機械臂每個連桿質量、質心與慣性矩的信息。

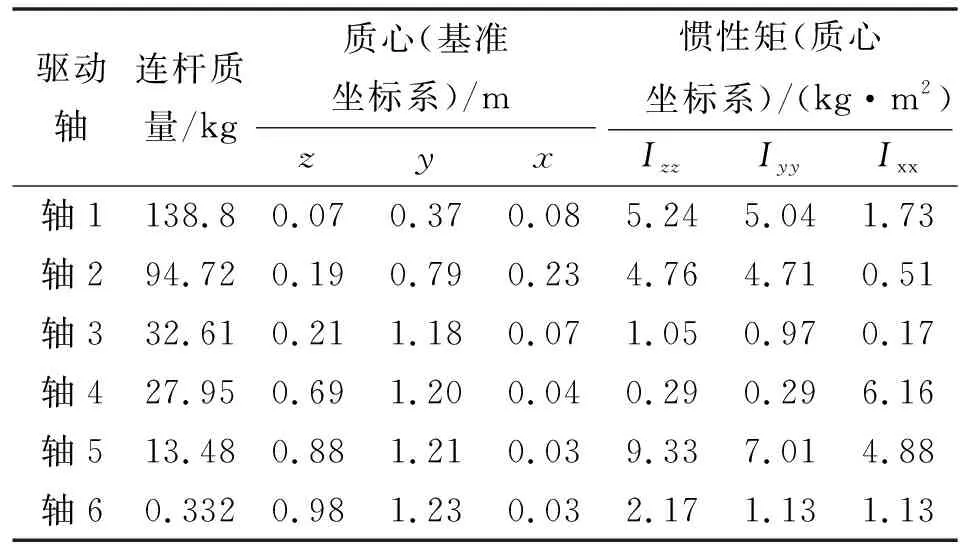
表2 石材雕刻機械臂組成部分的動態特性參數

②關節驅動設置

石雕機械臂基座和大地坐標之間的關系是固定的，關節6和末端執行器之間的關系也是固定的，因此將它們的關節連接方法設置為固定副。此外，相鄰關節 (軸1，軸2，軸3，軸4，軸5，軸6) 之間存在偏轉運動，將它們的關節連接方法設置為旋轉副。然后，創建石雕機械臂每個關節的角度函數作為用于驅動設置的各關節驅動函數。將前文中的角度函數導入ADAMS軟件中，以創建位于數據單元中的SPLINE函數。最后，配合使用SPLINE函數與ADAMS中內置的“Cubic Fitting Method”就可以驅動石材雕刻機械臂運動。

③仿真與測量

設置好驅動函數和仿真時間(12 s)后，可以在ADAMS中模擬石材雕刻機械臂的運動過程。根據實際要求，測量石雕機械臂每個關節的角速度和角加速度，并在后處理窗口中獲得每個關節的測量變化曲線。在該窗口中，可以導出測量變化曲線，也可以將外部數據導入到ADAMS中，從而實現不同變化曲線的比較。在3個不同加工位置，石材雕刻機械臂均以相同回字形軌跡和2 000 mm/min的進給速度運動，如圖14所示。按照文中所提到的方法，計算不同加工位置(No.1、No.2和No.3)的總靈巧度，結果如表3所示。位置1 (No.1)是通過Dijkstra理論優化的加工位置，位置2(No.2)和位置3(No.3)是石雕機械臂可達空間中選取的任意加工位置。在3個位置(No.1、No.2和No.3)、6個關節角速度～和角加速度～的變化曲線分別如圖15和圖16所示。方差值～、～分別如表4、表5所示。

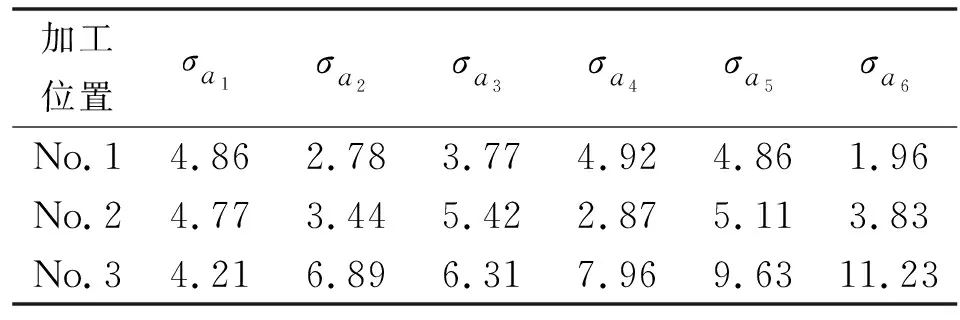
表5 不同加工位置的角加速度性能對比

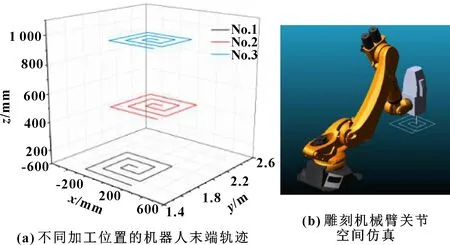
圖14 石材雕刻機械臂雕刻過程仿真

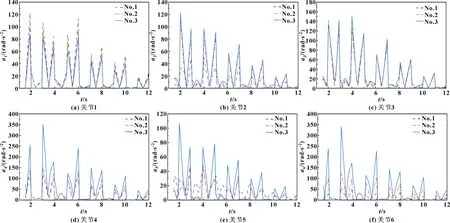
圖16 石雕機械臂各關節角加速度的變化曲線

表3 不同加工位置的靈巧度對比

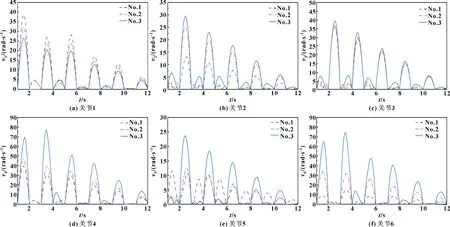
圖15 石雕機械臂各關節角速度的變化曲線

如圖15和表4所示：除石雕機械臂關節1外，其他關節位置No.1處的速度最大值與方差值均明顯小于加工位置No.2與No.3,且隨著靈巧度指數的增加，石雕機械臂的運動性能變強。以最影響石雕機械臂運動性能的關節2為例，在機械臂運動性能最優的位置No.1處進行加工，相比于位置No.3處，角速度方差減少了60.6%。各關節角速度方差的減少，不僅可以提高石雕機械臂的作業效率，同時也可以降低加工時的能量消耗。

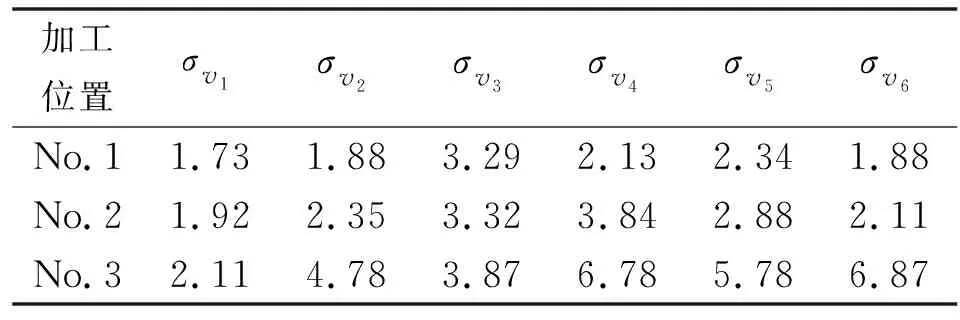
表4 不同加工位置的角速度方差

如圖16和表5所示：石雕機械臂在最優加工位置No.1處運動時，除了關節1外，其他關節的角加速度方差也均明顯小于加工位置No.2與No.3，進一步驗證了優化結果的有效性。在位置No.1處運動時，關節2的角加速度方差僅為2.78，比它在位置No.3處運動時減少了59.6%；在位置 No.1 處，關節3的角加速度方差僅為3.77，比它在位置No.3處運動時減少了40.2%。各關節角加速度方差的減少，不僅可以提高石雕機械臂的運動脈沖，也可以減少加工中的沖擊，有利于提高跟蹤精度，保護機械結構。

5 結論

(1) 基于D-H參數法建立了所研究的石材雕刻機械臂的運動學模型，并通過旋量理論中的指數乘積公式推導出了石材雕刻機械臂正運動學解和逆運動學解。

(2) 基于雅克比矩陣的條件數，提出了一種可以定量描述石材雕刻機械臂運動性能的指標(靈巧度)，并進一步研究了靈巧度指標在關節空間坐標和操作空間坐標下的變化規律。結果表明：隨著石雕機械臂不斷向外延伸(方向位移增加)，其運動性能會降低，且在其可達空間內，-橫截面的整體運動性能隨著雕刻加工的進行(即高度逐漸減小)而提升。

(3) 基于Dijkstra優化理論，設計了石材雕刻機械臂最優工作空間的優化目標與優化流程。仿真結果表明：當石材雕刻機械臂在其最優工作空間中工作時，其關節角速度的波動會減少60.6%，關節角加速度的波動會減少40.2%。證明了文中算法的有效性，可為石材雕刻機械臂加工位置的布局提供參考。