襯套壓裝機傳動系統動力學建模與抖動控制研究

武卓，曹家勇，許海波，吳沛華

(上海應用技術大學機械工程學院，上海 201418)

0 前言

汽車渦輪增壓器閥芯孔襯套壓裝(以下簡稱襯套壓裝)是一種典型的壓裝工藝，傳統襯套壓裝機多為液壓驅動，其壓裝過程難以精確控制。隨著汽車產品質量要求日益嚴格，對襯套壓裝工藝提出越來越高的要求。于是，具有高定位精度和靈活可控性的伺服驅動系統被應用到壓裝機，因為軌跡得到精確控制，所以壓裝精度和抗干擾性能得到較大提高。

目前，國內外針對伺服壓裝系統的研究多為機械結構設計和設備的選擇，通過提高設備的精密性來提升壓裝質量。上海交通大學的劉昊旻設計了差動伺服壓裝系統，差動式壓裝方法有效減少壓裝過程對零件裝配的影響。合肥工業大學的孫國兵通過對零部件的測量和壓裝工藝的計算，選出適合的電缸和設計壓裝設備需要的零部件。西安交通大學的ZHENG等提出了一種基于自調整PID控制器伺服壓力機的方案。

從壓裝工藝本質來說，襯套與閥芯孔之間屬于過盈配合，配合表面間材料的擠壓作用不可避免地帶來非線性摩擦阻力特性，從而經常性地造成壓裝傳動系統出現嚴重的抖動現象，對產品的質量和設備的安全造成極大危害。壓裝抖動現象有兩種解決途徑：一種是從傳動系統設計的角度，另一種是從控制系統算法的角度。由于不需要變更機械硬件組成，后者具有更大的柔性和更低的成本，具有很好的研究價值。

壓裝過程是一個復雜的機械運動過程，且壓裝過程中存在外界干擾和自身固有的非線性，因此壓裝過程的動力學模型過于復雜且難以建模。故現今關于伺服壓裝中的非線性摩擦特性及其抖動現象的研究文獻很少。另一方面壓裝機每裝配一個零件，就需要重復一次壓裝過程，因此，壓裝機工作狀態可以看作一個重復過程。過程重復并且難以建立精確的動力學模型，故采用迭代學習控制來不斷優化和提升性能是很好的策略。

迭代學習控制通過迭代不斷學習，從而調整輸入來不斷地減小跟蹤誤差，最終使得系統實際輸出非常接近理想輸出。迭代學習控制可以構建目標函數來加快迭代速率。最近幾十年里，迭代學習控制研究迅速，在相關技術領域發展成熟且廣泛應用于機器人和工業機床等行業。綜上，本文作者提出采用迭代學習控制策略來抑制伺服壓裝系統中出現的振蕩現象。為體現所采用算法的有效性，對控制算法和系統動態特性進行仿真比較研究。

1 壓裝過程動力學建模

1.1 現場伺服壓裝機存在壓入抖動現象

作者研發的已經應用于實際生產線的汽車渦輪增壓器閥芯孔襯套壓裝機局部如圖1所示，結構簡圖如圖2所示。設備主要由伺服電機、滾珠絲杠、同步帶、壓力傳感器、壓頭組件、夾具、機架等組成。壓裝過程是先通過定位夾緊組件對待加工的渦輪殼進行定位與夾緊，接著由伺服電動缸傳輸動力控制壓裝組件，壓裝組件向下移動，將裝夾在壓頭的襯套與渦輪殼閥芯孔實現無鍵過盈配合，完成零件的裝配，最后壓裝組件回到原位。壓裝組件不斷往復(上下移動)工作，實現大量零件的裝配。

圖1 汽車渦輪殼襯套伺服壓裝機局部

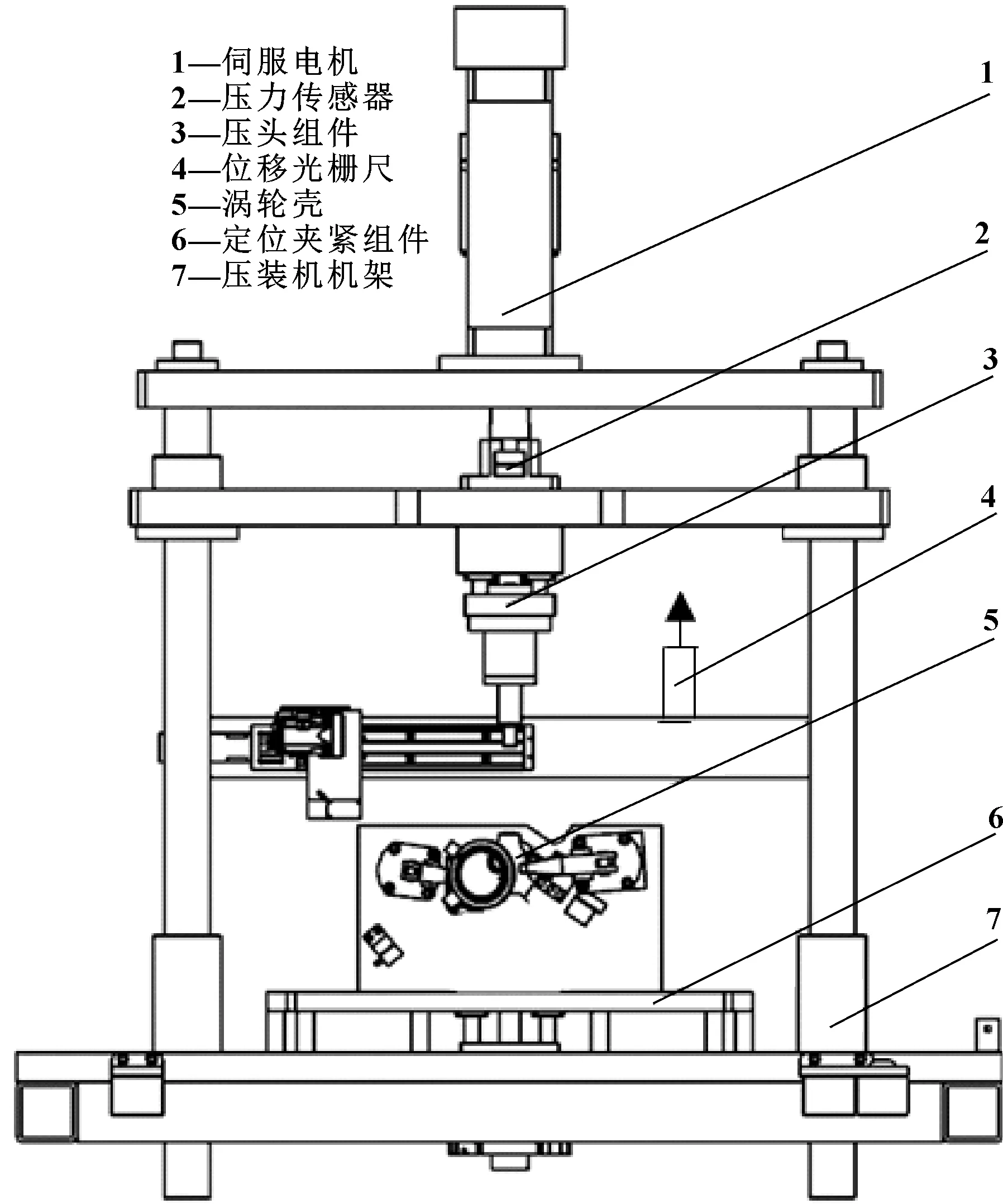
圖2 壓裝機結構簡圖

因為在壓裝過程中襯套與閥芯孔產生的摩擦力較大，受摩擦作用較其他部分更加明顯，因此主要考慮襯套與閥芯孔間的摩擦對系統的影響。在設備實際運行過程中，所記錄的壓力位移曲線顯示設備經常性出現抖動或爬行現象，如圖3所示。

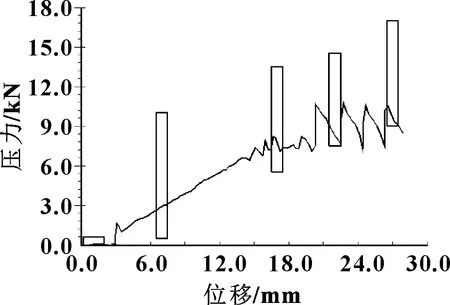
圖3 存在抖動問題的位移壓力曲線

1.2 傳動系統動力學方程

為了使建立的數學模型合理，對壓裝機的機械傳動結構進行分析，將其分為若干個獨立組件，依據動力學原理進行建模。其中壓裝機的機械部件有軸承、絲杠、滾珠和螺母組件等，由伺服電機輸出扭矩通過同步帶傳遞給絲杠，絲杠將旋轉運動轉換為螺母的直線運動，使壓頭組件做上下直線運動。對于伺服壓裝系統的彈性系數和阻尼系數，主要考慮同步帶的參數。為簡化模型，揭示機制，將外部影響因素和壓裝過程抽象為彈簧阻尼系統，如圖4所示。

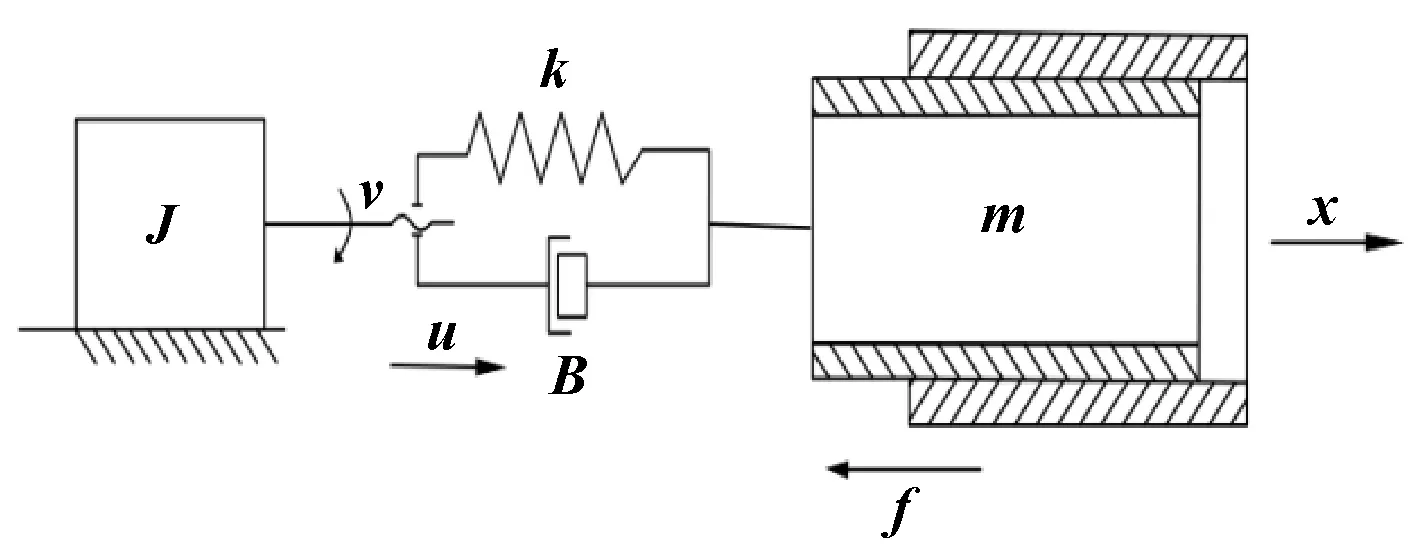
圖4 壓裝過程簡化模型

根據動力學原理，建立動力學方程如下：

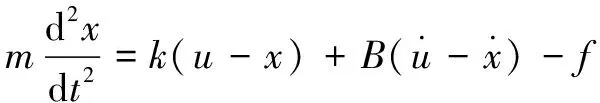
(1)

對于一個線性時不變的連續受控系統，其狀態方程為

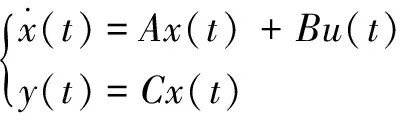
(2)

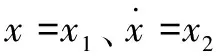
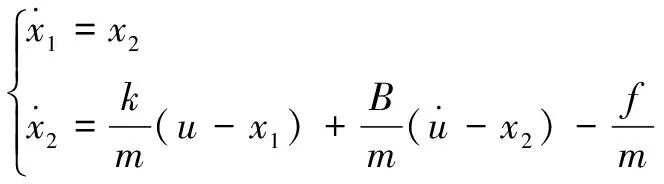
(3)

則系統狀態空間方程為

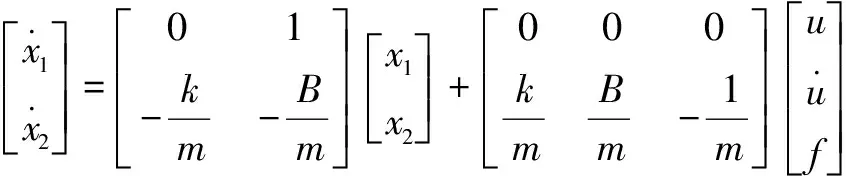
(4)

式中:為壓頭和襯套的質量;為襯套壓入位移;為電機經同步帶到絲杠的等效輸入位移;為同步帶的彈性系數;為同步帶黏性阻尼系數;為襯套所受到的摩擦力。

1.3 壓裝面非線性摩擦模型

圖3表明襯套外圓面與渦輪殼孔壁之間存在非線性摩擦現象。20世紀初，STRIBECK等通過實驗觀察到低速下摩擦力的特性，如圖5所示。可以看出：在低速運動時，摩擦力呈現回落的特性，具有非常明顯的非線性。這種曲線稱為Stribeck曲線。

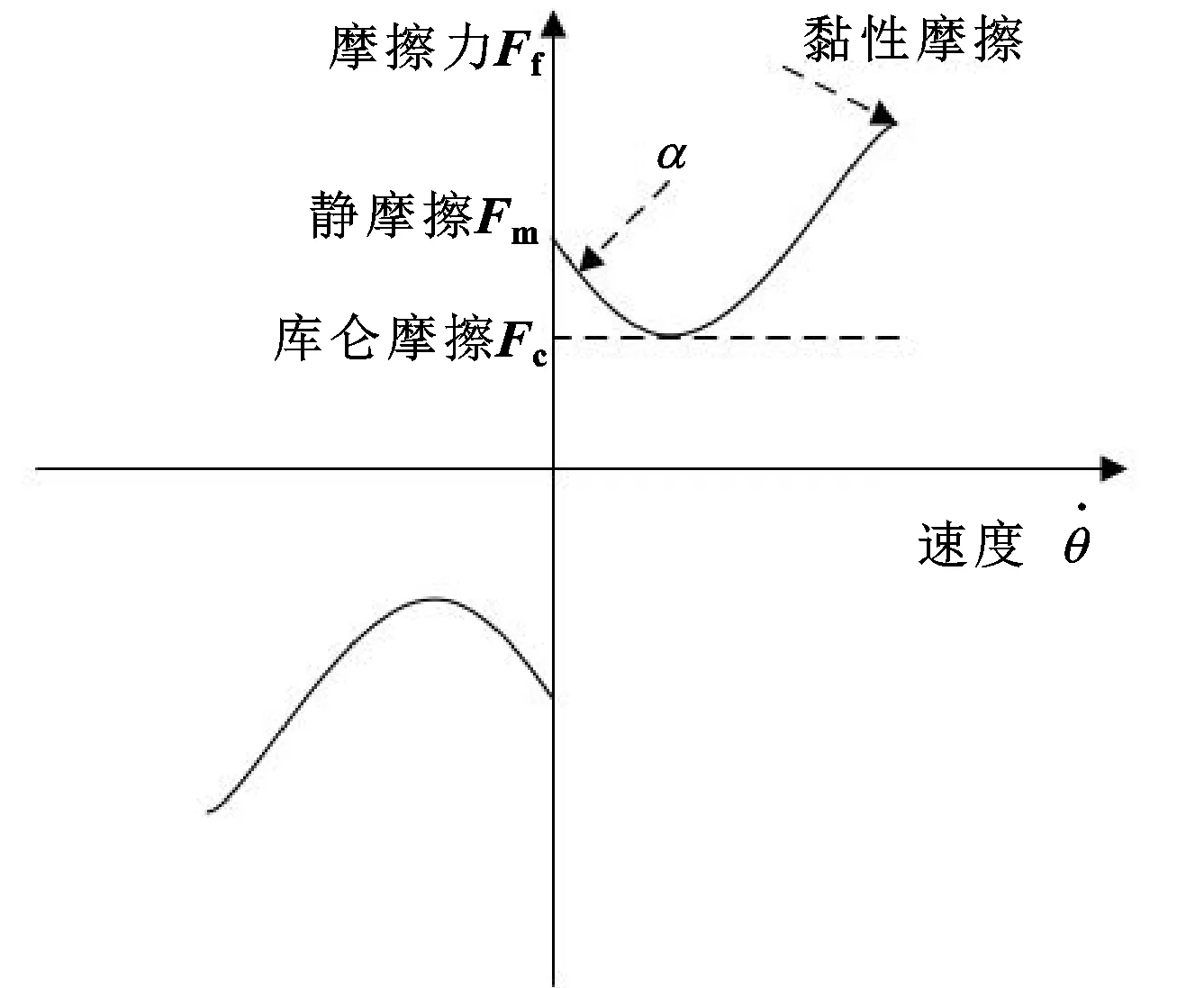
圖5 Stribeck曲線

Stribeck實驗已經證明該模型能以90%的精度近似真實的摩擦力。Stribeck摩擦模型能夠很好地反映壓裝過程中非線性部分的運動特性，故而在選模型期間，將壓裝的摩擦模型定義為Stribeck摩擦模型。它的具體表達式如下所示：

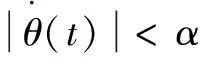
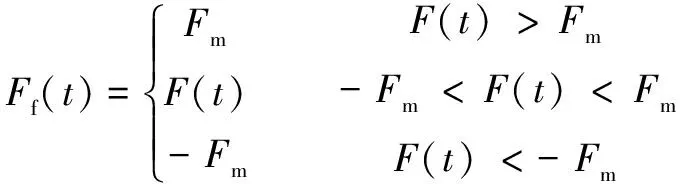
(5)

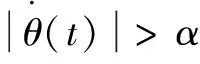
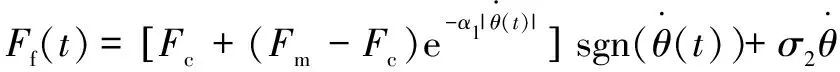
(6)

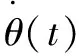
2 壓裝過程迭代學習控制器

本文作者采用PD型迭代學習算法，結構如圖6所示。

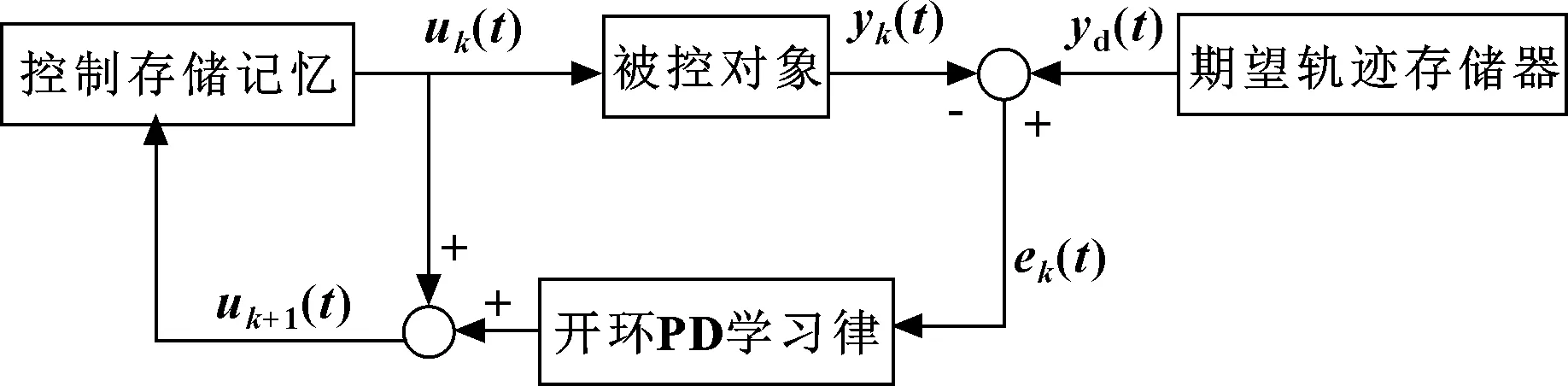
圖6 PD迭代學習控制的結構

PD型迭代學習控制的策略是：第+1次的輸入等于第次輸入加上第次輸出誤差的矯正項，即

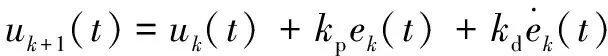
(7)

≤≤(+1),=0,1,2…

(8)

其中，跟蹤誤差

()=()-()

(9)

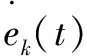
迭代學習算法是否收斂決定了該算法的有效性，只有迭代學習過程是收斂的，控制系統才不會發散。若迭代學習算法收斂，即當趨向無窮時，跟蹤誤差在[0,]上趨于零，系統輸出才會趨近期望的軌跡。根據PD型迭代學習律，只要找到合適的、值，就可以使迭代學習算法收斂且實際輸出非常接近理想輸出。若、為常數矩陣，為單位矩陣，為收斂半徑，則、應滿足收斂條件：

|(-)|)<1∈[0,]

(10)

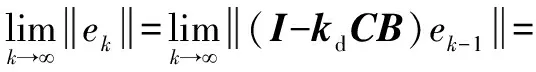
(11)

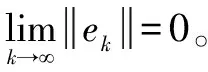
迭代學習控制通過改善輸入來提高系統跟蹤能力，即給定期望壓入位移()和每次運行的初始狀態(0)，按照學習控制算法通過多次迭代學習(多次加工過程)，得到理想的控制輸入(),使得系統輸出()→()。

迭代學習控制流程如圖7所示。圖中為系統的傳遞函數，為迭代次數。

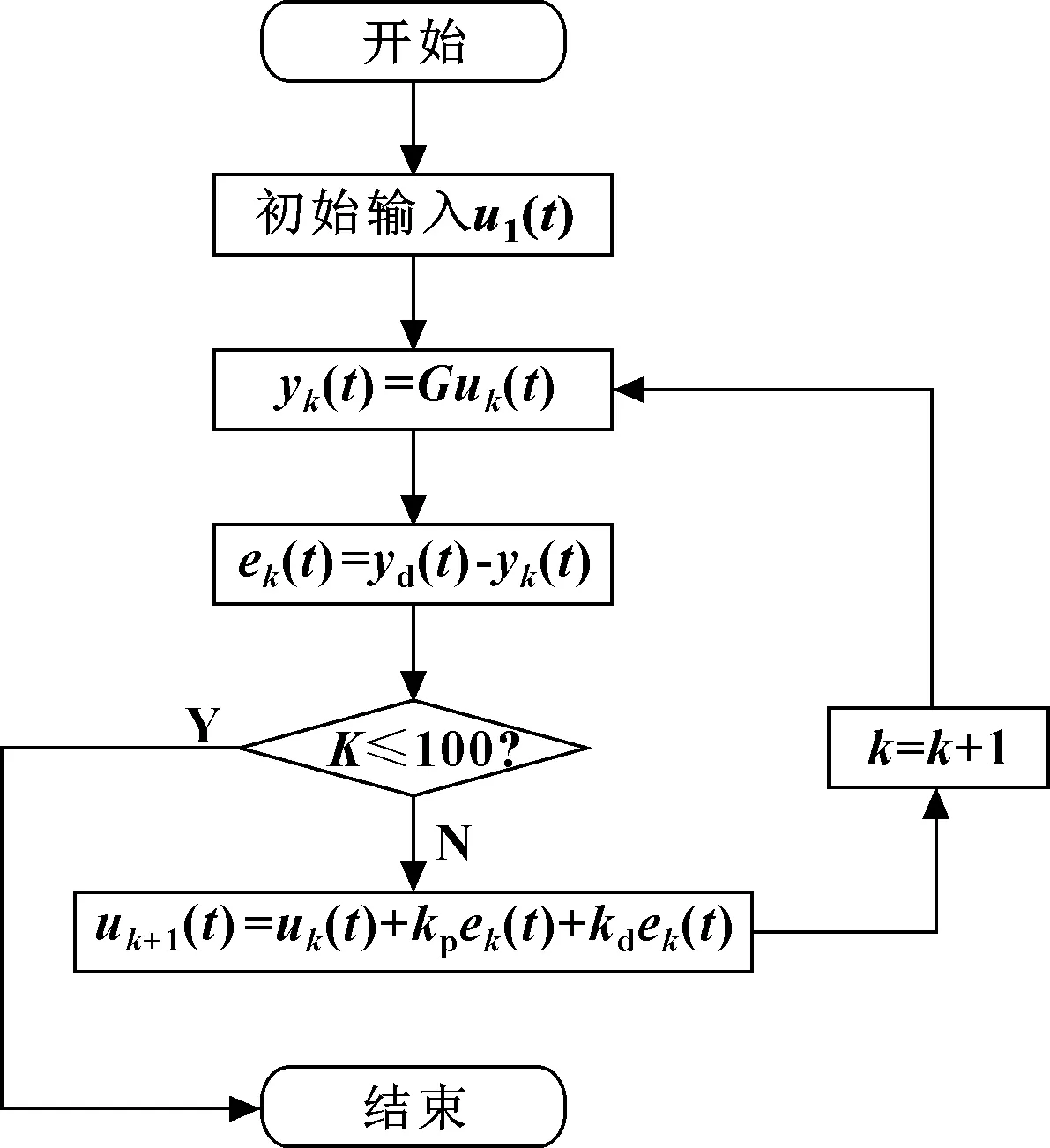
圖7 迭代算法流程

3 數值仿真驗證

3.1 非線性爬行現象仿真

圖8是與圖5對應的Simulink摩擦模型，該模型是從參考文獻[11]拓展而成的。為了體現靜摩擦力，在該模型中定義了一個零速區間，當||<(1×10)時前饋通道接通，抵消了控制輸入()，前饋通道有飽和特性，其飽和值等于最大靜摩擦力；當||≥，即()>時，負載開始運動，代表動摩擦力。將此摩擦模型封裝成一個子系統應用到壓裝中，并在Simulink中進行仿真。

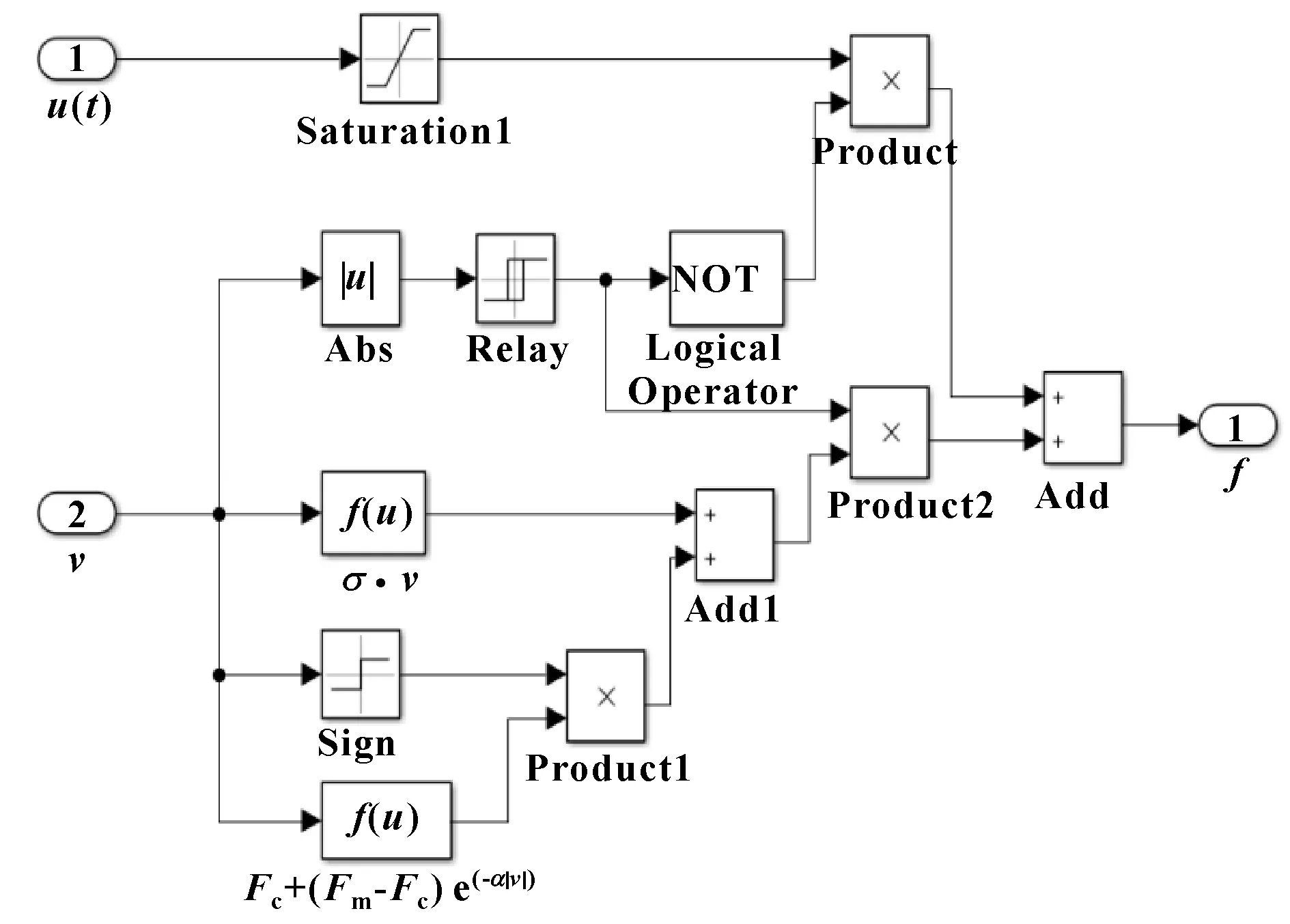
圖8 摩擦的Simulink模型

從圖9可以看出：襯套有明顯的抖振及爬行現象。圖10為仿真時襯套壓入的摩擦力，圖像大致與圖3后半部分差不多，說明用改進的Stribeck模型來描述襯套和渦輪殼閥芯孔摩擦特性，尤其是黏滑運動是可行的，這也表明伺服系統用此模型來描述非線性摩擦所得的仿真結果是可信的。

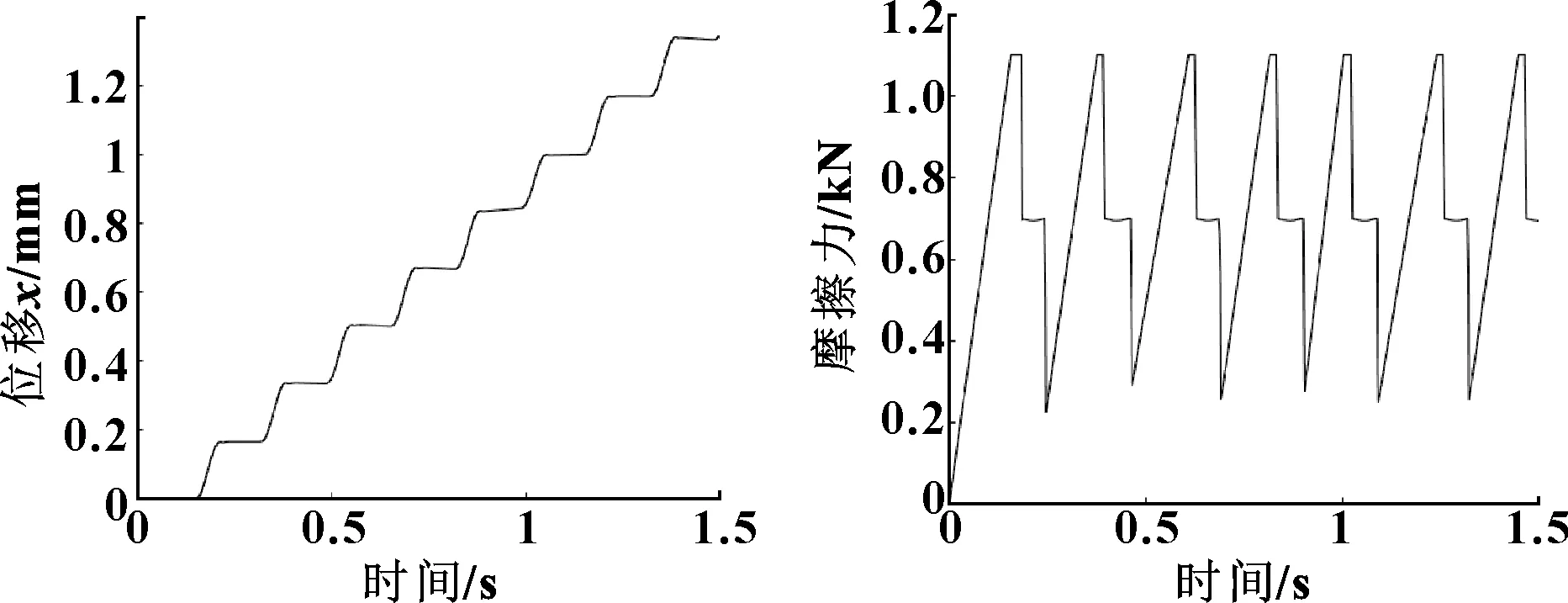
圖9 壓裝過程中的低速爬行現象 圖10 襯套壓入時摩擦力曲線

3.2 迭代控制仿真驗證

通過MATLAB里的Simulink軟件來實現迭代學習控制的仿真，把MATLAB的工作區作為一個存儲器，存儲每次的誤差和實際輸出，下次迭代時，迭代學習律依據上次的誤差調整實際輸入。圖11為迭代學習控制伺服壓裝系統的仿真模型。為了凸顯使用迭代學習控制在伺服壓裝系統的優勢，給出了PID算法的控制效果。

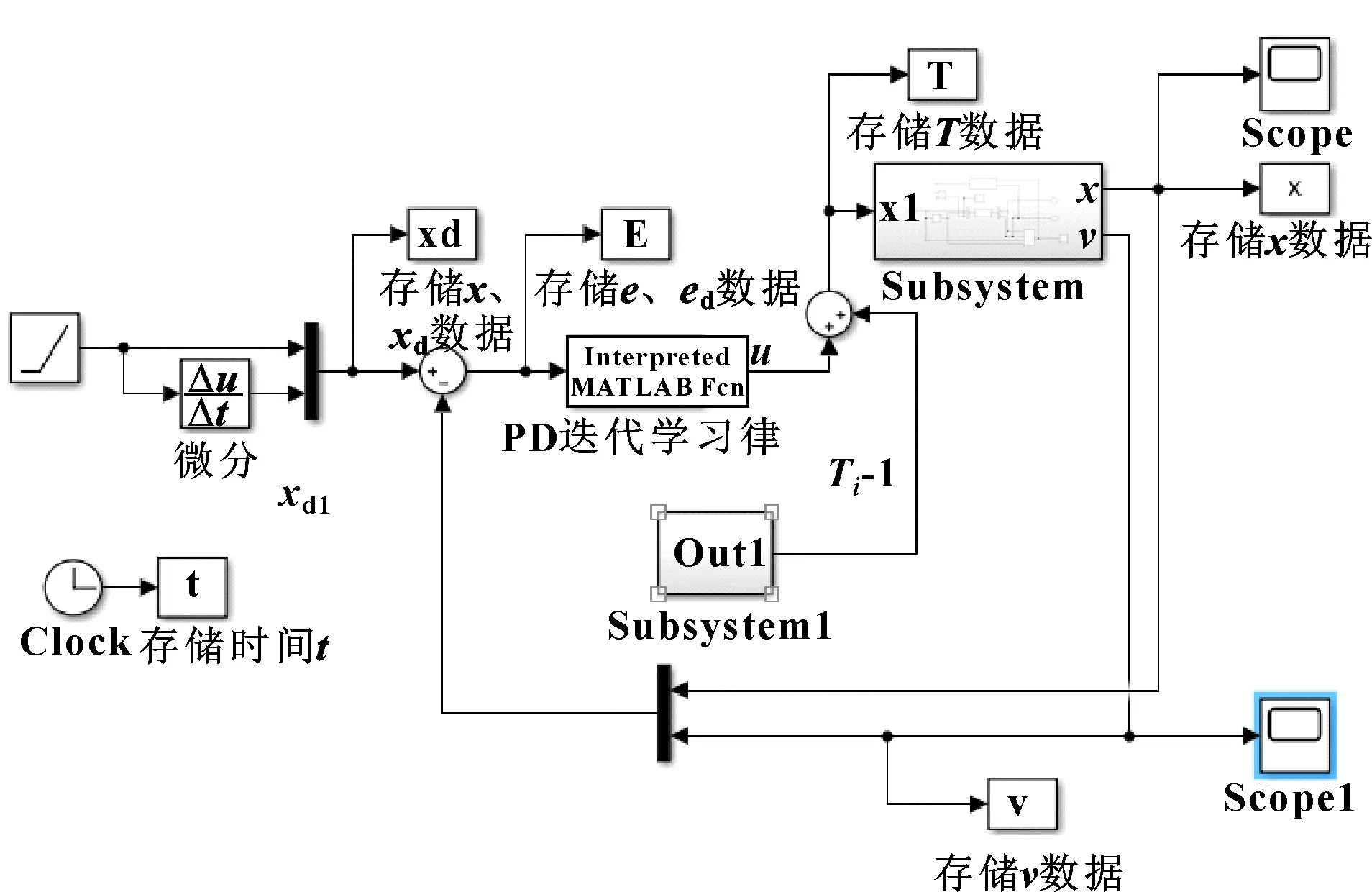
圖11 控制系統的仿真模型

系統參數如表1所示。

表1 系統仿真參數

表中壓頭和襯套的等效質量為設備實際參數，同步帶等彈性系數、阻尼系數、襯套與閥芯孔的最大靜摩擦力、庫侖摩擦力通過實際參數和公式計算得到，黏性摩擦力比例系數、零速區間、常數參考文獻[13]。

采用PD型迭代學習控制算法，迭代學習系數=10、=0.5，PID參數為10、為10、為0.5。輸入信號為階躍信號。從圖12觀察出使用這兩種算法系統都是穩定的，PID控制存在靜態誤差。

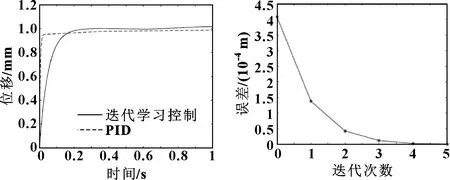
圖12 兩種控制算法的階躍響應 圖13 最大誤差絕對值與迭代次數的關系

輸入信號為斜坡信號()=0.001，位移跟蹤最大誤差絕對值與迭代次數的關系如圖13所示。可以看出：隨著迭代次數的增加，位置跟蹤誤差在不斷減小。第1次迭代最大誤差值為0.130 mm，第4次迭代的最大誤差值為0.043 mm，第5次迭代的最大值為0.010 mm，5次迭代以后的最大誤差值變化幅度很小。表明隨著迭代次數增長，位移跟蹤誤差收斂于真值。為了減小非線性摩擦對系統的影響，迭代次數選取大于5次。

對比圖14和圖15可以發現：兩者都可以抑制低速下的爬行現象，但迭代學習控制通過迭代減小誤差達到0.010 mm；而PID誤差絕對值為0.013 1 mm。迭代學習控制相比PID控制精度提高了30%，更加逼近期望曲線，表明了迭代學習控制相比PID控制有著更高的位移跟蹤精度。

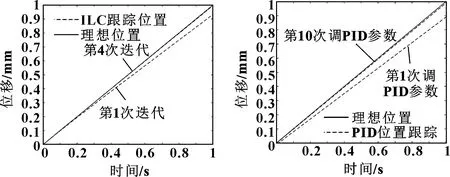
圖14 迭代學習控制位移跟蹤曲線 圖15 PID控制位移跟蹤曲線

考慮電機的功率，在仿真模塊中，將驅動力限幅為20 kN。為了體現算法的處理性能，給予初始速度為0.001 m/s，并且在0.6 s時刻給予相當于30%摩擦力的外力干擾。圖16所示為迭代學習控制和PID控制速度跟蹤曲線，可以看出：若系統參數發生微小的變化，迭代學習控制曲線波動較小；而在同樣條件下的PID控制所得到的響應曲線有很大的波動。說明迭代學習控制相比PID控制對伺服壓裝系統適應性更好，并且由于非線性摩擦等因素影響，PID控制的速度跟蹤曲線有一定靜態誤差；另一方面，面對外界干擾時，迭代學習控制有著更小的振蕩幅度、更快的響應速度。

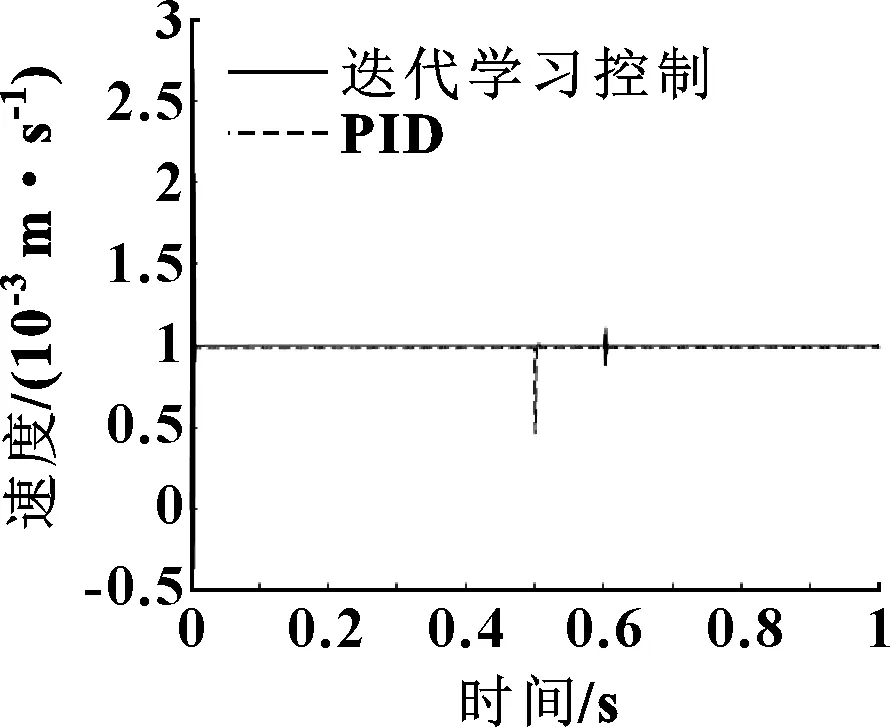
圖16 ILC和PID控制速度跟蹤曲線

4 結論

現場的汽車渦輪增壓器襯套壓裝設備工作時存在較頻繁的壓入抖動現象，對產品質量造成極大危害。為揭示此類現象的機制，基于機械系統動力學理論，采用經典Stribeck非線性摩擦模型刻畫襯套和襯套孔之間的相互作用力，建立了壓裝傳動系統動力學模型，得到了襯套壓入過程速度波動曲線和壓入力波動曲線。通過對比發現：所述曲線具備了與現場采集數據基本一致的振蕩特征，說明振動模型具有較好的可行性，為抑制壓裝過程的抖動現象、提升產品加工質量，提供了壓裝精密伺服控制思路。考慮到襯套壓裝過程是一類典型的不斷重復的自動機械加工過程，采用迭代學習(ILC)控制理論設計了壓裝過程控制算法，對控制器參數進行學習優化。仿真結果表明：相比于一般的PID控制算法，迭代控制策略在抑制抖動爬行、抵抗外界干擾、提高伺服系統跟蹤精度等方面具有較優的性能。