小學數學工具在課堂教學中的實踐應用

文／孫振陽

引 言

探索性活動離不開數學工具的支持，數學工具在學生的探索實踐中起著十分重要的作用[1]。數學工具應用的過程也是學生創造性地解決問題，真正經歷和體驗探索的過程[2]。數學工具的使用可以將抽象的數學知識直觀化、具體化、形象化。學生在使用數學工具的過程中，能獲得感性認識和直觀經驗，理解和掌握數學知識，更好地發展數學思維。

一、數學工具應用的策略思考

（一）關注趣味性與實踐性

數學工具的使用可以激發學生對數學學習的興趣，讓學生在實踐操作中，自主快樂地開展學習活動。例如，在學習“認識厘米”時，學生可將身邊一切可以利用的生活材料及自己的身體作為數學工具，如尺子、橡皮、鉛筆、手指等。這樣學生對概念的認識就不止停留于教師抽象的講解，而是借助數學工具在比較、判斷、實踐中加深理解。這樣的學習更富有趣味，更能調動學生學習的主動性，有助于學生對概念本質的深入認識。

（二）關注適切性與適度性

教學中所選擇的工具要符合小學生的年齡特征，符合學科特點，便于學生使用和操作，進而為教師教學服務。例如，從兒童的認知特點看，小學生在學習過程中更關注“有趣、好玩、新奇”的事物，為此，在教學蘇教版數學三年級（上冊）“平移和旋轉”時，筆者在學生初步認識了平移后，組織學生開展“推箱子”游戲活動，并讓其交流在操作中應用了哪些剛學習過的知識。推箱子操作很好地激發了學生的學習熱情。接著，在“認識旋轉”的導入環節，筆者拿出一個小電風扇，讓學生初步感受旋轉現象，然后讓學生觀察扇葉是怎樣運動的，嘗試用手勢比劃出來。小電風扇這一工具的使用和推箱子游戲演示都給予了學生指導。教師要認識到雖然工具的使用調動了學生的學習積極性，但不能讓課堂變成吹電風扇和玩游戲，而要注重適度與適切性，利用工具某一方面的特質，讓它為課堂所用。

（三）關注工具性與思維提升

數學工具可以輔助教學，在學生認識的重難點及關鍵點給學生以合適的幫助，讓學生更好地理解所學知識。但是在教學過程中，教師不能一味地依賴數學工具，形成依賴后會讓學生在遇到相同或類似問題時必須使用工具[3]。教師應認識到數學工具可以作為教學的輔助性手段，而不是教學的必要手段。學生在利用數學工具進行操作實踐后要思考交流，提煉問題的本質，促進思維的提升。例如，在蘇教版數學四年級（上冊）“可能性”的教學中，筆者給學生提供了一個不透明的口袋，里面裝了除顏色外，其他完全相同的一個紅球和一個黃球，讓學生分成4 人小組，每個小組摸10 次，記錄摸球的數據。但摸球實驗不是學習這一課的目的，而是通過摸球實驗收集數據，對數據進行分析。在學生摸完球后，教師對學生進行提問：“都是摸10 次，為什么每個小組摸到紅球與黃球的次數并不完全相同？”“奇怪了，同樣是第一次摸，為什么有的是紅球，有的是黃球呢？”“咱們再來觀察，第3 組和第8 組都是5 紅5 黃，每次摸球的顏色都相同嗎？”通過這些問題的交流，學生認識到每個小組摸到紅球和黃球的次數和次序并不完全相同，但都摸到了紅球和黃球，摸之前不確定是哪種結果，但結果只有2 種，不是紅球，就是黃球。這樣的交流與碰撞可以讓學生的思考不僅僅停留在數據表面，而是對可能性、確定和不確定性有更深入的認識。

二、數學工具在課堂教學中的實踐應用

（一）合理使用實物工具，積累數學經驗

在小學數學學習中，使用的實物工具有很多，如小棒、圖形紙片、計數器、七巧板、釘子板等。學生合理使用這些數學工具，可以在觀察與操作實踐中積累數學經驗。“紙上得來終覺淺，絕知此事要躬行”。學生通過使用實物工具進行操作實驗，通過參與操作活動獲得感性的經驗，把操作經驗內化為數學經驗，能夠為思維發展助力。

以蘇教版數學四年級（下冊）“三角形的內角和”為例，三角形的三個角并不靠在一起，學生無法直接感知三角形內角和的大小。為此，教師可提供量角器和多張三角形紙片，讓學生動手試一試。學生既可以使用量角器測量算出三角形內角和，又可以用三角形紙片動手撕一撕、拼一拼、折一折。學生在操作實踐中發現一個三角形的三個內角合在一起能夠形成一個平角，從而發現三角形的內角和是180°。

又如，在蘇教版數學二年級（上冊）“認識線段”的教學中，教師給學生展示一根毛線，同時問道：“誰能把它拉直？”在學生拉直之后，教師適時追問：“誰能來指一指，說說從哪兒到哪兒是直的。”在學生指過之后，教師揭示線段的定義：“像這樣把線拉直，兩手之間的一段可以看作線段。”學生利用實物工具，通過觀察、動手操作，抽象出線段的定義，初步了解了線段的本質特征，在腦海中形成了線段的表象。接著，教師可以讓學生同桌合作，一人拉直毛線，一人指一指，說一說從哪兒到哪兒可以看成一條線段，豐富學生對線段的認知。此外，教師還可讓學生調整毛線的位置，變化毛線的長度與方向，讓學生發現雖然它們方向不同、長短不一，但都是直的，有兩個端點，都是線段。學生通過動手操作學具，在實踐中能夠發現各種不同線段的表現形式，總結出線段的本質特征。

（二）創意使用自制工具，適應學生需要

自制工具是指為了適應課堂教學的實際需要，針對課堂教學內容開發的感知材料，如實物、模型、儀器等器具。將自制教具應用于數學教學中，一方面可以彌補現有實物工具存在的不足，另一方面也可以激發學生的學習興趣，提高教學質量。

例如，在蘇教版數學四年級（下冊）“三角形的三邊關系”教學中，筆者發現教材中提供的4 根小棒長度是2 厘米、4 厘米、5 厘米和8 厘米，教材中沒有展示2 根小棒的長度之和與第3 根小棒長度相等時不能圍成三角形的實踐過程，而是直接明確這種情況不能圍成三角形。教師如果給學生提供兩根小棒的長度之和等于第三根這樣的學具會出現什么樣的情況呢？于是，在教學中，筆者給學生提供長度為2 厘米、5 厘米、6 厘米和8 厘米這4 根小棒，讓學生嘗試用這4根小棒去圍三角形。學生在嘗試用2 厘米、6 厘米和8厘米小棒圍三角形這種情況時，由于在實際操作中，小棒會有一定的寬度，在表象上讓這三根小棒圍成一個非常“扁”的三角形（如圖1）。這時學生會形成思維上的誤區，疑惑兩邊之和等于第三邊時是否能圍成三角形。為解決學生這一疑惑，教師可以讓學生在辯論與交流中發現是由于小棒存在寬度，如果忽略小棒的寬度，就無法圍成三角形。利用學具進行操作難道就真的無法驗證兩邊之和等于第三邊這種情況嗎？為了突破這一教學難點，筆者考慮自制學具。小棒的寬度會影響結果的判斷，那就在學具制作中克服這一不利因素，但考慮在現實中存在的物體無論長短，都會有寬度這一要素，所以在自制數學工具時，筆者考慮使用塑料軟尺，裁剪出對應長度的尺子，在操作實踐前給學生示范，把尺子帶刻度的邊靠在一起，嘗試去圍三角形（如圖2），這樣就不會受到小棒寬度這一不相關因素的干擾。

圖1

圖2

（三）靈活使用思維工具，讓認知結構化

思維工具是指對思維過程和思維結果進行可視化呈現，用圖式、思維導圖等形式將抽象的數學知識具象化，加深學生對數學知識的理解與認識，幫助學生降低理解的難度，最大程度促進學生積極探索，幫助學生建立更完善的認知結構。

以蘇教版數學四年級（上冊）“角的分類”為例，學生利用活動角不斷轉動，認識了銳角、直角、鈍角、平角和周角。然后，學生就認識的角進行分類并探討它們之間的關系，逐步形成這樣的知識結構，即銳角＜直角＜鈍角＜平角＜周角。這時，學生會產生疑惑，如比周角小又比平角大的角叫什么角？181°的角是什么角等。在討論交流中，學生嘗試利用數軸表示我們所認識的角（如圖3），逐步清晰認識到直角、平角和周角表示的是確定度數的角，而銳角和鈍角表示的是一個角的范圍。筆者可進一步給學生介紹，在大于180°、小于360°這個范圍內的角可以稱為優角，與優角相對的大于0°、小于180°這個范圍內的角被統稱為劣角。

圖3

（四）科學使用信息工具，豐富學生想象力

現代信息工具的使用為學生的數學學習帶來了許多便利。常見的數學信息工具是幾何畫板。使用幾何畫板有助于培養學生思維的敏捷性的同時，培養其發現問題、分析問題、解決問題的能力。教師利用幾何畫板動態展示教學內容或數學問題，可以把抽象的數學知識變得形象、直觀。保持幾何關系是幾何畫板的精髓和特點，幾何圖形無論如何變化，它們之間的幾何關系都保持不變。

以蘇教版數學六年級（下冊）“圓柱和圓錐”為例，有些練習是關于平面圖形怎樣旋轉形成立體圖形。但在教學設計的過程中，筆者發現學生理解起來比較困難，特別是比較復雜的圖形，曾經也嘗試過制作教具，但發現制作教具比較費時間，效果也不理想，PPT也很難實現演示的效果。而幾何畫板能有效解決這一問題，達到良好的直觀演示效果。在練習中，對于“長方形繞一條邊旋轉一周會形成什么圖形”這一問題，學生在嘗試用語言描述后用幾何畫板直觀進行演示（如圖4），對由面到體的過程形成了一個直觀的認識。通過幾何畫板還可以讓學生感受直角三角形繞兩條直角邊怎樣形成一個圓錐。幾何畫板的運用不僅僅局限在圓柱和圓錐的學習，還可以演示三角形三個內角度數不斷變化，內角和永遠等于180°（如圖5），三角形的第三條邊變化的范圍（如圖6）。

圖4

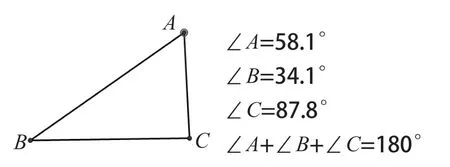
圖5

圖6

結 語

綜上所述，在小學數學教學中使用數學工具可以讓學生通過自主、合作、探究親身經歷知識發生的過程，使學生的學習過程可視化。這樣的過程可以激發學生的學習興趣，幫助他們在活動中積累經驗，形成清晰的認知結構，豐富想象力，培養思維能力和解決問題的能力，促進其數學學科核心素養的提升。同時，教師應注意，不同類型的數學工具并不是孤立的，而是相互聯系、密不可分的。教師應基于學生的學習需要，在教學過程中協同使用多種數學工具，使學生成為主動的學習者與探索者，推動學生思維品質的提升。