基于改進遺傳蜂群算法的武器系統優化部署問題研究

岳韶華，何 晟，王 剛，劉 偉，陳 晨

(1.空軍工程大學 防空反導學院， 西安 710051； 2.空軍工程大學 研究生院， 西安 710051； 3.中國人民解放軍63768部隊， 西安 710600； 4.西安衛星測控中心， 西安 710043)

1 引言

彈道導彈突擊已成為現代戰爭中實施遠程精確打擊的重要手段，具有速度快、威力大、打擊精度高、突防能力強等特點，給現代防空帶來了前所未有的挑戰，促使區域防空向大區域防空轉變。針對我方重點保衛目標區域、特定的來襲方向以及特定的來襲目標相關參數，對武器系統進行合理的配置和優化部署，制定科學合理、安全高效的優化部署策略，一直是該領域關注的重要課題，將直接影響作戰效能，具有重要的現實意義和緊迫的軍事需求。

本文在某想定背景下，將發射弧段、攔截弧段作為主要部署依據，首先根據數形結合理論，建立目標攔截能力計算模型[1]，計算出每個武器系統針對不同來襲目標的攔截能力。在此基礎上綜合考慮武器系統的攔截過程、殺傷空域，對子目標進行加權分析，得到了整體攔截能力優化模型，再采用改進遺傳蜂群算法進行分析，得到了考慮對各個目標保衛能力相對均衡性的合理可靠的優化部署方案。

2 武器系統優化部署模型基本概念

在實際戰場環境中，發射弧段和攔截弧段是衡量武器系統攔截能力的重要指標，目標在該弧段上飛行的時間越長，戰勤人員的操作空間越大，攔截成功率也越高。發射弧段、攔截弧段與反導武器系統的部署位置、探測跟蹤能力、雷達扇區角度、攔截彈飛行速度以及殺傷空域等密切關聯，以此可以設定武器系統的攔截模型[2]。將該模型得到的結果與想定的來襲彈道導彈運動參數信息相結合，可以得到武器系統對來襲目標的攔截能力評估模型。在盡可能提升整體攔截能力的同時，還需要考慮保衛各個目標的能力相對均衡，即部署位置的選擇要讓武器系統對來襲目標的攔截窗口盡可能大、縱深盡可能長且對每個來襲方向攔截能力盡可能均衡[3]。需合考慮整體攔截能力最大和均勻部署，構成武器系統部署目標函數，在此基礎上，利用改進的遺傳蜂群遺傳算法對其中變量進行尋優處理，在預先堪選陣地位置中，尋求最優部署配置方案。

當選擇某種配置部署方案后，各武器系統部署位置、雷達法線方向、對來襲目標的攔截弧長、發射弧長及發射攔截過程可確定，能計算得到該武器部署距離縱深、雷達法線方向偏離度和武器系統部署均勻度[4]。結合實際情況，在選取部署方案時主要根據整體攔截窗口與火力分布均勻性，因此本模型選取距離縱深、雷達法線方向偏離度與武器系統部署均勻度作為3個主要屬性值。

武器系統部署距離縱深指武器系統針對來襲目標來襲方向，且對目標形成攔截能力的保衛目標—遠界距離與保衛目標—近界距離之差。雷達法線方向偏離度指武器系統的雷達法線方向相對于目標來襲方向的夾角。武器系統部署均勻度為基于來襲目標在來襲方向上穿過所有武器系統殺傷區航跡長度構建的武器系統部署均勻性指標。

3 武器系統優化部署模型

對于具有n個決策變量，m個目標變量的多目標優化問題，可描述為

max(min)f(x)=(f1(x),f2(x),…,fm(x))

s.t.gi(x)≤0,i=1,2,…,G

hi(x)=0,j=1,2,…,H

(1)

式中:x為n維決策變量；f(x)為m維目標矢量，是由決策空間向目標空間映射的函數；gi(x)≤0,i=1,2,…,G定義了G個不等式約束；hi(x)=0,j=1,2,…,H定義了H個等式約束，由所有可行解組成的集合，記為Xi。

基于選取的武器系統部署距離縱深、雷達法線方向偏離度與武器系統部署均勻度作為3個主要屬性值，建立的綜合評估模型的目標函數如下：

(2)

式中：F為部署方案的綜合目標函數，F值越小，則說明該方案越優；F1、F2、F3分別為子目標函數距離縱深f1與雷達法線方向偏離度f2以及武器系統部署均勻度f3進行歸一化處理之后的結果，在后續論述中將對上述具體計算方法進行深入討論；ω1、ω2、ω3分別為縱深、雷達法線方向偏離度與均勻性相對應的權重，ω1,ω2,ω3∈(0,1)且ω1+ω2+ω3=1。

3.1 武器系統部署距離縱深

用下式所示的目標函數描述武器部署區域的縱深性。

(3)

距離區間的長度由范數‖·‖表示。Zθi越大，表示武器系統在θi方向上的縱深越大。

3.2 雷達法線方向偏離度

武器系統應盡可能早的探測到來襲目標，并對其進行穩定跟蹤，適時攔截。針對上述問題需求分析，建立雷達法線方向偏離度目標函數。

(4)

3.3 武器系統部署均勻度

為了防止在某方向上由于武器系統部署位置產生的火力盲區，造成敵來襲目標突破我方防御。第i個目標在θi方向上通過殺傷區的航跡總和記為dθi。構造描述武器系統部署均勻度的函數為

(5)

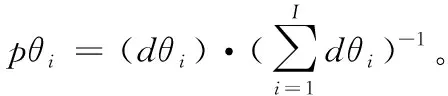
3.4 子目標函數的歸一化方法

在得到距離縱深f1與雷達法線方向偏離度f2以及均勻度f3后，由于三者量綱、數量級均不同，無法對其直接進行加權求和計算，因此，需要對其進行歸一化處理得到子目標函數F1、F2和F3，其歸一化方法如下。

對于效益型指標：

(6)

其中，l指距離縱深、雷達法線方向偏離度以及均勻性，n為方案編號。效益型指標為數值越大，綜合評估結果越好。

3.5 優化調整部署的約束條件

據建立的基于多目標組合優化理論的部署方案綜合評估模型，在求解時還需要設置相應的約束條件，其對應為求解算法中的適應度函數[5]。部分約束條件在上文已經設置，本小節對剩余關鍵約束條件進行設定并表示。

1) 權重約束。綜合目標函數中子目標函數F1、F2和F3的權重ω1、ω2、ω3滿足：ω1,ω2,ω3∈(0,1)且ω1+ω2+ω3=1。

綜上所述，所建立的基于多目標組合優化理論的部署方案綜合評估模型[6-11]為

(7)

4 改進遺傳蜂群算法

4.1 人工蜂群算法

Karaboga[12]受啟發于蜜蜂的覓食行為，于2005年提出了一種模擬蜜蜂群體尋找食物源行為的智能優化算法——人工蜂群算法(artificial bee colony algorithm，ABCA)。傳統的人工蜂群算法搜索最佳食物源的流程可以總結為4個階段[13]：

1) 初始階段。每個食物源均代表待解決問題的一個可行解，雇傭蜂數量等于跟隨蜂數量。假設搜索問題為求最小值，初始階段隨機生成SN個食物源，可以表示為

Xi, j=Xmin, j+rand(0,1)(Xmax, j-Xmin, j)

(8)

其中，i=1,2,…,SN,j=1,2,…,D，D是食物源位置變量的數量，即問題的維數，Xmin, j、Xmax, j分別是是食物源第j維的下界和上界。

2) 雇傭蜂階段。每個雇傭蜂僅對應一個食物源，因此在這個階段雇傭蜂與食物源的數量相等。每只雇傭蜂在其對應食物源Xi附近搜索，隨機選擇第j維進行更新，尋找新的食物源Vi：

Vi, j=Xi, j+φi, j(Xi, j-Xk, j)

(9)

其中，φi, j是[-1,1]之間的隨機數，k∈{1,2,…,SN}(k≠i)是隨機選擇的一個食物源,j∈{1,2,…,D}是隨機選擇的一個維度。此時，若新的食物源f(Vi)的函數值f(Vi)優于f(Xi)，就將Xi替換為Vi，否則保持Xi不變。

3) 跟隨蜂階段。當所有的雇傭蜂搜索完畢之后，跟隨蜂將收到雇傭蜂共享的食物源信息。跟隨蜂收到信息后，按照一定的概率選擇食物源進行采蜜，選擇第i個食物源的概率為

(10)

其中，fiti是食物源Xi的收益度，SN為食物源、雇傭蜂及跟隨蜂數量。

4) 偵察蜂階段。若某個食物源經過連續多次搜索后仍然沒有得到更新，則放棄此食物源，該食物源的雇傭蜂變成偵察蜂，依據式(8)進行初始化搜索，尋找新的食物源。設定搜索閾值limit，即當搜索次數超過limit時，放棄食物源。

人工蜂群算法具有搜索能力強、結構簡單、參數較少等優點，但同時也存在著收斂速度較慢、易早熟、局部搜索能力差和蜂群多樣性小等缺點。因此，引入傳統遺傳算法中的遺傳變異交叉等思想，并結合改進的自適應策略，提出一種改進的遺傳蜂群算法。該算法可以融合遺傳算法中的遺傳進化策略與蜂群算法尋優策略。充分利用二者的優勢并對缺點進行互補，具有快速、準確的全局尋優能力。

4.2 遺傳算法與蜂群算法的融合

遺傳算法(genetic algorithm，GA)是在1975年由美國的Holland教授首次提出的一種基于達爾文進化論中的自然選擇和遺傳機制的全局優化搜索智能算法，具有選擇、交叉、變異3個基本算子[14]。

在人工蜂群算法中，為了提升算法的開發能力，提高收斂速度，可以引入遺傳算法中的交叉和變異操作。

交叉操作可以使食物源集合中的2個食物源路徑之間經過交叉產生新的食物源路徑，從而獲得2個新的食物源，引導蜂群向最優食物源方向搜索進化，最終得到由全部最優的食物源組成的食物源集合。本文使用后續交叉方法，對于2條搜索路徑隨機產生一個變異點，將該變異點后續的路徑進行完全交叉。

變異操作可以增加食物源的多樣性，防止蜂群陷入局部最優解中。本文使用中間變異方法，在搜索最優路徑時，隨機產生2個隔層變異點，將2個變異點之間的路徑進行同層隨機選取。

在算法中，可以設定交叉概率參數與變異概率參數，表示交叉操作與變異操作發生的可能性，分別用Pc和Pm表示。如果變異操作過多，將影響整個蜂群搜索最優食物源的過程，因此一般情況下變異概率Pm取值較小。

4.3 食物源的自適應選擇策略

在利用智能算法解決尋優問題時，一般情況下都希望算法在初期可以更加側重于探索(Exploration)，即更多的在解空間中搜索新解，實現全局搜索，而后期則更加側重于開發(Exploitation)，即能夠在解空間中最優解附近進行更加深入的局部搜索，達到加快收斂速度的目的。為了加強算法的開發能力，可以將遺傳算法與蜂群算法進行融合，此時在遺傳蜂群算法中引入食物源的自適應選擇策略，加入自適應因子ω，讓算法可以在探索與開發之間達到平衡。自適應因子ω與算法的迭代次數有關，其表達式如下：

(11)

其中，iter為當前迭代次數，iter_max為最大迭代次數。算法在進行交叉操作時，將父代設置為跟隨蜂所在食物源與當前食物源集合中的全局最優解或該食物源的局部最優解，進行交叉操作。這樣既可局部最優問題在初期就對算法的后續進行產生影響，還可以加快算法后期搜索全局最優解的速率，最終實現提升算法整體性能的目的。

4.4 算法流程

在基本人工蜂群算法的基礎上，引入遺傳算法中的交叉操作與變異操作[15]，并結合改進的食物源自適應選擇策略，使得算法實現探索與開發的平衡，能夠做到初期全局尋優與后期快速收斂，得到了改進遺傳蜂群算法(improved genetic bee colony algorithm，IGBCA)。

利用自適應選擇策略的遺傳蜂群算法求解最優部署方案時，每一種部署方案都是一個食物源，所有的方案構成了食物源集合，通過交叉變異操作，結合自適應搜尋，可以求得收益度最高的方案路徑，該路徑即為求解得到的最優方案。

改進后的遺傳蜂群推理算法的具體步驟如下：

Step 1：初始化蜜蜂種群，雇傭蜂和跟隨蜂數量均為SN，搜索閾值limit，初始迭代次數iter=0，最大迭代次數iter_max，交叉概率Pc，變異概率Pm，此時取變異概率Pm值較小,改進的自適應因子ω=iter/iter_max；

Step 2：依據式(8)隨機產生SN個初始食物源Xi，即隨機產生SN條初始推理路徑，并計算每個食物源的收益度；

Step 3：雇傭蜂依據式(9)在食物源附近搜索新食物源Vi，計算其收益度；

Step 4：比較新舊食物源的收益度，若Vi收益度較高則替換掉Xi，否則保留Xi；

Step 5：依據式(10)計算跟隨蜂選擇食物源的概率Pi；

Step 6：跟隨蜂依據概率Pi選擇食物源；

Step 7：跟隨蜂搜索新的食物源Vi：如果Pm<φ1Pc，則進行變異操作。當進行交叉操作時，如果φ2<ω，則選擇當前食物源集合中的全局最優解作為父代；如果φ2>ω，則選擇該食物源的局部最優解作為父代。其中，φ1、φ2為[-1,1]之間的隨機數。計算新食物源的收益度；

Step 8：與Step 4相同；

Step 9：判斷某食物源的搜索次數是否超過了搜索閾值limit，若有，則依據式(9)產生新的食物源替換掉它；

Step 10：判斷是否滿足循環終止條件，即iter>iter_max，如果滿足條件則輸出當前的最優解，即最終推理路徑，否則返回Step 3，且iter+1。

5 仿真實驗結果與分析

本文采用的改進遺傳蜂群算法的目標函數由武器系統部署距離縱深、雷達法線方向偏離度和武器系統部署均勻度共同組成。在實際情況中，通過查閱資料[16-17]，本文對ω1、ω2分配0.5、0.1的權重，與此同時ω3=0.4。

實驗平臺操作系統為Windows 10，CPU型號為Intel Core i7-8750H，GPU型號為NVIDIA GTX1070。算法數據來源于某想定給定數據，其中包括基于北天東坐標的前期預選部署陣地坐標500個，來襲目標軌跡數據6組，保衛要地坐標5個。

將本文算法與蜂群算法及遺傳蜂群算法在同等時間和環境限制下的優化效果列表，如表1。

表1 算法迭代效率對比Table 1 Algorithmic iteration efficiency comparison

對算法進行性能對比，對3種算法設置相同的初始函數值和迭代次數，在迭代次數相同時，本文算法的收斂速度更快，收斂性更好。

最后在Windows操作系統環境下，基于某部署系統，進行了本文算法的實現，并對算法的效果進行了可視化，系統基本操作界面如圖1所示。

圖1 部署系統基本操作界面Fig.1 Simulation environment interface

使用本文給出的算法對某想定進行部署后，以探測面積和火力面積覆蓋為參數，分別以一層覆蓋、兩層覆蓋、要地覆蓋層數列表如表2所示。由表2可得出結論：本文算法完全達到目標要求的覆蓋條件。

表2 算法部署資源參數對比Table 2 Algorithm deployment comparison

系統得到的部署如圖2所示。其中，區域為作戰區域，白色扇形區域為武器系統雷達掃描扇區，陰影區域外線為我方保衛要地生死線，淡藍色路徑為敵方攻擊路徑。

圖2 武器系統部署示意圖Fig.2 Schematic diagram of weapon system deployment

為了更加直觀地實現武器系統部署方案的攔截效果，系統對武器系統目標探測能力和武器系統攔截能力都進行了三維可視化處理，其中目標探測跟蹤能力為綠色區域如圖3所示，攔截能力為紅色區域如圖4所示。

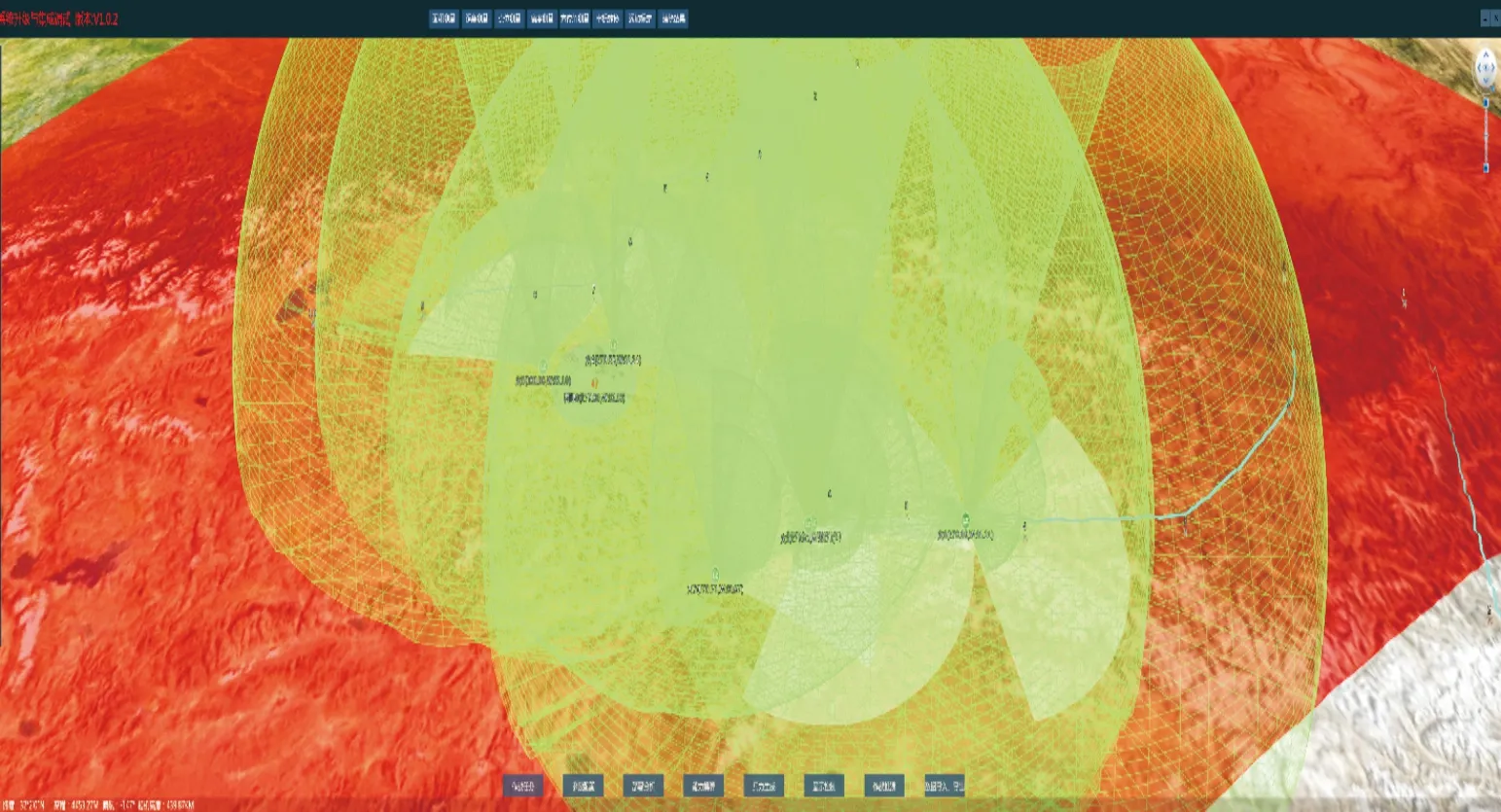
圖3 武器系統目標探測跟蹤能力三維示意圖Fig.3 3D schematic diagram of weapon system target tracking capability

圖4 武器系統攔截能力三維示意圖Fig.4 3D schematic diagram of weapon system interception capability

6 結論

本文研究了在分布環境下的武器系統優化部署問題，通過融合遺傳算法與蜂群算法的優勢，增加自適應因子，克服了傳統算法效率較低與容易陷入局部最優的缺點。基于上述改進提出了一種改進遺傳蜂群算法，設計了相關數學模型，通過分析迭代次數和目標函數值的關系以及算法最終形成的探測面積火力覆蓋面積比例，驗證了本文改進遺傳蜂群算法在武器系統優化部署時具有更加優秀的收斂性和效率，可以更加迅速達到目標要求函數值。

此外，將算法應用于指控仿真軟件時，直觀展示了基于該算法進行武器系統部署的性能，也暴露出了算法未充分考慮地形因素對武器系統探測、攔截性能影響的缺點，今后將針對該問題進一步研究。