D字異型彈體斜侵徹多層鋼靶彈道研究

胡雪垚，屈可朋，肖 瑋

(西安近代化學研究所， 西安 710065)

1 引言

侵徹彈是打擊深層地下工事、大型水面艦艇等多層目標的重要手段。隨著異構型高速遠程打擊飛行器等武器平臺的快速發展，研制與其共形的戰斗部結構，以增強武器彈藥毀傷威力，已成為國內外科研人員研究的熱點。在異構型武器平臺特定的幾何空間內，戰斗部一方面要滿足武器平臺的空間幾何尺寸及飛行載荷要求，更重要的是要滿足侵徹目標時的動力學要求。

目前，國內外針對非圓截面彈體侵徹特性開展了眾多研究。Partom等通過數值仿真分析了不同速度下旋轉對稱彈體和平面對稱彈體侵徹金屬靶板的過程，結果表明，在1 500 m/s速度下平面對稱彈體侵徹效率更高。隨后，Bless等通過對比異型截面彈體和圓截面彈體的高速侵徹能力發現，在臨界速度以下時，異型截面彈體的侵徹效率高于圓截面彈體。杜忠華等針對相同質量、截面積以及沖擊速度條件下，3種截面形狀(三角形、四邊形和圓形)彈體侵徹半無限靶板開展了試驗研究，發現在一定速度范圍內，3種截面形狀彈體的侵徹深度隨著速度的增大基本呈線性增加趨勢；但當速度增大至1 700 m/s以上時，異型截面彈體的侵徹能力明顯優于圓形截面彈體。王曉東等開展了不同截面形狀長桿彈侵徹半無限靶的試驗和理論研究，發現與圓截面長桿彈相比，不同異型截面長桿彈均表現出更優異的侵徹能力，且在大長徑比、高著速條件下異型截面長桿彈的優勢更加顯著。此外，在彈體頭部或者彈身刻槽也是一種常用的提高彈體侵徹能力的方法。

盡管上述典型非圓截面彈體的侵徹能力均優于傳統圓截面彈體，但由于非回轉體自身的幾何特性，彈體無法避免侵徹過程中的不對稱受力，因此，非圓截面彈體的侵徹特性會受到更多因素的影響。王文杰等發現，當彈體質量和長度一致時，橢圓截面彈體長短軸參數的改變對侵徹性能影響較為顯著。Dai等建立的理論模型進一步驗證了該結論。張永亮等發現大攻角對異型彈姿態俯仰角的影響遠大于侵徹著角的影響，且攻角的方向起著重要作用。王浩等開展了橢圓截面和橢圓變截面彈體斜侵徹兩層間隔鋼靶的試驗和仿真研究，發現兩種彈體貫穿后靶板均呈橢圓形開孔，且長軸方向對橢圓變截面彈體的偏轉規律影響較大。上述研究主要針對典型多邊形或橢圓截面彈體，而異構型武器平臺通常為上下不對稱幾何結構，目前針對上下不對稱異型彈體侵徹特性的研究較少。

本研究中設計了一種上下不對稱D字異型彈體，對其斜侵徹多層鋼靶過程進行了數值模擬和實驗驗證，分析了侵徹速度、侵徹著角、以及彈尖高度對其侵徹彈道的影響，以期為與武器平臺共形的戰斗部設計提供支撐。

2 D字異型彈體及仿真模型

2.1 D字異型彈體

參照常規侵徹彈形狀及結構，設計的D字異型縮比彈體結構如圖1所示。該異型彈體為上下不對稱異構體，彈體橫截面呈D字型。彈體總長度為140 mm，高度為44 mm，彈身上下表面寬度和分別為20 mm和60 mm，內腔長度為100 mm，內腔直徑為30 mm。彈尖高度為彈身軸線與彈頭中心點距離，初始狀態=0 mm。

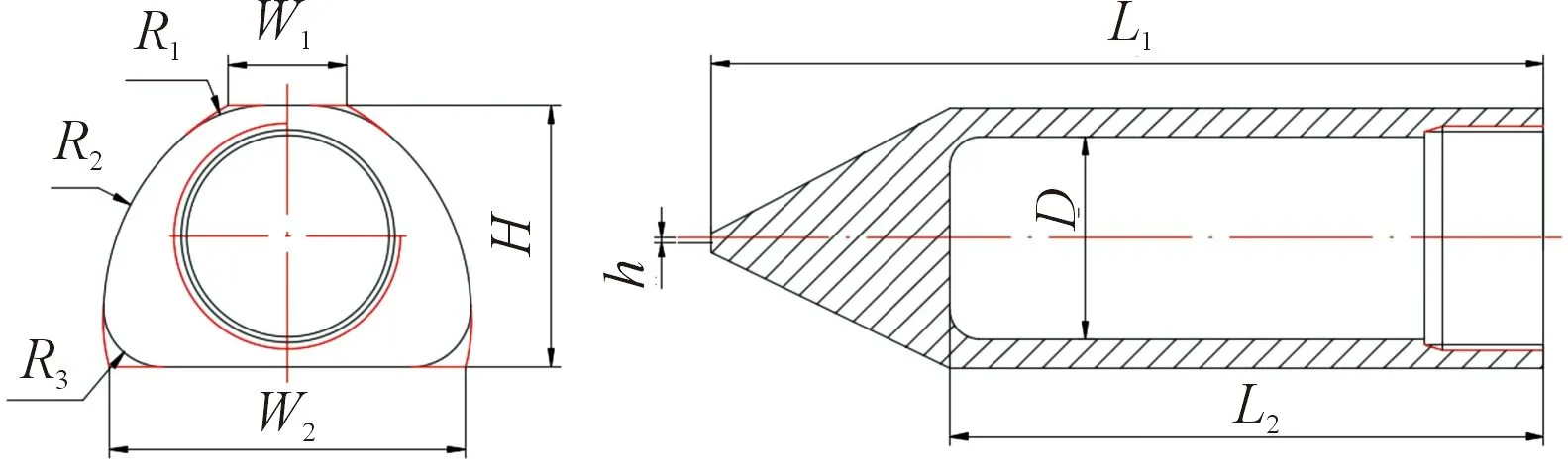
圖1 D字異型彈體結構示意圖Fig.1 Schematic of the D-shaped projectile

2.2 仿真模型

采用Hypermesh軟件建立了D字異型彈體與靶板的精細化網格模型，其中彈體包括殼體、裝藥和堵蓋3部分，具體如圖2所示。模型中侵徹著角取0°～20°，攻角0°，靶板間垂直距離為300 mm。

圖2 D字異型彈體侵徹三層間隔鋼靶有限元模型示意圖Fig.2 Finite element model of D-shaped projectile penetrating three-layered steel targets

D字異型彈體和靶板均采用拉格朗日網格，彈體與靶板之間定義侵蝕接觸(CONTACT_ERODING_SURFACE_TO_SURFACE)，裝藥與殼體之間選用面面接觸(CONTACT_AUTOMATIC_SURFACE_TO_SURFACE)算法。靶板材料選用Johnson-Cook本構模型，可綜合考慮塑性大變形、應變率以及溫度效應對材料塑性力學行為的影響，并通過Johnson-Cook失效模型描述材料的損傷特性，具體材料參數見表1所示。由于Johnson-Cook本構模型中屈服面與狀態方程是解耦的，引入Grüneisen狀態方程進行計算，該狀態方程是描述固體材料高壓狀態下的經典方程，廣泛應用于彈體侵徹的數值模擬中。彈體采用剛性模型，可在保證一定準確性的條件下大幅提高計算效率。

表1 靶板材料參數Table 1 Material parameters of target

3 仿真結果及討論

彈體斜侵徹靶板時，彈體與靶板的接觸區域將受到非對稱載荷，從而使彈體產生角速度和角加速度，易于發生彈道偏轉，加之翻轉力矩隨著彈體侵入深度呈現非線性變化，當彈體出靶后彈道將發生明顯變化。通常認為這一過程受彈體結構、侵徹速度、靶標材質、著角、攻角等諸多因素的影響。本文中設計的D字異型彈體為非對稱結構，自身幾何外形的非對稱性將加劇穿靶過程中載荷分布的不均衡，導致侵徹彈道偏轉規律更為復雜。本研究在靶標材質、攻角等因素不變的條件下，著重討論侵徹速度、侵徹著角以及彈尖高度對其侵徹彈道的影響規律。

3.1 侵徹著角、侵徹速度對彈道的影響

圖3給出了400～800 m/s侵徹速度下，D字異型彈體以不同著角侵徹三層間隔鋼靶的彈道偏轉曲線。在400 m/s速度下[如圖3(a)所示]，不同著角彈體的侵徹軌跡均為向下偏移，彈體總偏移量隨侵徹著角的增大分別增加154.5%和367.2%。當侵徹速度增大至600 m/s以上時[如圖3(b)和圖3(c)所示]，隨侵徹著角增大，彈體運動軌跡由向下偏轉逐漸轉變為向上偏轉，且800 m/s時彈體最終運動方向與水平方向的夾角呈增大趨勢。

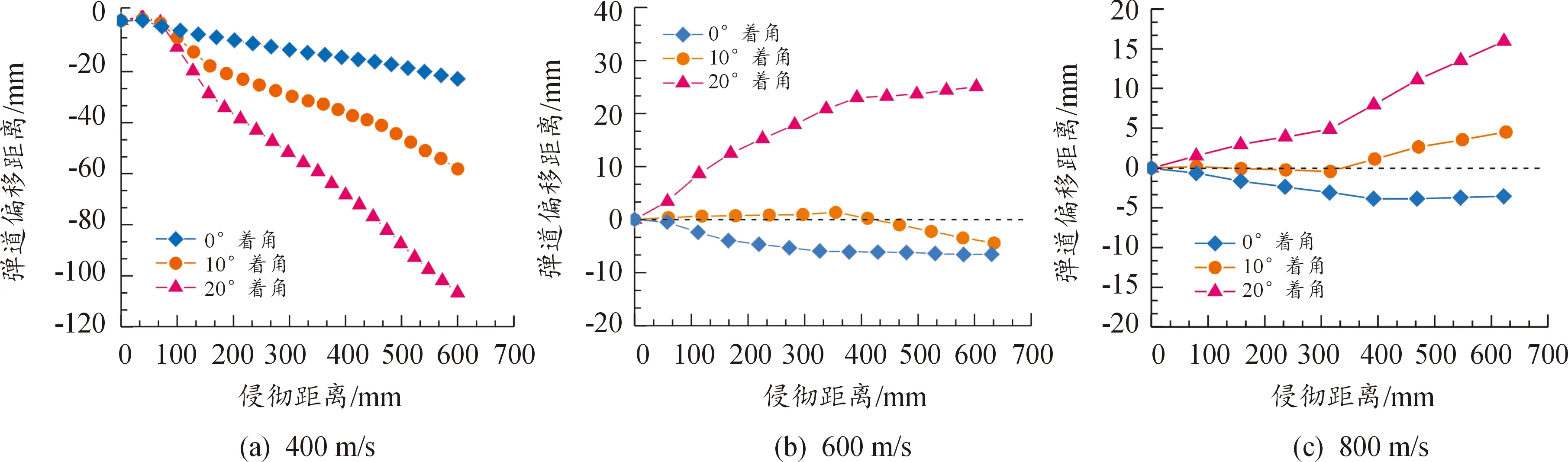
圖3 不同著角下彈道偏移距離曲線Fig.3 Comparison of trajectory deflection at different impact angles

圖4顯示了不同著角、不同速度條件下，彈道總偏移量的變化趨勢。結果表明，隨侵徹著角的增大，不同速度彈體的侵徹總偏移量基本呈遞增趨勢[見圖4(a)]；而隨著侵徹速度的增大，盡管彈體的彈道偏轉方向可能不同，但其彈道穩定性呈提升趨勢，即彈道總偏移距離的絕對值減小[見圖4(b)]。其中，10°著角條件下侵徹速度對彈道穩定性的影響最為顯著，由400 m/s增加至600 m/s時，彈道總偏移量減小94%。

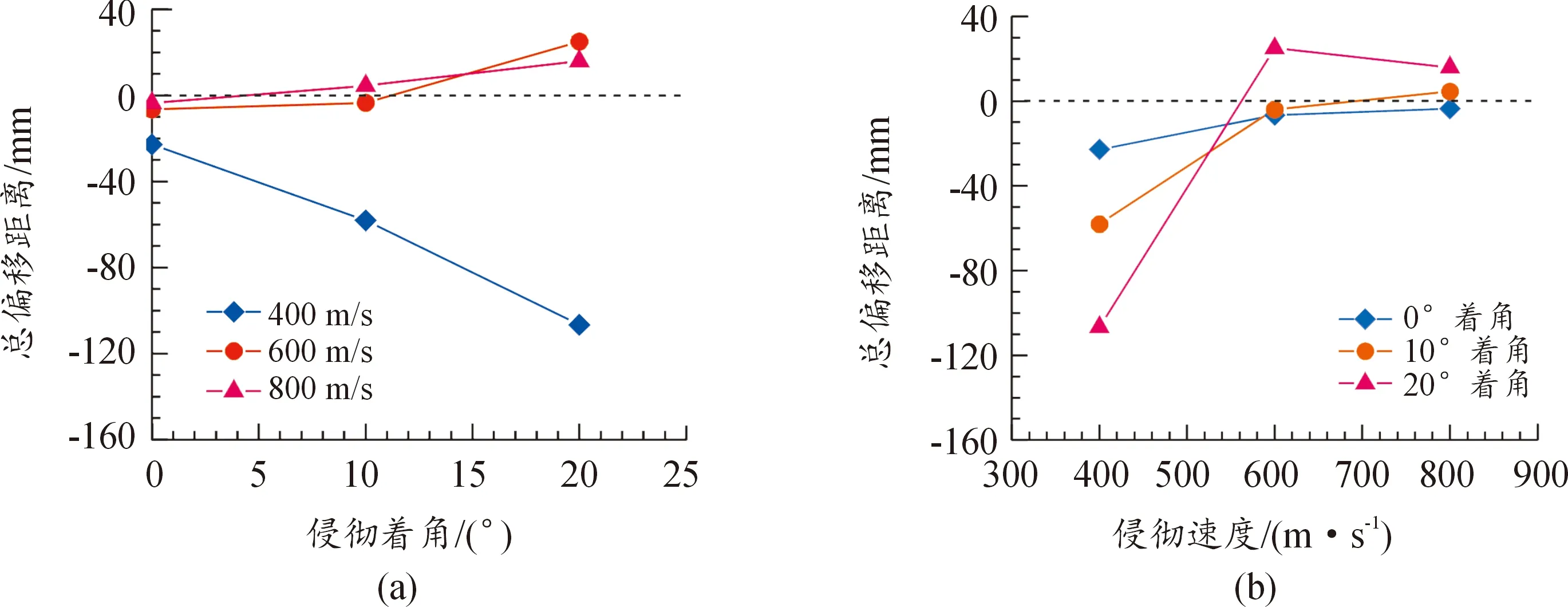
圖4 彈道總偏移距離變化曲線Fig.4 Variation curves of total trajectory deflection

彈體截面形狀是影響其侵徹過程中受力分布的重要因素之一，圖5為D字異型彈體沿橫截面內的受力示意圖。其中，、和分別為圓弧、和的圓心，以彈體中心為原點，軸和軸分別沿平行和垂直于彈體上下表面的方向。由于該字異型彈體關于軸對稱，若只改變著角，則沿軸方向的受力可相互抵消，僅沿軸方向的受力發生改變。

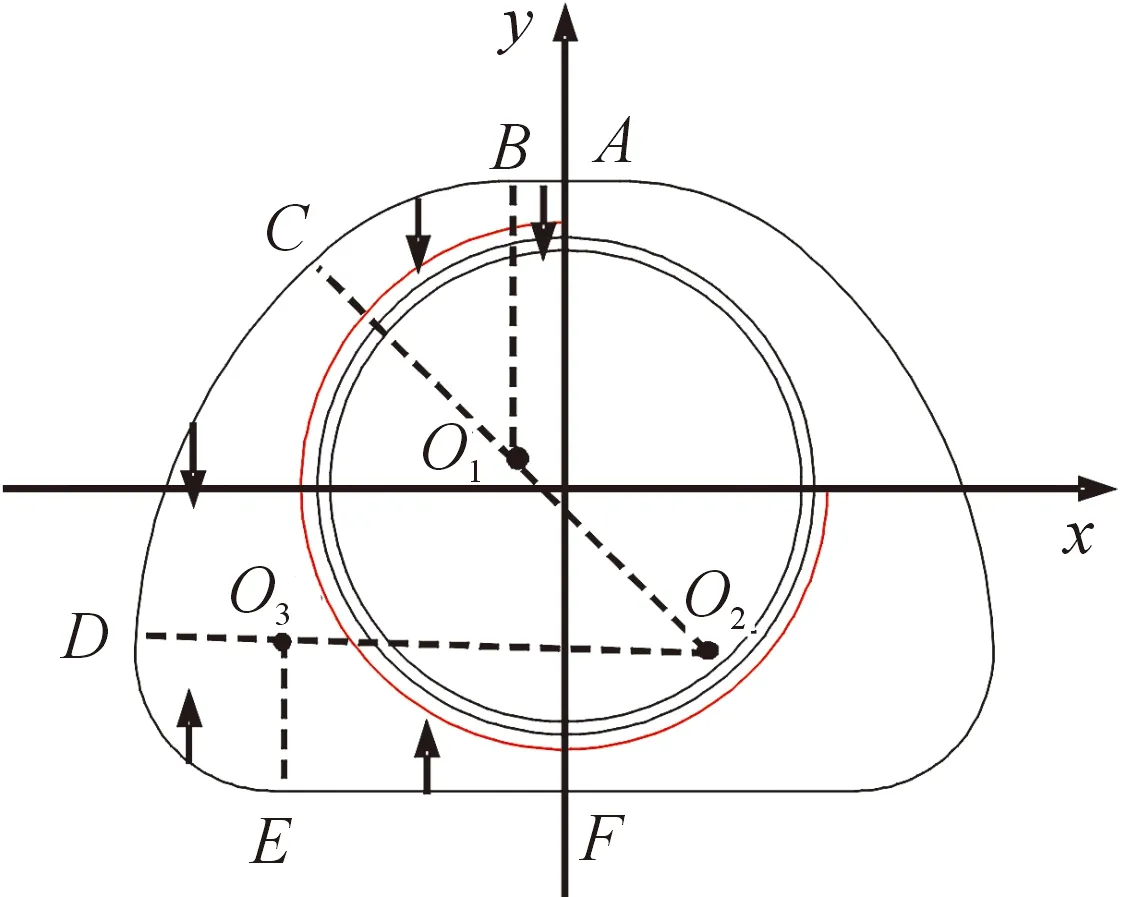
圖5 彈體截面受力示意圖Fig.5 Illustration of force distribution along the cross section of projectile

圖6為10°著角，400 m/s速度下彈體接觸力和繞軸角速度隨時間的變化曲線，其中彈體向上抬頭為正，向下低頭為負。可以看出，彈體侵徹單層靶板的過程大致可以分為頭部接觸和尾部接觸2個階段。第一階段為彈體與靶板接觸直至彈體頭部基本穿出靶板，該階段內彈體角速度先減小后迅速反向增大，彈體呈現略向上偏轉的趨勢；第二階段為彈體完全穿出靶板前，該階段內彈體的偏轉規律更加復雜，可能受到彈體實時速度、靶板的破壞模式以及接觸力的大小、方向等多重因素的影響。

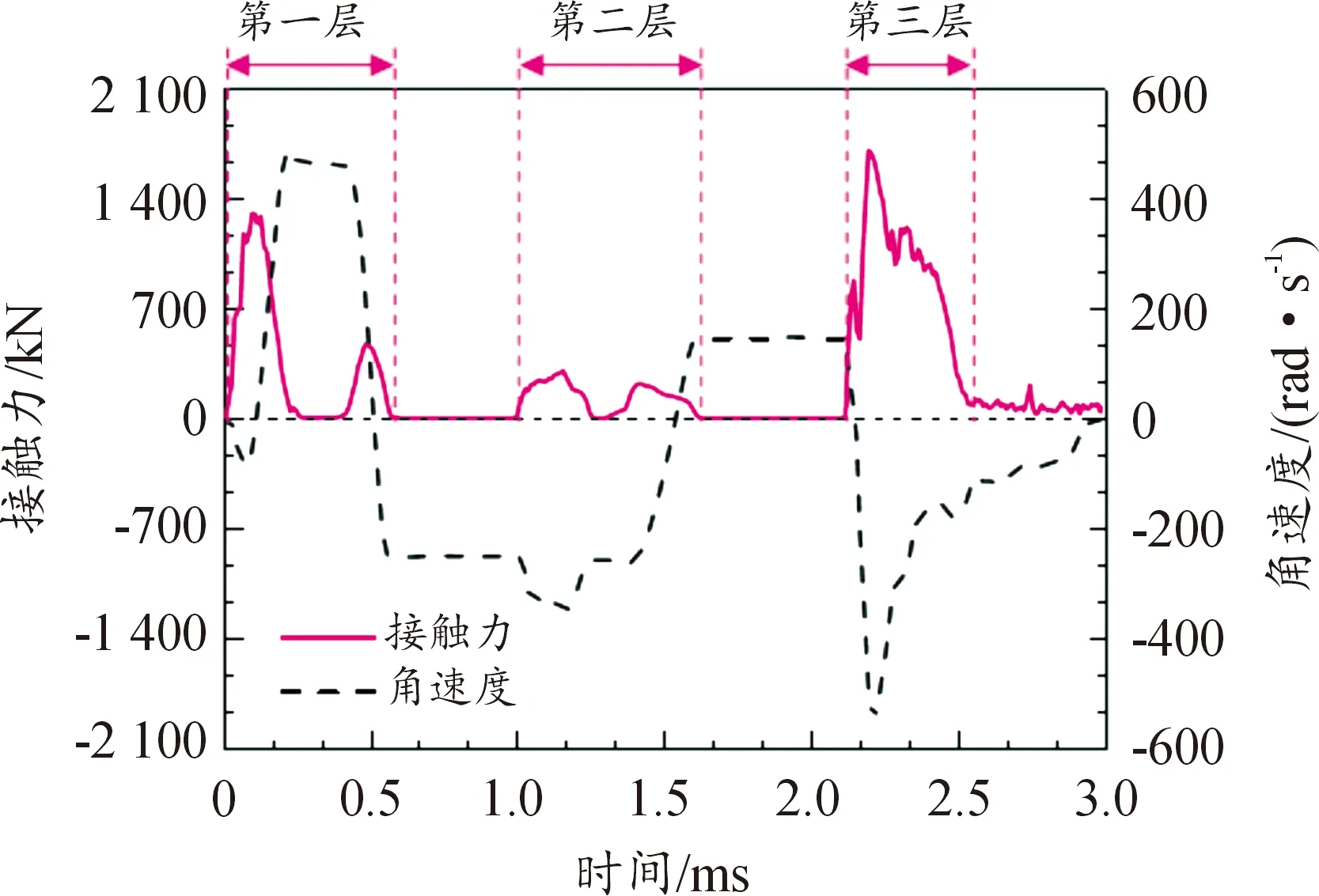
圖6 接觸力-時間曲線及角速度-時間曲線Fig.6 Contact force-time curve and angular velocity-time curve

圖7給出了400 m/s彈體侵徹第一層靶板時的彈靶接觸作用過程，可以看出，在彈體剛剛侵入靶板時，彈體運動姿態與初始狀態一致，彈體上下表面所受到的接觸力基本平衡；隨著彈體頭部繼續侵入，靶板上表面所受到的接觸力逐漸減小；當彈體頭部完全穿出靶板后的一段時間內，彈體所受接觸力為零，直至由于姿態偏轉導致彈體尾部與靶板下表面接觸，此時彈體角加速度為順時針方向。盡管彈體所受載荷是其姿態變化的決定性因素之一，但侵徹過程中的彈靶作用機制非常復雜且影響因素繁多，本文主要以規律性研究為主。

圖7 400 m/s時彈靶接觸作用過程示意圖Fig.7 Contact process during penetration at 400 m/s

3.2 彈尖高度的影響

彈體的幾何外形也是影響其彈道穩定性的重要因素，為了不改變彈體的截面形狀，本文中通過改變彈尖高度來調整彈體所受合力的大小和方向。取彈體高度方向作為方向，以彈體中心點作為零點，向上為正向下為負。分別取彈尖高度為0 mm、0.8 mm、0.9 mm、0.95 mm、1.1 mm和1.7 mm，通過數值仿真獲取彈尖高度對異型彈體侵徹彈道偏轉規律的影響，此處選取一種彈道總偏移距離較大的工況(400 m/s，10°著角)進行分析。圖8反映不同彈尖高度條件下，彈體侵徹第二和第三層靶板時的彈道偏移距離。可以看出，隨著彈尖高度的升高，彈體由向下偏轉逐漸轉變為向上偏轉，彈道偏轉距離呈現先減小后反向增大的變化趨勢，且在0.8～1.1 mm，彈道偏轉距離隨彈尖高度的變化顯著。

圖8 彈尖高度對彈道偏轉規律的影響曲線Fig.8 Effect of the height of nose tip on trajectory deflection

實際上，改變彈尖高度就是改變彈體頭部的載荷分布。當彈尖位置上移，彈體頭部上表面與靶板法向夾角減小，彈體頭部上表面受力面積及其所受載荷的法向分量sin減小(如圖9所示)，相反地，下表面受力面積及其所受載荷的法向分量增大，使得彈體由“低頭”逐漸轉變為“抬頭”。當彈體頭部所受合力方向與彈體運動方向趨于一致時，所對應的彈尖高度即為保證彈道穩定的最優解。在400 m/s速度、10°著角條件下，彈尖高度為0.95 mm時D字異型彈體的最大偏移量僅為6.7 mm，其彈道穩定性最好。

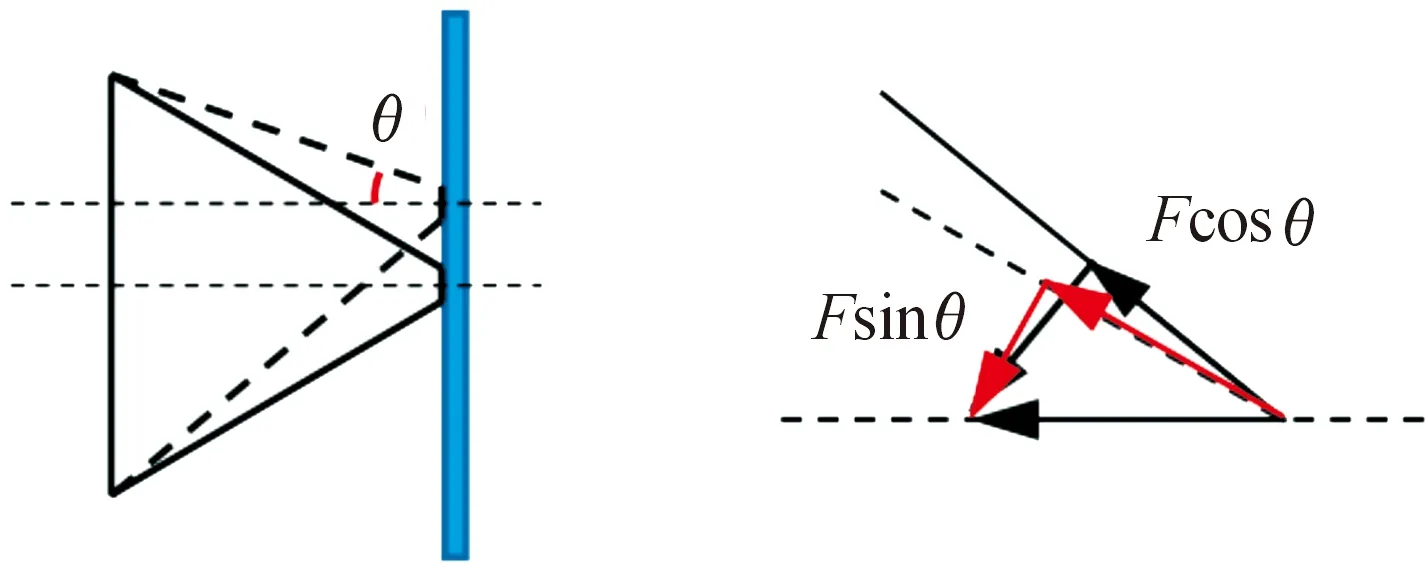
圖9 彈體頭部受力示意圖Fig.9 Illustration of force distribution ofprojectile nose

4 試驗

選用彈尖高度為0 mm的D字異型彈體進行試驗驗證，以130 mm口徑一級輕氣炮為驅動源，利用高壓氣體驅動彈體撞擊三層間隔鋼板，彈體初始速度為400 m/s，侵徹著角為10°，靶板材料為熱軋態45#鋼，試驗布局如圖10所示。

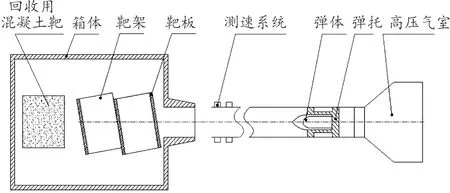
圖10 試驗布局示意圖Fig.10 Schematic of the experimental setup

圖11為試驗后三層鋼靶和彈體的宏觀損傷照片。

圖11 彈靶宏觀損傷照片Fig.11 Macroscopic damage of targets and projectile

可以看出，首層靶板的穿孔形狀與彈體橫截面基本一致，隨著靶板層數的增加開孔尺寸逐漸增大，三層靶板均呈花瓣式開裂損傷，其中第三層靶板與彈體上表面接觸的區域有明顯的撕裂損傷。且彈身上表面有輕微劃痕，劃痕區域呈放射狀，越靠近尾部磨損區域越寬[如圖11(b)所示]，彈身下表面未觀測到明顯劃痕。靶板和彈體的損傷分布表明，彈體在侵徹過程中發生了偏轉，彈軸與靶板法線的夾角隨靶板層數增加逐漸增大。通過測量試驗后靶板穿孔的位置和尺寸，可以推算出彈體侵徹過程中的彈道偏轉規律，圖12表示了彈道偏移距離和靶板背面損傷情況，結果表明，試驗結果與仿真結果吻合較好，彈道偏移距離最大誤差不超過12%。

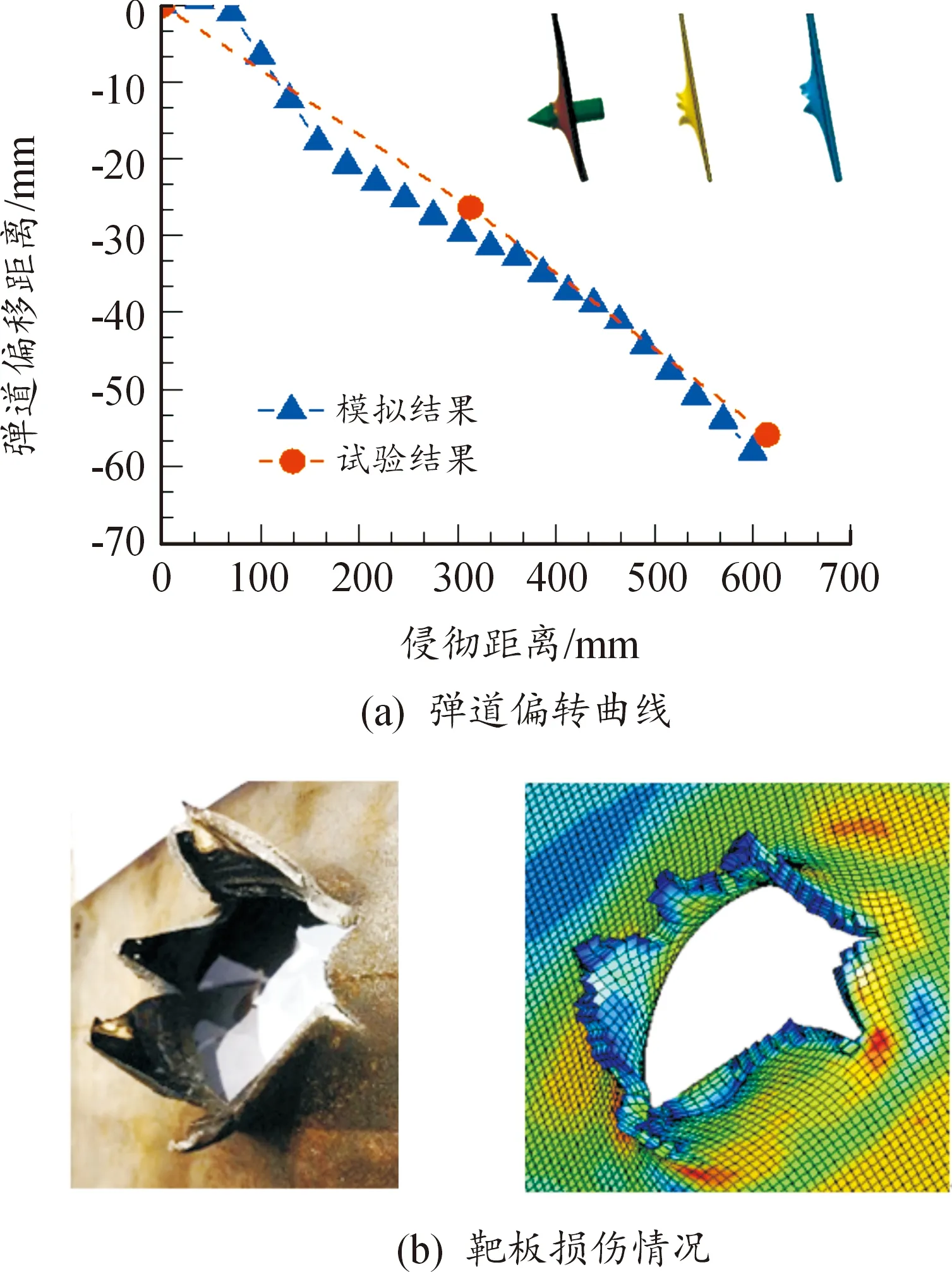
圖12 試驗和數值仿真結果Fig.12Comparisons of experimental and simulation results

5 結論

1) 隨著角增大，不同速度彈體的侵徹總偏移量呈遞增趨勢，但偏轉方向不同。其中，400 m/s時彈體偏轉最大，總偏移量分別增加154.5%和367.2%。

2) 隨速度增加，不同著角彈體總偏移距離呈遞減趨勢，彈道穩定性提升。其中10°著角條件下，侵徹速度對彈道穩定性的影響最為顯著。

3) D字異型彈體的侵徹彈道穩定性受到彈尖高度的影響，在400 m/s、10°著角下，隨彈尖高度增加彈道總偏移距離呈現先減小再反向增大的變化趨勢，且在0.95 mm時彈道穩定性最好。