基于交互多模型Kalman的無人集群跟蹤優(yōu)化算法

高文哲 李 智

(四川大學(xué)電子信息學(xué)院 四川 成都 610065)

0 引 言

我國領(lǐng)海和領(lǐng)空地域遼闊，為防止非法機(jī)動目標(biāo)闖入我國海域和空域，往往采用無人集群巡邏編隊方式[1]實(shí)現(xiàn)對海域或空域的巡視。在這種場景下，需要派出無人艇或無人機(jī)對可疑目標(biāo)進(jìn)行跟蹤。常見的跟蹤方法有視覺目標(biāo)跟蹤和電磁目標(biāo)跟蹤[2]，由于地域遼闊，調(diào)用攝像頭從視頻中定位跟蹤目標(biāo)的精度較低，并且跟蹤范圍受限，所以往往利用雷達(dá)或者電磁測距傳感器實(shí)現(xiàn)對電磁目標(biāo)的跟蹤行為。但傳感器采集的數(shù)據(jù)都攜帶噪聲干擾，這會直接導(dǎo)致目標(biāo)的實(shí)際位置與探測器的探測位置有較大的偏差，使得跟蹤行為不精確。所以在工程運(yùn)用中，無論是對雷達(dá)數(shù)據(jù)還是測距傳感器的數(shù)據(jù)都需要通過濾波方法[3]去得到與目標(biāo)真實(shí)位置較為接近的濾波數(shù)據(jù)。

卡爾曼濾波是噪聲處理的有效手段。在由觀測數(shù)據(jù)和噪聲形成的線性高斯系統(tǒng)中，常用經(jīng)典的卡爾曼濾波[4]對目標(biāo)的狀態(tài)做最優(yōu)估計，得到較好的跟蹤效果。但為滿足實(shí)際系統(tǒng)中存在的非線性模型[5]，又提出了EKF[6]和無跡卡爾曼濾波(UKF)[7]等方法。EKF主要是將非線性模型進(jìn)行泰勒展開略去二階及以上項，將一個非線性系統(tǒng)近似成線性系統(tǒng)，而UKF是對非線性系統(tǒng)中的一步預(yù)測方程使用無跡變換(UT)[8]，避免EKF引入的線性化誤差。為解決EKF算法魯棒性[9]的問題，引入了強(qiáng)跟蹤卡爾曼濾波算法(STF)[10]。而集合卡爾曼濾波[11]解決了傳統(tǒng)卡爾曼濾波計算復(fù)雜度高的問題，是對經(jīng)典卡爾曼濾波的優(yōu)化改進(jìn)。為了進(jìn)一步減小噪聲對估計值的影響，提出神經(jīng)網(wǎng)絡(luò)卡爾曼濾波[12]實(shí)現(xiàn)對噪聲統(tǒng)計特性的自適應(yīng)估計[13]。而當(dāng)目標(biāo)突然轉(zhuǎn)彎或者加、減速時，需要采用自適應(yīng)能力較強(qiáng)的濾波算法——交互多模型Kalman濾波(IMM)算法。

本文在無人集群協(xié)同作業(yè)場景下，當(dāng)出現(xiàn)可疑目標(biāo)時，集群調(diào)度系統(tǒng)需要調(diào)度當(dāng)前距離可疑目標(biāo)最近并且無其他任務(wù)的無人智能單元對目標(biāo)進(jìn)行跟蹤，同時選擇若干距離次之的無人智能單元對目標(biāo)進(jìn)行協(xié)同跟蹤，將每個無人智能單元上的電磁傳感器的輸出作為優(yōu)化算法的輸入，優(yōu)化算法通過IMM濾波對每組數(shù)據(jù)進(jìn)行濾波處理后得到若干組跟蹤目標(biāo)的狀態(tài)估計值，將這些估計值作為極大似然估計融合算法的樣本值，利用極大似然估計通過樣本值求出每個智能單元估計值的似然概率，并以似然概率作為若干智能單元的狀態(tài)估計權(quán)值，最后輸出經(jīng)過數(shù)據(jù)融合的跟蹤目標(biāo)狀態(tài)估計值，在電磁傳感器的每一個采樣周期內(nèi)都進(jìn)行一次上述過程的處理，形成最終的優(yōu)化目標(biāo)跟蹤路線。最后仿真結(jié)果展示了在無人艇群的場景下，單艇運(yùn)用IMM濾波和多艇運(yùn)用集群優(yōu)化算法，以及不同數(shù)量的多艇采用基于IMM濾波的優(yōu)化算法進(jìn)行目標(biāo)跟蹤的這兩組跟蹤路徑對比結(jié)果，以及這兩種情況下的濾波誤差均值和標(biāo)準(zhǔn)差對比結(jié)果。

1 基于IMM的無人集協(xié)同跟蹤算法

1.1 無人集群跟蹤模型架構(gòu)

無可疑目標(biāo)情況下，無人集群在各自的巡視區(qū)域內(nèi)巡邏。當(dāng)出現(xiàn)可疑目標(biāo)時，集群調(diào)度系統(tǒng)會派遣一艘暫無作業(yè)任務(wù)的無人智能單元對目標(biāo)實(shí)行跟蹤，但為加強(qiáng)跟蹤精度，本文考慮讓靠近可疑目標(biāo)的、未收到跟蹤任務(wù)的其他智能單元協(xié)同參與目標(biāo)的路線估計。在執(zhí)行跟蹤目標(biāo)的無人智能單元以及協(xié)同估計的無人智能單元數(shù)量確定后，在每個采樣周期內(nèi)調(diào)度系統(tǒng)依據(jù)其他無人智能單元與可疑目標(biāo)的距離分配協(xié)同無人智能單元，與跟蹤無人智能單元并行地從各自的傳感器搜集對可疑目標(biāo)的觀測數(shù)據(jù)，然后分別執(zhí)行IMM濾波算法得到各自對可疑目標(biāo)的估計值，通過距離坐標(biāo)轉(zhuǎn)換算法將采樣周期內(nèi)的估計值全部轉(zhuǎn)化成相對于跟蹤無人艇初始點(diǎn)的位置，再將轉(zhuǎn)化后的每組狀態(tài)估計值作為極大似然估計系統(tǒng)的輸入求出每組值得出似然估計概率，并將此似然估計概率作為每組IMM濾波輸出狀態(tài)值得到權(quán)值，通過這種交互策略求出的權(quán)值能使跟蹤無人艇的最終跟蹤路線有較好的跟蹤效果，最后通過帶權(quán)融合系統(tǒng)得到最優(yōu)的跟蹤目標(biāo)狀態(tài)估計值，執(zhí)行跟蹤任務(wù)的無人智能單元利用這個最優(yōu)值對目標(biāo)進(jìn)行可靠跟蹤，而參與協(xié)同跟蹤任務(wù)的無人智能單元的路徑不受影響。

圖1為無人集群目標(biāo)跟蹤系統(tǒng)的整體架構(gòu)。

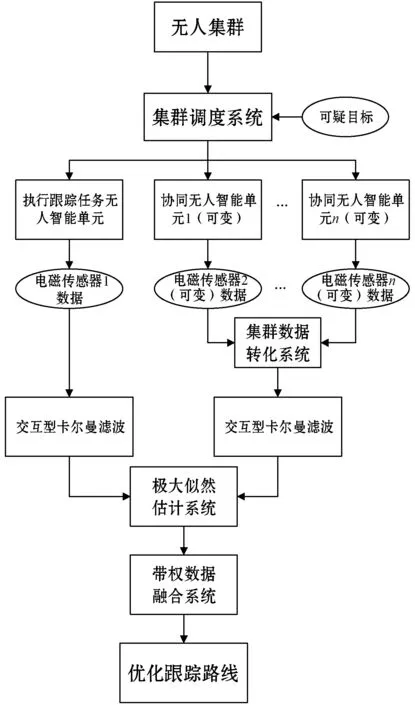
圖1 無人集群目標(biāo)跟蹤系統(tǒng)結(jié)構(gòu)

需要說明的是，為了避免當(dāng)前跟蹤任務(wù)對協(xié)同無人智能單元原任務(wù)產(chǎn)生影響，協(xié)同跟蹤只是協(xié)同無人智能單元在原巡邏路線上對目標(biāo)進(jìn)行距離坐標(biāo)數(shù)據(jù)的采集，協(xié)同無人智能單元并不是固定的。在整個跟蹤過程中，電磁傳感器在每一個采樣周期內(nèi)，都需要依據(jù)距離對協(xié)同無人智能單元的選擇進(jìn)行一次更新，所以在整個跟蹤過程中，除了最開始確定為跟蹤任務(wù)的無人智能單元不需要改變，協(xié)同無人智能單元都是依據(jù)距離不斷更新的。而不同的協(xié)同無人智能單元在采樣周期內(nèi)將所采集的數(shù)據(jù)送至集群數(shù)據(jù)轉(zhuǎn)換系統(tǒng)，經(jīng)過距離轉(zhuǎn)換算法，換算成跟蹤無人智能單元與可疑目標(biāo)的距離，然后再經(jīng)過IMM濾波處理。

1.2 交互多模型卡爾曼濾波

IMM算法雖然包含不同的模型，但這些模型中都不存在一個完全正確的模型，輸出是多個濾波器估計結(jié)果的加權(quán)平均值。權(quán)重即為該時刻模型正確描述目標(biāo)真實(shí)運(yùn)動的模型概率。

IMM算法每次遞推含四個步驟。

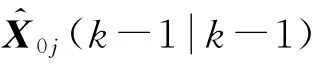
預(yù)測計算式表示為：

(1)

式中：φj表示被觀測系統(tǒng)的狀態(tài)傳遞矩陣。

預(yù)測誤差協(xié)方差計算式表示為：

(2)

式中：Gj表示系統(tǒng)擾動矩陣；Qj表示系統(tǒng)誤差的協(xié)方差矩陣。

Kalman增益計算式表示為：

Kj(k)=Pj(k|k-1)HT[HPj(k|k-1)HT]-1+

Pj(k|k-1)HTR-1

(3)

式中：H表示信道矩陣；R表示測量誤差的協(xié)方差矩陣。

狀態(tài)更新計算式表示為：

Kj(k)H(k)Xj(k|k-1)

(4)

式中：Z表示目標(biāo)觀察矩陣。

協(xié)方差矩陣更新計算式表示為：

Pj(k|k)=[I-K(k)H(k)]P(k|k-1)

(5)

步驟3模型概率更新。采用似然函數(shù)來更新模型概率μj(k)，模型j的似然函數(shù)表達(dá)式表示為：

(6)

步驟4輸出交互。對每個濾波器的估計結(jié)果加權(quán)合并，得到總的狀態(tài)估計Xj(k|k)和總的協(xié)方差估計P(k|k)。

總的狀態(tài)估計計算式表示為：

(7)

總的協(xié)方差估計計算式表示為：

(8)

1.3 多模型建模

通過分析海域[14]環(huán)境、空域環(huán)境、可疑目標(biāo)的運(yùn)動規(guī)律可知，可疑目標(biāo)一般在運(yùn)動過程中呈現(xiàn)較大的機(jī)動性和隨機(jī)性[15]，目標(biāo)在被跟蹤的過程，往往存在勻速、突然加減速和突然轉(zhuǎn)彎等情況，所以在線性系統(tǒng)的框架下，利用IMM濾波算法構(gòu)建的運(yùn)動模型應(yīng)當(dāng)包含目標(biāo)可能出現(xiàn)的所有狀態(tài)。在此基礎(chǔ)上構(gòu)建三個模型，包含一個非機(jī)動模型描述目標(biāo)的勻速運(yùn)動狀態(tài)，一個機(jī)動模型描述目標(biāo)的加速轉(zhuǎn)彎，另一個機(jī)動模型描述目標(biāo)的減速轉(zhuǎn)彎。

(1) 非機(jī)動模型。非機(jī)動模型下的物體加速度為0，同時假設(shè)非機(jī)動模型不受過程噪聲的影響，即W(k)的方差為0。可疑目標(biāo)的狀態(tài)包含x和y方向上的速度、位移和加速度。由此可以得到在非機(jī)動模型下，可疑目標(biāo)在k時刻的狀態(tài)矩陣X(k)和狀態(tài)轉(zhuǎn)移矩陣φ(k)。得到以下推斷:

(9)

式中：T表示時間。

(2) 機(jī)動模型。機(jī)動模型存在加速和減速的過程，同時假設(shè)兩個機(jī)動模型都存在過程噪聲，并且噪聲方差分別為Q1=q1I2×2、Q2=q2I2×2。

(10)

上述兩個機(jī)動模型的狀態(tài)轉(zhuǎn)移矩陣和噪聲方差分別相等，即φ2=φ3，G2=G3，則有X1(k)=X2(k)。

濾波誤差均值計算式表示為：

(11)

濾波誤差的標(biāo)準(zhǔn)差計算式表示為：

(12)

1.4 多模型建模極大似然融合算法

1.4.1極大似然估計求權(quán)值

電磁坐標(biāo)傳感器的數(shù)據(jù)采集可信度α關(guān)于跟蹤目標(biāo)與傳感器采樣時的位置之間的距離的函數(shù)，以x方向的可信度為例，距離X服從μ=0的正態(tài)分布，即N(0,σ2),其概率密度函數(shù)f(x)滿足：

(13)

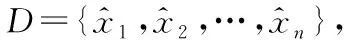
(14)

對式(14)作對數(shù)變換，得到：

(15)

對式(15)分別進(jìn)行對μ、σ2的一次偏導(dǎo)，結(jié)果如下：

(16)

(17)

聯(lián)合解得：

(18)

(19)

(20)

根據(jù)似然值可以求得任意一個無人智能單元j對跟蹤目標(biāo)的狀態(tài)估計值在這一組樣本值中所占權(quán)值wj如下：

(21)

需要指出的是，由于電磁坐標(biāo)傳感器的數(shù)據(jù)可信度與自身和跟蹤目標(biāo)的距離有關(guān)，所以坐標(biāo)傳感器對于跟蹤目標(biāo)的觀測值，在x方向與y方向有不同的可信度，權(quán)值的求解方法與上述過程一致。

1.4.2坐標(biāo)轉(zhuǎn)換

單個無人艇在進(jìn)行跟蹤目標(biāo)的過程中，主要依靠自載的距離傳感器對可疑目標(biāo)進(jìn)行數(shù)據(jù)搜集。同時，由于無人艇可以較為準(zhǔn)確地按照既定規(guī)劃路線行進(jìn)，在已知跟蹤起始點(diǎn)狀態(tài)(X0,Y0)的前提下，在每一個采樣周期內(nèi)，結(jié)合無人智能單元在采樣周期內(nèi)的位移，將坐標(biāo)傳感器的數(shù)據(jù)轉(zhuǎn)化成為相對于跟蹤起始點(diǎn)的相對數(shù)據(jù)。即將動態(tài)觀測站轉(zhuǎn)化為定點(diǎn)觀測站的過程。轉(zhuǎn)化公式如下：

(22)

(23)

在完成定點(diǎn)觀測站的轉(zhuǎn)化后，需要對執(zhí)行跟蹤任務(wù)的無人智能單元和協(xié)同跟蹤的無人智能單元進(jìn)行狀態(tài)估計值的帶權(quán)融合，由式(21)求出的權(quán)值與式(22)、式(23)可得最優(yōu)的集群狀態(tài)估計值Xop(k)如下：

(24)

式中：Xop(k)為最優(yōu)的預(yù)測輸出，即最優(yōu)跟蹤路線。

整體算法流程如圖2所示。

圖2 無人集群目標(biāo)跟蹤系統(tǒng)流程

2 仿真結(jié)果與分析

利用坐標(biāo)轉(zhuǎn)換公式、IMM Kalman算法、集群優(yōu)化算法對目標(biāo)進(jìn)行濾波跟蹤，仿真首先在單艇的基礎(chǔ)上，分別采用了適用于非線性系統(tǒng)的EKF算法和IMM Kalman算法對目標(biāo)進(jìn)行跟蹤；然后在艇群的基礎(chǔ)上，利用基于IMM的集群優(yōu)化算法對目標(biāo)進(jìn)行跟蹤，并用蒙特卡洛方法[17]仿真30次。需要指出的是，在無人艇群場景下，由于無人艇群的任務(wù)模式是多樣的，往往包含對海域的巡視以及對可疑目標(biāo)的偵察、定位和跟蹤等。為保證艇群在任意時刻都能執(zhí)行上述任務(wù)，提出的交互式多模型跟蹤優(yōu)化算法僅限于參與跟蹤任務(wù)和協(xié)同跟蹤任務(wù)的無人艇，不是執(zhí)行跟蹤和協(xié)同跟蹤任務(wù)的其他無人艇不參與數(shù)據(jù)融合。

圖3展示了擴(kuò)展卡爾曼濾波對目標(biāo)的跟蹤軌跡，可以明顯看出，在目標(biāo)進(jìn)行慢轉(zhuǎn)彎時，EKF的跟蹤性能開始變差，并且逐漸發(fā)散，丟失跟蹤目標(biāo)，由圖4的位置估計偏差可以定量地反映出EKF在目標(biāo)進(jìn)行轉(zhuǎn)彎時對目標(biāo)跟蹤的不可靠性。這也表明單一的非線性濾波方法無法較好地適應(yīng)運(yùn)動狀態(tài)多變的目標(biāo)。

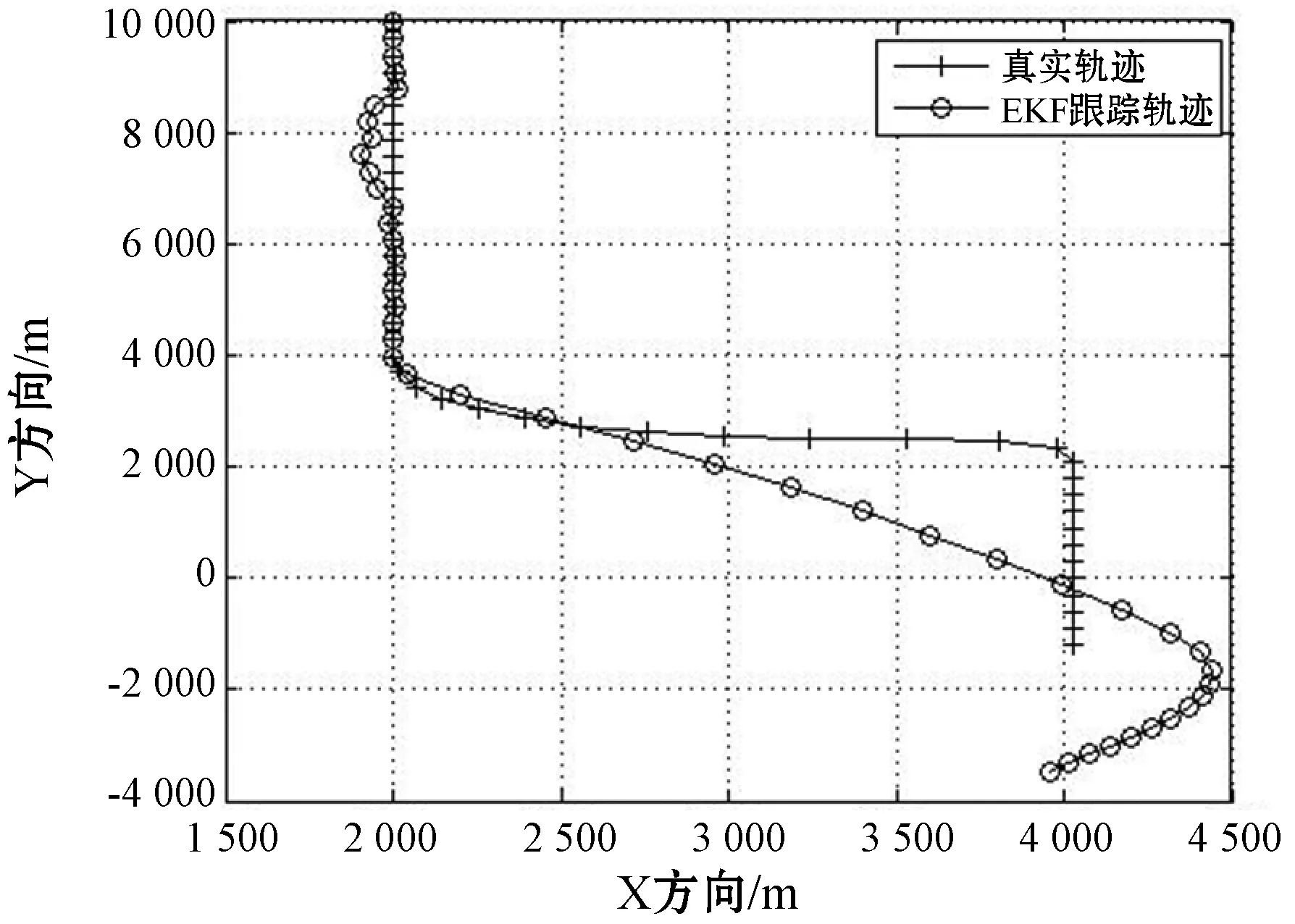
圖3 EKF跟蹤結(jié)果與真實(shí)值對比

圖4 EKF的位置誤差估計

圖5包含三條軌跡，可以看出，CIMMF算法在慢轉(zhuǎn)彎以及慢轉(zhuǎn)彎以后的勻速狀態(tài)對目標(biāo)的跟蹤路徑與目標(biāo)真實(shí)軌跡更加接近，濾去大量的噪聲，而單艇濾波算法雖大致上可以保持對目標(biāo)的跟蹤不丟失，但是兩處轉(zhuǎn)彎前后的估計值與真實(shí)值之間都有較大的偏差。即利用數(shù)據(jù)融合算法融合多無人艇的跟蹤結(jié)果與真實(shí)值更為接近。

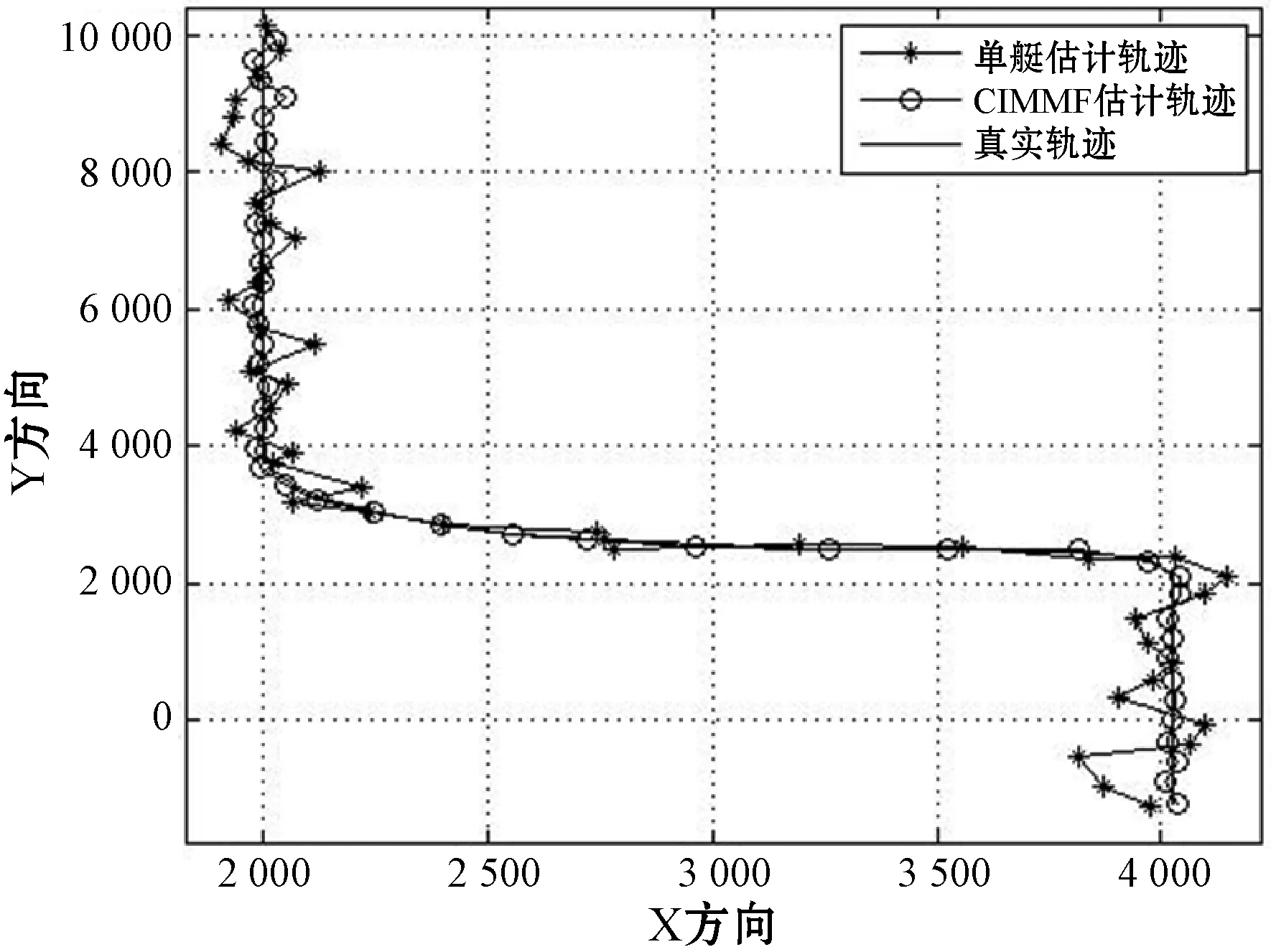
圖5 軌跡對比

由式(11)可得單艇濾波和群艇濾波分別在x方向?yàn)V波誤差均值，由式(12)可得單艇濾波和群艇濾波分別在x方向?yàn)V波誤差標(biāo)準(zhǔn)差，仿真結(jié)果如圖6、圖7所示。在x方向上，群艇濾波的輸出誤差均值比單艇誤差均值小很多，群艇濾波的輸出誤差標(biāo)準(zhǔn)差比單艇誤差標(biāo)準(zhǔn)差小很多，艇群濾波效果遠(yuǎn)遠(yuǎn)好于單艇。在t=300 s時，由于目標(biāo)在進(jìn)行急轉(zhuǎn)彎，所以單艇在此時的誤差均值最大，而群艇優(yōu)化算法大大減小了急轉(zhuǎn)彎時的誤差，對于快轉(zhuǎn)彎時的自適應(yīng)能力更強(qiáng)，艇群優(yōu)化算法使得普通IMM Kalman濾波算法在轉(zhuǎn)彎處更加穩(wěn)定，降低了目標(biāo)跟蹤丟失率。

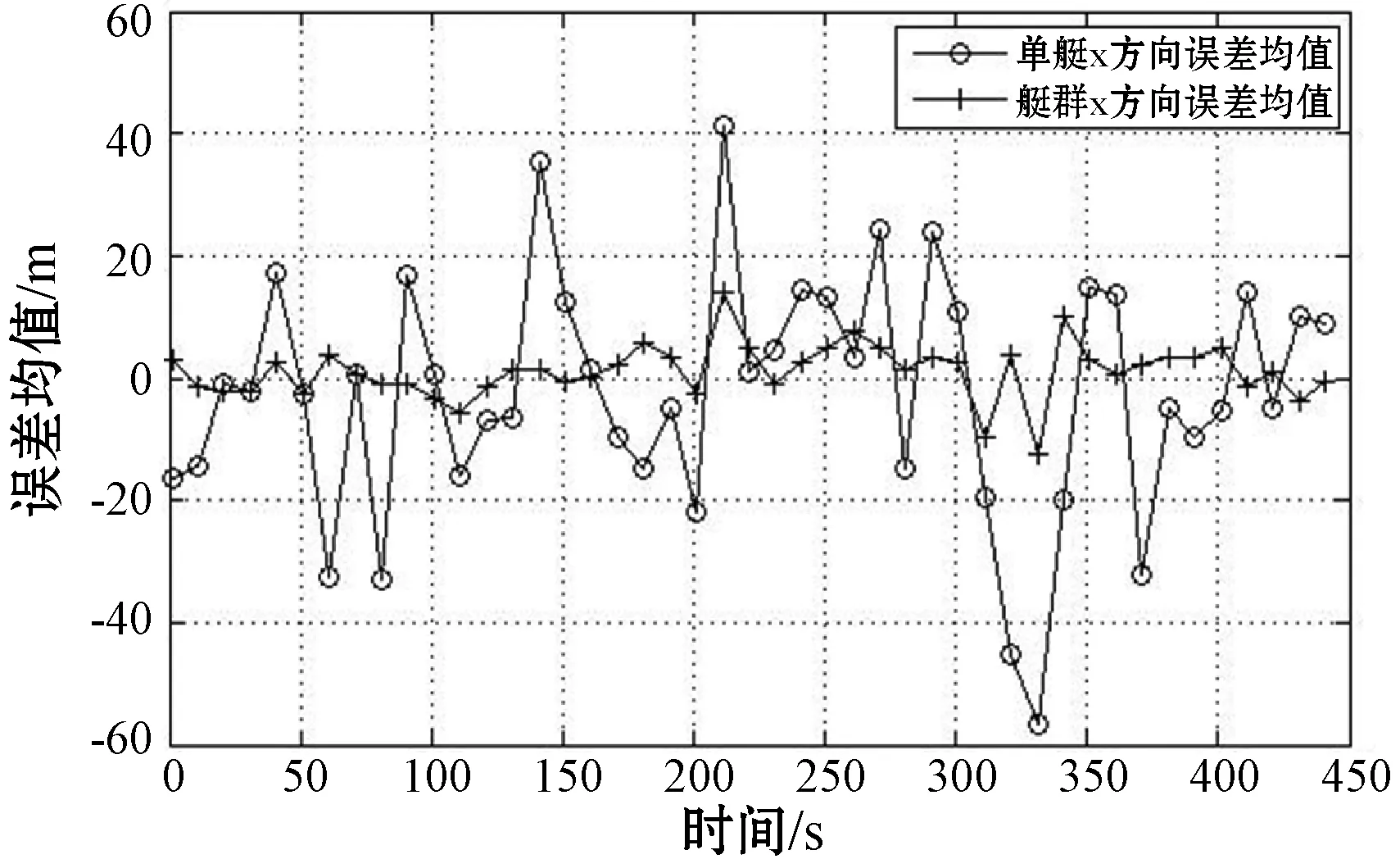
圖6 x方向誤差均值對比

圖7 x方向誤差標(biāo)準(zhǔn)差

圖8為調(diào)用不同數(shù)量的無人艇協(xié)同跟蹤目標(biāo)的誤差標(biāo)準(zhǔn)差對比，可見隨著參與協(xié)同跟蹤任務(wù)的無人艇數(shù)量的增加，IMM濾波優(yōu)化算法的狀態(tài)估計值的誤差越來越小。通過分析又可以進(jìn)一步發(fā)現(xiàn)，當(dāng)參與跟蹤和跟蹤協(xié)同任務(wù)的無人艇數(shù)量增加到3以后，優(yōu)化算法對噪聲的濾波功能顯著降低，這也表明，在實(shí)際的無人艇巡視過程中，如果出現(xiàn)可疑目標(biāo)需要派遣無人艇進(jìn)行跟蹤。為了提高艇群整體的作業(yè)效率，在可以大幅度提高對目標(biāo)的跟蹤精度和可靠性的基礎(chǔ)上，可以只派遣3艘左右的無人艇對可疑目標(biāo)進(jìn)行數(shù)據(jù)采集，其中的跟蹤無人艇對目標(biāo)進(jìn)行跟蹤。

圖8 多艇采用CIMMF誤差標(biāo)準(zhǔn)差對比

3 結(jié) 語

本文基于交互多模型卡爾曼濾波，利用極大似然估計算法和加權(quán)融合算法，既解決了無人集群在目標(biāo)跟蹤過程中，可疑目標(biāo)突然改變方向而導(dǎo)致無人單元失去跟蹤目標(biāo)的問題，又解決了無人智能單元跟蹤精度低的問題。針對集群協(xié)同跟蹤的任務(wù)模式，實(shí)現(xiàn)的是數(shù)據(jù)上的協(xié)同搜集，只有一個無人智能單元對可疑目標(biāo)進(jìn)行實(shí)際的軌跡跟蹤，這既保證了各個智能單元的任務(wù)獨(dú)立性，又體現(xiàn)了群體的協(xié)同性。搜集的數(shù)據(jù)通過極大似然估計法積分得到每個樣本值的最佳權(quán)值，經(jīng)過數(shù)據(jù)融合后的結(jié)果無論是在跟蹤可靠性還是跟蹤精度方面都有較大的優(yōu)化，更加接近目標(biāo)的真實(shí)路徑，跟蹤效果更好。本文提出的集群濾波優(yōu)化算法具有更強(qiáng)、更穩(wěn)定的自適應(yīng)能力，這種針對運(yùn)動狀態(tài)突變的算法在無人艇群、無人集群、無人駕駛等場景都有較大的應(yīng)用前景。