超越模型在比較大小問題中的應用

丁 濤

(青島市黃島區博文中學)

以函數為背景的比較大小問題,是近年高考的常考題型,多以選擇題的形式出現,且常出現在壓軸題的位置,學生因不清楚這類題目的命題原理,因此在高考有限的時間內,往往不能快速、準確地解答問題.通過深入研究,筆者發現此類問題大多以某一函數為背景,以函數的性質為切入點.因此在求解問題時只要準確構造相應的函數型,即可順利解答.筆者發現常用的函數模型有以及這兩個函數的倒數函數.下面就針對這幾個函數模型的應用進行舉例說明.

例1下列不等關系中不正確的是( ).

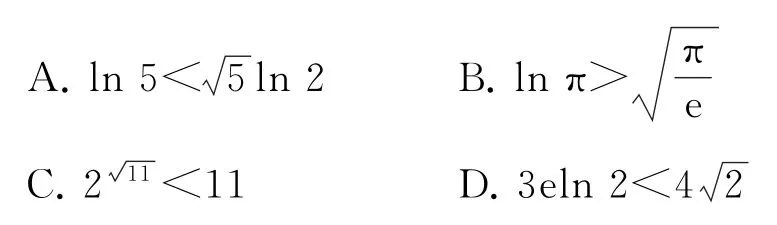
綜上,故選A.

例2已知,其中e為自然對數的底數,則a,b,c的大小關系為( ).

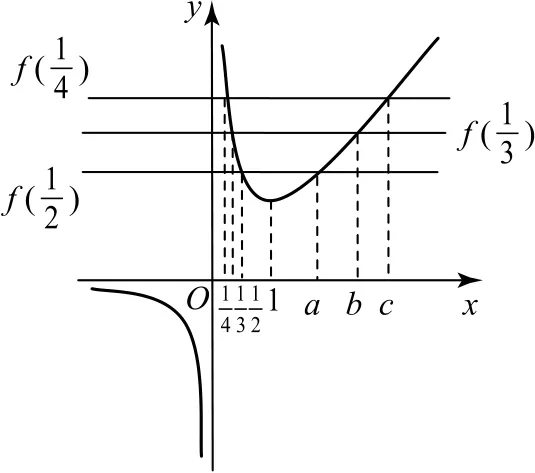
圖1

例3設,則a,b,c的大小關系為( ).

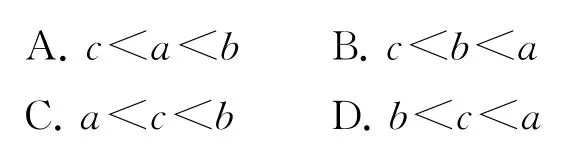
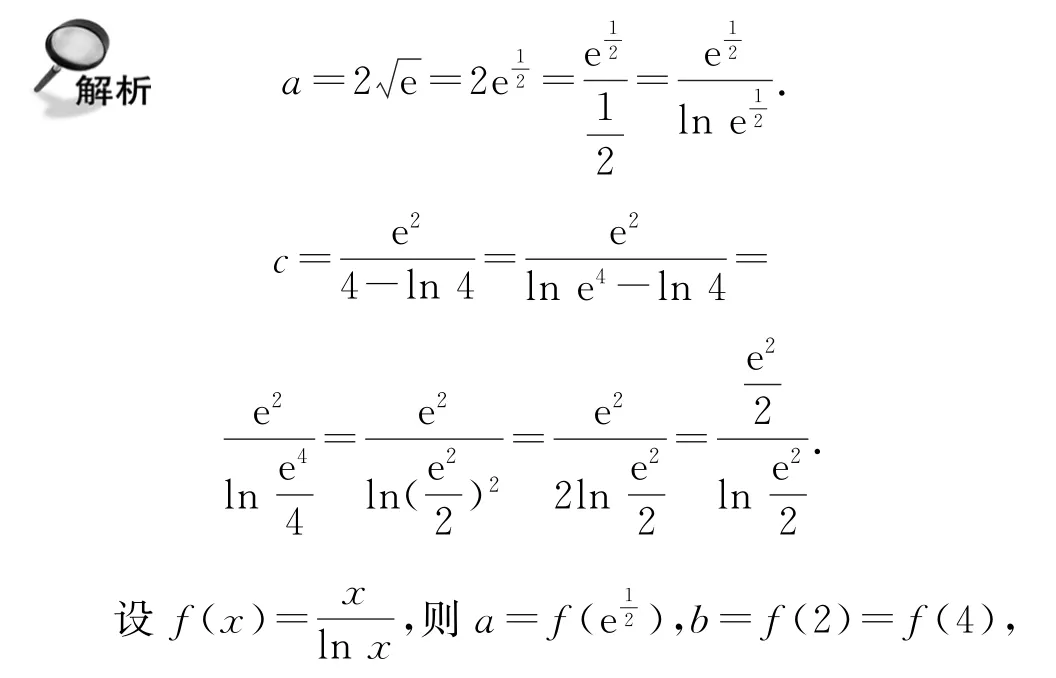
綜上,c＜b＜a,故選B.

例4已知實數a,b,c滿足b＞1,則a,b,c的大小關系為( ).

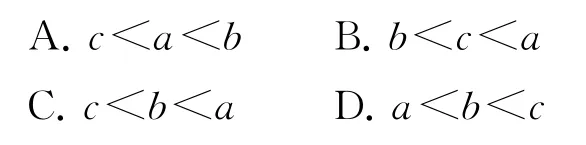
已知b＞1,即lna＞0,c＜0,所以a＞1.

設函數g(x)＝lnx－x(x＞0),求導得g′(x)＝,所以函數g(x)在區間(0,1)內單調遞增,在區間(1,＋∞)內單調遞減,gmax(x)＝g(1)＝ln1－1＝－1＜0,所以lnx＜x(x＞0),所以lna＜a,即

綜上,b＞a＞c,故選A.

處理比較大小問題,除了構造幾種超越函數模型外,還要熟悉基本指數函數、對數函數、冪函數的圖像和性質,以及不同函數之間的位置關系.

(完)