二次求導在解題中的妙用

許國慶

(黑龍江省大慶市第二十三中學)

導數及其應用是高中數學的一個重要的主干內容,也是歷年高考中的必考基本知識.利用導數及其應用解決一些相關的函數問題,當一次導函數無法直接(或很難)判斷正負取值情況時,可以通過構建新函數,利用二次導函數的正負取值情況分析與解決,這是解題常用的方法.本文結合實例加以剖析,以期指導復習備考.

1 利用二次求導判斷函數的單調性

例1已知函數,試求函數f(x)的單調區間.

分析根據題目條件,先確定函數f(x)的定義域,通過對函數f(x)求導,從導函數的分式結構出發進一步構建函數,通過二次求導來確定一次導函數的單調性與最值,從而得以確定函數f(x)的單調區間.

解由于函數f(x)的定義域為x∈(0,1)∪(1,＋∞),求導得,令函數u(x)＝,所以u(x)在(0,1)上單調遞增,在(1,＋∞)上單調遞減,故當x∈(0,1)∪(1,＋∞)時,u(x)＜u(1)＝0,即f′(x)＜0,因此函數f(x)在(0,1)和(1,＋∞)上單調遞減.

在利用導數判斷函數的單調性時,特別是導函數中的部分關系式(分式中的分子或分母中的一者易確定正負,另一者不易確定正負等情況)的符號很難直接判斷或無法確定時,可以構造新的函數,采用二次求導處理,判斷出一次導函數的符號以及最值,進而最終確定函數的單調性.

2 利用二次求導判定代數式的大小

例2若函數,0＜x1＜x2＜1,設a＝f(x1),b＝f(x2),則a,b的大小關系是( ).

分析根據題目條件,關鍵是確定函數f(x)在(0,1)上的單調性,但直接判斷單調性較困難,且求導后難以確定導函數的符號,從而考慮將一次導函數中分子所對應的關系式視為新函數,利用二次求導確定一次導函數的單調性與最值,再確定函數f(x)在(0,1)上的單調性,進而判定代數式的大小關系.

解由于函數,求導得f′(x)＝,令函數g(x)＝xcosx－sinx,x∈(0,1),求導得g′(x)＝－xsinx＜0,所以函數g(x)在(0,1)上單調遞減,則g(x)＜g(0)＝0,所以f′(x)＜0,即函數f(x)在(0,1)上單調遞減,而0＜x1＜x2＜1,則f(x1)＞f(x2),即a＞b,故選A.

利用導數判定代數式的大小,其實質就是判斷函數的單調性.對于以上問題,為得到函數f(x)在(0,1)上的單調性,需判定一次導函數f′(x)的符號,而其分母為正,那么只需判斷分子xcosxsinx在給定區間上的符號,由于很難直接判斷,故通過二次求導,判斷出一次導函數的符號,最終得以順利解決問題.

3 利用二次求導確定參數的最值(或取值范圍)

例3已知函數f(x)＝2(x－2)ex＋a(x2＋4x)＋4,其中a∈R,e為自然對數的底數.若不等式f(x)≥0在區間[0,＋∞)上恒成立,求實數a的取值范圍.

分析根據題目條件,求出函數f(x)的導數,通過對參數分a≤0與a＞0討論,當a≤0時直接確定不等式不可能恒成立;而當a＞0時,結合二次求導處理,進一步對參數分4a－2≥0與4a－2＜0討論,確定不等式是否恒成立,從而得以確定參數的取值范圍.

解對f(x)求導可得

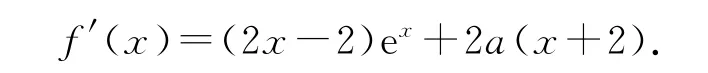
當a≤0 時,若x∈(0,1),則f′(x)＜0,所以f(x)在(0,1)上單調遞減,又f(0)＝0,所以f(x)＜0,故f(x)≥0在[0,＋∞)上不可能恒成立.

當a＞0 時,令g(x)＝f′(x)＝(2x－2)ex＋2a(x＋2)(x≥0),則g′(x)＝2xex＋2a,則g′(x)＞0,所以y＝g(x)在[0,＋∞)上單調遞增,則f′(x)≥f′(0)＝4a－2.

當4a－2≥0,即時,y＝f(x)在[0,＋∞)上單調遞增,所以fmin(x)＝f(0)＝0,故f(x)≥0在[0,＋∞)上恒成立.

當4a－2＜0,即時,f′(0)＝4a－2＜0,f′(1)＝6a＞0,故存在x0∈(0,1)使得f′(x)＝0,此時函數y＝f(x)在(0,x0)上單調遞減,又f(0)＝0,所以f(x)在(0,x0)上恒小于0,故f(x)≥0在[0,＋∞)上不可能恒成立,故不符合題意.

綜上,實數a的取值范圍

在利用導數求解參數的最值(或取值范圍)時,求解的關鍵是確定導函數的零點,如果能夠直接確定該方程的解就相對簡單一些,若求解導函數的零點有困難或無法求解時,可以考慮構建新函數,借助二次求導轉化與變形.

4 利用二次求導證明不等式

例4已知函數f(x)＝ex－x－x2,x∈(0,＋∞).求證

分析根據題目條件,通過對函數f(x)求導,此時無法確定一次導函數f′(x)的零點,進一步構建函數進行二次求導,求出二次導函數的零點并確定其符號,從而確定一次導函數的單調性,最后結合函數的極值確定一次導函數的零點,從而確定函數f(x)的單調性與最值,綜合二次函數的圖像與性質證明即可.

解對函數f(x)求導得f′(x)＝ex－2x－1,構造函數g(x)＝ex－2x－1,求導得g′(x)＝ex－2,令g′(x)＝0,解得x＝ln2.

當x∈(0,ln2)時,g′(x)＜0,當x∈(ln2,＋∞)時,g′(x)＞0,所以函數f′(x)在區間(0,ln2)上單調遞減,在區間(ln2,＋∞)上單調遞增,則

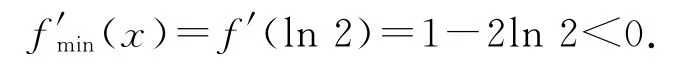
在(0,ln2)上,f′(x)＜f′(0)＝0,而在(ln2,＋∞)上,f′(1)＝e－3＜0,,所以存在)使得f′(x0)＝0,即ex0－2x0－1＝0,所以函數f(x)在(0,x0)上單調遞減,在(x0,＋∞)上單調遞增,所以

結合二次函數的圖像與性質,可知fmin(x)＞

在利用導數證明不等式時,證明的關鍵在于構造適當的函數,在一次求導后無法明確或直接求出導函數的零點時,可以通過在相應區間上用二次求導的方法判定一次導函數的符號,進而得到一次導函數的單調性,最后再利用原函數的單調性來證明相應的不等式.

在解決一些函數問題時,函數的圖像與性質雖然可以直觀地反映出兩個變量之間的變化規律,但大多數復合函數或復雜的函數作圖困難較大,這時可以借助導數及其應用,特別是進行二次求導,拓展應用函數的圖像與性質解題的空間,讓導數這個強有力的工具為函數的單調性、極值、最值等相關問題的研究提供更為簡單、程序化的方法,具有更強的可操作性、可應用性.

鏈接練習

1.(2022年全國乙卷理16)已知x＝x1和x＝x2分別是函數f(x)＝2ax－ex2(a＞0 且a≠1)的極小值點和極大值點.若x1＜x2,則a的取值范圍是________.

2.若過點P(1,λ)最多可作出n(n∈N*)條直線與函數f(x)＝(x－1)ex的圖像相切,則下列結論中錯誤的是( ).

A.λ＋n＜3

B.當n＝2時,λ的值不唯一

C.λn可能等于－4

D.當n＝1時,λ的取值范圍是

鏈接練習參考答案

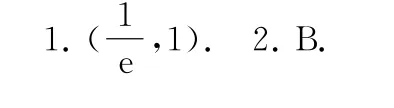
(完)