基于SSA-BP神經網絡的概率積分法預計參數求取研究

吳滿毅 徐良驥 張 坤

(1.安徽理工大學空間信息與測繪工程學院,安徽 淮南 232001;2.礦山采動災害空天地協同監測與預警安徽普通高校重點實驗室,安徽 淮南 232001;3.深部煤礦采動響應與災害防控國家重點實驗室,安徽 淮南 232001)

概率積分法預計參數與地質采礦條件密切相關,其求取精度直接影響了沉陷預計結果的精度[1-2]。近年來,不少學者采用多種方法求解概率積分法預計參數,并對算法進行了優化,取得了豐碩成果[3-6]。郭文兵等[7]采用BP神經網絡求取概率積分法預計參數,通過給定樣本建立一種網絡結構,這種結構能夠根據輸入數據盡可能準確地輸出結果,但網絡結構的不同會影響輸出結果的準確性,而網絡結構的構建依賴于各種參數變量(如隱含層個數、隱含層節點數以及訓練集和測試集的樣本大小)選取,它們都會影響最終構建的BP神經網絡,從而影響參數預計的效果。因此,需要通過科學的方法確定該類變量取值,其中比較有效的方法是優化算法。于寧鋒等[8]采用粒子群算法(Particle Swarm

Optimization,PSO)改善BP神經網絡前期的全局尋優能力,該方法能夠以較大概率保證最優解,提高概率積分法預計參數的求取精度;牛亞超等[9]采用了遺傳算法(Genetic Algorithm,GA)優化BP神經網絡,建立了GA-BP神經網絡模型求解概率積分法預計參數,該模型加快了神經網絡的收斂速度,使得概率積分法預計參數的求取精度有了進一步地提高;呂偉才等[10]采用多種族遺傳算法(Multi-Population

Genetic Algorithm,MPGA)優化BP神經網絡的權值和閾值,建立了MPGA-BP神經網絡模型,通過試驗驗證了該優化算法的有效性。上述優化算法在很大程度上克服了BP神經網絡參數選擇的困難,提高了概率積分法預計參數的求解精度,但仍然存在全局尋優能力較差且收斂速度慢等不足,降低了預計參數的求解效率。2020年,薛建凱根據麻雀覓食和反捕食行為提出了麻雀搜索算法(Sparrow Search

Algortihm,SSA),該算法尋優能力強、收斂速度快,具有較好的穩定性[11]。針對BP神經網絡求解概率積分法預計參數出現的局部最優解和收斂速度慢的問題,本研究利用麻雀搜索算法優化BP神經網絡模型結構,得到最優的權重值和偏置項,建立SSA-BP神經網絡組合預測模型,確定概率積分法預計參數。結合50組實測數據進行試驗,并將試驗結果與BP神經網絡模型相比較,驗證SSA-BP神經網絡的可靠性。

1 SSA-BP神經網絡模型構建

1.1 麻雀搜索算法

麻雀是一種小型群居性鳥類,集體覓食時會有明確的分工與合作,按照分工它們的身份可以分為發現者、加入者和偵察者[12-13]。發現者一般為整個麻雀群體尋找食物并為其提供覓食方向;加入者則是通過發現者獲取食物;偵察者則是在群體覓食時進行安全警戒,一旦有危險靠近會發出信號提醒正在覓食的麻雀,使其遠離危險。麻雀在覓食過程中會根據自己的分工和危險情況及時調整自己的位置,以適應變化[14-17]。薛建凱[11]根據麻雀群體覓食時的這些特點,提出了麻雀搜索算法,并給出了適應度求取方法。假設麻雀群有n只麻雀,每只麻雀可能出現在d維的搜索空間中,那么所有麻雀可能出現的位置就可以組成一個矩陣,即:

則n個麻雀的適應度值可以按下式求取:

式中,e為每只麻雀的適應度值,適應度值的好壞決定著麻雀種群中誰會是發現者。

發現者為了尋找食物通常比其他麻雀具有更大的搜索范圍[11],在每一次覓食過程中,發現者的位置會有如下更新:

式中,t為當前迭代次數;i表示第幾個麻雀;j為變量維數;itermax為最大的迭代次數;Yi,j表示的是第i個麻雀在第j維中的位置信息;α為隨機數,α∈(0,1];Q為隨機數,服從均值為0、方差為1的標準正態分布;L為一個1行d列的矩陣,其各元素都為1,R2為預警值,R2∈[0,1];ST為安全值,ST∈[0.5,1]。當R2＜ST時,表示麻雀覓食附近沒有威脅者,發現者可以搜索更廣泛的區域;若R2≥ST,此時偵察者發現覓食附近有威脅者,就會發出信號提醒其他麻雀,其他麻雀根據信號快速飛往安全區域。

對于加入者,在覓食過程中,它們通過監視發現者找到食物,并與發現者進行爭奪,贏了就會獲得發現者的食物;否則,繼續監視發現者。加入者的位置更新滿足如下關系:

3種類型的麻雀中,負責警戒周圍的麻雀發現危險靠近時,立刻發出信號提醒其他麻雀移動到安全區域,此時位置變化可用下式表示:

1.2 基于SSA-BP神經網絡的概率積分法預計參數求取模型

BP神經網絡是一種按誤差逆向傳播算法訓練的多層前饋網絡[8],通過獲取一定數量的樣本數據進行訓練,一直更新神經網絡的權重值和偏置項使得誤差函數沿著負梯度方向下降,直到滿足要求為止。但是其在進行非線性擬合時,容易陷入局部最優解和收斂速度慢的問題。為此,本研究利用麻雀搜索算法不斷地糾正BP神經網絡訓練時的隱含層節點數,得到最優的權重值和偏置項,以此來縮小網絡的輸出值與期望值之間的誤差,進而提高BP神經網絡的收斂速度。SSA-BP神經網絡模型流程如圖1所示。具體步驟為:①獲取實測數據,對數據進行預處理,并將數據隨機分成兩組,一組作為訓練樣本,剩下的作為測試樣本;②確定BP神經網絡的激活函數;③ 重置BP神經網絡的網絡結構參數;④ 由式(3)計算種群的適應度和最優個體;⑤ 通過覓食與反捕食行為更新個體,即由式(3)、式(4)、式(5)計算更新發現者、加入者和偵察者的位置;⑥判斷是否滿足收斂精度要求,滿足則執行下一步,否則,返回步驟(4),繼續尋找最優位置;⑦將得到的最優位置賦給BP神經網絡的權重值和偏置項,得到訓練后的模型,再輸入測試樣本進行求解和模型精度驗證。

圖1 SSA-BP神經網絡建模流程Fig.1 Flow of SSA-BP neural network modelling

2 實例測試與結果分析

2.1 模型設置與精度對比方法

2.1.1 SSA-BP神經網絡模型設置

概率積分法預計參數與地質采礦條件密切相關,本研究從文獻[1]、[7]、[9]和淮南礦區共487組采煤工作面的實測數據中均勻地選取厚松散層、中厚松散層和薄松散層共50組數據進行該模型驗證,具體數據見表1。

表1 采煤工作面實測數據Table 1 Measured data of coal mining face

續表

以H、h、M、α、N、n、f共7個地質采礦條件參數作為 SSA-BP 神經網絡的輸入值,以q、b、θ、tanβ和s/H5個概率積分法預計參數作為SSA-BP神經網絡的輸出值。將數據經過隨機函數亂序后分成兩組,一組作為訓練樣本,共有45組數據;另一組作為測試樣本,共有5組數據,用于檢驗SSA-BP神經網絡的精度。由于每個概率積分法預計參數的最優權重值和偏置項可能不同,本研究采用多輸入層單一輸出層,即7個輸入節點1個輸出節點,建立5個獨立的優化模型。經測試,確定BP神經網絡的激活函數為softlim,學習速率為0.01,發現者比例設置為0.7,剩下的為加入者,同時意識到危險的麻雀的比重設置為0.2。

2.1.2 精度對比方法

本研究通過平均絕對誤差(MAE)、均方根誤差(RMSE)和平均絕對百分比誤差(MAPE)來衡量兩個模型的求解精度[18]。平均絕對誤差用來評估求解結果和實測數據之間接近的程度,其值越小說明模型擬合效果越好;均方根誤差是指模型輸出結果和實測數據偏差的平方與測試集數量比值的平方根,其值越小說明模型精度越高;平均絕對百分比誤差是用于評價模型優劣最受歡迎的指標之一,取值范圍為[0,+∞),0表示完美模型,大于100%則表示劣質模型。具體計算公式為

式中,xi為實測值;為模型輸出結果;n為樣本數量。

2.2 結果分析

2.2.1 模型預測精度評價

BP神經網絡模型與SSA-BP神經網絡模型精度對比見表2。由表2可知:SSA-BP神經網絡模型求解的各項參數的平均絕對誤差和均方根誤差都接近0且小于1。而BP神經網絡的平均絕對誤差和均方根誤差雖然都接近0,但該模型求解的開采影響傳播角θ的平均絕對誤差和均方根誤差均大于1。由此可見,麻雀算法優化的神經網絡模型預測精度更高。從平均絕對百分比誤差上看,SSA-BP神經網絡的最大值為9.33%,比BP神經網絡的最大值小10.27%,說明SSA-BP神經網絡預計概率積分法參數精度高、模型穩定。

表2 BP神經網絡模型和SSA-BP神經網絡模型精度對比Table 2 Comparison of Accuracy between BP Neural Network Model and SSA-BP Neural Network Model

2.2.2 模型解算結果對比

經測試,得出下沉系數最佳隱含層節點數為5,水平移動系數最佳隱含層節點數為9,開采影響傳播角最佳隱含層節點數為16,主要影響角正切值的最佳隱含層節點數為20,拐點偏移距的最佳隱含層節點數為13。

模型輸出結果經整理如圖2所示。由圖2可知:SSA-BP神經網絡模型和BP神經網絡模型兩者的解算結果都能很好地接近實測數據,但SSA-BP神經網絡模型絕對誤差更小,說明其模型預測結果比BP神經網絡模型更接近實測值。

圖2 測試集輸出結果對比Fig.2 Comparison of test set output results

BP神經網絡模型與SSA-BP神經網絡模型解算結果見表3。由表3可知:SSA-BP神經網絡模型5組測試集輸出結果的最大相對誤差為21.00%,最大迭代次數為89,BP神經網絡模型輸出結果的最大相對誤差為35.00%,最大迭代次數為205,且前者相對誤差總體比后者小。說明SSA-BP神經網絡模型的輸出結果精度更高,迭代次數明顯降低。對于第49組中兩種模型求解的水平移動系數值,SSA-BP神經網絡模型求解精度不及BP神經網絡模型,這是由于每組地質采礦條件不同,其個別結果可能會出現BP神經網絡模型輸出值精度優于SSA-BP神經網絡模型輸出值的現象,但是并不影響整體的概率積分法預計參數的求取精度。

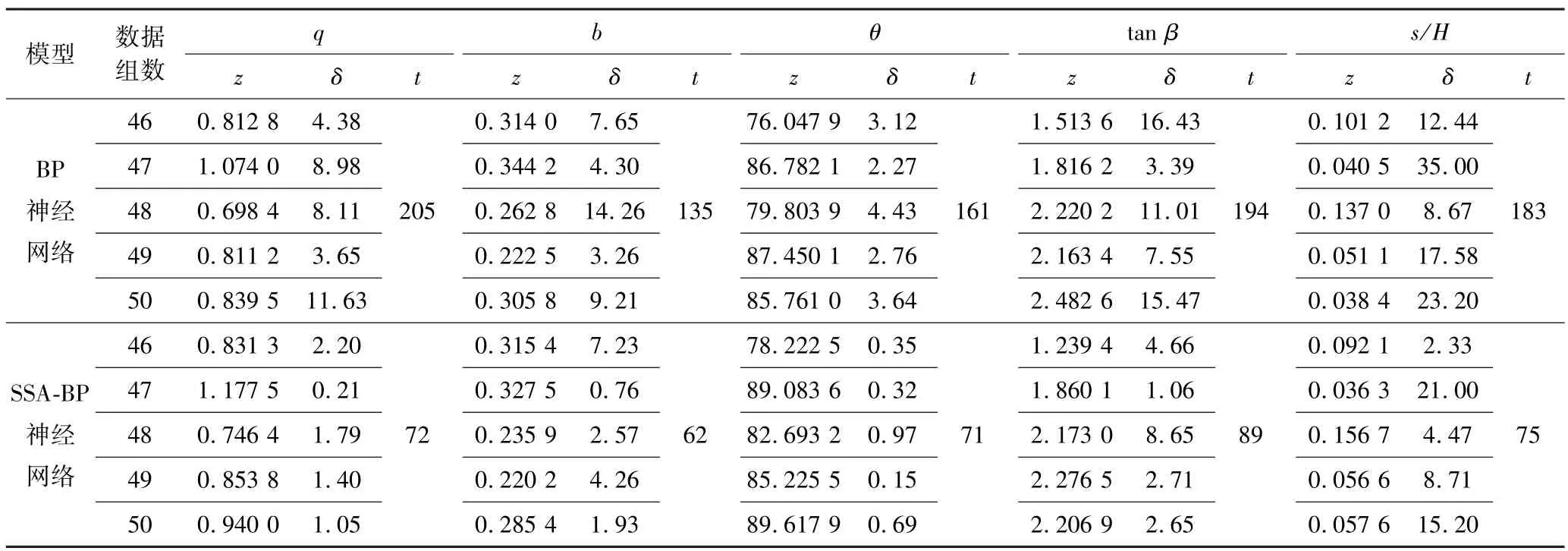
表3 BP神經網絡模型和SSA-BP神經網絡模型解算結果對比Table 3 Comparison of solution results between BP neural network model and SSA-BP neural network model

2.2.3 訓練樣本數量對模型精度的影響

為檢驗測試樣本數量對SSA-BP神經網絡模型精度的影響,利用表1實測數據,保持樣本總量不變,將測試樣本數量分別設置為3～7組,其結果如圖3所示。為方便比較,圖3中平均絕對百分比誤差換為小數形式。由圖3可知:在誤差允許范圍內,隨著測試樣本數量的增加,即訓練樣本數量隨之減少,平均絕對誤差、均方根誤差和平均絕對百分比誤差逐漸增高,這說明模型預測精度與訓練樣本數量有關,訓練樣本數量越多,神經網絡的學習效果越好,預測精度越好,反之,則越差。

圖3 測試集數量對模型精度的影響Fig.3 The influence of the number of test sets on model accuracy

3 結 論

(1)針對BP神經網絡模型求取概率積分法預計參數出現的局部最優解和收斂速度慢的問題,建立了基于SSA-BP神經網絡的概率積分法預計參數求取模型。利用SSA優化BP神經網絡模型的網絡結構,得到最優的權重值和偏置項,提高了模型收斂速度,并結合50組工作面實測數據對模型進行了驗證,同時討論了模型訓練樣本數量對模型精度的影響。

(2)經驗證,相較于BP神經網絡模型,SSA-BP神經網絡模型的MAE、RMSE和MAPE值更小,說明優化后的模型精度更高。優化后模型求解的概率積分法預計參數最大相對誤差為21%,比BP神經網絡模型的最大相對誤差小14%,且優化后的模型收斂速度更快。同時保持樣本總數不變的情況下,隨著訓練樣本數量增加,模型精度越來越高。

(3)基于SSA-BP神經網絡的概率積分法預計參數求取模型的構建,對于概率積分法預計參數精確求取有一定的參考價值,但該模型存在局部尋優能力較差的不足,后續工作中需兼顧全局尋優能力和局部尋優能力,對其進行進一步優化。