弱連接視角下的高影響力節點識別
姚月嬌 劉 向 余博文
(華中師范大學信息管理學院,湖北 武漢 430079)
面對現實生活中存在的輿論傳播[1]、疫情防控[2]、交通調度[3]等重要問題,可以將其抽象為復雜網絡進行分析,找到高影響力的因素是解決問題的關鍵環節。學者們基于不同的情境和理論提出了多種衡量節點影響力的算法,其中基于特征向量的方法同時考慮了相鄰節點的數量和質量,例如特征向量中心性算法、PageRank算法、LeaderRank算法、Hits算法等。
PageRank算法由Sergey和Lawrence提出,是目前最經典的排序算法之一。為了增強PageRank算法的適用性,姜帆[4]采用PageRank算法與引文分析方法考察了經濟管理學領域的44項國際學術獎項的中心性影響力與文獻影響力;張欣等[5]結合專利的被引次數和年齡得到了PatentRank算法;霍朝光等[6]利用PagaRank算法進行國際深度學習領域研究熱點文獻排序,強調全部關鍵詞共詞網絡的重要性;戴炳榮等[7]將公證人評價機制與PageRank算法相融合,提出跨鏈公證人機制評價模型。也有一些學者從原理層面對PageRank算法進行了改進:LeaderRank算法[8]將跳轉概率轉化為背景節點,更加靈活地解決了懸掛節點的問題;臧思思等[9]在考慮時間異質性后得到了T-PR算法并用于評價作者的學術影響力;張憲立等[10]根據反向PageRank思想和度中心性來評估節點影響力,形成啟發式算法MPRD;臧志棟等[11]融入時間異質性因子,構建了基于PageRank算法的被引時間影響因子,并以圖書情報領域的44種期刊為例進行實證研究。
盡管改進PageRank算法的研究已經不勝枚舉,但是考慮弱連接的研究不多。在度量強弱連接的研究中,Arthur A等[12]提出了IOS量表、Dibble J L等[13]提出了單維關系緊密度尺度(URCS),均通過人的主觀意識來判斷連接強度;岳增慧等[14]將節點之間的連邊權重作為連接強度,但是沒有給出區分強弱的依據;Kr?mer N C等[15]采用定性與定量相結合的方法,通過交互參數、感知到的社會支持等指標來綜合衡量連接強度,并提出連接強度應該是一個連續變量,而非二分變量。Liu Z等[16]提出,相似性是節點相互作用的依據,可以度量關系緊密程度。在此基礎上,Zhang Y等[17]利用關系強度挖掘高影響力節點,認為關系越緊密則影響力越大。但根據Mark S G提出的弱連接理論[18],不僅是聯系緊密的節點,聯系疏遠的節點也會對彼此產生一定的作用。基于此,本研究在PageRank的基礎上,根據節點相似性和弱連接理論重新構建了節點間相互影響的關系,得到了模型TransRank。通過在推特網絡、引文網絡、比特幣網絡和發明者網絡中進行SI傳染實驗,檢驗新模型的優化效果。
1 節點影響力模型
1.1 PageRank算法
PageRank算法認為萬維網中一個頁面的重要性取決于指向它的其他頁面的數量和質量,被很多高質量頁面指向的頁面也會有很高的質量。算法初始,賦予網絡中每個節點相同的PR值,并且和為1;在每次迭代時,節點需要把當前的PR值平分給指向的節點,新PR值是其收到的PR值之和;當所有節點的PR值不再變化時停止迭代。
對于網絡中出度為0的節點(稱為懸掛節點),它的PR值會隨著每次迭代不斷增長。為解決這個問題,引入一個隨機跳轉概率c,即在迭代過程中每個節點的PR值都將以(1-c)的概率均分給網絡中所有節點,以c的概率均分給它指向的節點。節點i在t時刻的PR值為:
(1)

PageRank算法中的節點會將自己的值平均分配給其指向的節點,但是不同節點對同一節點的影響力是有差異的,同一節點對不同節點的影響程度也有高低之分,所以平均分值的傳值方法不能真實反映節點之間的影響關系,由此計算出的節點PR值也不能準確表示節點在網絡中的影響力。
1.2 弱連接的影響
Hansen M T[19]將組織中密切、頻繁的直接聯系稱為強連接,疏遠、不頻繁的直接聯系稱為弱連接。1973年,Mark S G提出了弱連接理論[18],強調弱連接可以幫助人們在社會網絡中獲得重復率低、價值性高的信息,進而擴大信息交流的范圍。Abbasi A等[20]發現,弱連接可以促使節點與不同類群中的節點建立更為廣泛的關聯;牌艷欣等[21]根據引文之間的弱關系構建網絡,在此基礎上識別出的跨學科相關知識組合在指導跨學科合作上具有一定的意義。
弱連接理論可以應用到復雜網絡中計算節點之間的影響力。將兩個節點之間的聯系程度定義為連接強度,用Rij表示;將兩個節點對彼此的影響力定義為影響強度,用Eij表示。研究認為,若節點j與節點i相連,那么隨著它們的連接強度逐漸增強,雖然相互作用的頻次和強度有所提高,但它們之間的異質性會隨之降低,所以它們對彼此的影響強度會逐漸減弱;之后隨著兩個節點之間的連接強度繼續加強,相互作用的頻次和強度大幅提升,對彼此的影響強度會不斷增強。
1.3 TransRank算法
TransRank算法是本研究提出的用于衡量節點影響力的新模型,在PageRank算法的基礎上改善了傳值規則,可以抽象為網絡中各節點互相傳值的過程,于是取“傳遞”的英文“Transmit”來命名新算法。在TransRank算法初始,賦予網絡中每個節點均等的初始TR值,且和為1。然后,根據Liu Z等[16]的研究,計算每兩個節點的共同鄰居在它們所有鄰居中的比例,即節點相似性,以此判斷節點之間的關系是否緊密[22],本研究將該比例值對應為連接強度Rij,公式如下:
(2)
其中,m為節點i的鄰居數量,n為節點j的鄰居數量,k為節點i和j的共同鄰居數量。
之后,根據弱連接理論,影響強度Eij會隨著連接強度Rij變化而變化,過程類似于倒置的拋物線[23],可以用以下函數來擬合:
(3)
其中0 最后,為了防止懸掛節點不斷接收其他節點的值,每個節點以c的概率根據影響強度的比例將TR值分配給它指向的節點,以(1-c)的概率均分給網絡中所有節點。當所有節點的TR值都不再變動時迭代停止,最終節點的TR值越大,說明節點在網絡中影響力越大。節點i在t時刻的TR值為: (4) 其中,OUTj為節點j的后向節點集,INi為節點i的前向節點集。 1)設T是一個n×n的矩陣,其中: (5) 2)設R是一個包含著n個元素的向量,對應著每個節點的TR值,其中: ‖R‖=1 (6) 3)算法迭代過程如下: (7) 其中,e的長度為n、元素都是1的列向量。 4)算法迭代終止條件為: (8) 5)令: (9) 無論網絡連通性如何,T′都是一個正矩陣。根據Perron-Frobenius定理,可以得到: a.矩陣T′的最大特征值為正實數特征值λ,其絕對值是所有特征值中最大的。 b.與正實數特征值λ對應的特征向量的元素均為正。 c.矩陣T是行隨機矩陣,所以矩陣R*也是行隨機矩陣,故存在λ=1,對應的向量為e,即對于任意非零和非負的單位初始向量,都可以收斂到R*(此時R*=e)。 本研究的實驗對象是4個真實網絡數據[24]。其一,Twitter是一個在線社交平臺,用戶可以發表推文,也可以對其他用戶的推文進行評論或者轉發。本研究截取部分推特用戶之間的轉發關系,構成了推特網絡,其中推文被轉發的數量是用戶影響力的一種表現。其二,ArXiv是由康奈爾大學運營維護的一個非盈利的數據庫,學術研究人員可以將自己最新的研究成果發布到該平臺上,其中論文之間的引用可以看作是研究影響力的擴散。本研究使用1993年1月至2003年4月發表在ArXiv的有關高能物理理論的文章,并通過引用關系構建了引文網絡。其三,Bitcoin-OTC是人們進行比特幣場外交易的線上市場,其中的用戶都是匿名的,為了維護交易秩序,用戶需要在每次交易完成后為彼此評分,被多次評分的用戶活動廣泛,會在市場中產生一定程度的影響。本研究選擇了一些匿名用戶及其評論關系,構成了比特幣網絡。其四,美國專利數據庫收錄了1790年至今的美國專利全文,本研究提取了化學領域1978—2002年的專利數據,根據專利發明者之間的引用關系構建了發明者網絡。 各個網絡的特征如表1所示,它們的數據規模和平均度、最大度和平均聚類系數等網絡特征均有較大的差異,具有一定的代表性。 表1 實驗網絡數據特征 本研究根據式(4)與(1)計算出了每個實驗網絡中各節點的TR值和PR值,值越大表明節點的影響力越大。在每個實驗網絡中,分別按照TR值和PR值由大到小排列所有節點,排名較前的節點被視為對應算法識別出的高影響力節點。 為了檢驗TransRank算法識別出的高影響力節點是否具有更高的影響水平,本研究選擇SI模型,每個節點只會保持易染態或者從易染態轉變為感染態。將識別出的高影響力節點作為初始感染節點,根據一定的感染率開始傳染進程,感染節點會逐漸增多并達到穩定,感染的速度和范圍可以體現出算法的優劣。具體實驗過程如下: 實驗初始,設定SI的模型兩個參數,感染率p和初始感染范圍α。感染率p可以代表不同的影響情境,比如不同的疾病傳染力大小;初始感染范圍α可以表示影響力的不同等級,α的值越小,說明節點的排名越靠前,在網絡中的影響力就越大。 其次,確定初始感染節點集。先提取出兩種算法排序結果中前α的節點集P和T,再剔除重復節點,得到初始感染節點集P′和T′。 再次,比較傳染進程。設定兩個算法的跳轉概率c為0.85,SI模型的感染率p=0.2、初始感染范圍α=2%,結果如圖1所示。 最后,觀察SI模型參數變化對算法優化效果的影響。定義優化值β來更加直觀地反映兩個算法感染效果的差距,計算公式如下: (10) 其中,TI(k)和PI(k)分別表示由初始感染節點集T′和P′在傳染到第k代時的感染比例。 檢驗TransRank算法在不同影響情境中的優化效果時,初始感染范圍α控制為2%(比特幣網絡中控制為3.5%),感染率p分別取0.1、0.2、0.3、0.4,結果如圖2所示;檢驗TransRank算法在挖掘各級影響力節點的優化效果時,感染率p控制為0.2,初始感染范圍α以0.5%為單位從0.5%遞增到6%,結果如圖3所示。圖2、圖3中的橫坐標為傳染代數(iters),縱坐標為優化值β,不同顏色的線條表示不同的參數取值。 在圖1中,TransRank算法對應的曲線始終高于PageRank算法對應的曲線,但在子圖B、C、D中,兩個算法對應的曲線會達到相同的穩定值。以上說明,TransRank算法在3個真實網絡中對應的傳染進程均明顯快于PageRank算法,在推特網絡中的感染范圍也大于PageRank算法。 圖1 兩種算法的傳播效果 在圖2中,前3個子圖里曲線的形態均為先升高再降低最后保持平穩,最后1個子圖中的曲線一直升高最后保持平穩,取值均不小于0。這說明在不同的網絡中,基于不同的感染率,TransRank算法的傳染速度都優于PageRank算法,最終感染范圍也不會劣于PageRank算法。 圖2 不同感染率下兩種算法的傳播效果 在圖3中,每一列圖像代表1個網絡的全部實驗數據,其中絕大多數的曲線分布在0值以上。說明在不同的網絡中,基于不同的初始感染比例,TransRank算法的傳染速度很大概率優于PageRank算法,最終感染范圍很少會劣于PageRank算法。 綜上所述,TransRank算法具有明顯的優化效果,但是會受到SI模型參數變化的影響。 根據TransRank算法和PageRank算法計算出實驗網絡中每個節點的TR值和PR值后,按照大小順序進行排列。由于網絡中節點數量巨大,為便于比較,不妨選擇排名前2%的節點作為高影響力節點。推特網絡中,共有467個高影響力節點,剔除相同節點后,兩種算法各剩余31個節點,如表2所示;引文網絡中,共有555個高影響力節點,剔除相同節點后,兩種算法各剩余9個節點,如表3所示;比特幣網絡中,共有117個高影響力節點,剔除相同節點后,兩種算法各剩余1個節點,如表4所示;發明者網絡中,共有162個高影響力節點,剔除相同節點后,兩種算法各剩余1個節點,如表5所示。 表2 推特網絡中的高影響力節點 表3 TransRank算法在引文網絡中識別的高影響力節點 表3(續) 表4 TransRank算法在比特幣網絡中識別的高影響力節點 表5 TransRank算法在發明者網絡中識別的高影響力節點 在推特網絡和發明者網絡中,TransRank算法識別的高影響力節點集在入度和聚類系數方面平均值較低,在出度方面平均值較高,說明這些節點更擅長面向多類節點傳播自身影響力。TransRank算法在引文網絡中識別的高影響力節點集有更高的入度平均值和出度平均值,其聚類系數平均值略低于PageRank算法識別的高影響力節點集,表明這些節點不僅會受很多節點影響,還會將自身影響輻射到周圍許多節點。在比特幣網絡中,TransRank算法識別的高影響力節點在聚類系數、入度和出度方面均有更高取值,從而有更多樣的影響對象。綜上,TransRank算法識別的高影響力節點有更為廣泛的影響覆蓋面。研究還選擇了5%和10%的比例進行分析,結果和結論沒有改變。 具體來看,以發明者網絡為例,TransRank算法識別的高影響力節點為發明者、澳大利亞科學家巴里·馬歇爾,與羅賓·沃倫一同發現了幽門螺桿菌以及這種細菌在胃炎和胃潰瘍等疾病中的作用,被授予2005年諾貝爾生理學或醫學獎。1978—2002年,巴里·馬歇爾在化學領域共申請成功了7項專利,均有關于腸胃內的微生物和分泌物。由于他沒有較高的被引量和施引量,所以被PageRank算法識別為邊緣節點。但是根據TransRank算法,巴里·馬歇爾被標記為高影響力節點,體現出了他在該領域的重要地位。 圖2代表著在4個網絡中不同感染率下TransRank算法的優化效果,每個圖像中的4個曲線表示不同的感染率,取值越大則表示TransRank算法越有利于影響力傳播。圖2A和2D中曲線的取值始終大于0,說明對于不同的影響情境,TransRank算法在推特網絡中識別出的高影響力節點既有較快的影響速度,又有較大的影響范圍。在圖2B和2C中,曲線在前期均高于0,在后期平穩時取值為0,說明在引文網絡和比特幣網絡中,TransRank算法識別出的高影響力節點擁有更快的影響速度。 在所有實驗網絡中,TransRank算法識別的高影響力節點均有更快的影響速度,可以迅速發揮自身影響力;同時,這些節點的影響范圍不會低于PageRank算法識別出的節點,可以將影響力擴散到與PageRank算法相同甚至更廣泛的區域。綜上,不論環境是否有利于影響力傳播,TransRank算法的優化效果都很明顯。 圖3比較了TransRank算法在4個網絡中不同初始感染比例下的優化效果,每個網絡都包含12條曲線,每條曲線對應一個初始感染比例α,比例越小則選出的節點影響力越大。 在推特網絡中,當α等于0.5%和2.5%時,曲線會上升并在最高點保持平穩;當α等于1%、2%、3.5%和6%時,曲線會有少許的上下波動,以上6種初始感染比例對應的優化值都始終大于0,說明TransRank算法在速度和范圍上均優于PageRank算法。當α等于3%時,曲線先上升后下降,最后在0值保持平穩,說明兩算法的最終感染范圍相同但TransRank算法的感染進程更快;當α取其他值時,曲線會下降并在最低點保持平穩,并且大部分處于0值以下,說明TransRank算法在速度和范圍上均比PageRank算法差。由上可知,在多數初始感染比例下,TransRank算法在推特網絡中識別的節點會有更好的影響效果。 在引文網絡中,當α等于1.5%、2%、2.5%、4.5%和5.5%時,曲線會先上升后下降,最后在0值處保持平穩,說明TransRank算法的傳染速度更快,但兩種算法的感染范圍一致;α等于3%、3.5%、4%、5%和6%時,曲線大致是先下降后上升最后在0值處保持平穩,說明PageRank算法的傳染速度更快,而兩種算法的感染范圍相同;當α取其他值時,曲線會下降并在最低點保持平穩,說明TransRank算法在速度和范圍上都較差。對于大多數的初始感染比例,兩個算法在引文網絡識別的節點的影響范圍一致,其中半數情況下TransRank算法識別的節點有更快的影響速度。 在比特幣網絡中,當α為0.5%、1%、2%、2.5%、3%和4.5%時,兩個算法識別出的節點完全一致,所以沒有對應的曲線;當α為1.5%、3.5%、4%、5%和6%時,曲線會先上升后下降,最后在0值處保持平穩,說明TransRank算法的傳染速度更快,兩種算法的感染范圍相同;當α為5.5%時,曲線先下降后上升,最后在0值處保持平穩,說明PageRank算法的傳染速度更快,兩種算法的感染范圍相同。由此可知,在比特幣網絡中,在半數情況下,兩個算法識別節點的影響效果一致;在部分情況下,TransRank算法識別的節點會在影響速度上表現更好。 在發明者網絡中,當α為0.5%、2%、2.5%、3%、4%和5.5%時,兩個算法識別出的節點完全一致,所以沒有對應的曲線;當α為1%時,曲線先上升,然后在最高點保持平穩,說明TransRank算法的傳染速度更快、感染范圍更廣;當α為1.5%、3.5%時,曲線一直貼合于0值,說明兩個算法效果相當;當α為5%時,曲線先下降后,稍微回升,最后在0值處保持平穩,說明TransRank算法的傳染速度更快,兩種算法的感染范圍相同;當α為4.5%和6%時,曲線會先在0值下起伏,最后在0值處保持平穩,說明PageRank算法的傳染速度更快,兩種算法的感染范圍相同。由此可知,在發明者網絡中,在多數情況下,兩個算法識別節點的影響效果一致;在部分情況下,TransRank算法識別的節點會在影響速度上表現更好。 表6匯總了在4個網絡中不同初始感染比例下TransRank算法的優化效果,從中可以清晰看到,當選擇排名前2%或者2.5%的節點時,TransRank算法的優勢會穩定地體現出來;在選擇其他α值時,TransRank算法也只會在部分實驗網絡中表現較差,大多數情況下都會在影響速度上優于PageRank算法。 表6 不同網絡中在不同初始感染比例下的優化效果 相對于其他網絡,引文網絡的優化效果較差,可能是因為引文網絡的平均度更大,節點之間的聯系更加密集和頻繁,弱連接的比例較低。推特網絡的優化效果最好,原因可能是該網絡聚類系數較低,節點較為分散,主要是通過弱連接進行聯系。 實驗顯示TransRank算法的影響效果普遍較好,那么這是不是弱連接發揮的作用呢?為驗證此想法,將節點集T′和指向它的節點集toT′都提取出來,計算弱連接連邊對識別重要節點的貢獻率γ(連接強度為0的連邊集傳給節點i的值占節點i接收總值的比例),結果如表7所示。 表7 不同網絡中弱連接對兩種算法貢獻率的比較 在4個實驗網絡中,節點集T'和toT′之間的弱連接均占有很高的比例,是節點接收值的主要途徑。同時,相較于PageRank算法,TransRank算法會賦予節點集中絕大部分節點更大的值,并且經由弱連接接收到的值更大、貢獻率更高。以上說明,弱連接確實在識別重要節點時發揮了很大的作用,幫助改善了算法的準確性和有效性。 本研究根據弱連接理論提出了新的節點影響力模型TransRank算法。新算法識別出的高影響力節點會將影響力擴展到更廣的范圍中,通過在推特網絡、引文網絡、比特幣網絡、發明者網絡4個真實網絡中進行SI傳播實驗,發現新算法可以有效地改善影響速度,即在同樣的時間里基于相同影響力的節點群開展感染進程,TransRank算法影響到的節點數量更多。同時,新算法也有可能擴大影響范圍,即從相同影響力的節點群開展感染進程,TransRank算法影響到的節點數量更多。在此基礎上,不論所處的情境是否有利于影響力的傳播,TransRank算法的優化效果都不會改變;對于不同影響等級的節點集,TransRank算法大概率會優于PageRank算法,其中當初始感染比例為2%和2.5%時,優化效果會更加明顯和穩定。 目前,本研究還存在以下不足:首先,只是在無權有向網絡中進行了算法檢驗并得到了較好的結果,還需要在加權網絡和無向網絡中開展實驗,驗證TransRank算法的普適性;其次,只考慮了在靜態網絡中挖掘高影響力節點,忽視了節點影響力的動態變化。在未來的工作中,將繼續考察TransRank算法在不同類型網絡中的表現,并探索節點影響力的演化軌跡,繼續完善模型以識別出動態更新的高影響力節點集。1.4 TransRank算法收斂性
2 實 驗
2.1 數 據

2.2 實驗過程
2.3 實驗結果
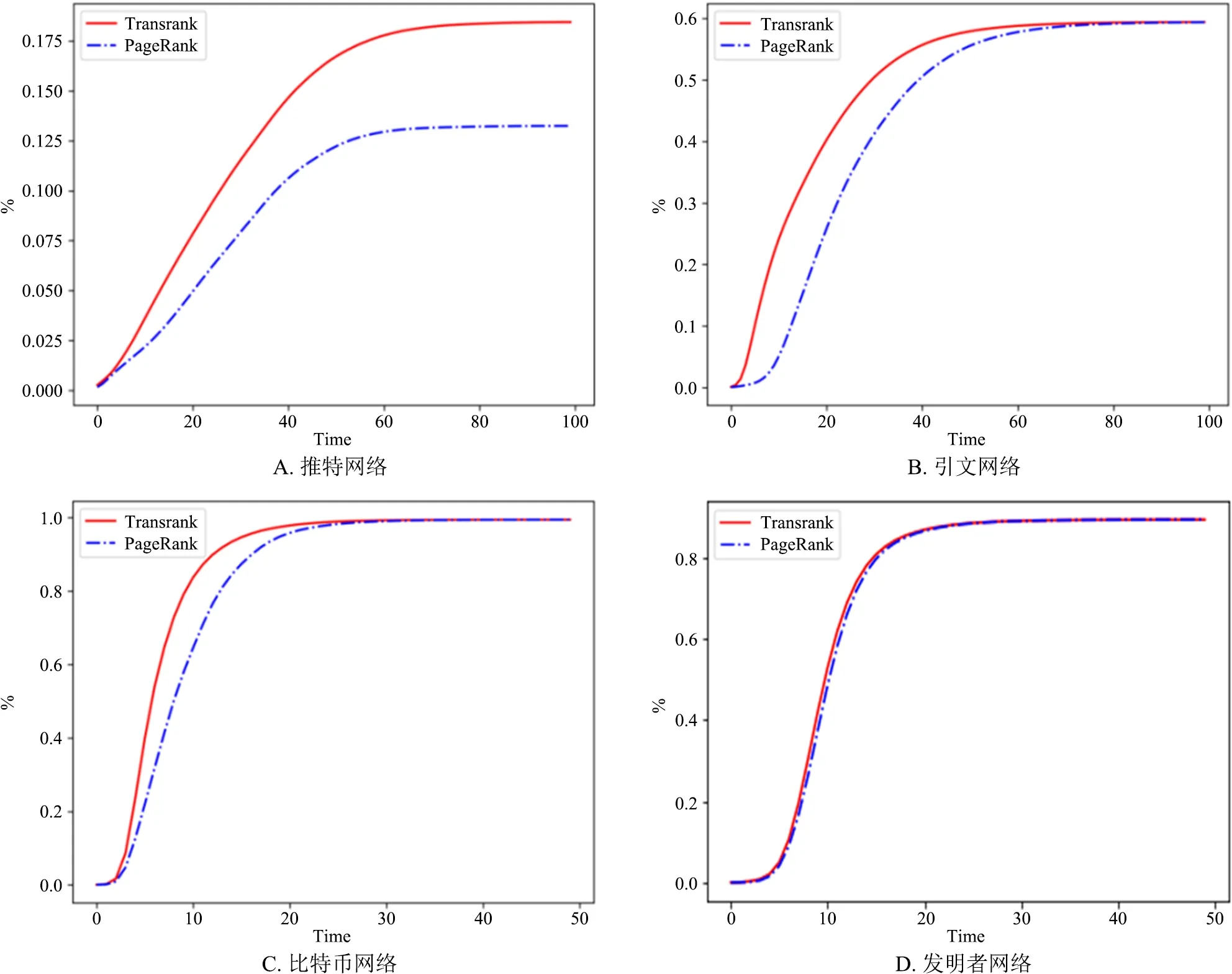

3 討 論
3.1 高影響力節點
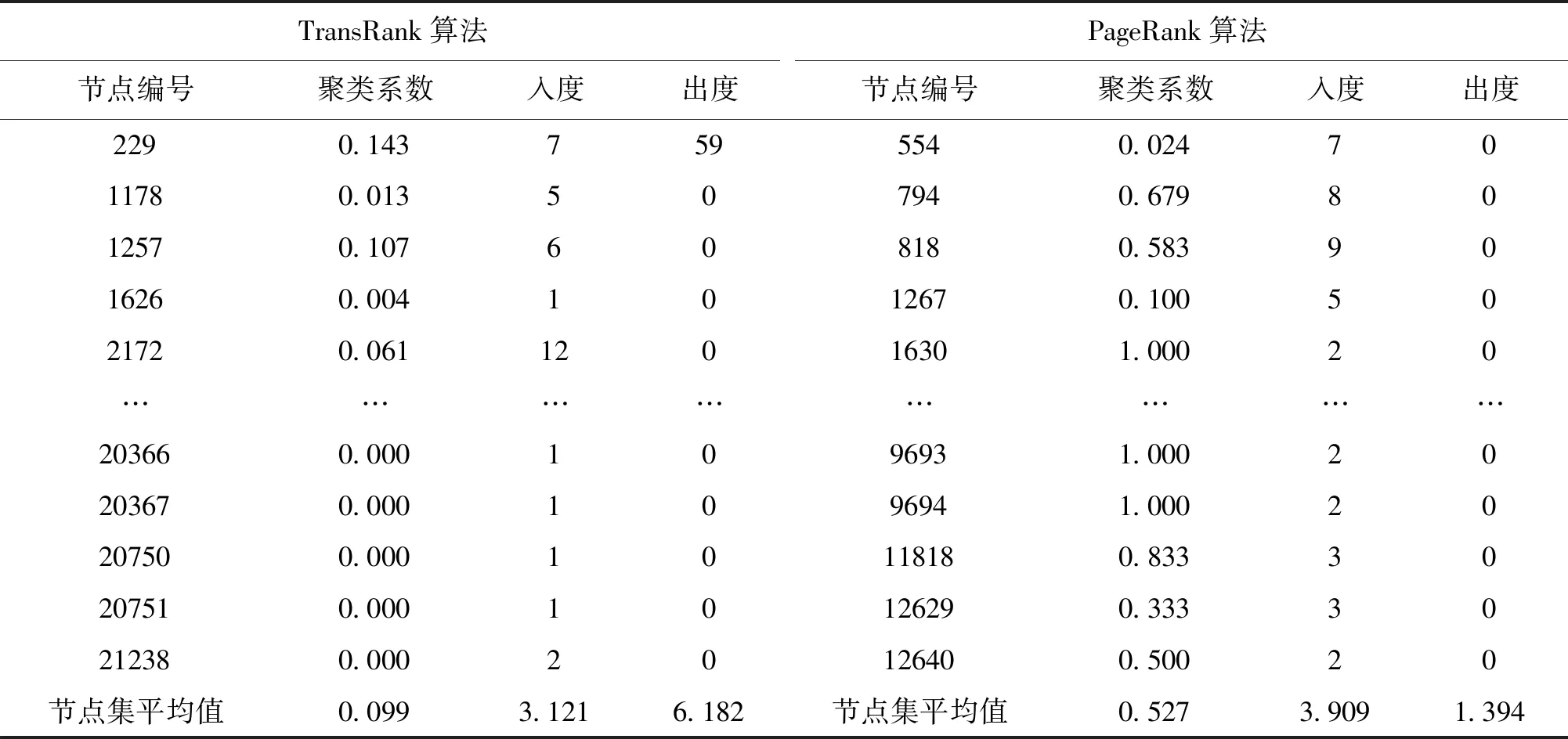




3.2 不同影響情境
3.3 不同影響等級

3.4 弱連接的作用

4 結 語

