一種無刷雙饋電機匝數配合的半解析優化方法*

李雨莎， 王淑紅， 白崟儒

(太原理工大學 電氣與動力工程學院， 山西 太原 030024)

0 引 言

目前風電領域的主流機型為永磁同步電機(PMSM)和雙饋感應電機(DFIG)。與之相比，無刷雙饋電機(BDFM)由于其擁有變頻器容量小，沒有電刷和滑環，系統運行的成本低，可靠性高，并有多種運行狀態的特點，因此在變速恒頻發電以及變頻調速領域均擁有廣闊的應用前景[1-2]。

BDFM與常規交流電機的不同之處在于其定子上有兩套繞組，功率繞組(PW)直接與電網相連，控制繞組(CW)經變頻器與電網相連，兩套繞組極對數不同，之間沒有直接的電磁耦合聯系，通過轉子進行能量轉換。兩套繞組匝數的合理配合有利于提高電機各項性能。為了提升電機運行性能，Xiong等[3]根據齒諧波和正弦繞組的原理，提出了一種不等匝雙層線圈的設計方法，并通過仿真和試驗驗證了所提出的轉子結構設計方法的有效性。任泰安等[4]基于齒諧波原理提出了一種采用不等匝數同心式轉子繞組的BDFM，推導出了適用于各種繞組分布系數的計算方法,并制造了一臺新型不等匝數同心式轉子繞組的BDFM試驗樣機。戈寶軍等[5]基于齒諧波原理和不等匝繞組理論,提出一種基于混合式轉子結構的多跨距復合式的無刷雙饋發電機轉子設計方案，有效地提高轉子導體利用率以及功率繞組的輸出功率，并以一臺450 kW電機為例具體分析。文獻[6]通過改變轉子繞組每相有效匝數來改變轉子電阻折算值的大小，從而實現與串電阻起動類似的起動過程和效果。文獻[7]推導出軟起動型繞線式BDFM較為通用的極槽配合選擇原則，設計了3種不同結構的功率繞組，通過MATLAB軟件對比分析3種不同結構繞組應用于電機軟起動時的起動特性并制作樣機進行試驗驗證。綜上所述，現有文獻大多針對BDFM的轉子繞組結構及匝數進行優化設計，而對定子兩套繞組匝數配合的研究較少。

目前無刷雙饋電機定子兩套繞組的匝數選取沒有明確的方法，主要依靠大量的有限元仿真或借鑒異步電機的經驗，計算工作量大，耗時很長。同時，由于BDFM含有定子兩套繞組及轉子繞組共三套繞組，與其他類型電機相比，其發熱問題更為突出。因此，本文提出了一種以熱負荷為優化目標的BDFM定子繞組匝數配合的半解析優化方法：通過公式解析獲得滿足同一最大功率的所有匝數配合，經解析篩選及有限元仿真的細化篩選分析，最終得到一組最佳的匝數配合。與完全依靠有限元仿真的匝數優化方法相比，該半解析優化方法減少了工作量，節約了優化設計時間與計算資源。

1 定子繞組匝數配合優化

1.1 約束條件及優化目標的解析推導

設BDFM在穩態狀態下功率繞組電流為

(1)

控制繞組電流為

(2)

式中:Isp、Isc分別為兩繞組產生電流的有效值；ωp、ωc分別為兩繞組旋轉磁場電角速度；γ、β分別為兩繞組電流初相角，超同步運行時取“+”，亞同步運行時取“-”。

以超同步運行狀態為例，兩套繞組建立的氣隙磁場轉換到轉子坐標系下為

(3)

式中:Bspm、Bscm分別為兩繞組產生的氣隙磁密幅值；ω為轉子電角速度；pp、pc分別為兩繞組極對數；α為功率繞組A相與控制繞組U相的夾角;θ為轉子坐標系下位置；ε為功率繞組A相與轉子一號嵌套單元軸線的夾角。

定轉子角度關系如圖1所示。

圖1 定轉子參考系位置關系

在忽略轉子短路環電阻的情況下，由磁通連續性定理可知，每個短路環匝鏈的定轉子磁通大小相等方向相反，對轉子坐標系下轉子電流產生的磁場進行傅里葉分解，得到其pp次磁密分量為[8]

(4)

pc次磁密分量為

(5)

轉子導條可以看作等效繞組，轉子磁場即為等效繞組中流過電流所產生的磁場，分析其中一相，則轉子產生的A相pp次磁場的等效電流可以表示為

(6)

pc次磁場的等效電流可以表示為

(7)

式中：Np、Nc分別為兩繞組每相串聯匝數；kwp、kwc分別為兩繞組的繞組系數；Ispm、Iscm分別為兩繞組電流幅值。

(8)

(9)

忽略定子繞組電阻及漏感，令端電壓等于感應電動勢：

(10)

(11)

則式(10)可以進一步化簡為

(12)

對式(12)解方程組，可得：

(13)

超同步運行時，定子功率繞組坐標系下電壓與轉子坐標系下等效電壓可以表示為

(14)

將式(14)代入式(13)，Uar=Ua，Uur=Uu，可得定子繞組電流與電壓的關系式：

(16)

(17)

由式(16)和式(17)，可以進一步推導得到超同步運行時BDFM的總電磁功率為[9]

sin(φa+φu+ppε+pcε-pcα)

(18)

電機各角度關系代入后，令φa=0°，則當φu=340°時，BDFM的電磁功率達到最大值，后續理論分析及仿真均在此角度下進行。

熱負荷的大小直接影響到電機的發熱和溫升，熱負荷值越大，電機的發熱和溫升就越高。因此，在電機實際性能優化過程中，希望能在保證輸出同樣電磁功率的情況下，電機具有盡可能小的熱負荷，從而獲得盡可能低的溫升。

根據熱負荷公式，忽略其他諧波磁場，根據式(16)和式(17)，BDFM的熱負荷可以表示為

(19)

式中：ρ為導體材料電阻率；D為定子內徑；S為定子繞組每槽面積；Z1為定子槽數；Isp、Isc為定子兩繞組電流有效值。

對于式(18)與式(19)，電磁功率Pe與熱負荷Q均是關于Np、Nc的表達式，在匝數優化過程中，保持BDFM的結構尺寸、繞組型式、各角度關系、定子繞組槽滿率和電壓規格等各項參數均不變，則最大電磁功率是僅關于定子繞組匝數Np、Nc的二元函數，即優化設計變量僅為Np、Nc。同樣后續進行有限元仿真時，電機結構尺寸等各項參數均不變，僅每相串聯匝數改變，從而保證了匝數優化前后的可對比性。

優化過程中，以最大電磁功率一定為約束條件，以Np、Nc為優化設計變量，可以得到滿足同一最大功率的所有匝數配合，以熱負荷最小為優化目標，通過理論與仿真的多次篩選與分析，最終在大量滿足約束條件的匝數配合中選出一組熱負荷最小的匝數。

1.2 求解滿足約束條件的匝數配合

以未經過匝數優化的Y280 BDFM為例進行分析，模型基本參數如表1所示，有限元模型如圖2所示。

表1 Y280 BDFM模型基本參數

圖2 Y280 BDFM有限元模型

式(18)可以簡單表示為Pemax=f(Np,Nc)，做出最大功率與Np、Nc的函數圖如圖3中的黑色曲面所示，將電機的功率約束值也畫在同一函數圖中，即圖3中的功率給定值。兩曲面的交線即為滿足該最大功率約束條件下的所有匝數配合，即交線上的每一組匝數配合均可以保證電機具有理論上相同的最大電磁功率。由于滿足約束條件的匝數配合眾多，此處不便一一列出。

1.3 排除不合實際的匝數配合

首先，為保證優化前后的可對比性，以及滿足電機的實際運行要求，合理匝數配合應滿足以下條件：

圖3 兩套繞組匝數變化時的電磁功率

(1) 不改動電機外形尺寸的情況下，繞組匝數可以放入原電機模型，保證繞組型式、節距等與原來一致，不會出現分數槽等問題。

(2) 若存在多條并聯支路時，基波旋轉磁場在各條支路中產生的感應電動勢應保持大小及相位相同，避免各支路間環流問題[10]。

排除不滿足上述兩個條件的匝數配合之后，剩余匝數配合結果如表2所示。

表2 Y280 BDFM匝數解析結果對比

其次，排除不能使電機正常運行于雙饋同步狀態的匝數配合。

由表2可見，某些匝數配合下誤差很小，某些匝數配合下誤差很大，并隨著兩套繞組匝數差距的增加而偏差增大。以下分析其原因，電機端電壓與匝數、頻率、磁通之間的關系如下：

U≈E=4.44fNΦ

(20)

將磁通Φ展開，式(20)可以表示為

(21)

式中:B為磁密；l為軸向長度。

當端電壓給定時，電機外形尺寸固定，由式(21)可以得到磁密與極對數、頻率和匝數的關系式：

(22)

根據BDFM的基本原理可知，其氣隙中包含兩種極對數的磁場(pp對極和pc對極)，而異步電機氣隙中只存在一種極對數磁場。若氣隙中兩種磁場大小懸殊，則磁場過大的這一極對數磁場將起主要作用，而另一極對數磁場作用微弱，使BDFM運行狀態接近異步運行狀態，與式(18)、式(19)所推導的雙饋同步狀態不符，則該組匝數不應選擇。

經研究表明，雙饋運行時經轉子調制后氣隙磁場中兩種基波磁場比值在0.2～5之間為宜[9]。按照該磁場比值關系進行排除，可以發現，選擇范圍內的各組匝數配合的解析值與仿真值誤差較小，說明該方法在雙饋同步狀態下可以有效指導匝數優化。

排除不滿足上述兩個條件的匝數配合，并排除近似異步狀態的匝數配合之后，剩余匝數配合結果如表3所示。

表3 Y280 BDFM滿足約束條件且符合實際的匝數配合

1.4 通過優化目標篩選

將各組滿足約束條件并符合實際的匝數配合(表3中的配合)代入優化目標式(19)，可計算得到分別采用這些匝數配合時電機的熱負荷值。由于解析過程無法考慮到電機鐵心飽和、定轉子開槽、集膚效應等各種非線性問題，解析計算結果不可避免會存在一定的誤差，因此篩選出優化目標值(即熱負荷值)前3組或前5組較小的匝數配合，然后進入有限元仿真的進一步細化篩選，以求避免漏失最優匝數配合結果。

對于Y280 BDFM，經解析方法篩選出熱負荷前三小的匝數配合為96/540、108/480和120/432。

1.5 仿真細化篩選

運用有限元仿真軟件，對上述篩選出的三組匝數配合進一步細化篩選，選出其中仿真熱負荷最小的一組匝數。圖4為解析篩選得到的三組匝數，經有限元仿真得到的定子繞組感應電動勢與電流波形。表4為根據電流及感應電動勢進一步計算得到的電磁功率、熱負荷、效率等數據，以及定轉子上的各項損耗平均值。由圖4和表4可知，匝數配合Np/Nc=108/480是這三組匝數配合中熱負荷仿真值最小的，與表3解析結果一致。

圖4 匝數配合細化篩選仿真結果

表4 Y280 BDFM匝數篩選細化仿真結果

因此，對于Y280 BDFM，利用本文的匝數配合優化方法，以最大電磁功率一定為約束條件，以熱負荷最小為優化目標，最終選取的匝數配合為108/480，該組匝數是滿足給定電磁功率條件的大量匝數配合中熱負荷最小的一組匝數，可以稱為最優匝數，新舊匝數性能對比如表5所示。

表5 Y280電機新舊匝數性能對比

2 其他模型驗證

為驗證該方法對BDFM定子繞組匝數配合優化的普遍適用性，另對其他文獻[11-12]中的BDFM模型進行匝數優化及有限元仿真，電機模型基本參數如表6所示，有限元模型如圖5所示。匝數篩選過程及仿真模型設置類比Y280 BDFM模型，此處不再贅述。對于D400 BDFM，選出功率繞組和控制繞組的新匝數配合為36/192，具體性能對比如表7所示。

圖5 D400 BDFM有限元模型

表6 D400 BDFM模型基本參數

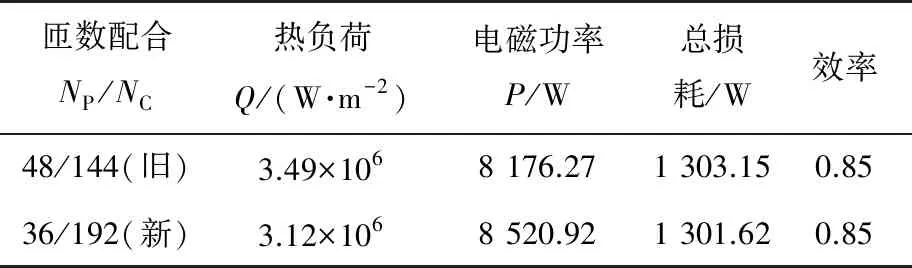
表7 D400 BDFM新舊匝數性能對比

3 匝數配合半解析優化流程圖

本文所述的BDFM定子繞組匝數配合優化的流程如圖6所示，具體可以分為以下四步。

圖6 匝數配合半解析優化流程圖

第一步：以最大功率不變為約束條件，通過式(18)得到所有滿足約束條件的匝數配合。

第二步：對滿足約束條件的多組匝數配合進行初步理論排除篩選，使其滿足1.3節的(1)(2)條件，且匝數配合結果應使電機在兩繞組共同激勵時能正常運行于雙饋同步狀態。

第三步：以電機熱負荷最小為優化目標，為避免解析誤差而導致漏失最優匝數配合，根據解析結果初步選出熱負荷前3組或前5組較小的匝數配合。

第四步：對篩選出的匝數配合進一步仿真，最終對比選出其中熱負荷仿真結果最小的一組，則該組匝數即為所有滿足功率約束條件中熱負荷最小的一組匝數配合。

4 結 語

本文提出了一種解析與仿真相結合的BDFM定子繞組匝數配合的半解析優化方法，以最大電磁功率不變為約束條件，以熱負荷最小為優化目標，對定子兩套繞組每相串聯匝數進行篩選和分析，最終針對Y280 BDFM室模型選出一組滿足功率約束條件且熱負荷最小的匝數配合：Np=108，Nc=480，并在其他BDFM模型上進行優化，驗證該方法對BDFM定子匝數優化的可行性與普遍適用性。本方法與完全依靠有限元仿真的匝數優化方法相比，顯著減少了仿真次數，縮短了優化設計周期并節約了大量的計算資源。