基于虛擬透鏡成像技術的轉臺ISAR成像方法

張繼龍，王 棟，張繼康

(1.蘇州威陌電子信息科技有限公司, 江蘇 蘇州 215312；2.中企基業(北京)管理顧問有限公司，北京 100039；3.北京敏視達雷達有限公司，北京 100094)

0 引言

在雷達技術基礎上進一步發展起來的合成孔徑雷達(synthetic aperture radar，SAR)[1-6]、逆合成孔徑雷達(inverse synthetic aperture radar，ISAR)[7-13]等技術近年來得到大量應用。其中SAR雷達通常位于運動平臺上，通過平臺運動在空間合成等效大口徑陣列而獲得更高的探測精度。而ISAR雷達則通常固定不動，通過目標的空間運動獲得等效的大口徑陣列來提高探測精度。在這兩種技術體制中，都需要目標與雷達平臺之間存在不同的相對運動以產生差異化的多普勒頻移，從而實現對目標的高精度探測。但由于實際雷達運載平臺或目標的運動都較為復雜，因而需要進行非常復雜的運動補償才能實現精確探測和成像。

虛擬透鏡成像技術[14-18]是一種成像新技術，即通過模擬透鏡成像機制，對陣列單元信號進行復加權運算，計算出預期成像平面上目標的像。文獻[14]首次提出了基于透鏡成像原理的微波陣列成像新思路，文獻[15]分析了成像特性，文獻[16]提出了一種快速成像算法提高了成像速度，文獻[17—18]解決了像場坐標修正等系列問題。虛擬透鏡成像技術具有算法簡潔高效、體制兼容性好的優點。本文在上述研究的基礎上，將該技術拓展到主動ISAR成像領域，提出一種ISAR轉臺成像新方法。該方法不依賴于目標回波的多普勒頻移，能夠實現對轉臺目標的高效成像。此外，本文所述方法同樣適用于圓柱掃描成像系統，也適用于柱面掃描合成孔徑雷達成像。

1 虛擬透鏡成像的基本原理

虛擬透鏡成像技術的基本原理如圖1所示，對天線單元接收到的目標散射信號移相后進行球面波二次散射，進而計算出在預定的成像平面上的合成像。

圖1 虛擬透鏡成像原理示意圖Fig.1 Schematic diagram of virtual lens imaging principle

文獻[17]給出了等效透鏡單元的移相量簡化計算公式及成像快速算法，其中移相量簡化計算公式為：

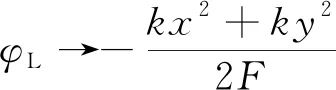
(1)

式(1)中，φL為陣列單元的透鏡相移，k為波數，(x,y)為天線單元坐標，F為焦距。

像場的快速計算公式為：

Eq=IFFT(E·A·ejφF)，

(2)

式(2)中，Eq為目標的像，E為陣列單元接收到的目標散射信號，A為陣列單元的幅度加權系數，φF為聚焦相位加權系數，符號IFFT代表二維快速傅里葉逆變換(IFFT)。

聚焦相位加權系數φF的計算公式如下：

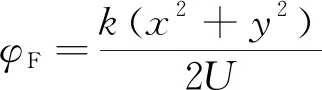
(3)

式(3)中，U為物距，即目標所在平面到陣列所在平面的距離。

2 新轉臺成像系統的特性

在傳統ISAR成像方法中，需要目標部件與雷達平臺之間存在不同的相對運動以獲得不同的多普勒頻移。將虛擬透鏡成像技術應用于ISAR成像，能夠實現不依賴于多普勒頻移的自聚焦成像。但現有虛擬透鏡成像技術是基于平面陣列天線，并且僅適用于被動式或半主動式成像，需要針對ISAR成像進行適應性改進。

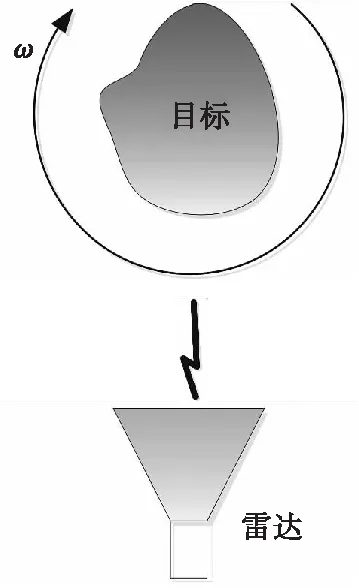
圖2 轉臺成像示意圖Fig.2 Diagram of turntable imaging

在圖2所示轉臺成像系統中，當探測雷達采用平行于轉動軸的一維線陣時，由于目標與探測雷達之間的相對運動，成像系統會形成圓柱面的空間合成陣面。在此圓柱面陣面探測系統中，目標散射信號傳輸到陣列單元，陣列單元收到信號進行移相后，以球面波的形式進行二次散射，信號傳播路徑如圖3所示。

信號經過不同的傳輸路徑R1、R2到達成像平面處，在不考慮傳播衰減的情況下，目標的像可用公式表示為[17]：

Eq(δ,σ)=Ep(ζ,ξ)?e-j(φ1+φL+φ2)dxdy,

(4)

式(4)中，Eq(δ,σ)為目標的像，Ep(ζ,ξ)為目標的散射信號，φ1為散射源P到陣列單元的單程傳播相移，φ2為陣列單元到像點Q處的單程傳播相移，φL為陣列單元的透鏡相移。

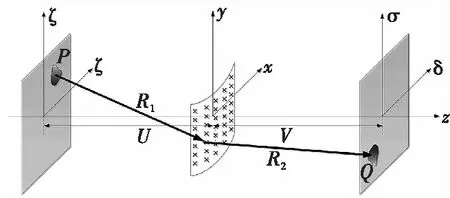
圖3 柱面成像示意圖及其坐標系Fig.3 Diagram of cylindrical imaging and its coordinate system

在柱坐標系下，假設目標位于柱面的軸線附近，柱面半徑為ρ,φ表示柱坐標系下，陣列單元偏離陣列中心的角度。(x,y,z)表示陣列單元的坐標，(ζ,ξ,-U)為散射源坐標，(δ,σ,V)為像點坐標；U為物距，即目標平面到陣列平面的距離；V為像距，即成像平面到陣列平面的距離；隨著掃描位置的變化，陣列單元的坐標存在如下關系式：

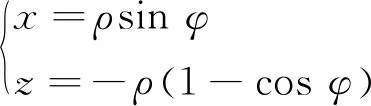
(5)

從而有：

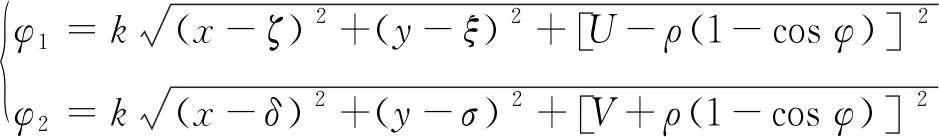
(6)

式(6)中，k為波數。

將式(6)級數展開并忽略高次項有：

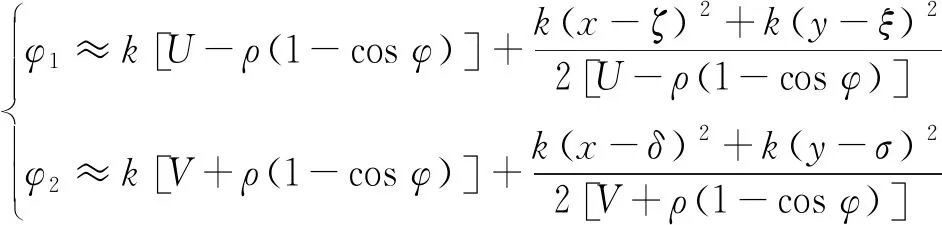
(7)

一般情況下，有U?ρ(1-cosφ)、V?ρ(1-cosφ)，從而式(7)可以進一步近似為：

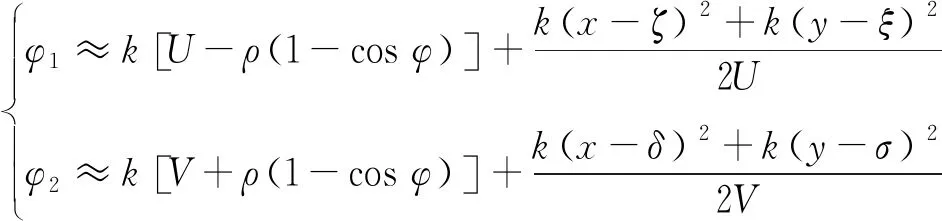
(8)

若僅考慮對成像有幫助的坐標相關變化分量，由式(8)還可以進一步得出成像有效相移為：

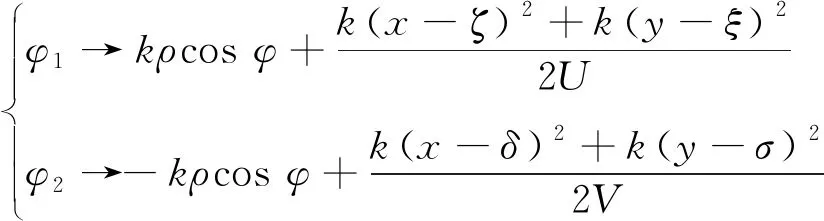
(9)

將式(1)、式(9)代入式(4)化簡整理可得：

Eq(δ,σ)=Ep(ζ,ξ)e-jψ1?e-jψ2ejωδxejωσydxdy，

(10)

式(10)中，

Eq(δ,σ)=Ep(ζ,ξ)·e-jψ1·?ejωδxejωσydxdy。

(11)

研究表明，陣面規模越大，式(11)右邊的二重積分結果越接近狄拉克函數(Dirac)的形態，此時所獲得的像與源場之間存在如下近似線性關系[17]:

(12)

通過分析同樣可以證明，虛擬透鏡成像技術也適用于主動式轉臺成像系統。主動ISAR轉臺成像系統中，在合成的虛擬柱面孔徑上，陣列單元依次發射和接收目標的反射信號，此時探測信號從天線單元發出，到目標反射后再被天線單元所接收，信號經歷了R1的雙程傳輸，對應的相位延遲為2φ1。在這種情況下，成像處理時則需要對透鏡單元相移、φ2傳播相移都作雙程處理。在不考慮傳播衰減的情況下，目標的像同樣可用公式表示為：

Eq(δ,σ)=Ep(ζ,ξ)?e-2j(φ1+φL+φ2)dxdy。

(13)

采用上述相似的推導過程，可證明式(12)同樣適用于主動式轉臺成像系統。

由上述分析可知，虛擬透鏡成像技術可用于轉臺成像系統，且所成的像與源之間存在良好的近似線性關系，并且該成像方法可不依賴于多普勒頻移。

3 轉臺ISAR成像快速算法

前面已經證明虛擬透鏡成像技術可用于轉臺ISAR成像，下面將給出成像算法的實現模型。

由于實際合成的虛擬柱面通常為離散陣列，假設陣列單元接收到的目標信號為E，成像時需要對陣列接收到的信號作如下處理：

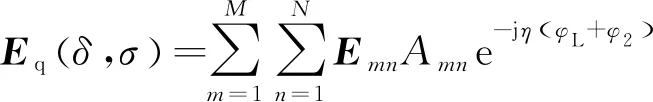
(14)

式(14)中，Emn為陣列單元接收到的場，Amn為陣列單元的幅度加權系數。參數η與成像系統的特性相關，η=1，可適用于被動式ISAR轉臺成像系統；η=2，可適用于主動式ISAR轉臺成像系統。

將式(1)、式(9)代入式(14)，化簡整理后得：

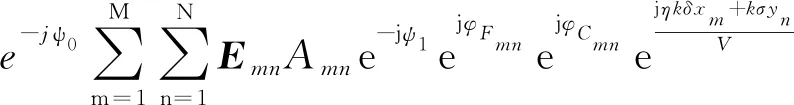
(15)

式(15)中，

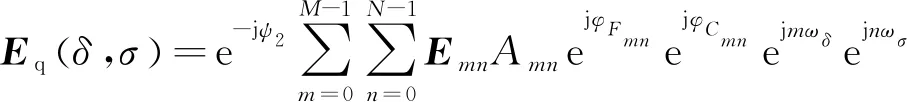
(16)

式(16)右邊的系數滿足|e-jψ2|=1，反映了像場的空間波動特性，對成像基本無影響，可忽略。求和運算則可用二維IFFT進行快速求解，則像場計算公式可簡化為：

Eq(ωδ,ωσ)=IFFT(E·A·ejφFejφC)。

(17)

對比式(17)給出的轉臺成像快速算法與文獻[17]算法可知，二者的差異在于轉臺成像公式中增加了一項相位補償因子φC，該補償因子與等效柱面半徑ρ以及陣列單元偏離陣列中心的角度φ有關。

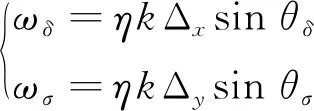
(18)

式(18)中，θδ、θσ為像點掃描角坐標，從而可得出像點角坐標計算公式為：

(19)

在轉臺成像系統中，目標往往位于合成虛擬柱面的軸線附近，此時需要用目標到局部柱面陣列中心的斜距R代替物距參數U。聚焦相位補償因子φFmn的計算公式為：

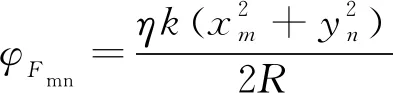
(20)

當轉臺系統的旋轉角速度為ω時，令φ=ωt，t為時間，取位于合成的虛擬柱面中心的時刻為零。式(17)快速算法對應的相位加權系數可改寫為：

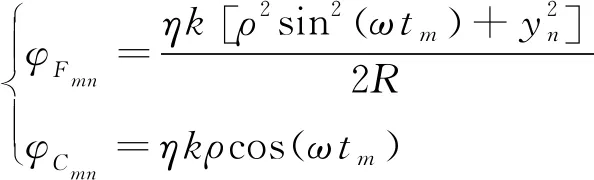
(21)

只要能夠獲得較為準確的目標距離參數R，采用式(21)進行配相，本文所述成像算法能夠實現自動聚焦成像。相比傳統ISAR成像算法，新算法更為簡潔。

由式(17)、式(21)可知，本文給出的快速成像算法，采用了“幅相加權+IFFT”的技術體制，僅需進行一次IFFT快速運算即可獲得目標的像，相比傳統轉臺成像算法，大幅降低了運算量。

4 成像驗證

采用電磁場仿真軟件(如Feko、CST等)進行仿真，構造“R”形金屬目標，其高0.4 m，寬約0.32 m。先進行被動成像仿真，用平面波對“R”形金屬目標進行照射，計算轉臺成像所形成的虛擬圓柱陣面上的散射場分布，電磁仿真的示意圖見圖4(a)。系統工作頻率為10 GHz，圓柱半徑為1 m，柱面高度2 m，單元間距為半波長，“R”字形目標位于圓柱軸線上。通過電磁仿真獲得的柱面上的場分布見圖4(b)。

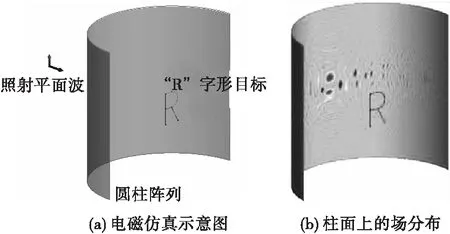
圖4 被動成像電磁仿真及目標回波分布Fig.4 Passive imaging electromagnetic simulation and target echo distribution

對電磁仿真獲得的柱面場分布數據進行處理，編寫成像計算程序，取參數η=1，成像結果見圖5，在所成的像中能夠清晰分辨出“R”字形目標。

圖5 被動式轉臺成像仿真結果Fig.5 Simulation results of passive turntable imaging

隨后進行主動成像仿真，模擬豎直放置的一維線陣主動式轉臺成像，目標同樣為“R”形金屬目標。實際仿真時采用方位全向的偶極子天線探測目標，將該偶極子天線依次放置在轉臺成像所形成的虛擬圓柱陣面上的不同陣列單元的位置，計算天線饋電端口的s11參數，電磁仿真的示意圖見圖6(a)。系統工作頻率為10 GHz，圓柱半徑為1 m，柱面高度2 m，單元間距為四分之一波長，“R”字形目標位于圓柱軸線上。通過電磁仿真獲得的目標散射場分布見圖6(b)。

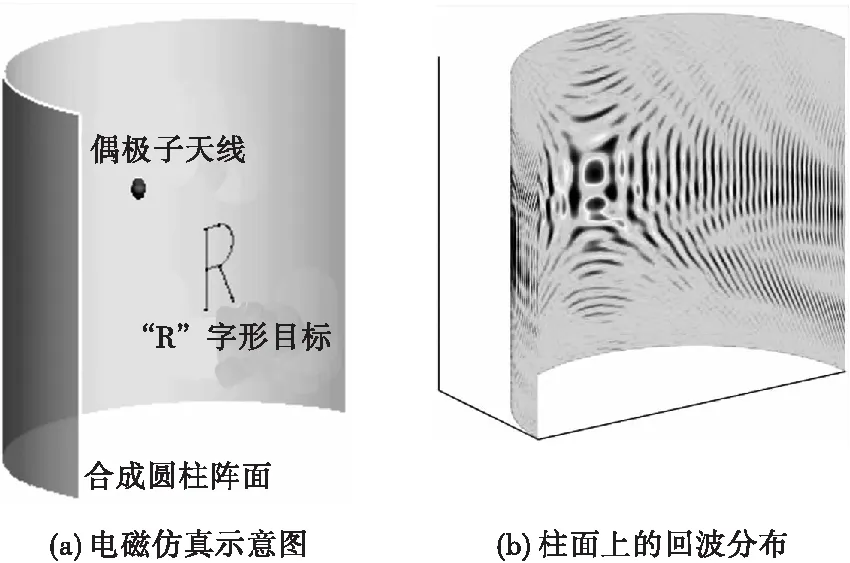
圖6 主動成像電磁仿真及目標回波分布Fig.6 Active imaging electromagnetic simulation and target echo distribution

對電磁仿真獲得的柱面場分布數據進行處理，編寫成像計算程序，取參數η=2，成像結果見圖7，在所成的像中能夠清晰分辨出“R”字形目標。

圖7 主動式轉臺成像仿真結果Fig.7 Simulation results of active turntable imaging

5 結論

本文提出一種不依賴于多普勒頻移的ISAR成像新方法，該方法既適用于被動成像又可用于主動成像系統。此外，本文所述方法同樣適用于圓柱掃描成像系統，也適用于柱面掃描合成孔徑雷達成像。相比傳統ISAR轉臺成像方法，該方法大幅降低了運算量，提高了成像速度，降低了硬件成本，具有重大的工程應用價值。