不同排澇情景下泵站單機組變角優化運行研究

陶旭輝，仇錦先，闞永庚

（1.揚州大學水利科學與工程學院，江蘇揚州 225009；2.江都水利工程管理處，江蘇揚州 225200）

0 引 言

近年來，由于氣候異常引起的自然災害頻繁發生，特別是短歷時暴雨或持續性降水往往引起洪澇災害［1，2］。若區域性澇水不及時排出，則會對當地的生產、生活和生命財產安全造成危害或損失。據統計，暴雨洪澇損失約占全球各種自然災害損失的40%［3］。而排澇泵站是區域澇水及時排出的重要設施，如何提高汛期排澇泵站排水效率或節省耗能，已引起國內外學者的關注，并開展了相關理論研究與應用。

Fecarotta 等［4］構建了排澇泵站能耗最小的混合整數優化模型，并應用于意大利那不勒斯城市排水系統，平均節省32%的能耗；Yazdi 等［5］考慮降雨事件的隨機性，通過耦合一個數學模型和一種新的混合和聲搜索算法，獲得了排澇泵站最優運行策略，并應用于實際城市排水系統，有效提高了排水效率。袁丹青等［6］構建了以全年排澇耗能最小為目標、以受澇時間和澇水位為約束的數學模型，實現了排澇泵站的最優調度；張禮華等［7，8］分別構建了以開機機組總耗能最少和能耗率最低為目標，以及機組運行費用最少為目標的優化模型，實現了特定排水標準下的排澇泵站最優運行；吳遠為等［9］構建了以耗電量最低為目標、以排水量和功率等為約束的站內優化調度模型，得到了排澇泵站較好的優化調度方案；劉靜森等［10，11］提出排澇泵站群總能耗最小的多方案試驗選優、圩區外河水位控制去劣的優化運行調度方法，有效降低了城鎮圩區排澇泵站群日常運行能耗；高玉琴等［12］構建了圩區排澇泵站等功耗下排水量最大的優化調度模型，有效提高了排澇泵站除澇效率；張浩等［13］以排澇效果最佳為目標，通過多機多種運行模式組合數值模擬，獲得了排澇效果最佳、河道和航運安全影響最小的運行方案。

上述研究數學模型大部分是以排澇泵站耗能最小或排水量最大為單目標的優化問題，本文針對不同排澇標準（日常排澇、超標準排澇）、不同排澇階段（預降階段、搶排階段）等實際情況，擬構建綜合考慮排水量最大、耗電費用最小的多目標優化數學模型。同時，考慮到泵站機組不宜頻繁啟停，所以在優化模型中擬增加文獻尚不多見的停機次數作為約束條件，以期最終的優化結果更具有可操作性，更符合排澇泵站實際運行情況。

1 優化模型構建與求解

1.1 目標函數

針對變角運行的排澇泵站單機組，考慮汛期不同排澇標準、不同排澇階段的實際要求，以規定時間內排水量最大、耗電費用最低為多目標函數，以機組運行功率、葉片安放角度、停機次數等為約束條件，構建綜合考慮排水量和耗電費用的非線性多目標排澇泵站單機組變角優化數學模型。

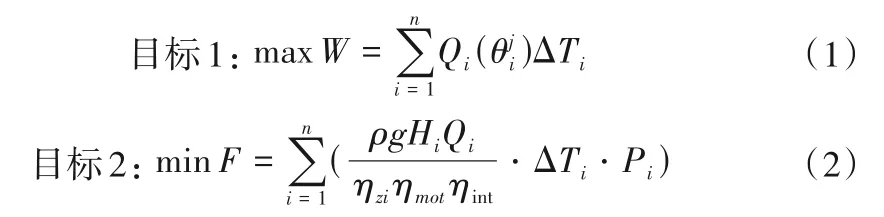
式中：W 表示一個排澇周期內最大排水總量，萬m3；i表示時段，i=1，2，…，n（時段總數）；θij表示第i 時段第j 個葉片角度離散取值表示第i 階段第j 個角度所對應的排澇流量，m3/s，揚程一定時其是θij的函數，不開機時為0；ΔTi為第i 時段時間長度，h；F為一個排澇周期內耗電費用，元；Hi為第i時段平均排澇揚程，m；Pi為第i時段分時電價，元（/kWh）；ηzi、ηmot、ηint分別表示第i 時段泵裝置效率（根據泵裝置Q～η 性能曲線確定）、電動機效率和傳動效率。

1.2 約束條件

（1）葉片安放角度約束。

式中：θmin、、θmax分別表示葉片安放角度的最小值與最大值。

（2）運行功率約束。

式中：Ni(θi)表示第i 時段機組實際運行功率，kW；Ne表示機組電機額定功率，kW。

（3）停機次數約束。

式中：u、umax分別表示一個排澇周期內機組運行實際停機次數和允許最大停機次數。

1.3 模型求解

上述構建的兩個目標函數（排水量最大、耗電費用最小）存在一定的矛盾沖突，而當各個目標函數處于沖突狀態時，就不會存在使所有目標函數同時達到最大或最小值的最優解，通常只能尋求一組非劣解。為了求得多目標規劃問題的非劣解，又常常需要將多目標規劃問題轉化為單目標問題去處理。文獻［14］也提出“在多目標優化的情況下，特別是當各個目標之間有矛盾沖突時，可以先控制一些目標然后使另一個目標達到最大（最小）化”。因此，考慮到排澇泵站兩目標重要程度不同（抓住主要目標、兼顧次要目標），選擇排水量最大作為主要目標，而耗電費用最小只要滿足一定的控制要求，將其轉換成約束條件，即將多目標優化模型轉化如下單目標優化模型求解：

為得到一系列不同耗電費用下各時段決策方案及最大排水量，供泵站管理部門在不同排澇情景下決策參考，這里采用一維動態規劃法［14］進行模型的求解。以時段作為階段變量，以葉片安放角度作為決策變量，以耗電費用作為狀態變量，各階段狀態轉移方程、系統遞推方程如下：

（1）階段i=1：

狀態變量λ1在其可行域［f1，1，f1，m］內離散：λ1= f1，1，f1，2，f1，3，…，f1，m，其中f1，1、f1，m分別表示第1 階段開機時的最小費用與最大費用；m表示按等步長離散的個數。

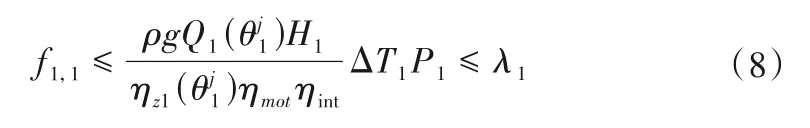
（2）階段i（1＜i ＜n）：

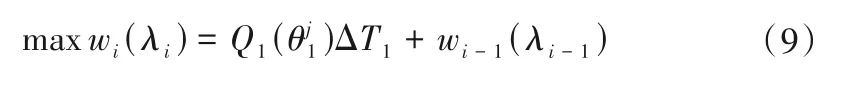
狀態變量λi在其可行域［fi，1，fi，m］內離散：λi= fi，1，fi，2，fi，3，…，fi，m，其中fi，1表示第1～i 階段均開機時的各階段最小費用中的最小值；fi，m表示第1～i 階段均開機時的各階段最大費用之和。

狀態轉移方程：

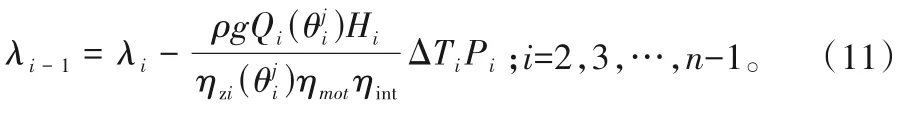
（3）階段n：

狀態變量λn在其可行域［fn，1，fn，m］內離散：λn=fn，1，fn，2，fn，3，…，fn，m，其中fn，1表示n 個階段均開機時的各階段最小費用中的最小值；fn，m表示n個階段均開機時的各階段最大費用之和。

狀態轉移方程：

2 實例應用與計算結果分析

本文選取某圩區排澇泵站單機組變角優化運行為例，建立以日運行排水量最大和耗電費用最小為多目標的數學模型，采用上述一維動態規劃算法、同時輔以Frotran 語言編程求解，可以得到一系列與不同耗電費用所對應的運行方案，包括各時段開停機、葉片安放角度的決策情況，以及一日最大排水量、實際耗電費用和單位費用排水量（即最大排水量除以實際耗電費用，m3/元）。

2.1 基本參數說明與確定

（1）時段劃分與分時電價。根據汛期排澇泵站一天內揚程變化情況，結合江蘇省峰谷電價時段劃分，將一天劃分為9個計算時段。具體時段劃分與分時電價見表1。

表1 各時段內平均揚程及分時電價Tab.1 Average head and time-of-use price in each period

（2）時段內平均揚程。該圩區汛期警戒水位為2.0 m，根據圩區多年汛期排澇運行情況，當內河水位上升到1.8 m，且天氣預報仍有強降雨過程，則開機排澇預降水位，圩區內河水位一般呈現先降、后升再降的變化過程，而外河水位相對變化不大（一般6.2 m 左右）。以該圩區某一設計頻率的來水過程為例，排澇泵站一天內不同時段平均揚程如表1所示。

（3）流量和裝置效率。排澇泵站的機組型號為2000ZLQ1 3.7-7.8，額定轉速為214.3 r/min，設計葉片角度為+2°。在排澇泵站變角運行情況下，根據水泵不同葉片安放角度（-6°、-4°、-2°、0°、+2°、+4°）時的Q～H、Q～η性能曲線，結合時段平均揚程，可確定各時段不同角度時的排澇流量和裝置效率［15］。

2.2 計算結果分析

大型泵站不宜頻繁停機，否則會縮短機組使用年限，增加設備維修費用，甚至危及泵站運行安全。本文考慮停機次數對變角優化運行結果的影響，分別分析無停機約束、停機次數0次約束和1 次約束3 種情況下，不同耗電費用下的最大排水量及單位費用排水量變化規律，見圖1～3。其中，超標準排水或搶排階段以不停機考慮，即停機次數為0；預降階段考慮停機次數不超過1次；日常排水不考慮停機次數約束。

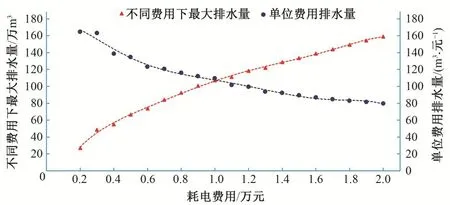
圖1 無停機次數約束下最大排水量及單位費用排水量變化情況Fig.1 The variation of maximum drainage and unit cost drainage（not considering the constraint of shutdown times）

（1）無停機次數約束下最大排水量及單位費用排水量變化情況如圖1 所示。由圖1 可知，不同耗電費用下的最大排水量總體上呈上升趨勢，其中耗電費用0.2～1.0 萬元（最大耗電費用的10%～50%）區間上升趨勢較為明顯，即增加相同數量費用，提水量增加幅度較大；耗電費用1～2 萬元（最大耗電費用的50%～100%）區間最大排水量上升幅度減緩，曲線較為平緩。另外，不同耗電費用下的單位費用排水量曲線總體呈下降趨勢，以耗電費用1 萬元（最大耗電費用的50%）為界，右邊單位費用排水量曲線段下降較為平緩，而左邊曲線段下降較快，這表明在低費用階段（小于最大耗電費用的50%），排水總量雖然處于較低水平，但單位費用排水量處于較優的狀態，即單位費用可排出較多的水量，這適用于排水量不多、兼顧節省能耗的日常排水。

（2）在不停機（停機次數為0）約束下最大排水量及單位費用排水量變化情況如圖2所示。當圩區發生超標準降水或內河水位超出警戒水位，排澇泵站投入搶排階段，此時機組考慮不停機而連續運行，使內河水位盡快降至安全水位，以保證區域免受澇災。本實例當機組一天內不停機時最低耗電費用為14 861.0 元，故這里選取耗電費用1.5～2.0 萬元作為分析區間。由圖2可知，最大排水量隨耗電費用增加而增加，但增加的幅度表現為曲線先陡后緩；這從單位費用排水量曲線也可以看出，耗電費用1.50～1.65 萬元區間單位費用排水量呈上升趨勢，而1.65～2.00 萬元區間呈下降趨勢。同時，耗電費用1.6～1.7 萬元（最大耗電費用的80%～85%）區間單位費用排水量較大，是多目標（提水量盡可能多、耗電費用盡可能少）均較優的區間，此區間最大排水量約為耗電費用2 萬元時最大排水量的85%～90%。

圖2 不停機約束下最大排水量及單位費用排水量變化情況Fig.2 The variation of maximum drainage and unit cost drainage（considering the constraint of“shutdown times”=0）

（3）根據無停機約束條件下不同耗電費用下最大排水量的計算結果可知，一個排澇周期內間斷性的停機次數一般不超過2次（這里指不相鄰的階段停機次數累加值，若計算中出現相鄰階段連續停機，則停機次數按1 次考慮），結合排澇泵站運行的實際情況，將停機次數約束取1 次為宜。由圖3 不同費用下最大排水量曲線可以看出，總體上最大排水量隨耗電費用增加而呈上升趨勢。當耗電費用在0.6～1.2 萬元（最大耗電費用的30%～60%）區間時，由程序計算結果可知，無停機約束時停機次數超過1 次（如表2 所示），而考慮停機次數約束時，因受停機次數≤1影響，在動態規劃尋找最優路徑時需作出調整。從圖中趨勢線水平段可以看出，受約束條件影響耗電費用在此區間時的實際耗電費用和最大排水量均與0.6 萬元時一致。另外，單位費用排水量曲線總體上則呈下降趨勢，同樣受停機次數約束影響中間段曲線呈水平趨勢。因此，當耗電費用有保證且排澇處于預降階段時，考慮停機次數≤1 的約束條件，建議在耗電費用1.2～2.0 萬元（最大耗電費用的60%～100%）區間變角優化運行，此時可獲得較多的排澇水量。

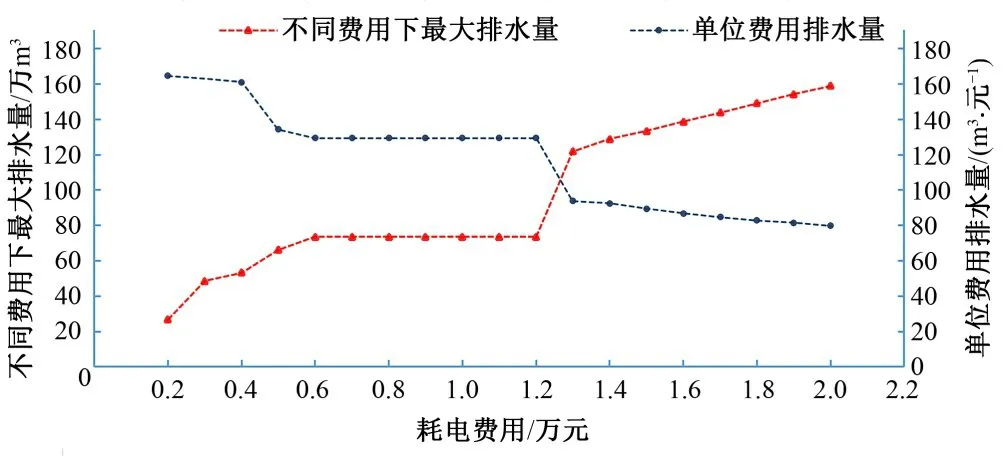
圖3 停機次數≤1約束下最大排水量及單位費用排水量變化情況Fig.3 The variation of maximum drainage and unit cost drainage（considering the constraint of“shutdown times”≤1）

表2 停機次數對優化結果的影響（以耗電費用≤6 000元為例）Tab.2 Influence of shutdown times on optimization results（taking“power consumption cost”≤6 000 yuan as an example）

3 結 論

本文綜合考慮排澇泵站的排水量與耗電費用，構建了非線性多目標單機組變角優化數學模型，選取某排澇泵站日運行為例，分析了單機組在不同排澇情景下的計算結果，并對汛期排澇泵站優化運行提出了建議。主要結論與補充說明如下：

（1）根據無停機次數約束下變角優化運行最大排水量及單位費用排水量分析，當給定耗電費用小于最大耗電費用的50%，排水總量雖然處于較低水平，但單位費用排水量處于較優狀態，即單位費用可排較多水量，這適用于排水量不多、且考慮能耗節省的日常排澇。

（2）根據不停機約束下變角優化運行最大排水量及單位費用排水量分析，當給定耗電費用在最大耗電費用的80%～85%區間時單位費用排水量較大，且排水量約為最高費用所對應的最大排水量的85%～90%，是排水總量、耗電費用均較優的區間，這適用于不考慮停機而連續運行的超標準排澇或搶排階段。

（3）根據停機次數≤1約束下變角優化運行最大排水量及單位費用排水量分析，當耗電費用有保證時，且排澇處于預降水位階段，可考慮停機次數≤1 的約束條件，并建議在最大耗電費用的60%～100%區間變角優化運行，可以保證較多的排水總量。

（4）實例得到了一系列與不同耗電費用所對應的各時段開停機、葉片安放角度的決策方案，以及相應的最大排水量。在實際應用時，可根據不同排澇情景下預估的排水量，選擇相應的決策方案。

（5）構建的數學模型適用于單機組變角優化運行問題，若是多機組變角優化運行，在模型中還要增加開機臺數這一決策變量。關于多機組排澇泵站變角優化問題，將作為后續進一步開展研究的內容。