輪對非線性動力學系統蛇行運動的解析解1)

史禾慕 曾曉輝 ,* 吳 晗

* (中國科學院力學研究所流固耦合系統力學重點實驗室,北京 100190)

? (中國科學院大學工程科學學院,北京 100049)

** (大連理工大學海岸和近海工程國家重點實驗室,遼寧大連 116024)

引言

鐵路車輛蛇行動力學響應特性是列車設計和運營中的關鍵問題,國內外學者對此進行了大量研究.關于整車系統動力學的分析大都采用數值方法.Schupp[1]將基于路徑跟蹤法的分岔分析軟件和Simpack 多體動力仿真軟件相結合研究系統的分岔特性,計算了車輛系統的極限環.Cheng 等[2-3]研究了車輛系統的不同參數對于臨界速度的影響規律.文獻[4-5]等研究了車輛系統的分岔特性,計算了車輛系統的分岔圖和極限環等.文獻[6]分別采用路徑跟隨(path-following)方法和蠻力(brute-force)方法研究了鐵路客車的分岔和蛇行運動特性.True[7]對于幾種求解車輛系統非線性臨界速度的方法進行了分析,并給出了求解非線性速度的正確方法.Iwnicki等[8]總結了鐵路貨車的發展歷史,研究了幾種常見鐵路貨車的動力學特性.翟婉明[9]提出了車輛-軌道耦合動力學理論,使得理論研究更能反應鐵路輪軌系統實際情況,對于軌道類型對車輛系統的臨界速度影響進行了廣泛研究.曾京[10]采用QR 算法和黃金分割法計算了17 自由度經典客車模型的線性臨界速度,采用打靶法計算了其鄰域的極限環.羅仁和曾京[11]的研究表明,在研究列車系統蛇行運動穩定性時,采用單節車模型計算得到的臨界速度與多編組列車的臨界速度相差很小.高學軍等[12-13]采用延續算法計算了車輛系統的周期解,研究了車輛系統的分岔和混沌現象.Zeng 等[14-19]綜合考慮了氣動載荷對車輛動力學系統固有特性的影響以及強迫激勵的作用,給出了氣動載荷作用下車輛系統動力學響應特性分析方法,分析了相關參數的影響規律.

上述對整車動力學系統進行研究更接近實際情況,也搞清楚了一些作用機理.盡管如此,目前仍然有一些問題的內在機制不很清楚.部分原因是,整車系統自由度較多、可變參數也多,各參數對蛇行穩定性影響的效應交織在一起,不易分清各種因素的貢獻大小,也就不容易更深刻理解為什么會有這樣的影響規律.這種狀況并不利于高效地改進工程設計.

輪對系統保留了影響車輛系統動力學性能的幾個關鍵的要素:輪軌幾何非線性約束、輪軌接觸蠕滑關系、懸掛系統等.從蛇行穩定性問題的角度來說,輪對系統也是能從相當程度上代表整車系統蛇行穩定性特性的典型子系統.而且,輪對系統自由度少、參數少,可以采用解析方法進行分析,便于更深入地認識車輛動力響應特性及內在機理.目前國內外學者針對輪對系統也開展了相關研究.

Wagner[20]計算了具有亞臨界霍普夫分岔的鐵路輪對系統的兩個穩定解的吸引域,并給出兩個穩定解出現的概率.Casanueva 等[21]建立了考慮輪對柔性的輪對動態穩定性模型,分析了輪對參數對于臨界速度的影響規律.Antali 等[22-23]推導了圓錐車輪在圓柱軌道的精確非線性方程,研究了鐵路輪對的運動特性.Song 等[24]建立了1/5 輪對比例模型,通過實驗和數值研究了車輪踏面錐度對于橫向動力學特性的影響.Pascal 和Sany[25]建立了考慮輪軌共形接觸的獨立輪對動力學模型并研究了其動力學特性.文獻[26]研究了具有三次和五次非線性的輪對動力學方程的亞臨界霍普夫分岔和鞍結分岔,并通過實驗進行了驗證.文獻[27]研究了輪對系統在兩分岔參數下的分岔行為.Ge 等[28]建立了具有非線性等效錐度和輪軌力的修正鐵路輪對動力學模型,并對其失穩機理進行了研究.Guo 等[29]建立了考慮輪軌接觸非線性的鐵路車輛輪對動力學模型,并對其分岔特性進行了研究.武世江等[30]對考慮陀螺效應的輪對系統的霍普夫分岔特性進行了研究,給出了線性臨界速度表達式,基于打靶法計算了輪對系統的分岔圖.

本文采用解析方法對輪對系統的蛇行運動穩定性問題開展研究.推導出帶有小參數的兩自由度方程,并采用多尺度方法[31]進行解析求解;給出輪對系統極限環幅值的解析表達式并對其穩定性進行判定;給出了輪對系統非線性臨界速度的解析表達式.將所獲得的解析解與數值結果進行對比,驗證了解析解的正確性.采用得到的解析解進行了參數影響分析.

1 輪對動力學建模

1.1 模型概述

輪對系統是鐵路車輛動力學系統中最關鍵的部分,它包含懸掛系統以及兩個通過車軸連在一起的車輪(稱為輪對).一系懸掛系統將輪對和轉向架構架連接起來;輪對受鋼軌約束,在鋼軌上無跳躍地運動.輪對系統示意圖如圖1 所示.

圖1 輪對模型示意圖Fig.1 Schematic diagram of the wheelset model

在上述輪對系統中,轉向架構架沿水平方向勻速前進,輪對沿著軌距不變、剛性路基的平直軌道運動.輪對和構架之間由一系懸掛彈簧連接.車輪與鋼軌永保接觸,由此輪對的垂向和側滾位移與其橫擺和搖頭位移相關聯,于是考慮模型有橫擺y和搖頭ψ兩個自由度,車輪和鋼軌間的蠕滑符合線性規律,不考慮自旋蠕滑的影響.系統的非線性來自于輪軌接觸非線性回復力.

1.2 輪對動力學方程

通過牛頓-歐拉法推導輪對動力學方程如下所示

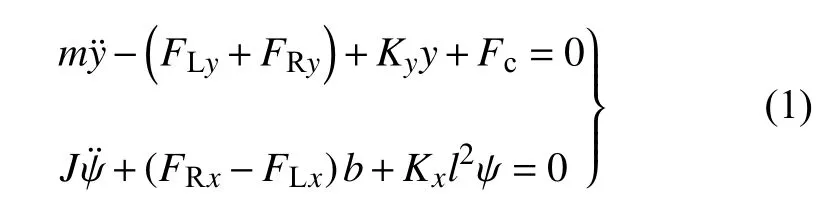
式中,m是輪對的質量,J是輪對相對于垂直軸的搖頭轉動慣量,FLx和FLy是左側車輪的縱向和橫向蠕滑力,FRx和FRy是右側車輪的縱向和橫向蠕滑力,Kx和Ky是一系懸掛縱向、橫向彈簧總剛度.Fc代表由軸重和輪軌幾何關系引起的橫向復原力,b是名義滾動圓距離之半,l是一系懸掛橫向距離之半.

本文中采用卡爾克(Kalker)線性蠕滑理論計算輪軌接觸蠕滑力[20,27-28,30,32-33],如下

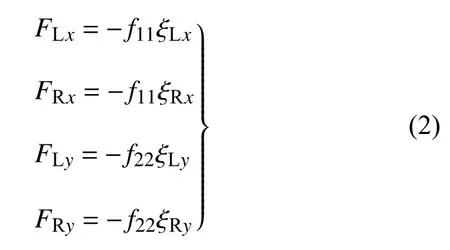
式中,f11和f22是車輪的縱向、橫向蠕滑系數,ξLx和ξLy是左側車輪的縱向、橫向蠕滑率,ξRx和ξRy是右側車輪的縱向、橫向蠕滑率,具體表達式如下

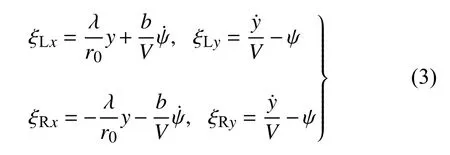
式中,λ是等效錐度,r0是名義滾動圓半徑,V是輪對運行速度.

車輛動力學中輪軌接觸恢復力通常由輪軌接觸幾何和輪對軸重決定,表達式如下

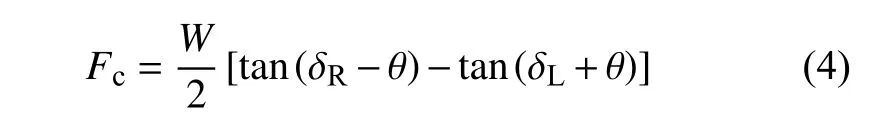
式中,W是軸重,δL和δR是左、右車輪接觸角,θ是輪對側滾角.對于LMA 型車輪踏面和CHN60 型鋼軌接觸配合,接觸幾何參數tan(δR-θ)-tan(δL+θ)隨輪對橫擺的變化關系可用多項式函數擬合,如圖2所示.

圖2 tan(δR-θ)-tan(δL+θ)隨輪對橫擺變化關系Fig.2 tan(δR-θ)-tan(δL+θ)varies with the lateral displacement of wheelset

具體的擬合公式如下

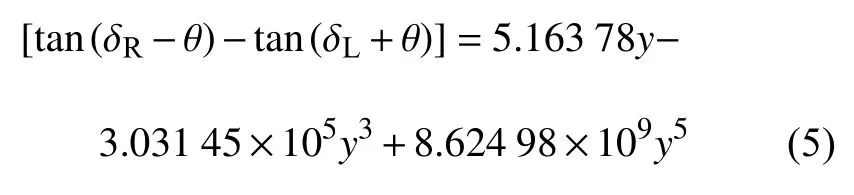
將式(5)代入式(4)有

式中δ0,δ1和δ2是關于輪軌接觸橫向復原力的多項式擬合函數的系數.

將式(2)～式(6)代入式(1),重寫輪對動力學表達式如下

方程(7)中各符號參數的取值參見附錄A 中的表A1.

由于方程(7)帶有三次和五次非線性,很難得到其精確解,于是考慮采用攝動法求解其近似解析解.

為采用多尺度方法求解如式(7)所示的非線性方程,首先選擇合適的特征量對動力學方程進行無量綱化,把式(7)變為帶有小參數的無量綱方程,如式(8)所示

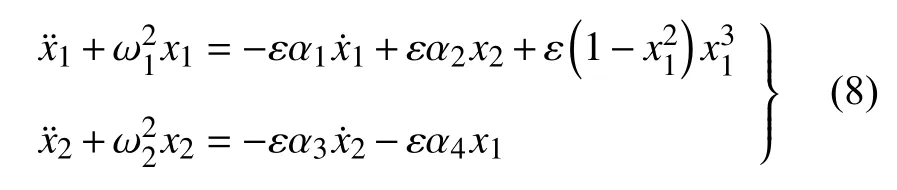
式中

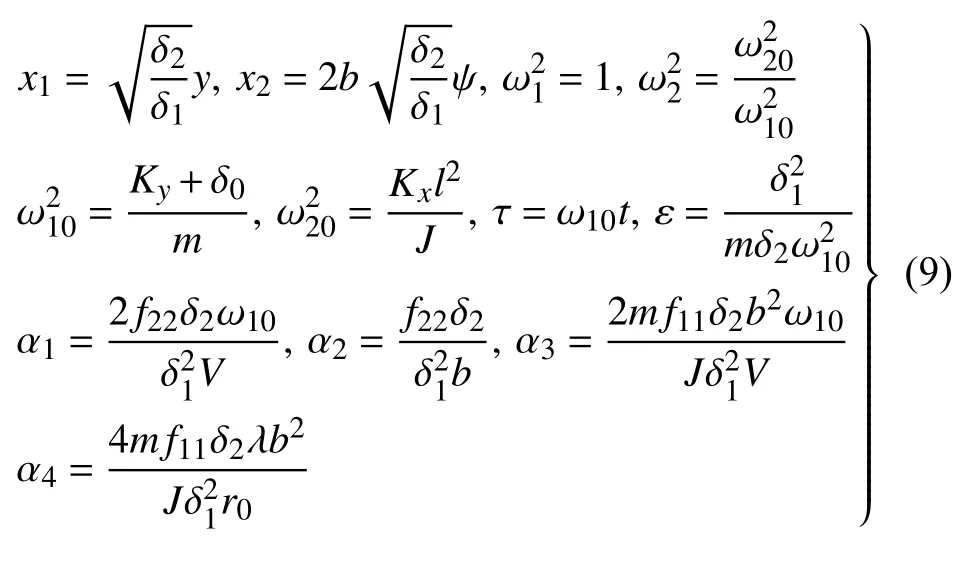
對于目前常用的輪軌外形(LMA 型車輪踏面和CHN60 型鋼軌)和剛度[20,28]等參數進行計算,式(8)中非線性項的系數ε約0.1,此時無量綱化的動力學方程(8)可以采用多尺度方法進行求解.

2 多尺度法求解輪對動力學方程

本節給出基于多尺度方法的方程(8)的一階解析解.

設方程(8)的解的形式

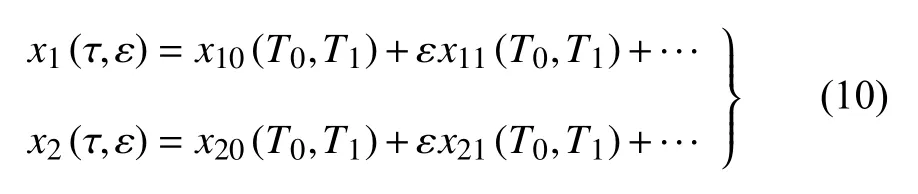
式中Tn=εnτ(n=0,1,2,···),于是對時間的微分可表示為如下形式

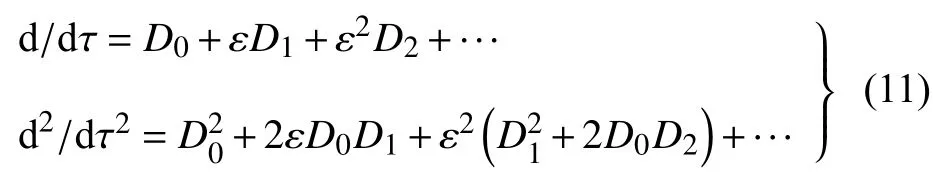
將式(10)和式(11)代入方程(8),并令兩端ε0和ε1的系數分別相等,得到

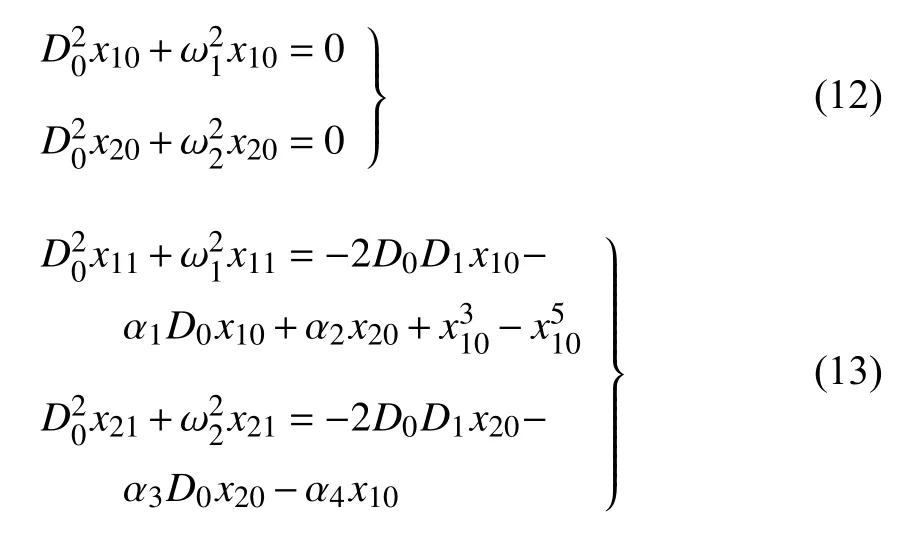
方程(12)的解可寫成如下形式

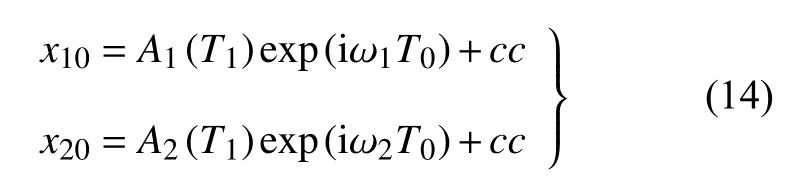
式中An(n=1,2)為待定復函數,cc表示左邊各項的共軛復數.

將式(14)代入方程(13)有

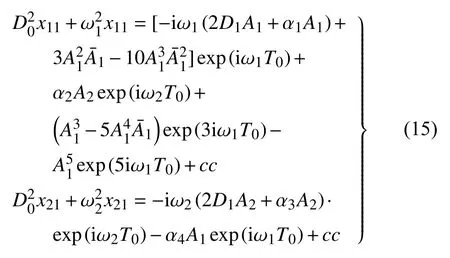
式中橫線代表該函數的共軛復數.為避免久期項的存在,函數An(n=1,2)需滿足以下方程

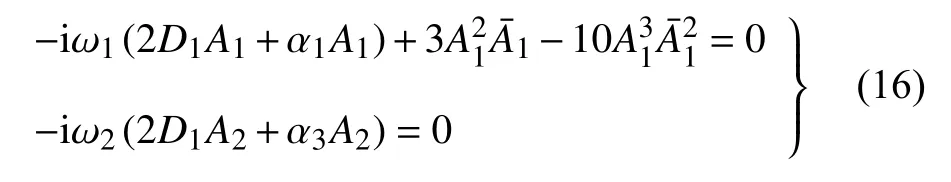
在上式中將An(n=1,2)寫成指數形式

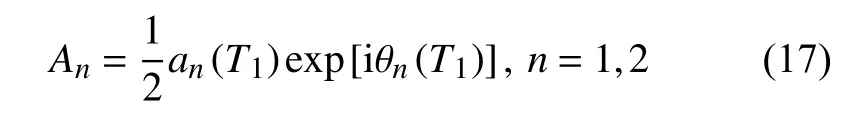
式中an和θn(n=1,2)都是實數,將式(17)代入式(16),并分離實部和虛部,得到

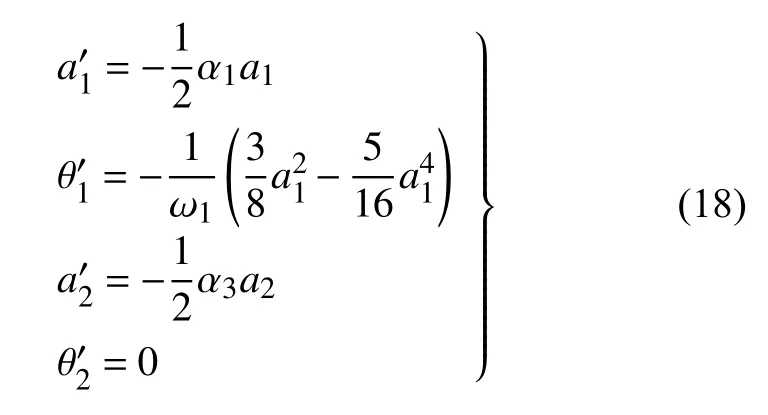
式中,一撇代表對T1求導數.對上式積分可以得到

眾所周知,鐵路輪對動力系統是一個自激振動系統,當運行速度超過臨界速度后,系統會出現蛇行失穩導致蛇行運動振幅不再衰減,此時蛇行運動的振幅和頻率與運行速度相關.工程實際中,式(19)中參數α1和α3總是正數,因此無論速度如何變化,隨著時間的增加,系統蛇行運動幅值a1和a2總是趨近于零.這顯然與實際情況不符.實際上在這里需要考慮系統的內共振的影響.由于輪對的蛇行運動是輪對的橫擺和搖頭相耦合的運動,通過內共振可以將輪對的橫擺和搖頭運動結合起來,這一點也是符合實際意義的.下面給出考慮內共振時方程的解.

對于系統的內共振情況,引入解諧參數σ1來表示頻率ω1和ω2的接近程度，即

將上式代入式(15),為避免久期項的存在,函數An(n=1,2)需滿足以下方程

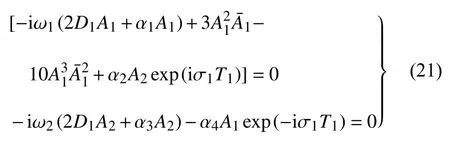
將式(17)代入上式,分離實部和虛部有

可見,系統總有零解,當系統的幅值(a1,a2)不為零時,引入

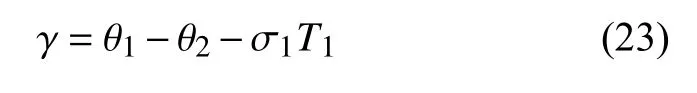
利用上式將式(22)化為自治形式

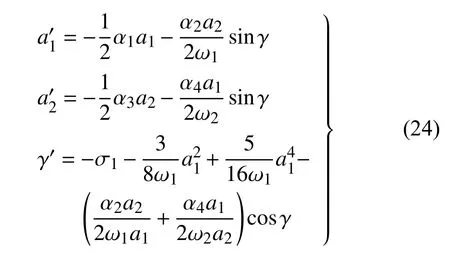
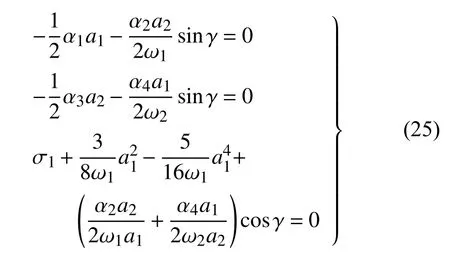
由方程組(25)中前兩式可得

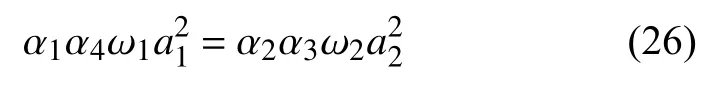
在這里考慮穩態幅值均為正,由式(26)可得

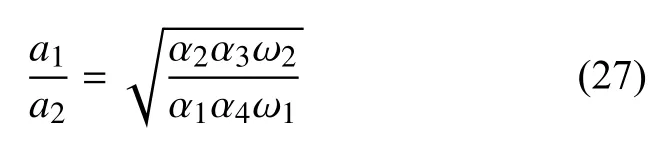
將上式代入方程組(25)中第二式有

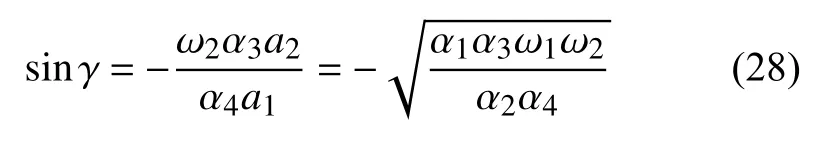
利用三角恒等式 cos2γ+sin2γ=1,有

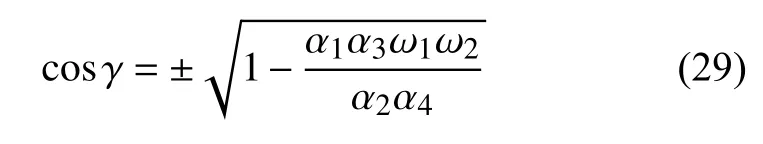
將上式和式(27)代入方程組(25)中第三式,化簡有

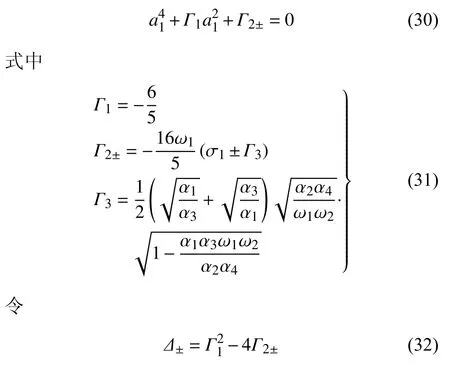
由于 Γ1＜0,需要分情況討論

(1)Δ±≥0,Γ2±≥0

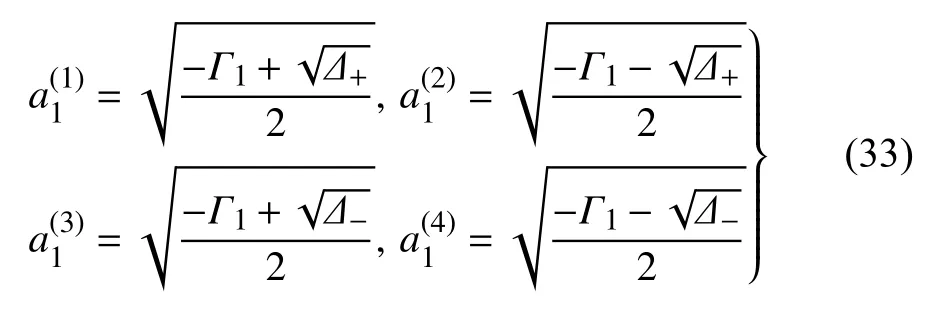
(2)Γ2±＜0

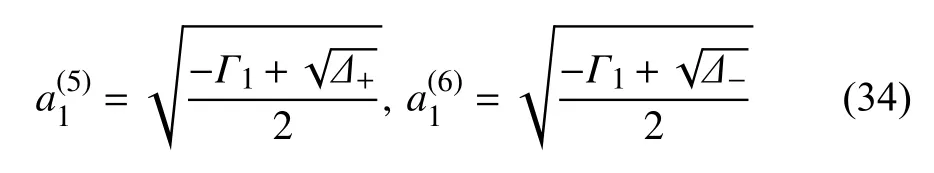
(3)Δ±＜0,系統無非零穩態解,此時系統只有零解.

根據穩態解幅值表達式(33)和式(34)可知,穩態解幅值是隨速度變化的函數.Δ±和 Γ2±也是隨速度變化的函數,于是不同的運行速度下,系統穩態解的數目可能也不相同.通常情況下,系統的非線性臨界速度Vn對應系統發生分岔時的速度,于是,通過求解系統發生分岔時的運行速度來判定系統的Vn.結合式(33)和式(34)可知,此時系統可能有多個分岔點,每一個分岔點對應的速度可能并不相同,即系統在不同的速度下均有可能發生分岔,通常系統發生分岔時的最小速度對應系統的Vn.基于此,下面對系統可能發生分岔的情況逐一討論.

(1)當 Δ±=0 時,系統發生分岔,此時對應系統的一個分岔速度,稱為第一分岔速度

(2)當 Γ2±=0 時,系統發生分岔,此時也對應系統的一個分岔速度,稱為第二分岔速度

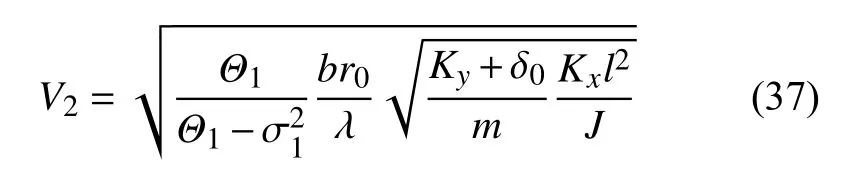
(3)當 Δ+=Δ-,并且系統滿足 Δ±＞0 時,此時對應系統的一個分岔速度,稱為第三分岔速度

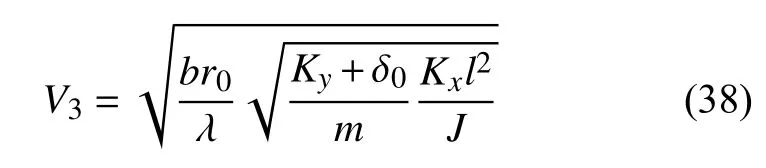
此時系統還需滿足

綜合上述分析,可判定系統的Vn為

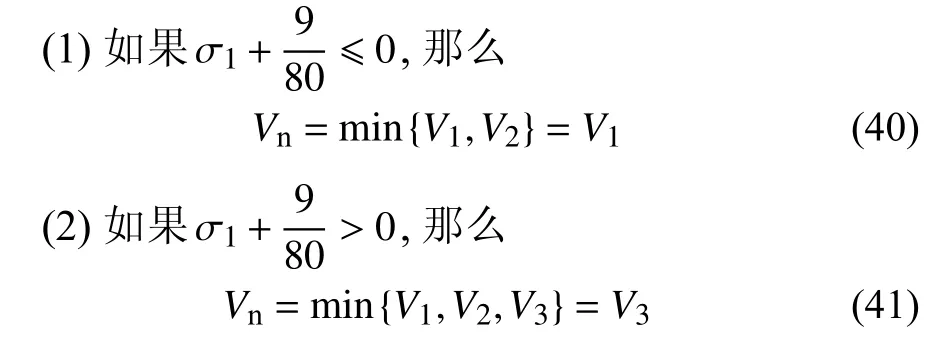
當求得系統穩態幅值a1后,代入式(27)～式(29)可求得a2,γ.對于求得的穩態解穩定性判定,可采用文獻[31]中的方法,為此設

式中a10,a20,γ0是系統的一組穩態解,它對應方程組(24)的奇點,即滿足式(25).δa1,δa2,δγ是疊加的小的攝動量.將式(42)代入方程組(24),并對δa1,δa2,δγ進行泰勒展開保留一次項,得到

此時系統穩態運動的穩定性依賴于式(43)右端的系數矩陣的特征值,右邊系數矩陣如下

式中

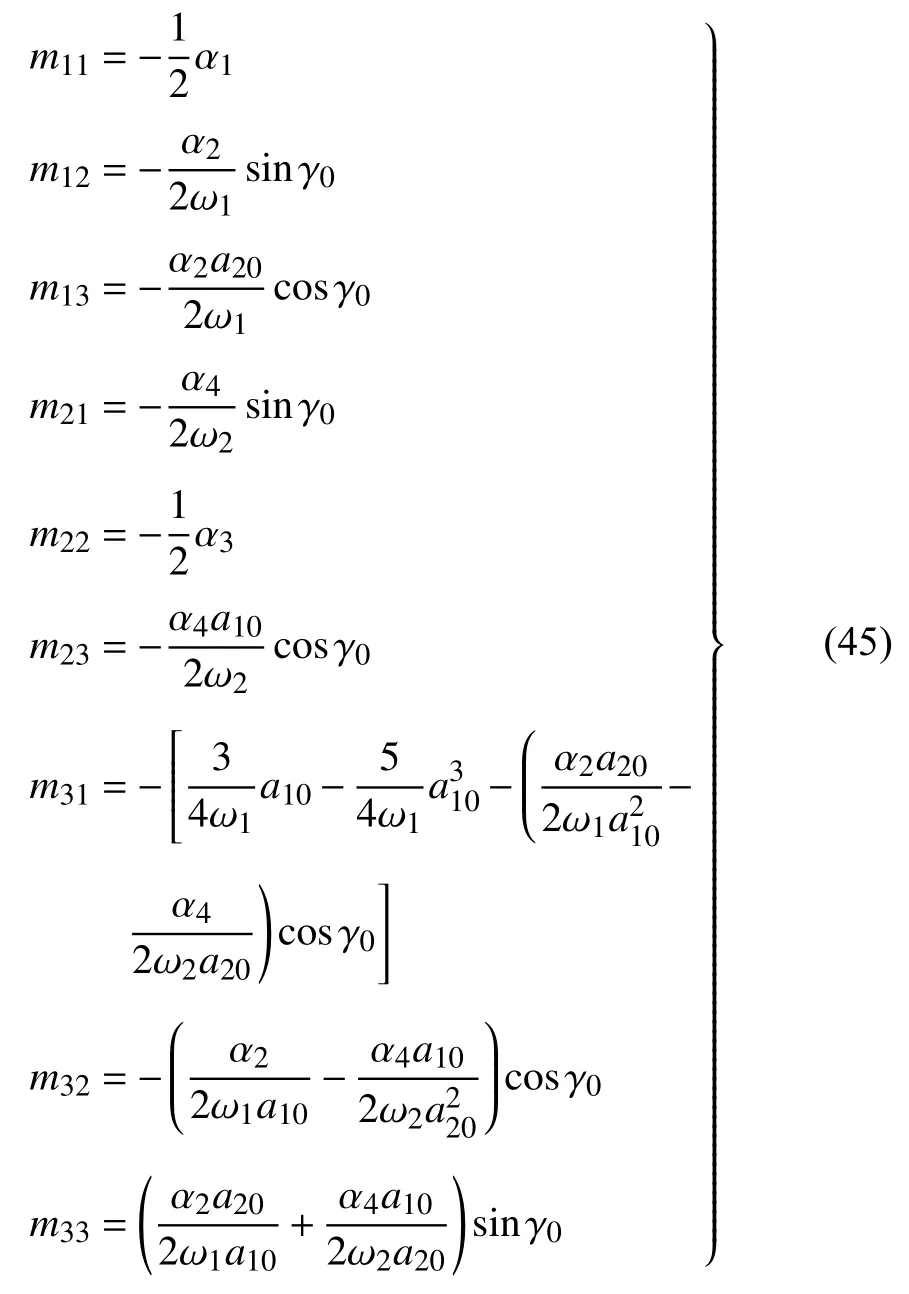
此時特征方程

對上式展開有

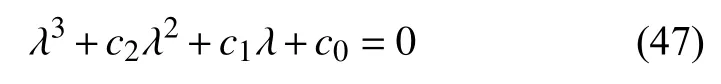
式中

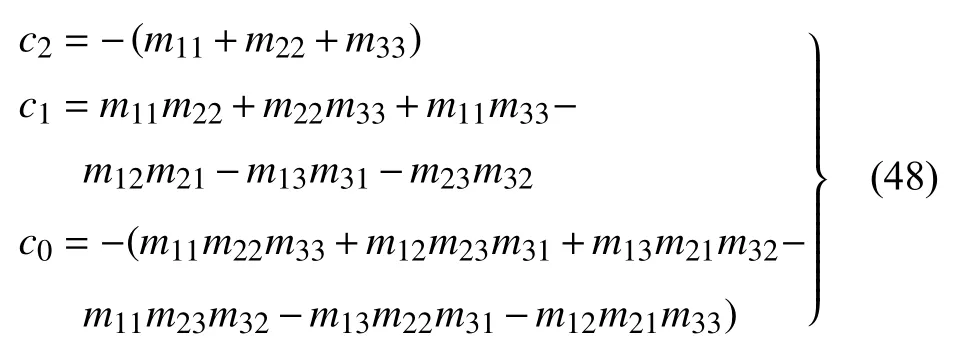
對于方程(47),采用卡爾達諾(Cardano)公式求解如下

式中

當式(49)～式(51)所對應所有特征值λi(i=1,2,3)的實部均為負數時,對應的穩態運動是穩定的,否則穩態運動不穩定.

將式(14)和式(17)代入式(10),結合式(23),可以得到穩態解的一次近似為

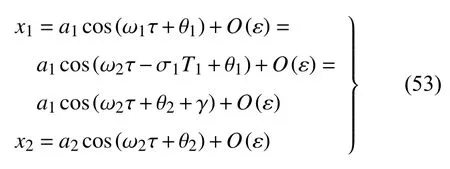
式中，a1,a2,γ均是常數,此時無量綱x1和x2以同一種頻率振動,當系統存在穩定的周期解時,系統的蛇行運動頻率fh

3 結果和討論

3.1 驗證

重新計算文獻[20]給出的輪對橫擺分岔圖的算例,并將本文結果與該文獻的結果進行了對比,如圖3所示.

圖3 中紅色三角符號代表文獻[20]中輪對橫擺幅值結果,藍色曲線是自編程序的計算結果,二者吻合很好.此外,在之前的研究[14-19]中,將自編程序計算結果和與已有文獻中的實驗結果和數值結果也進行了許多對比驗證.

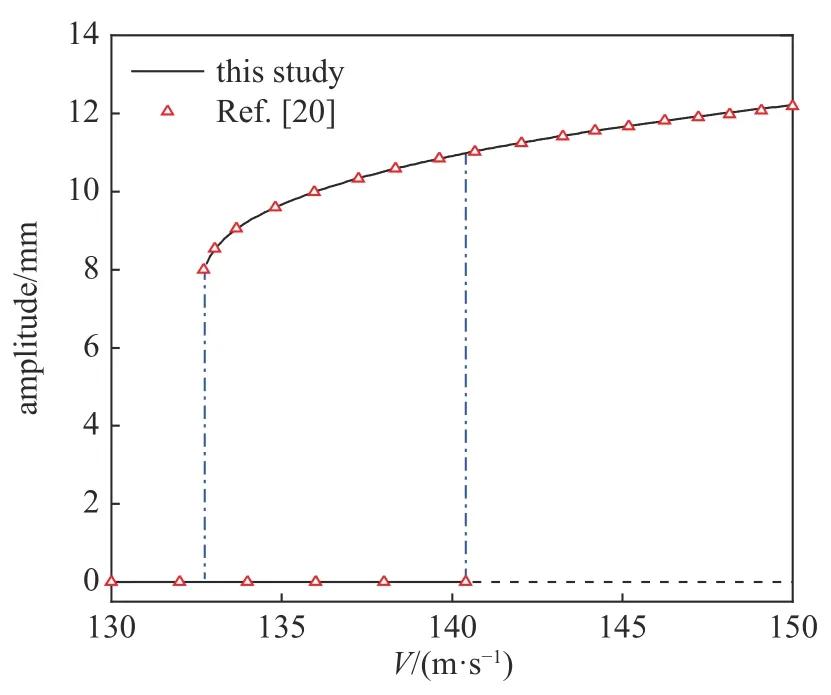
圖3 本研究結果與文獻[20]結果對比Fig.3 Comparison of results between this paper and Ref.[20]

接下來將數值計算結果和多尺度法的分析結果對比.數值計算采用四階變步長榮格-庫塔(Runge-Kutta,RK)法直接對方程(8)進行數值積分,略去瞬態部分得到x1和x2的時間歷程曲線如圖4(a)所示,圖4(b)是相軌跡在相平面上的投影.

由圖4 可知,此時x1和x2作周期運動,對其時間歷程曲線進行快速傅里葉變換(FFT)得到x1和x2的頻譜圖,如圖5 所示.

圖4 時間歷程曲線與相平面內相軌跡Fig.4 Time-history curves and phase trajectories in the phase plane

圖5 x1 和x2 的頻譜圖Fig.5 Frequency spectra of x1 and x2

由頻譜分析結合圖5 可知,此時x1和x2的頻率組成由基頻fh及fh的奇數倍頻組成.fh所對應的諧波分量幅值遠大于其他諧波分量幅值.x1和x2以相同的頻率fh作周期運動.此時數值計算得到的系統的蛇行運動頻率fh為0.152 00,而由本文解析公式(式(54))計算得到的fh為0.151 89,相對誤差僅0.07%.我們對x1和x2的時間歷程曲線進行濾波處理,得到相應的僅包含基頻fh的時間曲線如圖6 所示.

圖6 fh 對應的時間歷程曲線Fig.6 Time-history curves corresponding to fh

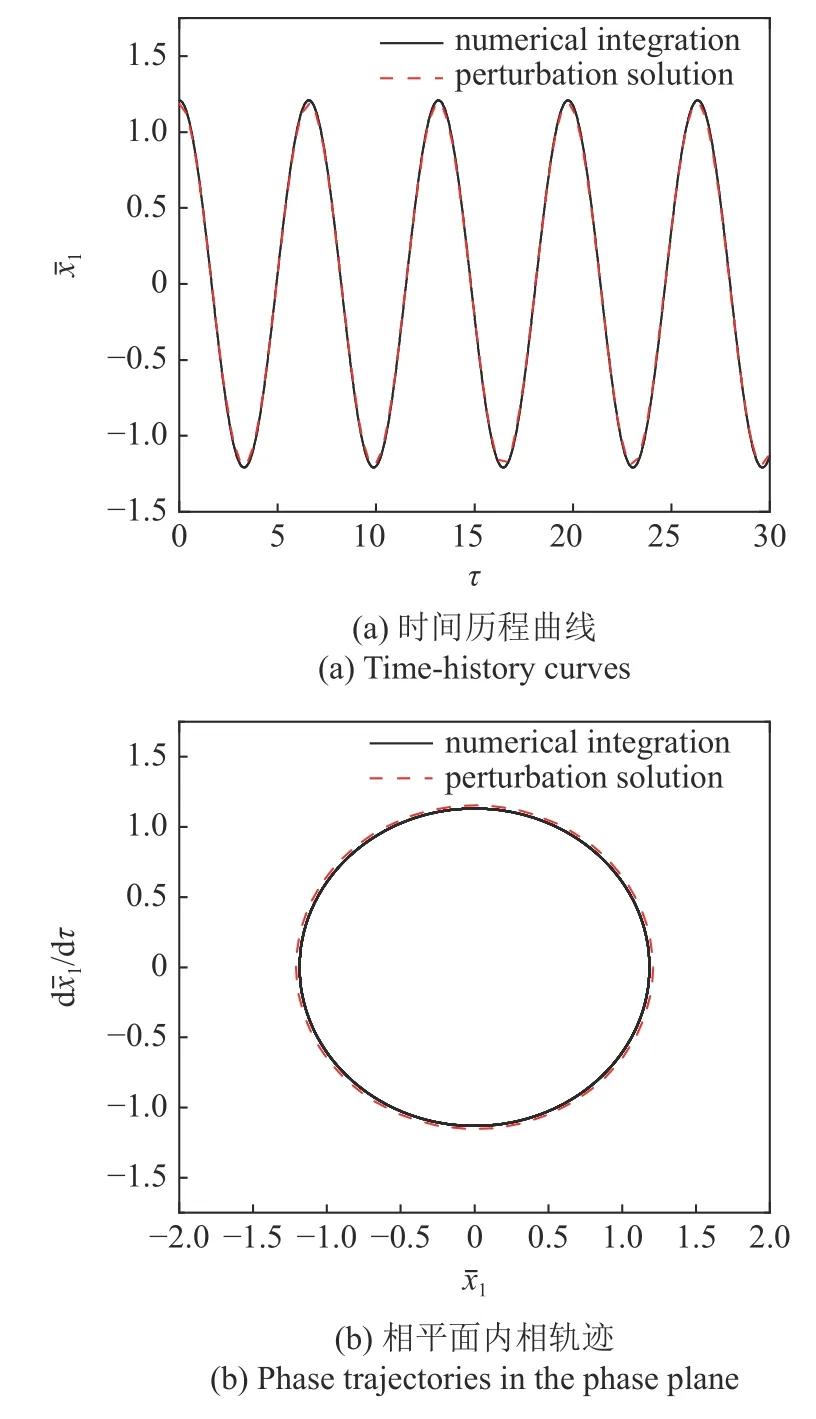
圖7 攝動解與數值積分結果對比Fig.7 Comparison between perturbation solution and numerical integration

圖8 給出了由本文解析式(27)、式(33)和式(34)計算的輪對橫擺和搖頭角分岔圖和數值結果的對比.圖8 中,實線代表穩定的穩態運動的幅值,虛線代表不穩定的穩態運動的幅值,數值積分不能求解出不穩定的穩態周期幅值.結合圖8 可以看出,由本文解析解(式(35)～式(38))計算的分岔速度中的線性臨界速度Vc約為204.7 m/s,由線性化系統系數矩陣特征值計算的Vc為207.1 m/s,相對誤差1.16%.因此,本文推導的解析解也能給出關于線性臨界速度的一個很好的近似.由本文解析式(35)～式(41)計算的非線性臨界速度Vn約為191.0 m/s,由降速法計算的Vn約為191.2 m/s,相對誤差約0.1%.系統的穩定的穩態周期幅值相對誤差不超過10%.

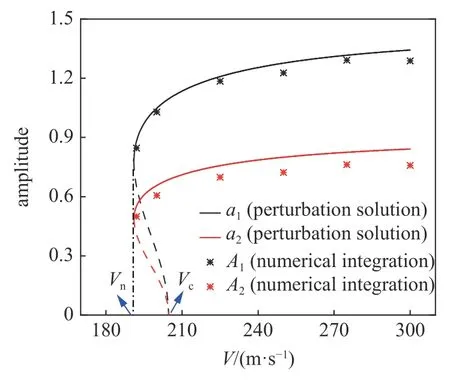
圖8 攝動解計算分岔圖和數值積分結果對比Fig.8 Comparison of bifurcation diagrams calculated by perturbation solution and numerical integration

通過以上解析公式的計算結果與數值結果的詳細對比,我們驗證了第2 章中基于多尺度法給出的一階解析解的正確性.

采用數值法計算輪對系統的非線性臨界速度通常需要大量的計算,例如,當采用降速法時:基于路徑跟蹤策略,首先通過增加運行速度使系統經過擾動后處于穩定的周期運動的狀態,即系統有穩定的極限環幅值,隨后逐步降低運行速度,在每一步中,當前速度下系統的最終穩態解對應的運動狀態作為后續下一個運行速度的初始值從而繼續計算,當初值問題的暫態解最終趨于平凡解時,計算結束.此時對應系統的一個分岔速度,通常為非線性臨界速度.計算的非線性臨界速度的精度取決速度離散化的步長,要獲得更加準確的臨界速度值,需要細化離散化的步長,導致時間成本增加.而通過非線性臨界速度的解析表達式,我們可以直接求解系統的非線性臨界速度,更重要的是,我們可以更加方便直接的進行參數對于系統非線性臨界速度的影響規律研究.

3.2 參數影響規律

根據非線性臨界速度的解析表達式(35)～式(41),很明顯,系統的V1,V2,V3與等效錐度λ的平方根成反比,從而系統的非線性臨界速度Vn與λ的平方根成反比.圖9 給出了由式(35)～式(41)確定的Vn隨λ的變化曲線.隨著λ的增加,Vn的減小速率逐漸減小.文獻[34]中給出,系統的線性臨界速度Vc與λ的平方根近似成反比,這說明λ對于Vc和Vn具有相同的影響規律.工程應用中,為提高車輛的運動穩定性,我們應該盡可能提高系統的Vc和Vn.于是在滿足其他設計要求的情況下,我們應該盡可能減小車輪踏面的等效錐度.

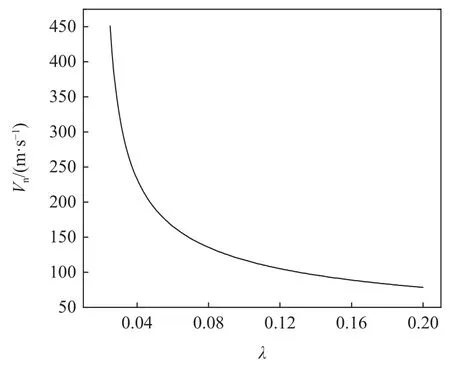
圖9 Vn 與λ 的關系曲線Fig.9 Relationship between the Vn with λ

接下來我們研究Vn隨一系縱向剛度Kx這一單一因素的變化規律,其他參數保持不變,如圖10 所示.

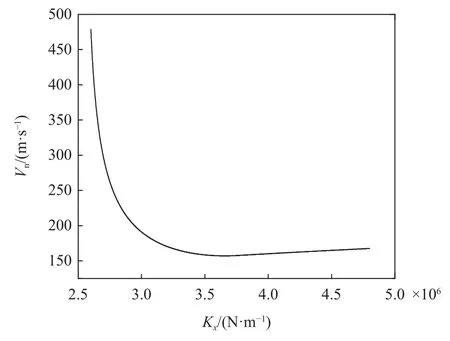
圖10 Vn 與Kx 的關系曲線Fig.10 Relationship between the Vn with Kx

當 σ1+=0 時,對應有

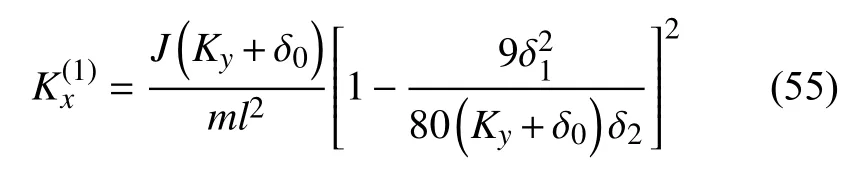
式中c1,c2,c3,c4均是常數.

式(56)中,當Kx＞=3.832 6 MN/m 時,Vn與Kx的四次方根成正比,是隨Kx增加而緩慢單調增的函數;而當Kx＜=3.832 6 MN/m 時,從上面表達式可以看出,Kx的四次方根之前的因子不再是常量,而是Kx的非線性函數,因而該式是一個具有極值的函數,我們可以求出其極值.在我們所關注的參數范圍內,求Vn解析表達式關于Kx的導數并令其等于零,化簡有

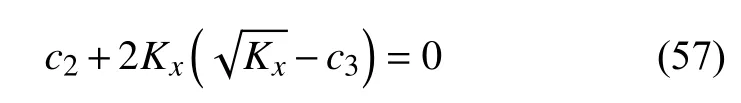
圖11 和12 給出由本文解析式(27)、式(33)和式(34)計算的無量綱橫擺和搖頭角分岔圖.

圖11 中,分別計算了一系縱向剛度Kx取2.9 MN/m,3.0 MN/m 和3.1 MN/m 時系統無量綱橫擺和搖頭角幅值隨速度V的變化曲線.結果表明,同一Kx值對應系統穩定的極限環幅值隨著V的增加而逐漸增大,當V越大,極限環幅值的增大速率越慢.同一V值,系統穩定的極限環幅值隨著Kx的增大而增大.

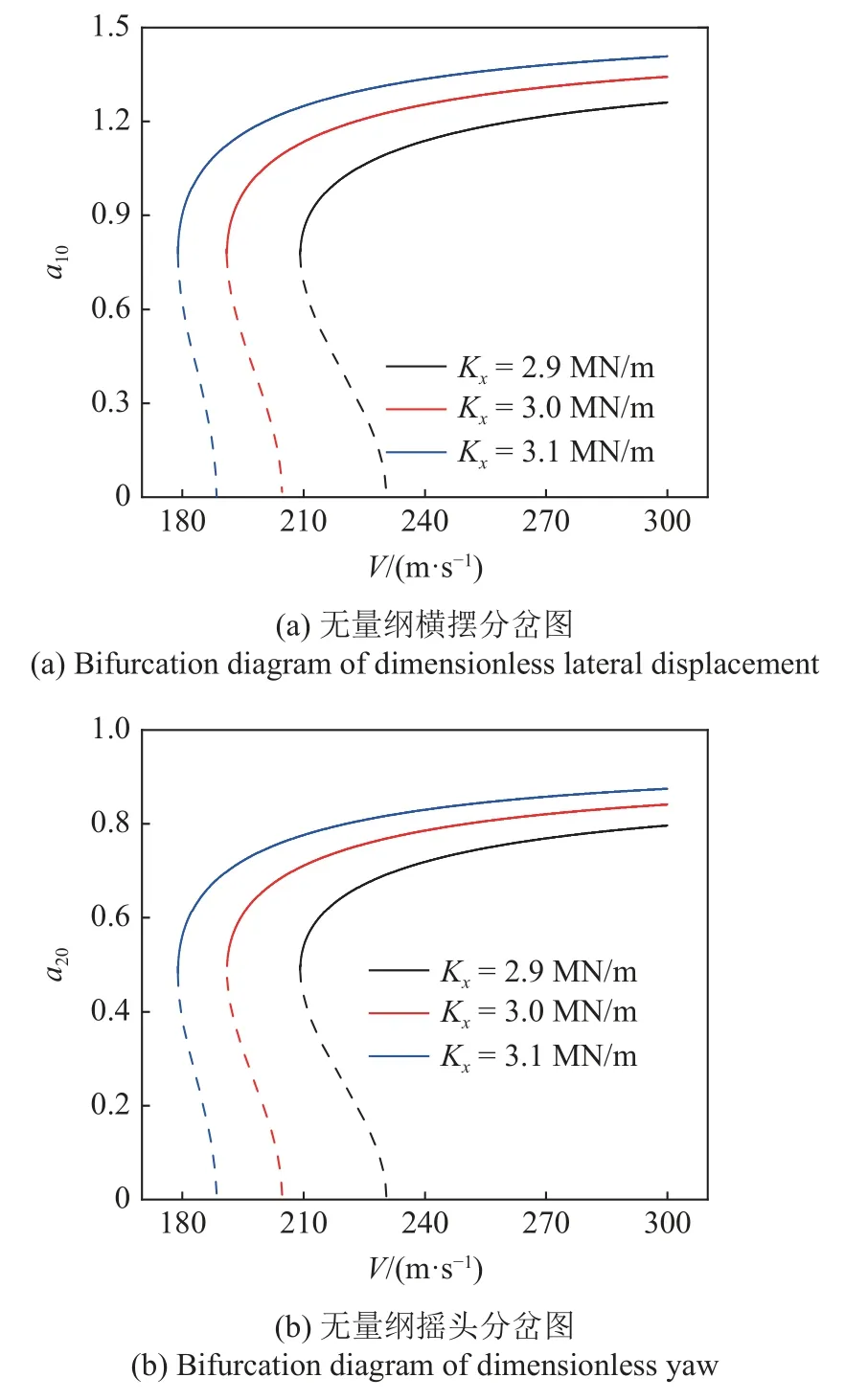
圖11 不同Kx 值對應系統的分岔圖Fig.11 Bifurcation diagram of the system with different Kx

圖12 中,分別計算了車輪踏面等效錐度λ取0.04,0.05 和0.06 時系統無量綱橫擺和搖頭角幅值隨速度V的變化曲線.結果表明,同一λ值對應系統穩定的極限環幅值隨著V的增加而逐漸增大,當V越大,極限環幅值的增大速率越慢.同一V值,系統穩定的極限環幅值隨著λ的增大而增大.

圖12 不同λ 值對應系統的分岔圖Fig.12 Bifurcation diagram of the system with different λ

一般情況下,根據Vn的表達式(35)～式(41),系統的許多其他參數均會對Vn有所影響,因此在設計轉向架參數時,應該對各種不同的參數組合方案進行比較,以期獲得最佳的參數匹配范圍.本文推導的解析表達式可以對系統參數的初期設計提供一定參考.在進行參數優化設計時,不需要采用數值方法對每一個參數組合進行大量微分方程組的積分計算,采用本文給出的解析表達式(35)～式(41)可以很快計算出每個參數組合對應的動力學性能指標,從而快速獲得最優參數組合.

4 結論

本文采用多尺度方法對車輛輪對系統動力學特性進行了解析求解.主要工作和結論如下.

(1)給出了系統的極限環幅值和非線性臨界速度的解析表達式.相比于數值解法,通過解析公式,我們可以直接給出系統的非線性臨界速度,更加方便地研究系統參數對于非線性臨界速度的影響規律.給出了一系縱向懸掛剛度和車輪踏面等效錐度對于系統分岔圖和非線性臨界速度的影響規律.

(2)在滿足其他設計要求的情況下,一系懸掛剛度對臨界速度影響較為復雜.在我們所研究的參數范圍內,系統非線性臨界速度隨一系縱向剛度的變化存在一個極小值.在剛度較低(極小值左側)時,臨界速度隨剛度減小而有較明顯增加,而當剛度較高(極小值右側)時,臨界速度會隨剛度增加緩慢增加.適當減小車輪踏面等效錐度有助于提升車輛系統的線性和非線性臨界速度,從而提升車輛運動穩定性.車輛系統發生蛇行失穩時的極限環幅值隨著一系縱向懸掛剛度和車輪踏面等效錐度的增加而有所增加.

(3)在轉向架結構設計與參數優化過程中,通過本文給出的解析表達式,可以很方便地計算出系統不同參數組合下的極限環幅值和非線性臨界速度,便于快速比較不同參數組合下的多種方案,從而篩選出最佳的參數匹配關系,為轉向架結構設計與參數優化提供參考.

附錄

附表 A1 輪對參數Table A1 Wheelset parameters